基于EMD和盒维数的Wigner-Ville分布交叉项的抑制方法

于兴林

（广东电网公司汕尾供电局，广东汕尾516600）

基于EMD和盒维数的Wigner-Ville分布交叉项的抑制方法

于兴林

（广东电网公司汕尾供电局，广东汕尾516600）

Wigner-Ville分布能够反映信号能量随时间和频率的变化趋势，但该分布易受到交叉项的干扰，限制了该方法的应用。通过分析复频信号Wigner-Ville分布的数学期望和Wigner-Ville谱图的特点，提出用均值阈值来抑制与真实频率不同的交叉项，用经验模态分解(EMD)和盒维数来抑制与真实频率相同的交叉项。仿真分析表明该方法较好地抑制了Wigner-Ville分布中的交叉项，同时该方法还具有良好的抗噪性。

【DOI】10.13616/j.cnki.gcjsysj.2016.09.022

1 引言

电力系统中的谐波、间谐波信号、低频振荡信号以及电压闪变信号均可表示为几个复频信号的叠加。准确地确定信号的频率和主导时间，有利于研究其产生的机理，有利于正确认识系统的本质。

对于这类信号可以用时间和频率的联合函数来表示信号频谱随时间的变化，如傅里叶分析法[1]、小波变换法[2]、Gabor变换法[3]等。傅里叶分析法只能处理平稳信号，后两者不能够反映非平稳信号的能量变化。Wigner-Ville可以反映非平稳信号的能量变化，但该分布受交叉项影响严重[4]。论文用信号的Wigner-Ville分布各频谱关于时间的期望和对含有信号项和交叉项的频谱随时间的变化进行经验模态分解（EMD）[5]，计算EMD分解出的各分量的盒维数[6]，通过设置盒维数阈值来滤除频谱中的交叉项，进而重构信号的Wigner-Ville分布，仿真分析表明该方法的有效性和准确性。

2 Wigner-Ville分布

Wigner-Ville(WVD)分布是一种Cohen类时频分布，当信号s(t)=ejw1t+ejw2t是2个复频信号叠加而成时，其WVD分布为：

式中，信号项W1(t,ω)=2π[δ（ω-ω1）+δ（ω-ω2）]；交叉项W2(t,ω)= 2πδ（ω-ωm）exp（ωdt）]。为频率的平均值，而ωd= ω1-ω2为频率之差。

如果一个信号由n个复频信号叠加而成，那么它的WVD分布就含有n个信号项和C2n个交叉项。随着复谐波数目的增加，交叉项的数目也会随之增加。

Ws(t,ω)关于时间的期望E(ω)如式（2）所示：

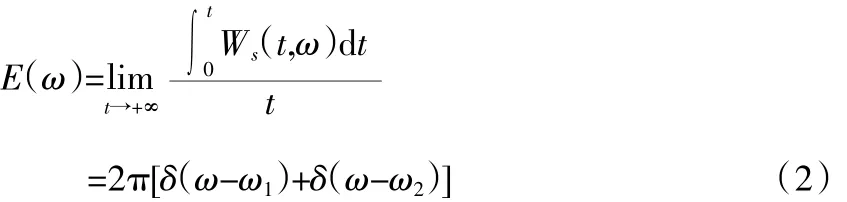
即Ws(t,ω)关于时间的期望E（ω）存在等于信号项的期望，交叉的期望为零。通过E（ω）可以滤除与真实频率不同的交叉项。若交叉项的频率与信号项的频率相同，则不能通过E（ω）来滤除交叉项。

3 EMD分解

EMD分解从原始信号中提取若干阶固有模态函数(IMF)，突出了原始信号的局部特征信息。IMF必须满足如下特点：

1）其极值点和过零点的数目应该相等或至多差1；

2）分别连接其局部极大值和局部极小值所形成的2条包络线的均值在任一点处为0。

设原始信号s(t)上下包络线的均值为m(t)，由s(t)减去m(t)得到c(t)，如果c(t)同时满足上述2个条件，则认为c(t)是从原信号中分解出的一个IMF分量。如果不满足条件，则对c(t)重复上述相同的过程直至满足条件为止，认为分解出了一个IMF分量。把原信号减去分解出的IMF分量，再对剩余量r(t)重复前述过程，直到r(t)成为一个单调函数时筛选结束。最终将原信号分解为一组振荡的IMF与一个剩余分量r(t)的和：

式中，ci(t)为原信号中各固有模态分量；r(t)为原信号中的剩余分量。

上述的完整过程称为原始信号的EMD分解。

4 盒维数

式中，yimax=max{yk(i-1)+1,yk(i-1)+2,…,yk(i-1)+k+1},yimin=min{yk(i-1)+1,yk(i-1)+2,…, yk(i-1)+k+1},i=1,2,…，N/k；k=1,2,…，M，M＜N，N为采样点数。

s(t)的网络计数N（kε）表达式为：

式中，N（kε）＞1。

在lg（kε）-lgN（kε）图中确定线性较好的一段为无标度区，设无标度区的起点和终点分别为k1、k2，则：

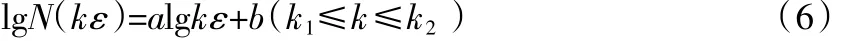
最后，可用最小二乘法确定该直线的斜率为：

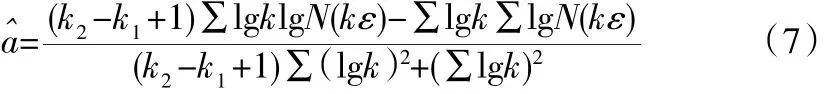
那么，盒维数DB为：

大量仿真表明：

1）采样频率相同，仿真时间为一个周期，离散正弦函数的盒维数随频率的增大而增大，其变化范围为1.079～1.5；

2）采样频率相同，频率不变，仿真时间取不同的周期，离散正弦函数的盒维数随采样时间的增大而成对数规律变化，趋近1.8；

3）采样频率相同，仿真时间相同，离散正弦函数的盒维数随衰减系数绝对值的增大而减小。

综合考虑滤除效果和仿真的实效，阈值取1.3。

5 实现步骤

1）求取原始信号的WVD分布Ws（t,ω）。

2）对Ws（t,ω）求取其时间序列上的期望E（ω），E（ωi）＜0.2max[E（ω）]ω1∈ω则Ws（t,ωi）为交叉项产生的，将其强制置零消除交叉项。否则为信号项或信号项与交叉项联合产生的，令si(t)=Ws（t,ωi），i=1，2，…，N。

3）分别对si(t)进行EMD分解即；

对各个IMF分量和剩余分量求取盒维数。将盒维数小于1.3的IMF分量和剩余分量叠加重构si(t)。

6 仿真分析

用Matalb构建仿真信号。

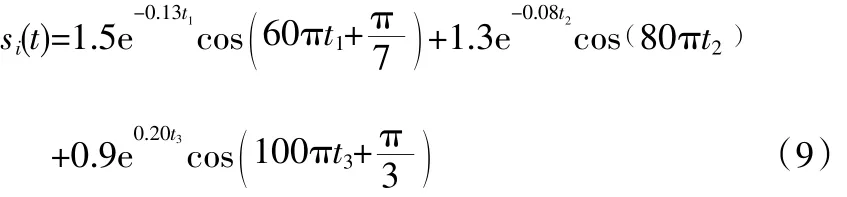
采样时间频率为100Hz，t1∈[0～0.59]s，t2∈(0.59～1.19]s，t3∈(1.19～1.79]s。在原始信号s(t)上叠加高斯白噪声，信噪比为12.32，并在s(t=0.4s)时叠加幅值为1.5的冲击噪声，将该含噪信号记为sn(t)；求取sn(t)的WVD分布，其WVD谱如图1所示。sn(t)的WVD谱中不仅受到交叉项干扰，也受到噪声的干扰，使sn(t)的WVD谱的频谱变宽，噪声背景的能量密度变大，从而使信号项的能量密度相对降低，不宜从噪声背景中辨别出来。对由频率相同的信号项和交叉项进行EMD分解并分别计算各IMF分量和剩余分量的盒维数。将盒维数小于1.3的分量相加重构WVD谱，从而降低交叉项的影响。重构信号的WVD谱如图2所示。对比图1和图2可以看出，含噪信号sn（t）的WVD谱图经过论文中的方法处理后，交叉项得到了消除，噪声干扰得到了抑制，信号项得到了加强。

图1 sn的WVD谱图及其投影图

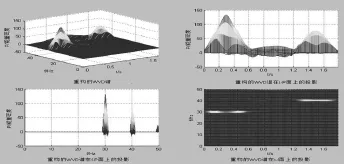
图2 sn重构的WVD谱图及其投影图

7 实例分析

采用实际电弧电流信号，采样频率为6400Hz，持续0.15s。实验中再加入的白噪声，信噪比为4，波形如图3所示。

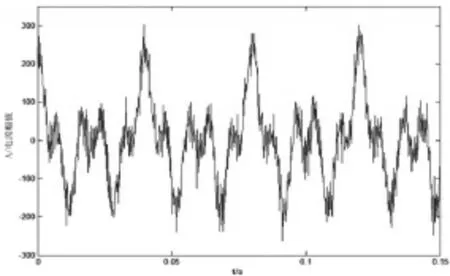
图3 原始电弧炉电流信号

利用论文中的方法直接对电弧炉电流含噪信号进行分析，结果如图4所示，可以看出，该方法可以有效地抑制交叉项，真实地反映信号的能量变化。

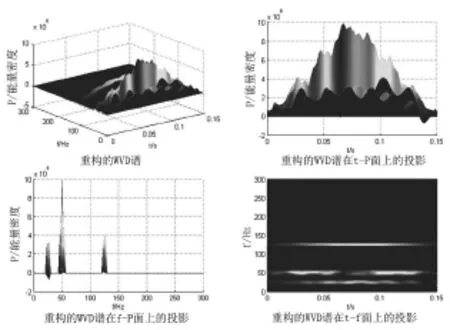
图4 电弧炉电流信号重构的WVD谱图及其投影图

8 结论

论文运用Wigner-Ville分布、EMD和盒维数来研究电力系统中的一类可以分解为有限个正弦信号相加的信号。通过对信号Wigner-Ville分布中各频谱随时间的变化进行EMD分解并计算分解后各分量的盒维数来抑制交叉项。较好地抑制了Wigner-Ville分布中的交叉项，同时该方法还具有良好的抗噪性。仿真分析表明了该方法的有效性。

【1】薛雪东，程旭德，徐兵，等.基于STFT的高压电气设备局放信号时频分析[J].高电压技术，2008（1）：70-72+141.

【2】栾某德，刘涤尘，廖清芬，等.基于改进小波系数奇异值分解和小波去噪的低频振荡时变模式辨识[J].电网技术，2012(6)：141-147.

【3】贺苏赣，朱旭东.基于离散Gabor变换和增量Wiener滤波器的冲击电压波形重构算法研究[J].电工技术学报，2006(4)：87-91.

【4】Wright P S.Short-time fourier transforms and wigner-ville distributions applied to the calibration of power frequency harmonic analyzers[J].IEEE Trans on Instrumentation and Measurement，1999，48(2)：475-478.

【5】韩松，何利铨，孙斌，等.基于希尔伯特-黄变换的电力系统低频振荡的非线性非平稳分析及其应用[J].电网技术，2008，32(4)：56-61.

【6】弓艳朋，刘有为，吴立新.采用分形和支持向量机的气体绝缘组合电器局部放电类型识别[J].电网技术，2011(3)：135-139.

Suppression Methods for Cross-term of Wigner-Ville Distribution Based on EMD and Box Dimension

YU Xing-lin
(Shanwei Power Supply Bureau of Guangdong Power Grid Corporation,Shanwei 516600,China)

Wigner-Ville distribution can reflect the signal energy trends overtime and frequency,but it is vulnerable to suffer cross-term interference,which limits the application of the method.By analyzing the mathematical expectation of the complex-frequency signal Wigner-Ville distribution and Wigner-Ville spectral characteristics,the paper proposes the mean threshold to suppress cross-term which is false frequency and the empirical mode decomposition(EMD)and box dimension to suppress cross-term which is true frequency.Simulation results show that the method can better suppress the cross-termin Wigner-Ville distribution,while the method also has good noise immunity.【关键词】复频信号；Wigner-Ville分布；经验模态分解；盒维数

the complex-frequency signal;Wigner-Ville distribution;EMD;box dimension

TN911.6

A

1007-9467（2016）09-0047-03

2016-07-11

于兴林(1987～)，男，河南南阳人，从事电力系统信号处理研究。