基于多目标约束的机车驾驶策略优化研究

王 烈，王 鹏，胡齐芽，张海洋

WANG Lie1, WANG Peng2, HU Qi-ya3, ZHANG Hai-yang3

（1.中国铁道科学研究院 运输及经济研究所，北京 100081；2.中国铁路总公司 运输局，北京 100844；3.中国科学院 计算数学与科学工程计算研究所，北京 100190）

(1.Transportation and Economics Research Institute， China Academy of Railway Sciences， Beijing 100081， China；2. Transportation Bureau， China Railway， Beijing 100844， China； 3.Institute of Computational Mathematics and Scientific/Engineering Computing， Chinese Academy of Sciences， Beijing 100190， China)

基于多目标约束的机车驾驶策略优化研究

王 烈1，王 鹏2，胡齐芽3，张海洋3

WANG Lie1, WANG Peng2, HU Qi-ya3, ZHANG Hai-yang3

（1.中国铁道科学研究院 运输及经济研究所，北京 100081；2.中国铁路总公司 运输局，北京 100844；3.中国科学院 计算数学与科学工程计算研究所，北京 100190）

(1.Transportation and Economics Research Institute， China Academy of Railway Sciences， Beijing 100081， China；2. Transportation Bureau， China Railway， Beijing 100844， China； 3.Institute of Computational Mathematics and Scientific/Engineering Computing， Chinese Academy of Sciences， Beijing 100190， China)

在概述国内外研究现状的基础上，分析影响机车牵引能耗的 4 类主要因素，提出机车驾驶策略优化研究即在满足安全、准点、舒适等多目标条件的约束下，寻找一条最优速度曲线，使列车由起点到达终点消耗的能量最少。将列车运行的全过程划分为平缓坡、上坡和下坡等多种运行状态的组合，通过建立基于多目标约束的能耗最优控制模型，提出不同阶段对应的机车驾驶策略，并通过实车验证该模型具有显著的节能效果。

铁路；机车能耗；驾驶策略；多目标约束

1　概述

1.1国内外研究现状

机车驾驶策略指机车乘务员在机车启停、运行等过程中所采取的不同操纵方式，如加减挡的时间、位置、达到目标速度及保持恒速所用时长等。目前，国内通常做法是根据经验判断或技术人员测试后制成相关操纵规程，机车乘务员依照列车运行监控记录装置 (LKJ) 及机车信号要求执行。随着我国铁路快速发展，高速动车组、大功率机车大量投入使用，机车能源消耗成为铁路运输能耗的主要环节。机车能耗受线路状况、机车型号、速度、重量等运行条件影响，通过建立模型可以将诸多因素进行量化分析，再经过不断优化计算，可以获得最佳的驾驶策略。该驾驶策略是在满足安全、准点、舒适等多目标运营条件的约束下，满足最低能耗要求的机车操纵方式。

满足安全、准时、舒适及限速等多目标要求的列车节能操纵是一个非线性有约束的动态最优化问题，国外学者主要采取经验总结、计算机仿真、数据统计、数学建模等方法，围绕列车节能进行研究。20 世纪 60 年代，美国开发列车牵引通用计算包 (Train Performance Calculator，TPC)，可以根据线路平纵断面和列车编组，计算列车运行时分，评价机车牵引性能[1]。20 世纪 80 年代以来，德国、澳大利亚、英国、俄罗斯等相继进行内燃机车优化操纵的研究和试验，其中前苏联铁路专家奥西波夫在《列车合理操纵和机车实验》专著中提出优化操纵方法对于提高列车运行效率及节约能耗方面的作用。20 世纪 90 年代以来，日本、韩国、丹麦、新加坡、加拿大、以色列、匈牙利、保加利亚等也加入列车节能运行研究，如日本交通控制实验室研制的铁路牵引计算和模拟系统 (UTRAS)，为列车牵引计算、运行控制、运营分析提供系统指导。2015 年，荷兰学者 Gerben 基于最优控制理论与算法构建节能运行模型 (Energy-efficient Operation or in Dutch ‘EnergieZuinigRijden’，EZR)，确定各车次运行最优速度目标值和惰行点，并且将能耗效率因素引入列车运行图的编制过程中，通过应用于乌得勒支—雷嫩的城际铁路表明，基于该模型编制的运行图能耗大幅降低[2]。

国内学者大多是根据我国铁路运营的特点开展列车节能研究，有的根据影响铁路机车牵引众多能耗因素进行探讨和分析，有的根据现场多年的实践操纵经验提出优化措施，有的在国外的研究成果及理论的基础上结合现代智能算法构建更为复杂的模型。国内主要机车节能驾驶策略优化算法如表 1所示。

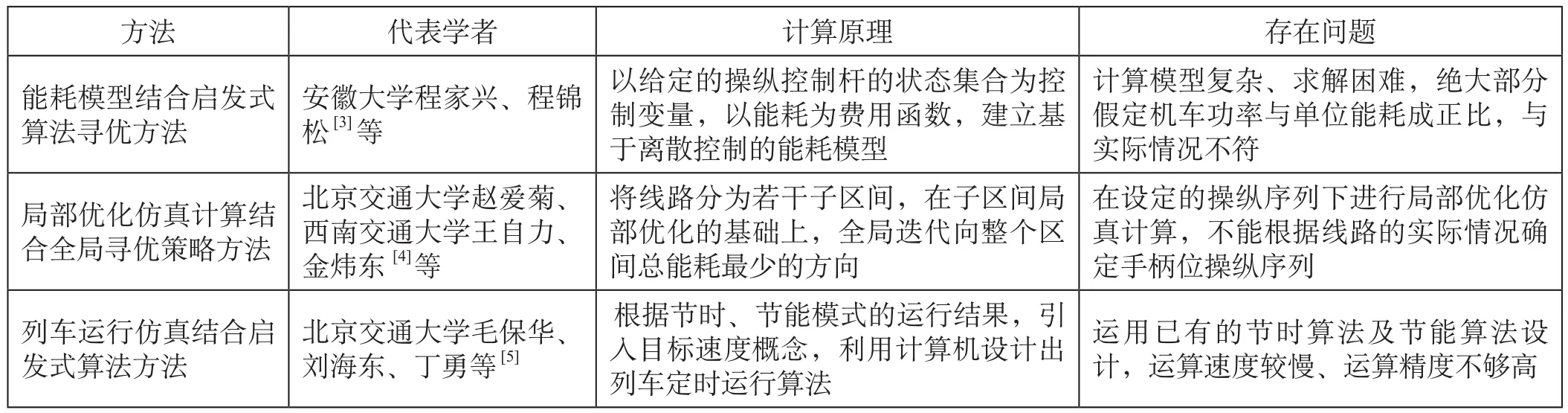
表1　国内主要机车节能驾驶策略优化算法

铁路机车能耗影响因素众多，根据设备、环境、管理和人员等要素主要分为移动设备、运输组织、运营环境、机车操纵 4 类[6]。其中，移动设备主要是指机车车辆属性，包括机车牵引特征、基本阻力特征、制动特征等；运输组织主要包括速度特性、临时限速、停站方案、运行时分等因素；运营环境主要指坡道、曲线、桥隧等线路属性，而自然环境如气候和海拔等也是影响机车能耗的重要因素；机车操纵指在列车的运行过程中司机的驾驶行为特征，不同的机车操纵方式对列车能耗具有不同影响。有经验的司机能够保证在满足运输需求的前提下，掌握较好的操纵时机，减少诸如接近限速时被迫使用制动减速、制动时机过早损失动能、惰行使用时机不当等造成的能源浪费。我国铁路规模大、里程长，不同地区或线路之间的运输情况各异，列车司机操纵水平不一，并且在进行操纵时存在一定的自主空间，牵引能耗仍然存在很大的节省空间。具体机车牵引能耗影响因素如图 1 所示。

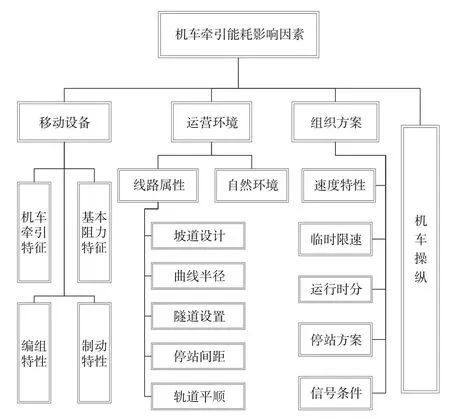
图1　具体机车牵引能耗影响因素

2　机车驾驶能耗最优控制算法

机车牵引过程一般由启动、恒速、惰行、制动等多个阶段或环节组成[7]。由于施工、线路状况、曲线半径等原因，列车在运行过程中还受到线路、道岔等设备允许速度的限制，不同等级列车面临的限速条件也不尽相同。每一阶段列车的受力情况、运行特征各有差异，在前述提到的诸如线路坡度、机车牵引制动特性、运行速度等多种因素的共同影响下，列车在不同阶段的能源消耗情况也不同。

从能耗优化的角度研究优化机车驾驶策略，可以理解为列车能耗最优控制问题，即在满足一定的约束条件下，寻找最优的速度曲线，使列车在规定的时间内由起点到达终点，消耗的能量最少。约束条件主要包括线路信息和列车信息 2 个部分。其中，线路信息包括坡度、距离和限速条件；列车信息包括阻力公式、最大牵引功率、最大制动力和自身重量。在实际运营组织过程中还需要考虑安全正点、平稳舒适等因素，因而还应在加减速过程中补充对横向加速度的约束，在恒速运行过程中综合考虑目标速度值和惰行时长，这些约束条件可以在模型仿真计算中进行设置，现仅对能耗最优控制理论模型提出算法要点。

假设列车由 A 开往 B 点，则列车消耗的能量为

列车在运行过程中满足以下状态方程。

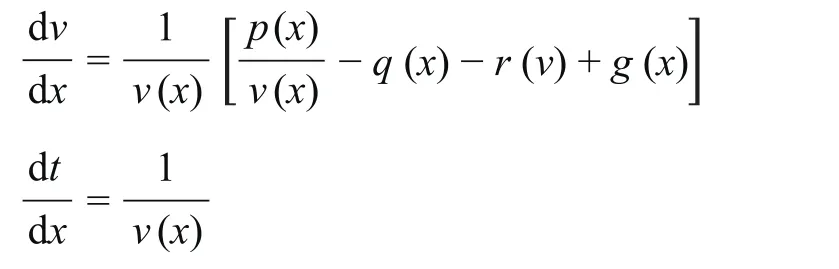
式中：x 为列车的当前位置即运行里程；v (x) 为列车在 x 处的速度；t (x) 为列车到达 x 处的时间；p (x) 为单位质量列车的牵引功率；q (x) 为单位质量列车的制动力；r (v) 为单位质量列车在速度为 v 时受到的阻力；g (x) 为单位质量列车的重力在斜坡方向上的分量。

公式 ⑵ 是由列车受力分析得到的动力学方程；公式 ⑶ 是关于速度、时间和距离的方程。其中，牵引功率 p (x) 和制动力 q (x) 为控制变量，通过调节 p (x) 和 q (x) 控制列车运行，p (x) 和 q (x) 分别满足 0≤p (x)≤P 和 0≤q (x)≤Q，其中 P 为单位质量列车的最大牵引功率，Q 是单位质量列车的最大制动力；速度 v (x) 和时间 t (x) 为状态变量，v (x) 满足 v (x)≥0，如果有限速条件，则还要满足v (x)≤V，其中 V 为最大限制速度。因此，列车能耗最优控制问题可以表述为

验证标准偏差相对稳定，具有统计意义。2004年QSAR国际会议正式形成经济合作与发展组织（英文简称OECD）规则，明确必须使用外部验证集（即测试集）来评价模型的预测能力。如果样本量足够大，也可以从105个样本中随机取8个样本作为测试集，97个样本作为训练集。本案例执行该规范。

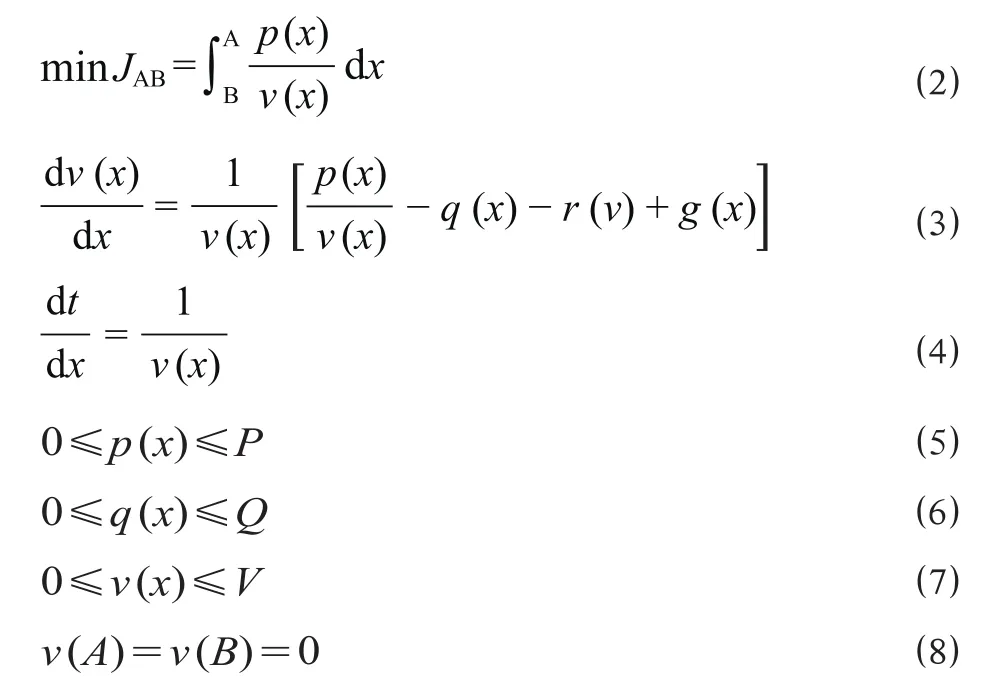
根据相关研究[8]，在工程项目管理中通过构造可以定量求解的最优控制理论模型，运用极大值原理能够有效地解决资源数量配置问题。因此，尝试运用极大值原理构建前述多目标约束的数学模型解决机车驾驶策略问题，首先定义哈密顿(Hamiltonian) 函数为

其中， α (x) 和 β (x) 为伴随变量，满足

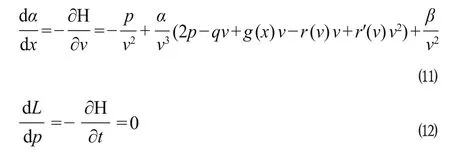
在满足 0≤p (x)≤P 和 0≤q (x)≤Q 的条件下，通过计算优化使 H 取得极大值。定义拉格朗日函数L = H + λ1p + λ2(P - p) + λ3q + λ4(Q - q)，其中 λ1、λ2、λ3和 λ4是非负的拉格朗日乘子。必要性条件为

通过推导和分析，得到列车能耗最优控制由伴随变量 α (x) 的 4 种状态组成，分别对应机车的最大牵引、匀速状态、最大制动和惰行 4 种不同运行状态，即

（1）α (x)＞v (x) 时，p (x) = P，q (x) = 0，即列车采用最大牵引功率牵引。

（2）α (x) = v (x) 时，p (x) ∈ (0，P)，q (x) = 0，p (x) ∈ (0，P)，q (x) = 0，此时列车采用部分功率牵引，使列车保持恒定速度运行。

（3）0＜α (x)＜v (x) 时，p (x) = 0，q (x) = 0，即列车采用惰行模式，牵引功率和制动力都为 0。

（4）α (x)＜0 时，p (x) = 0，q (x) = Q，即列车使用最大制动力刹车。

假设列车在匀速时保持的速度为 v0。引入 1 个新的辅助变量 θ (x) = α (x) / v (x)－1。当列车匀速行驶时，有 θ (x) = 0。在最大牵引、最大制动和惰行的时候，经过推导和计算可得

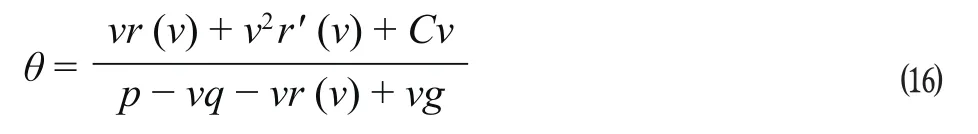
式中：C 是一个只依赖于 p (x)，q (x) 和 g (x) 的常数。通过推导得出，上坡时列车在 ξ 点开始最大功率加速，到达 η 点后速度变为 v0，此时 p (x) = P， q (x) = 0，；同理，下坡时 p (x) = 0， q (x) = 0，；而进站停车时，列车从 ξ 点开始惰行减速，此时 p (x) = 0，q (x) = 0，到达某一点 η 开始最大制动减速，此时 p (x) = 0，q (x) = Q，最佳转换点必要条件为 θ (ξ) = 0，θ (η) = －1。

3　实证分析

首先，定义列车上、下坡及平缓坡。在给定速度下，使用最大牵引功率牵引列车，列车的速度仍然下降，该坡道定义为上坡；在给定速度下，使用惰行牵引列车，即牵引功率和制动力都为 0，列车的速度仍然上升，该坡道定义为下坡；对于其他坡度较缓的坡道，均视为平缓坡。为了进一步验证优化驾驶曲线的应用情况，在某线进行试验，跟踪对比机车驾驶员使用驾驶优化曲线与否的耗电变化情况。以某 K 字头快速旅客列车为例，通过计算得到结果，牵引机型 SS8型，机车构造速度为 170 km/h，线路最高允许速度为 120 km/h，最大牵引功率为3 600 kW，机车自重为 88 t，机车的单位阻力公式为1.02 + 0.003 5 v + 0.000 426 v2，牵引总重为 1 005 t，25T 型旅客列车的单位阻力公式为 1.61 + 0.004 0 v + 0.000 187 v2。

（1）平缓坡情景。根据推导分析，处于平缓坡线路区间时，机车乘务员可采用部分功率 p (x) 牵引机车运行，即通过调整机车手柄级位以操纵机车，使列车保持恒定速度 V 运行，此时机车能耗最低。在实际操纵中，有时线路虽然坡度起伏变化不大但持续时间较长，如特大桥连续下坡道，司机一般会采用惰行一段时间减速再恢复加速的方式控车。经过理论计算和实车验证，平缓坡情景下司机以此种驾驶策略操纵机车的能耗较恒定速度控车的能耗更高，并且区间运行时分较长，在需要满足列车时刻表要求的条件下严重影响后续进站惰行制动节能策略的实施，因而全程能耗也更高。

（2）上坡情景。取距离信息为[0，1 800，2 500，3 100，4 000，6 000]，坡度信息为[3.8，6.7，5.4，6.2，2.3]。线路两端[0，1 800) 和(4 000，6 000] 为一般平坡，中间 [1 800，4 000] 属于上坡阶段。根据前面的推导和分析可知，列车应在某点 ξ ∈ [0，1 800) 开始加速，由匀速状态变为最大牵引状态，上坡结束后在点 η ∈ (4 000，6 000] 再由最大牵引状态变回匀速状态，，此时应满足 θ (ξ) =θ (η) = 0。最优开始加速点 ξ 是关于时间和能量耦合的函数的极小值，通过计算可知，当 ξ = 890 的时候，J 取得极小值。因此，在平坡路段 890 处开始加速时，机车在此上坡路段能耗最低。经过计算还可以得到，当 η = 4 247 时，θ (ξ) = θ (η) = 0。

假定列车不是在ξ= 890处开始加速，而是提前在 600m开始加速，或者滞后在 1200 m 处开始加速，同样画出相应的速度曲线和 θ 曲线，它们都不能满足在最大牵引状态结束时θ= 0。上坡情景速度曲线比较情况如图2所示。在图2中，实线表示上坡情景的最优速度曲线；上、下方虚线分别是在 600 m 处和 1200m 处开始加速所得到的速度曲线。上坡情景各速度曲线对应的θ曲线如图3所示。在图3中，实线是上坡情景最优速度曲线所对应的 θ 曲线；上、下方虚线分别表示在 600m处和1200 m 处开始加速所得到的速度曲线所对应的θ曲线，它们都不能满足在最大牵引状态结束的时候 θ = 0。

图2　上坡情景速度曲线比较情况

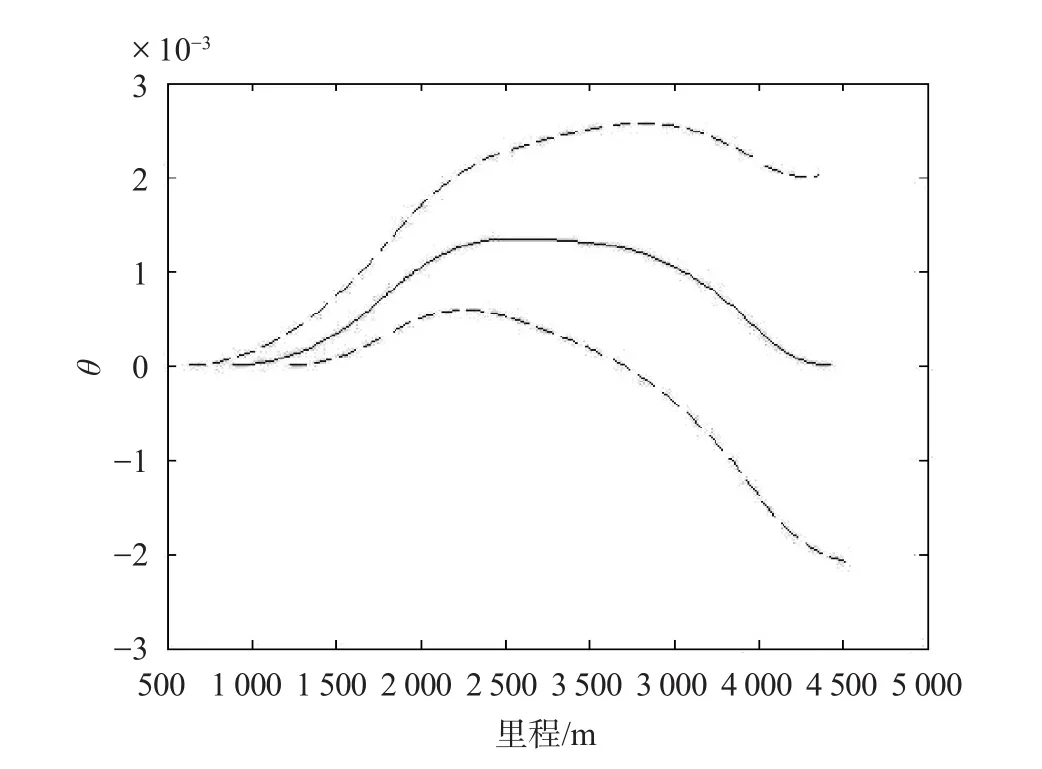
图3　上坡情景各速度曲线对应的 θ 曲线

（3）下坡情景。距离信息为[8 000，10 800，11 200，12 300，12 800，16 000]，坡度信息为[ -2.2，-6.1，-5.8，-6.4，-1.3]。线路两端 [8 000，10 800) 和 (12 800，16 000] 为一般平坡，中间 [10 800，12 800] 属于下坡阶段。根据前面的推导和分析可知，列车应在某点 ξ ∈ [8 000，10 800) 开始惰行减速，由匀速状态变为惰行状态，下坡结束后在点 η ∈ (12 800，16 000] 再由惰行状态变回匀速状态。。经过计算可知 ξ = 10 469 和η = 13 089 时，有 θ (ξ) = θ (η) = 0。假定列车不是在 ξ 处开始加速，而是提前或滞后开始惰行减速；同理，经过计算可知，它们都不能满足在惰行状态结束时 θ = 0。

根据理论计算和添乘记录，跟踪记录该线郑州—安阳间运用机车优化驾驶曲线的应用效果，如表 2 所示。通过表 2 可以看出，列车运行达到目标速度后，在具备条件的区间应用机车驾驶优化曲线指导司机操控机车，能够显著地降低机车在此区段内的能耗水平，各个区间电能消耗分别下降12.84%、5.42%、4.55% 和 10.26%，区间总能耗平均下降 7.97%。

4　结论

列车能耗最优控制即在满足一定的约束条件下，寻找最优速度曲线，使列车在规定的时间内由起点到达终点，同时消耗的能量最少。通过建立能耗最优控制模型，将列车在区间运行的全过程划分为上坡、下坡、平缓坡等过程组合，分别对应的列车运行状态为最大牵引、惰行、匀速和最大制动等情况，相应的机车驾驶策略如下。

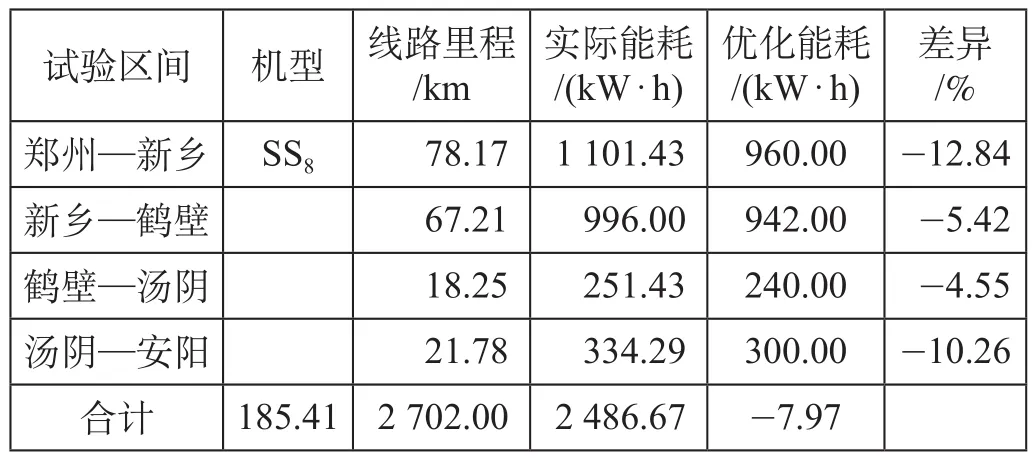
表2　郑州至安阳间能耗最优控制模型应用效果

（1）列车在起步之后，需要加速到目标速度V。这时应以最大牵引状态加速，迅速加速到需要的速度。

（2）列车在行驶过程中，在平缓坡路面应通过调节牵引功率，尽可能地保持匀速状态。

（3）列车在遇到上坡时，应在上坡之前提前加速，由匀速状态变为最大牵引状态。在上坡结束之后，当列车速度变回 V 时，应再次变回匀速状态。

（4）列车在遇到下坡时，应在下坡之前提前减速，由匀速状态变为惰行状态。在下坡结束之后，当列车速度变回 V 时，应再次变回匀速状态。

（5）列车在遇到限速条件变化等情况需要减速时，应尽可能使用惰行减速。

（6）列车在停车时，应先使用惰性减速，到达一定程度之后，再变为最大制动减速。

在机车不同手柄级位的转变过程中，该算法均能够精准地计算出运行里程，如开始加速的地点、开始惰行的地点和开始制动减速的地点，更便于司机操纵。通过实际应用，证明在具备条件的线路区间应用该机车驾驶优化曲线具有显著的节能效果。

[1] 周 锋. 动车组牵引计算建模及软件仿真[D]. 成都：西南交通大学，2007. ZHOU Feng. Computation of Train Traction and Simulation Software on CRH2 Electric Multiple Unit Railcarset[D]. Chengdu：Southwest Jiaotong University，2007.

[2] Scheepmaker G M，Goverde R M P. The Interplay between Energy-efficient Train Control and Scheduled Running Time Supplements[J]. Journal of Rail Transport Planning & Management，2015(10)：1-15.

[3] 程锦松. 一种解列车控制问题的新算法[J]. 微机发展，1999，9(4)：1-3. CHENG Jin-song. A New Algorithm for Solving Train Control Problem[J]. Microcomputer Development，1999，9(4)：1-3.

[4] 金炜东，王自力，李崇维，等. 列车节能操纵优化方法研究[J]. 铁道学报，1997，19(6)：58-62. JIN Wei-dong，WANG Zi-li，LI Chong-wei，et al. Study on Optimization Method of Train Operation for Saving Energy[J]. Journal of the China Railway Society，1997，19(6)：58-62.

[5] 丁 勇，毛保华，刘海东，等. 列车节能运行模拟系统的研究[J]. 北方交通大学学报，2004，28(2)：76-81. DING Yong，MAO Bao-hua，LIU Hai-dong，et al. Study on Train Movement Simulation for Saving Energy[J]. Journal of Northern Jiaotong University，2004，28(2)：76-81.

[6] 薛艳冰，马大炜，王 烈. 列车牵引能耗计算方法[J]. 中国铁道科学，2007，28(3)：84-86. XUE Yan-bing，MA Da-wei，WANG Lie. Calculation Method of Energy Consumption in Train Traction[J]. China Railway Science，2007，28(3)：84-86.

[7] 黄丽珍，王 昊，王 烈. 机车牵引能源消耗因素分析及计算模型研究[J]. 铁道运输与经济，2014，36(9)：88-92. HUANG Li-zhen，WANG Hao，WANG Lie. Analysis on Influence Factors of Locomotive Traction Energy Consumption and Study on Its Calculation Model[J]. Railway Transport and Economy，2014，36(9)：88-92.

[8] 乔剑锋，王长峰. 基于极大值原理的最优资源配置[J]. 北京邮电大学学报，2013，15(5)：73-77. QIAO Jian-feng，WANG Chang-feng. Optimal Resource Configuration based on Maximum Principle[J]. Journal of Beijing University of Posts and Telecommunications，2013，15(5)：73-77.

责任编辑：冯姗姗

Study on Optimization of Locomotive Driving Strategy based on Multi-objective Constraints

Based on summarizing study status in China and foreign countries, this paper analyzes 4 major factors influencing energy consumption of locomotive traction, and puts forward the study on optimization of locomotive driving strategy is to seek a optimum speed curve as to achieve minimum energy consumption of trains from departure to destination under satisfying the multi-objective constraints including safety, punctuality and comfort. The whole process of train operation is divided into multiple running states like gentle slope, upgrade and downgrade, through establishing the optimized control model of energy consumption based on multi-objective constraints, the paper puts forward corresponding locomotive driving strategies in different stages, and then, the energy-saving effect of the model is proved obvious through actual train example.

Railway; Energy Consumption of Locomotive; Driving Strategy; Multi-objective Constraints

1003-1421(2016)02-0087-06+3

B

U260.15

10.16668/j.cnki.issn.1003-1421.2016.02.18

2015-12-09

2015-12-29

中国铁路总公司基金项目 (2015F010)；中国铁道科学研究院基金项目 (2013YJ090)