归纳方法轻松解题

陈敏杰

归纳方法轻松解题

陈敏杰

1.等面积法

【例1】如图，等腰三角形的三边长分别为17㎝，17㎝，16㎝.求腰上的高CD.

【解析】作AE⊥BC于点E.∵AB=AC,AE⊥BC，∴AE平分BC，即BE=CE=8，在Rt△ABE中，由勾股定理得AE=∵△ABC的面积=

【点评】当几何图形中出现高（垂直、距离）的时候，可以考虑用等面积法解决问题，即利用图形面积的不同表达方式建立等式.

2.整体代入法

整体代入法是比较巧妙的方法，不纠结于细节，从整体出发体现大局观.有些题目看似缺少条件，可以设而不求，整体代入，往往可以达到事半功倍、减少运算的效果.

【例2】直角三角形周长为30cm，斜边长为13cm，求直角三角形的面积.

又∵（a+b）2=a2+2ab+b2，∴172=132+2ab，∴

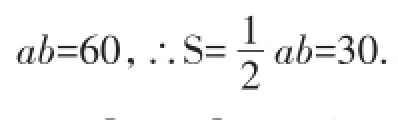
【点评】解答这类题时，部分同学常会感到题目似乎缺少条件，无从入手.关键是要把看似不好解决的问题当作已知条件整体代入到计算过程中，问题就能解决.

3.逆向思维法

从课本上，我们学到了一个定理：如三角形三边长a，b，c有下面的关系a2+b2=c2,那么这个三角形是直角三角形.这便是勾股定理的逆用．

【例3】如图所示的一块地，∠ADC=90°，AD=12m，CD=9m，AB=39m，BC=36m，求这块地的面积．

【点评】这是不规则图形，关键要添加辅助线化为规则图形，用规则图形相减求面积.△ACB不知道是不是直角三角形，这就要用到勾股定理的逆定理来判断它是不是直角三角形．

（作者单位：江苏省常州市武进区雪堰初级中学）