“解决问题的策略——一一列举”教学实录

◇张齐华

“解决问题的策略
——一一列举”教学实录

◇张齐华

一 课前探索，组内分享

（出示问题）

王大伯想用22根1米长的木条，围一个面积为20平方米的长方形花圃。如果22根木条要全部用完，而且不能折断，你觉得他能完成这一任务吗？

师：课前，同学们已经就这一问题进行过深入思考与探索，下面请大家先带着自己的作品和思考，在小组里交流一下各自的方法和结论。如果出现不同的见解，可以尝试进行讨论、协商，实在说服不了对方的，待会儿可以在全班范围内进行交流。

（学生小组交流，教师巡视并收集典型的解决问题方法和策略）

师：通过课前的研究，王大伯的任务能完成吗？

生：不能。

生：能。

师：看来，在能与不能上，大家还存在分歧。这样，觉得王大伯能完成这一任务的，带着作品和思考上来展示和汇报。

二 全班交流，建构策略

生：我觉得王大伯能完成任务。我帮他设计的是长方形，长5米、宽4米，剩下的4米可以放在一边。

（结合交流，他还展示了自己画的示意图。如图1）

图1

师：还有别的思路，也同样能帮助王大伯完成这一任务的吗？

生：我尝试了各种方法，发现都不行。后来我仔细研究了题目，发现里面并没有说不能靠墙。所以，我决定让这个长方形花圃一面靠墙，这样，它的长可以是20米，宽是1米，正好用去22根木条，而面积也正好是20平方米。

（结合交流，他也展示了自己所画的示意图。如图2）

图2

生：我的方法和他们都不一样。我觉得围一个花圃，四周至少需要1根木条竖在那儿作支撑，这样一来，22根木条只剩下18根。而18根木条正好可以围成一个长5米、宽4米的长方形，面积正好是20平方米。（出示图3）

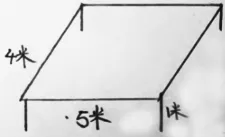
图3

师：看得出来，3个同学都特别想帮助王大伯解决这一问题。面对这3种方法，能否给出你们的评价？

生：我不太同意第一位同学的方法。因为题目中说得很清楚，22根木条都要用掉，不能有剩余。但他围成长方形后，还剩下4根木条，所以他的方法不符合题目的要求。

生：第二种方法，我也不赞成。因为题目中并没有说允许靠墙，而是说，就用22根木条围一个20平方米的长方形花圃。所以，一边靠墙是不合适的。

生：我也觉得不行。如果允许一边靠墙的话，那么，方法就不只是这一种，比如长10米、宽2米也能围出面积为20平方米的长方形花圃。

生：如果允许靠墙的话，那么，我们还可以靠两面墙、三面墙，这样的讨论就显得没有意义了。所以，我还是觉得，题目没有提示有没有墙，其实就是默认我们不能靠墙。

师：看来，大家对于第二位同学的方法，基本也是持否定的观点。那么，第三种方法呢？

生：我觉得，他的这种方法，有点儿像脑筋急转弯。我们都在思考，怎么用木条围一个长方形，他竟然让木条竖了起来。

生：我觉得他的这种方法很有创意，但有一个问题，既然可以在4个角落里各竖1根木条，那我们也可以在别的地方继续竖一些。这样，符合要求的情况也就越来越多，这个问题也就失去讨论的意义了。所以，我还是不太赞成让木条竖起来。

师：不管怎么说，这三个同学都在想尽一切办法帮助王大伯解决问题。只是解决问题时，有些方式不太被大家接受。这样，如果我们将问题表述得更清楚：就用22根木条平着围一个长方形花圃，不能剩余、不许折断，也不借助其他任何条件，能够围出面积是20平方米的长方形花圃吗？

生：不能！

师：我们都知道，22根木条可以围出多种不同的长方形，为什么你们觉得不能？能否展示出你们的研究和思考过程？特别提醒一下，接下来的时间里，每一位同学展示完毕后，台下的同学可以就着他的作品和思考，给出你的评价和建议。

生：我试了一下，如果长是7米，那么宽就得4米，但这个长方形的面积是28平方米，不符合问题的要求。所以我觉得王大伯的要求不可能实现。（如图4）

图4

生：我反对。虽然我也觉得这个任务不能实现，但你只举了一个例子是不能说明问题的，因为周长22米的长方形有好几种，万一另外有一种长方形的面积正好是20平方米呢？

师：能给大家展示一下你的作品吗？

生：我先用22除以2，发现这个长方形的长与宽的和是11米。然后，我想办法把11分成两个数的和，发现只有这样5种分法，但这5种分法，得出的长方形面积都不是20平方米。所以，我认为王大伯的任务没法实现。（如图 5）

图5

生：我的方法和他的很相似，只不过我是列表的（如图6）。通过列表，我也发现周长是22米的长方形有5种情况，但每一种长方形的面积都不是20平方米。所以，我也觉得王大伯的任务不可能完成。

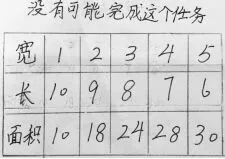
图6

师：两种方法看似不同，但仔细观察一下，有没有发现什么相似之处？

生：我发现他们举例时都很有顺序，比如长方形的宽，从1一直列举到5，一个比一个大，而长方形的长从10一直列举到6，一个比一个小。

生：我觉得按这样的顺序列举，有一个好处就是不容易遗漏。如果不按顺序列举，弄不好就会漏掉某一种情况。

师：说得真好！看来，列举时，我们要按一定的顺序进行。不过，我有一个疑惑，干吗非要把所有情况都列举出来，列举两三种情况，不就能说明问题了吗？

生：不行。因为题目问：王大伯的任务能实现吗？既然你要说明不能完成，你就得把所有情况都列举出来，并且一个一个验证。只有这样，我们才能说明王大伯的任务不能完成。如果你漏掉一个，万一这种情况正好是符合要求的，那就麻烦了。

师：看来，为了解决问题的需要，我们在列举时，不仅要按顺序，而且得把所有情况都列举出来，这在数学上就叫一一列举。（板书：有序、一一列举）还有没有不同的方法需要展示的？

生：我也是一一列举的，但我是根据面积来列举的。我发现，面积是20平方米的长方形，只有3种情况（如图7）。而通过计算，我发现它们的周长都不可能是22米，所以，王大伯的任务不可能完成。

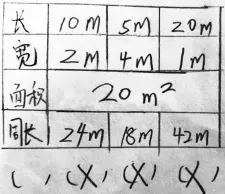
图7

生：我先对他的作品提一点儿建议。我觉得他在列举时没有按一定的顺序，所以有点儿乱，如果把长20米的长方形放在第一个，这样看起来更清楚。另外，我也是从面积角度思考的，只是我没有列表，而是直接画图的。（如图8）通过画图，我也发现面积是20平方米的长方形，周长不可能是22米，所以，王大伯的任务不可能完成。

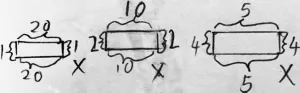
图8

师：看来，同样是一一列举，列表、画图和列算式都是可以的。老师这儿也带来了一个同学列举的情况（如图9），但结果和你们略有不同。谁来评价一下？

图9

生：我觉得他列举时重复了。比如这里的③号和④号长方形，一个长5米、宽4米，另一个长4米、宽5米，其实这两个长方形是一样的，只不过方向不同而已。所以，我觉得他列举的前面3种可以去掉，只留后面3种就可以了。

师：通过他的列举，你又有什么新的发现？

生：列举时不仅要有序、不遗漏，同时也要做到不重复。

生：也就是说，一一列举时，要把所有符合条件的长方形一个不多、一个不少地一一列举出来，这才是最好的。

三 深入观察，发现规律

师：通过刚才的学习，我们发现，一一列举是解决问题时一种有效的策略。正是借助一一列举的策略，我们发现王大伯的这一任务是没法完成的。不过，仔细看一下同学们解决问题时所列的表格（如图6和图7），一个是周长确定、面积在变化，另一个是面积确定、周长在变化。仔细观察表格中长、宽、周长和面积的变化，你有没有什么新的发现？

生：我发现，当长方形的周长不变时，长和宽离得越远，面积越小；长和宽越接近，面积越大。比如图6中，从前往后，长和宽的距离越来越接近，而它们的面积就越来越大。反过来看，也是一样的。

师：有没有发现，列举有序时，我们还很容易从中发现一些有趣的规律？

生：我发现，当长方形的面积不变时，长和宽的大小越接近，周长就越小；长和宽的大小相差越远，周长就越大。

师：不过，这两条规律适用于所有的长方形吗？如果让你继续来研究，你会怎么研究？

生：我会继续找一些长方形，让它们周长相等，然后看看它们的面积会怎么变；再找一些长方形，让它们面积相等，看看它们的周长又会怎样变化。

师：下面的时间，就请大家自己确定数据，验证一下这一规律是否也适用于别的长方形。

（学生小组内进行研究与验证，汇报略）

四 实践拓展，应用策略

师：这儿还有两个问题，你能尝试着用今天所学的策略进行思考吗？

出示问题如下：

1.一张靶纸共三圈，投中内圈得10分，投中中圈得8分，投中外圈得6分。小林投中了2次，他可能得多少分？（如图10）

图10

2.两枚硬币同时抛起，落地后，会出现几种不同的情况？

（学生尝试解决问题，随后全班交流对话）

师：通过研究，你觉得小林最终的总分可能有几种情况？

生：一共有10种情况（如图11），2次都投中的有6种，只投中1次的有3种，2次都没投中的有 1 种，6+3+1=10（种）。

图11

生：我觉得不对，题目中明明说了投中2次，所以，后面的4种根本不需要讨论。如果把“小林投中了2次”改为“小林投了2次”，那么答案就是10种。

生：我觉得也不应该是6种，而是5种。大家看，10+6=16，8+8=16，两次的总分是一样的，所以可以看作是同一种结果。

师：看来，在解决这样的问题时，一方面，我们要审清题意，不能粗心大意；另一方面，在进行一一列举时，我们还要根据问题的要求，不能重复、也不能遗漏。

生：第二个问题，我觉得一共有3种情况，分别是正正、反反和一正一反。

生：我反对，我觉得应该有4种情况，分别是正正、反反、正反和反正。

面对究竟是3种情况还是4种情况，学生展开了激烈的争论。最终，教师给出了如下建议：

建议1：给两枚硬币分别标上号码，一枚是1号硬币，另一枚是2号硬币。

建议2：试着用两枚硬币实际抛一抛，看看最终出现的到底是几种情况。

生：通过研究，我们发现，一正一反应该包含两种情况。我们给硬币标上号码后，发现实际上会出现这样4种情况：1号正面和2号正面、1号正面和2号反面、1号反面和2号正面、1号反面和2号反面。没有标号码时，我们还以为一正一反就是一种情况。一标上号码，我们才发现原来它们是不一样的。

师：以后在一一列举时，如果出现问题，有时，实验也不失为一种好的策略，它可以让我们对问题的思考更清晰、更准确。

（作者单位：江苏南京市北京东路小学）