基于狄洛尼三角网的等高线及挖填方分析研究
周浩,蔡欢
(天津市测绘院,天津 300381)
基于狄洛尼三角网的等高线及挖填方分析研究
周浩∗,蔡欢
(天津市测绘院,天津 300381)
基于对外业测量数据三维表达的目的,采用改进的逐点插入法构建狄洛尼(Delaunay)三角网,并结合Auto-CAD Civil 3D进行测量数据三维展示,实现了三维环境中等高线的绘制以及挖填方土方量的计算,可以较好拟合地形等高线起伏,直观分析挖填方的位置和土方量,使AutoCAD的应用由传统的二维模式向三维模式转变。
狄洛尼三角网;等高线;土方计算
1 引 言
数字地形模型(DTM)是对地表形态及属性信息的数学表达,包含空间坐标属性及地形属性特征。当其地形属性为高程值时,又被称为数字高程模型(DEM)。DTM主要有三种模型:等高线模型、规则格网模型和不规则三角网模型。等高线模型能比较直接地反映地形地貌,但不适合进行坡度计算、挖填方计算等地学计算。规则格网模型在GIS应用中很有利,但其数据量大,且需要分布较为规则的高程点数据的特点,难以表达复杂地形地貌。在大比例尺地形图的生产中,传统野外测量方法获取到的高程信息大多是不规则的离散点,一般采用不规则三角网(TIN)来表示其地形地貌变化[1]。在所有三角网生成方法中,狄洛尼三角剖分不仅能保证三角网的唯一性,而且能尽可能地避免狭长三角形的出现,是生成TIN的最好方法。
狄洛尼三角网具有以下三个性质:
(1)空外接圆性质:三角网中每个三角形的外接圆都不包含点集中的其余点。
(2)最大最小角度性质:在所有可能生成的三角网中,各三角形最小角之和最大。
(3)唯一性:无论从何点开始构造三角网,最终生成的狄洛尼三角网相同。
2 逐点插入法构造狄洛尼三角网
2.1狄洛尼三角网生成算法
狄洛尼三角网生成算法主要包括三类:逐点插入算法、三角网生长算法、分割合并算法。经试验发现:分割合并算法对复杂分布的离散点处理效果不理想,当相邻子三角网的形状都很不规则时,合并后的三角网极有可能出现不合理的凹陷部分。三角网生长算法则需要对每个新生成的三角形的三条边分别进行循环扩展,同时剔除重复三角形,直到没有新的三角形生成[2]。该方法算法简单,但是算法效率极低。所以本文采用改进后的逐点插入法来生成狄洛尼三角网,其算法思想是:
(1)剔除重复点。
(2)生成一个包含所有离散点的超级三角形。
(3)循环点集中的每个点:求出当前离散点落在哪些已有三角形的外接圆内,获取在这些三角形中只出现过一次的边,将这些边与当前点组成新的三角形,并删除受影响的三角形。
(4)将包含超级三角形顶点的三角形删除。
2.2三角形类
三角形类的主要作用包括:存储该三角形的三个顶点坐标;判断一个点是否是该三角形顶点;计算三角形面积、重心、外接圆圆心及半径。


2.3三角形边类
三角形边类的主要作用是存储边的两个顶点以及判断两条边是否重合。

3 狄洛尼三角网的应用
传统的二维平面对地形地貌的表现能力不足,体现为美观性和易读性较差。不规则三角网模型(TIN)的结构逻辑性强,数据量适中,利于进行坡度、坡向分析以及挖填方等地学计算。因此本文采用AutoCAD Civil 3D作为底层平台,实现基于狄洛尼三角网的等高线绘制和挖填方计算两个方面的应用。
3.1绘制等高线
等高线用来展示地形地貌特征。在三角网中通过内插方式生成等高线,以三维的方式绘制地表等高线分布,可以直观的表现地面的起伏状况,流程如下:
(1)遍历三角网中的每一个三角形,根据当前高程CurElev和三角形顶点坐标,计算三角形三边上的等值点。如果该三角形边上等值点的数量大于1个,则将这些等值点放入一个点集合CurPoints,再将这个点集合放入点集合链表AllPoints中。
(2)如果AllPoints中点集合总数大于0,则从All-Points中取出第一个点集合,作为新等高线的点集合LinePoints,否则退出。
(3)遍历AllPoints中的点集合,将点集合中的点和LinePoints中的第一个点或最后一个点做比较。如果相等,则将点集合中的其他点加入LinePoints头部或者尾部,并将点集合从AllPoints中移除。
(4)当AllPoints点集合中的所有点都不与Line-Points中第一个点或最后一个点相等时,表明当前等高线已经生成完毕。返回执行第2步直至AllPoints遍历完毕。
(5)利用AutoCAD Civil 3D将LinePoints点集合进行绘制,生成三维等高线图,如图1所示。
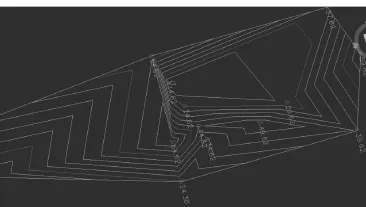
图1 三维等高线图
3.2DTM法挖填方计算
在建设施工项目中土方量计算是一项十分重要工作,关系到项目各方的切身利益。区域内挖填方的计算方法包括等高线法、DTM法、断面法以及方格网法,每种方法有不同的使用范围[3]。DTM法挖填方计算的原理是三角棱柱体积法,通过计算范围线内每个三角形区域的挖填方量,最终得到整个区域的挖填方总量[4]。计算流程如下:
(1)根据高程点集和选取的闭合范围线,得到计算区域的三角网。通过构造狄洛尼三角网得出需要计算的三角形。
(2)计算每个三角形的挖填方量。根据三角形挖填高度的不同,其挖填方计算方式分为两种:全挖或全填或有挖有填。
3.2.1全挖/全填
此时挖填部分是一个标准的三角棱柱体,如图2所示,其体积计算公式:

式中:S为三角形在XY平面上的投影面积,利用海伦公式计算;H1、H2、H3是三角形各顶点的挖填高度(取绝对值)。3.2.2 有挖有填

图2 全挖或全填
零线将三角形分成两个部分,根据零线与三角形的相交关系,存在两种分割情况:①零线经过三角线的一个顶点,与对边相交,形成两个底面为三角形的锥体;②零线与三角形两条边内部相交,分别计算锥体和楔体的体积。零线与三角形两条边内部相交,形成一个底面为三角形的锥体和一个底面为四边形的楔体。
①零线经过三角形的一个顶点,形成的两个底面为三角形的锥体,可以看做是两个三棱锥,如图3所示,其体积计算公式:

式中:S是锥体在XY平面的投影面积;H3是锥体顶点的挖填高度(取绝对值)。
锥体部分的体积计算公式:
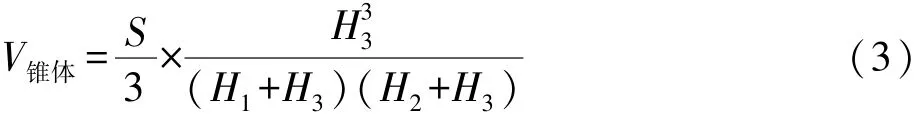
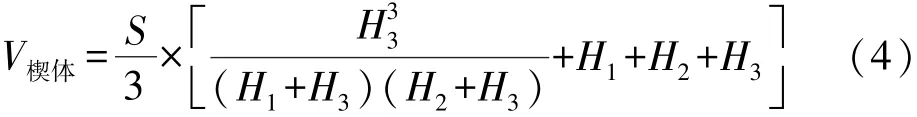
式中:S为三角形在XY平面的投影面积;H1、H2、H3为三角形各顶点的挖填高度(取绝对值),其中H3为锥体顶点的挖填高度,如图4所示。
楔体部分的体积计算公式:
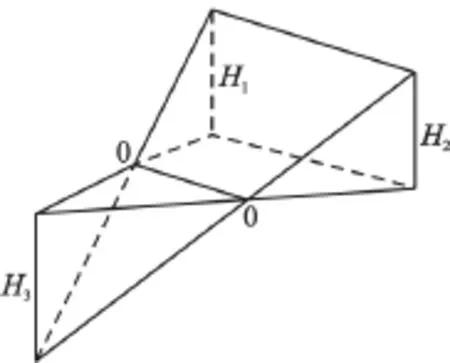
图4 锥体和楔
利用AutoCAD Civil 3D搭建操作视图窗口,支持不同数据来源的原始地形数据和设计面数据,数据计算入口界面和计算结果显示界面分别如图5、图6所示:

图5 土方计算数据入口
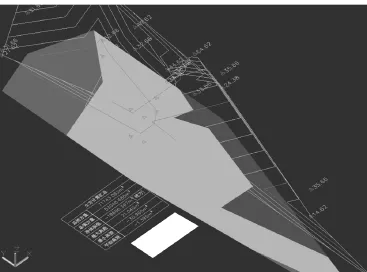
图6 土方计算结果
4 结 论
利用改进后的逐点插入法生成狄洛尼三角网,并结合具有三维显示引擎的AutoCAD Civil 3D,对外业测量数据进行三维展示,通过等高线构成算法和DTM挖填方算法,实现三维环境中的等高线生成和土方量计算,以可旋转、可漫游的方式对数据进行立体展示,从而更真实地表达外业实测地貌形状,更直观地分析挖方、填方的剖面构成,更准确地计算挖填方土方量。
[1] 刘永和,王燕萍,齐永安.一种简单快速的Delaunay三角网逐块生成算法[J].测绘科学,2008(6):133~135.
[2] 许丽敏,薛安.基于Delaunay三角网与Voronoi图联合提取等高线骨架的地形重建算法研究[J].北京大学学报, 2009(4):647~652.
[3] 林伟明,林青海.南方CASS成图软件中三角网对工程量计算的探讨[J].四川水力发电,2012(6):92~94.
[4] 关金华,赵远方,胡金阳等.基于TIN的工程土方量计算[J].矿山测量,2011(6):69~72.
[5] 徐朱,方强,翟辉.基于TIN的土石方计算研究[J].江苏科技信息,2014(13):39~41.
The Analysis of Contour and Earthwork Calculation Based on Delaunay Triangulation
Zhou Hao,Cai Huan
(Tianjin Institute of Surveying and Mapping,Tianjin 300381,China)
For the purposes of displaying External measurement data in three-dimensional model,the author used the improved method of inserting point by point to build the Delaunay triangulation,combined with AutoCAD Civil 3D,so it can draw contours and calculate the cut and fill earthwork square in three dimensional environment,this can better fit the terrain contour movements,can visually analyze the location and earthwork of excavation and filling side,in short,it changes the use of AutoCAD applications from the traditional two-dimensional model to three-dimensional model.
delaunay triangulation;contour;earthwork calculation
1672-8262(2016)01-110-04
P208.1,P209
B
∗2015—12—23
周浩(1988—),男,工程师,研究方向:地理信息系统。
天津市国土资源和房屋管理局科研项目(津国土房科验字[2015]第022号)

