无人机在高原山地环境下航摄轨迹的规划
黄书捷
(漳州市测绘设计研究院,福建漳州 363000)
无人机在高原山地环境下航摄轨迹的规划
黄书捷∗
(漳州市测绘设计研究院,福建漳州 363000)
在高原、山地地形起伏较大的环境下,无人机对点状、线状、面状多个目标拍摄时的轨迹需要进行最优化规划。总体航迹规划分为两个阶段:全局规划阶段,即对多个目标进行全局最短路线规划;局部规划阶段,即为躲避地形威胁,对最短路线中,目标点之间不符合要求的路线进行重规划,最终得到最优的路线轨迹。分别采用蚁群算法和A∗算法进行全局规划和局部规划,仿真结果表明了本文轨迹规划方法的有效性及高效性。
无人机航线;分段规划;蚁群算法;A∗算法
1 引 言
由于传统航空摄影受天气、航空管制等诸多条件的限制,成本高,时效性较差。无人机摄影测量相对传统航测具有灵活,高效,机动性能好等特点,在高山等高分辨率遥感影像数据缺乏的地区,具有很大的应用前景。近年来,无人机摄影测量技术发展迅速,已广泛应用于农业、林业、水利、交通、国土资源等国民经济各领域。在高原地区,需要定期对道路,桥梁,铁路,电力线路等进行巡检,由于环境恶劣,需要投入大量人力物力,成本高,效率低,因此,使用无人机进行巡检,具有很大优势。
无人机航迹规划是指在一定的约束条件下,比如无人机的机动性能、地形环境限制、燃油量等因素,从起始点出发,经过预定的任务点,到达目标点的最优飞行轨迹。本文首先对地形进行仿真,建立三维模型,使得规划环境更加贴近实际,然后将航线规划分为全局规划和局部规划,全局规划是TSP(Traveling Salesman Problem)问题,不考虑无人机机动能力和地形威胁;局部规划是针对全局路线中两任务点之间,根据无人机的性能,飞经的地理环境、威胁环境等因素,对已知目标规划出满足要求的航迹。蚁群算法(ant colony optimization,ACO)是一种新的启发式仿生类并行智能进化算法,近几年在优化领域中出现不久,最早成功应用于解决TSP问题[1],在解决TSP问题上具有较高效率,本文采用蚁群算法得到全局最短路径。局部规划是两任务点之间的线路规划,目前常用解决方法有:动态规划法、快速随机搜索树算法、遗传算法、概率地图法、Voronoi图法和启发式搜索算法等。启发式搜索算法最早运用在计算机和机器寻路等领域,在较大的搜索空间下搜索时间很短,效率高。目前,研究最多的是启发式A∗算法[2]。本文将采用启发式A∗算法进行局部航线规划。
2 主要威胁源及限制条件
对于测绘型无人机,主要的威胁源为地形威胁及大气条件威胁,主要考虑的限制条件有无人机的转弯角度限制,飞行高度限制以及航迹的长度约束以及燃油限制等。
2.1地形限制
对于地形的限制,实验中采用随机函数法进行仿真,通过数学模型函数,来模拟已知地形的原始三维地形。数学模型函数形式为[3]:
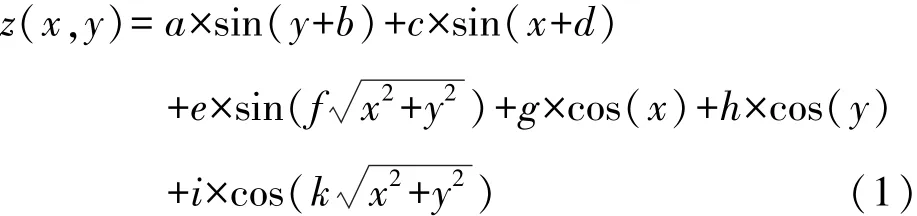
其中,x,y是水平面上的点坐标,z是水平面上对应的坐标点的高度。a,b,c,d,e,f,g是常系数。通过控制这几个常系数的取值,可以对各种实际地貌的地形进行模拟,作为在地面已探知的任务区域的地形地貌等信息。
接着采用式(2)生成山峰威胁模型,函数形式为[3]:

其中,zi为第i个山峰最高点的高度,xoi,yoi对应第i个山峰最高点在水平面上的坐标,xsi,ysi的值决定了第i个山峰的坡度,通过改变这两个值,可以控制x轴方向和y轴方向的陡峭程度。
将地形模型和山峰模型进行叠加,即选取两个模型中较高的点,函数形式为[3]:
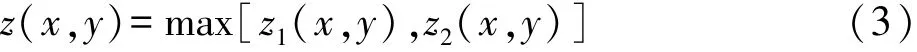
通过叠加融合,模拟了真实的地形地物,再现了山峰威胁模型,用此模型作为航线规划环境,简化了航线规划的复杂程度。
2.2大气威胁
在起飞阶段,为了获得足够的爬升力,无人机需要逆风起飞,而各种不同的无人机对于风速的具体数值有着严格的限制。无人机在升空后,在巡航阶段可能会遇到天气变化,云层将会给无人机带来威胁,无人机表面可能会结冰或者无人机电子设备受到云层中雷电的袭击而破坏[4]。由于天气的变化情况十分复杂,本文不对此威胁进行模拟。
2.3无人机约束条件
无人机由于制造水平,成本的限制以及用途的不同,不同类型的无人机性能各异。在航迹规划中,需要考虑的限制如下:
(1)角度限制。由于飞行器机动性能的限制,需要考虑飞行器的最大爬升/下降角和最大拐弯角。测绘型无人机航拍需要所得的相片比例尺一致,所以无人机不进行垂直方向的机动,可不考虑爬升角和下降角。
(2)高度限制。无人机必须与地面保持足够的安全距离,才能有效地降低触地概率。
(3)最大航迹长度限制。由于无人机受燃油有限负荷或者到达时间的限制,因此需要对航迹限定最大允许长度Lmax。当无人机飞行状态不同时,如爬升、下滑及平飞时的油耗系数是不一样的。规划过程中,长度大于最大允许长度的航迹需被排除。
3 航迹规划
3.1地图数据表示方法
由地图学的基本理论,我们将航拍目标分为点状目标、线状目标和面状目标。点状目标是指按照设定的分辨率要求,单张照片可以覆盖的地物,如独立房屋等。在线状目标具有一定长度且比较狭窄的地物,如河流,公路,堤坝等。对于此类地物,无人机必须沿其中心线飞行进行拍摄。面状目标是指占有比较大地理空间区域的地物,如湖泊,森林,城镇等。对于面状目标的轨迹规划可见参考文献[5]。
3.2全局航迹规划
3.2.1TSP问题
旅行商问题,即TSP问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须确定每个城市的拜访顺序,得到最终的拜访路径。每个城市只能拜访一次,而且最后要回到原来出发的城市,问题的关键在于要求拜访的最终路径最短。无人机的航线规划问题是从起始点出发,经过若干任务点,再回到回收场,类似于TSP问题。
3.2.2蚁群算法原理
研究表明,蚂蚁在行进过程中会留下一种分泌物,而这种分泌物可以引导后面的蚂蚁对路径的选择。一条路径上走过的蚂蚁越多,留下的分泌物就会越多,而分泌物越多,蚂蚁选择这条路径的概率就越大。因此,蚂蚁群体的集体行为实际上形成一种学习信息的正反馈现象,通过这种信息交流,促使蚂蚁找到通向食物的最短路径[6]。整个蚁群就是通过这种信息素进行相互协作,形成正反馈,从而使多个路径上的蚂蚁都逐渐聚集到最短的那条路径上。
3.2.3蚁群算法基本流程
以TSP问题为例,蚂蚁系统具体包括了以下三个方面的内容。
第一、初始化。首先构造一个禁忌表,用来记录每一只蚂蚁走过的节点,将蚂蚁所在的起始节点放入禁忌表;接着还要对每条路径上的信息素的浓度进行初始化,假设初始浓度为r。
第二、选择路径。计算蚂蚁到其他节点的概率分布。概率的计算如式(4):

式(4)表示蚂蚁在t时刻由节点i选择节点j的概率。τij(t)为i,j路径上的信息素浓度,ηij是j相对于i的可见度(在TSP问题中常以距离的倒数表示),α,β分别表征信息素和可见度在概率计算中的权重,其值越大,则信息素和可见度对于蚂蚁选择下一个节点的影响越大。allowed是指不在蚂蚁禁忌表中的节点集合,即蚂蚁还未经过的节点。由于禁忌表的制约,蚂蚁不会选择已经在禁忌表中的节点。
第三、信息素更新。由于各条路线上的信息素也会随时间逐渐蒸发,而蚂蚁经过会增加信息素浓度,所以需对信息素进行更新。ρ为信息素的残留因子,1-ρ表示信息素的挥发因子。经过tn个时间单位后,根据式(5)式(6),对各条路线上的信息素进行更新。

△τij表示第k只蚂蚁在本次循环中,节点i,j之间的路径上留下的信息素增量,用式(7)计算。

其中,Q为常数,Fk表示第k只蚂蚁在本次循环中的目标函数值(一般为路径的总长度)[7]。
蚁群算法一般流程基本步骤描述如下:
(1)初始化蚂蚁数量m,最大循环次数NC_max,初始信息素值和禁忌表;
(2)开始迭代,将各蚂蚁的初始出发点放入禁忌表中;
(3)计算每只蚂蚁移至下个节点的概率;
(4)按概率(采用轮盘法)选择并移动至下个节点,将此节点加入禁忌表;
(5)如果蚂蚁走遍所有节点则执行(6),否则返回(3);
(6)计算蚂蚁该次总路线长度,并记录当前最短路线;
(7)用式(5),式(6),式(7)更新全局信息素;
(8)若迭代次数达到NC_max则输出最优解,退出算法,否则返回(2)继续执行[8]。
3.3局部航迹规划
3.3.1A∗算法原理
A∗算法是在1968年由Hart,Nilsson,Raphael等人提出的一种启发式的搜索算法,用于搜寻最短路径,其被广泛运用于寻找目标和图形遍历[9]。无人机航迹规划本质上是从起点不断扩展航迹节点,最终找到终点。A∗算法进行航迹搜索时,通常将规划环境按一定比例划分为二维或者三维网格的形式,每个节点可以往任意方向扩展,按代价函数找到最小代价点。由于需要考虑无人机的机动性能,所以要根据无人机的最大转弯角来限定可以扩展的节点。有时出现障碍阻碍了最小代价点的扩展,此时要退回上一个节点,寻找次优代价点继续扩展,最终找到最小代价轨迹。其中A∗算法的航迹代价函数为:

其中x为当前节点,g(x)为从起始点到该点的真实代价,u(x)为启发函数,表示当前节点到目标位置代价的估值,f(x)即为搜索空间节点的总代价[10]。
3.3.2算法流程
搜索过程中需要用到以下几个关键的矩阵:①搜索图G,存储当前已生成的路线;②OPEN列表,存储已经生成但还没进行扩展的结点;③CLOSED表,存储已经扩展过的结点。同时,每个结点的代价估计值f和g也包含在两张列表中。
A∗算法的流程步骤如下:
(1)生成一个搜索图G,此时图中只包含了起始点s,同时把起始点s加入到OPEN列表中。
(2)生成一个CLOSED列表,初始值为空。
(3)循环:
①如果OPEN列表为空,则退出循环,搜索失败。
②如果目标点被加入CLOSED列表,说明目标点找到,则退出循环,搜索成功。
③对当前节点n可选择的每一个节点ni进行判断,如果ni已经在CLOSED列表或者OPEN列表中,则将其跳过,否则将其加入OPEN列表中,把当前节点n作为节点ni的父节点。
④在OPEN列表中寻找f值最小的节点m,然后把当前节点n放入CLOSED中,把当前节点换成节点m,把当前节点移动的方向记录在搜索图G中,把f和g的值分别记录在OPEN和CLOSED列表中。
(4)如果找到目标点g,顺着搜索图G,得到从目标点g到起始点s的路径,获得最优路径,成功退出[11]。
4 仿真实验
4.1 航迹规划环境模型
利用式(1),式(2),得到原始地形和山峰模型,通过对原始地形和山峰模型进行融合叠加,得到航迹规划的环境模型得到规划环境模型,规划空间为100× 100×300的区间,如图1所示。式(1)中参数取值为:a =20,b=0,c=20,d=3,e=8,f=1,g=0,h=20,i=0。山峰数为7,参数取值如表1所示。4.2 规划区域

山峰威胁模型参数设置 表1

图1 环境模型
如图2所示。1,2,3,6,9为点状目标,4与5的连线为线状目标,7,8为面状目标航拍路线的切入点以及退出点。

图2 航线规划区域
文中分别采用蚁群算法和A∗算法,matlab2013a中进行全局和局部规划仿真实验。
4.3仿真实验
4.3.1全局规划仿真实验
为保持比例尺一致,无人机飞行高度不变,不进行垂直方向机动,只进行水平机动,飞行高度为100,表2为航线规划时蚁群算法的参数设置。以点1为无人机的起飞点与降落点,图3为用蚁群算法得到的最短路线,全局规划阶段用时6.6 s。但是从三维图4中可以看出点1与点9之间的航线直接穿越了山体,显然不符合航线规划的要求,需要对点1~点9之间的航线进行重规划。

蚁群算法参数设置 表2
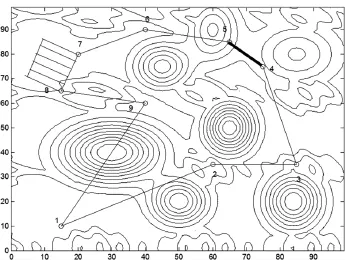
图3 蚁群算法所得最短航线

图4 蚁群算法所得最短航线三维图
4.3.2局部航线重规划
为证实A∗算法在局部规划中的有效性,本文先取区域中的(0,0)为起始点,(100,100)为目标点,进行仿真实验,得到航线如图5,可以看出航线有效地避开了地形的威胁,满足规划要求。
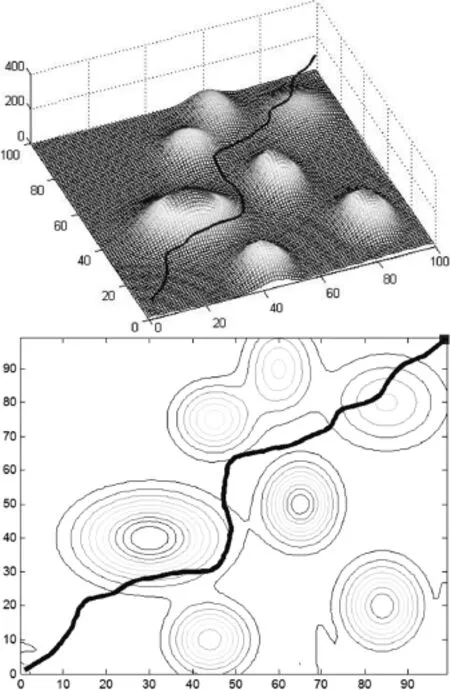
图5 A∗算法所得最优航线
接着对点1和点9之间的航线重规划,得到航线如图6所示。局部重规划用时1.8 s。

图6 点1与点9之间最优航线
4.3.3全局规划航线与局部规划航线合成
将全局规划的最短航线与局部规划的最优航线进行合成,得到了最终的无人机规划航线,两阶段的航线设计用时为8.4 s,如图7所示。

图7 合成的最终航线
4.3.4结果分析
航迹规划所得的结果表明:
(1)基于航迹约束条件,通过分阶段设计,能够规划出一条满足要求的航迹,总设计时间为8.4 s,算法高效,具有工程实用性。
(2)对图7分析可知,所得的最优航迹有效的避开了威胁,实现了无人机的安全飞行。
5 结 语
本文将航线设计分为两个部分,首先用蚁群算法规划出最短航线,接着采用A∗算法对最短航线中不符合航线要求的航线段进行重规划,最后进行航线合成得到最终航线。文中详细阐述了蚁群算法,A∗算法的原理及算法流程,很好地满足航线设计的要求,而且分阶段规划后,仅需要对部分航线段重规划,减少了处理时间,效率高,能够满足高原、山地等地形起伏较大的地区航测无人机航线规划。同时,该方法也可以用于低空无人机在城市中飞行的航线规划。
[1] Mettler B,Bachelder E.Combining on-and offline optimization techniques for efficient autonomous vehicle’s trajectory planning[C]//AIAA Guidance,Navigation,and Control Conference,San Francisco,CA.2005.
[2] 郑家良.无人机航迹规划与导航的方法研究及实现[D].成都:电子科技大学,2009.
[3] Nikolos I K,Valavanis K P,Tsourveloudis N C,et al.Evolutionary algorithm based offline/online path planner for UAV navigation[J].Systems,Man,and Cybernetics,Part B:Cybernetics,IEEE Transactions on,2003,33(6):898~912.
[4] 戴定川,盛怀洁,边晓利.无人机航迹规划分段需求分析[J].战术导弹技术,2011(6):63~69.
[5] 陈海,王新民,焦裕松等.一种凸多边形区域的无人机覆盖航迹规划算法[J].航空学报,2010,31(9):1802~1807.
[6] Macro Dorigo,Mauro Birattari,Thomas Stiitzle.Ant Colony Optimization[J].IEEE Computational Intelligence Magazine,2006(8):30~35.
[7] Sharon Rosenberg and Kathleen A Meade.A practical guide to Adopting the universal verification Methodology(UVM) [M].Cadence Design Systems,2010.
[8] 马良,朱刚,宁爱兵.蚁群优化算法[M].北京:科学出版社,2008.2
[9] 丁明跃,郑昌文,周成平等.无人飞行器航迹规划[M].北京:电子工业出版社,2009.1
[10] Hart,Nilsson,Raphael,A Formal Basis for the Heuristic Determination of Minimum Cost Paths.IEEE Transactions on Systems Science and Cybernetics SSC4 4(2):100-107.
[11] Nils J.Nilsson.人工智能[M].北京:机械工业出版社, 2000.9
Trajectory Planning of UAV in Plateaus,Mountainous Environment
Huang Shujie
(Zhangzhou Geomatic Institution,Zhangzhou 363000,China)
The trajectory of UAV must be planned when UAV is about to shooting the punctate,linear,planar multiple targets in the undulating environment such as plateau and mountainous terrain.Overall trajectory planning is divided into two phases:global planning stages,namely to plan global shortest route for multiple targets;local planning stages,re -planning the route between the destination points which do not meet the requirements in order to avoid the terrain threat,and ultimately get the best route trajectory.Ant colony algorithm and A∗algorithm were used in global planning and local planning.The results of the simulation show the effectiveness and efficiency of the trajectory planning method.
UAV trajectory;segmented planning;ant colony algorithm;A∗algorithm
1672-8262(2016)01-53-06
P237
A
∗2015—10—20
黄书捷(1990—),男,硕士,助理工程师,主要从事GPS/INS组合导航研究。

