起伏地形下各向异性的2D大地电磁无网格法数值模拟

嵇艳鞠, 黄廷哲, 黄婉玉, 李桐林, 王远*

1 吉林大学仪器科学与电气工程学院， 长春 130026 2 吉林大学地球探测科学与技术学院， 长春 130026 3 地球信息探测仪器教育部重点实验室， 长春 130026



起伏地形下各向异性的2D大地电磁无网格法数值模拟

嵇艳鞠1,3, 黄廷哲1, 黄婉玉1, 李桐林2, 王远1*

1 吉林大学仪器科学与电气工程学院， 长春 130026 2 吉林大学地球探测科学与技术学院， 长春 130026 3 地球信息探测仪器教育部重点实验室， 长春 130026

作为一种基于节点的计算方法，无网格法具有构造高阶导数方便，自适应分析便利的优点，特别适合复杂地质构造的数值模拟.本文针对实际地球物理勘探中存在的起伏地形和各向异性的地电结构，提出用无网格法来模拟大地电磁响应，采用复合二次径向基函数构造了形函数，推导了大地电磁无网格法等价线性方程组，研究了系数矩阵的压缩存储方法以及大型稀疏复线性方程组快速求解算法，实现了起伏地形下各向异性的2D大地电磁高精度数值模拟.基于层状模型验证了算法的正确性，计算结果表明：无论是TM模式还是TE模式，计算相对误差均小于1%；通过对地垒和地堑模型的模拟，得出了起伏地形对视电阻率和相位的影响规律；对起伏地形下含有不同各向异性系数异常体的模型进行了数值模拟，为开展复杂地质结构的电磁场特征研究以及地形校正奠定了理论基础.随着计算科学的快速发展，无网格法必将成为新的高精度电磁场数值模拟方法.

无网格法； 径向基点插值； 起伏地形； 各向异性； 大地电磁

1 引言

我国多山区丘陵，山区面积约占国土面积的2/3，地形是影响电磁场分布的主要因素之一(张继锋等，2013).随着现代观测技术的不断进步以及认识水平的不断提高，电性参数的各向异性问题逐渐引起了人们的广泛重视，成为电磁勘探领域研究的热点.只有深入地研究电磁波在起伏地形和各向异性介质中的传播特征，才能得到更接近实际地质情况的解释，从而更加准确地认识地球内部的电性结构和属性.

大地电磁测深法(Magnetotelluric Sounding，简称MT)是通过观测和研究天然交变电磁场从而确定地球内部电性结构的一种电磁勘探方法，被广泛应用于地壳、上地幔的研究中(李金铭，2005).近些年来，学者们提出了多种大地电磁数值模拟方法(Mackie et al.，1993；徐世浙，1994；Pek and Verner，1997；Li and Pek，2008；Qin et al.，2013)，主要集中在基于网格剖分的有限元、有限差分等方法.在各向异性和起伏地形研究方面，Pek等(2002)推导了1-D各向异性模型的大地电磁拟解析解.Key和Weiss(2006)提出了二维大地电磁自适应有限元算法，较好地模拟了起伏地形和倾斜界面的电磁响应.霍光谱等(2015)采用有限差分方法模拟了带地形的各向异性模型并进行了实例分析.尽管基于网格的方法在大地电磁数值模拟中取得了很好的效果，但由于剖分网格的制约存在着计算缺陷，如网格畸变造成的数值精度较低等(Liu and Gu，2005；程玉民，2015).

为了解决这些难题，采用不基于节点拓扑连接关系(网格)产生逼近函数的无网格方法应运而生.作为一种新兴的数值计算方法，无网格法(Meshfree Method,MM)是有限元等传统方法的补充和发展，在近十几年里得到了广泛的关注.在地球物理电磁勘探领域，冯德山等(2013)利用无单元Galerkin法进行了探地雷达的正演模拟，Wittke和Tezkan(2014)采用径向点插值的无网格局部Petroy-Galerkin方法，在不考虑地形影响的条件下，对二维异常体的大地电磁响应进行了模拟.李俊杰和严家斌(2015)研究了二维大地电磁中无网格与有限元的耦合算法并探讨了影响无网格法精度的主要因素，但在研究中仅涉及分块均匀模型，未考虑各项异性和地形因素.

本文在前人的研究基础上，提出用无网格法来模拟实际探测中的起伏地形和各向异性问题，基于复合二次径向基函数(Multi-Quadric Radial Basis Function，MQ-RBF)构造了无网格法的形函数，假设各向异性介质的电性主轴一个垂直于层面方向，另外一个平行于层面方向，构造了各向异性介质的电导率张量模型，通过Krylov子空间的预处理和正则化拟残量极小(Quasi-Minimal Residual，QMR)方法实现了大型稀疏复线性方程组的精确快速的求解，实现了起伏地形下各向异性的2D大地电磁数值模拟.

2 无网格大地电磁数值模拟算法

采用无网格法进行大地电磁数值模拟的主要思路是首先将整个区域离散为各个节点，在局部支持域内构造各节点的无网格形函数；从频率域麦克斯韦方程出发，分别导出二维模型平行走向电场和磁场分量所满足的偏微分方程和边界条件，将边值问题转化为泛函，求取泛函极值得到等价的无网格线性方程组；求解线性方程组得到电场和磁场的数值解，通过求解辅助场得到视电阻率和阻抗的相位.

2.1 基于复合二次径向基函数的形函数构造

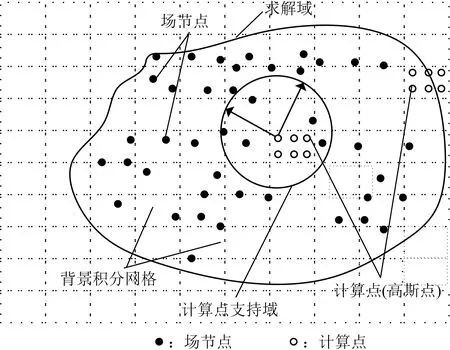
图1 无网格法区域离散示意图Fig.1 The sketch map of regional discretization based on meshfree method

无网格法的求解区域离散示意图如图1所示.由于无网格法是一种不依赖于网格来构造形函数的方法，因此在无网格法中引入了支持域的概念.支持域的形状可根据计算需要和场值的变化进行设定.一般设定高斯点为计算点，若节点位于计算点的支持域内，则该场节点参与构造该计算点的形函数.

在求解域Ω内，任一节点XT=(x,y)的场变量u(X)的在局部支持域内的径向基点插值(Radial Point Interpolation Method,RPIM)表达式为

=RT(X)a+PT(X)b,

(1)

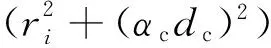
式(1)中有(n+m)个变量，需添加m个约束条件：

(2)

联立式(1)和式(2)可得到如下矩阵方程：

(3)

求解式(3)可得到

(4)

可将式(1)重写为

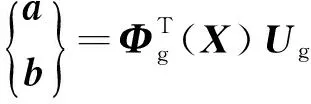
(5)

式中的RPIM形函数可表示为

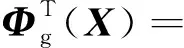
2.2 等价线性方程组的推导

设平行层面电导率为σ∥，垂直层面电导率为σ⊥，走向为z轴，y轴垂直向上，二维各向异性MT边值问题归纳如下(徐世浙，1994)：

(7)

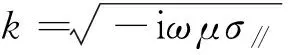
(8)

其中α为各向异性介质的电性主轴与地面坐标系的夹角.

定义各向异性系数r为平行电导率和垂直电导率的比值平方根，通过r的大小来表征介质的各向异性程度：

(9)

各向异性大地电磁边值问题(7)的等价泛函为

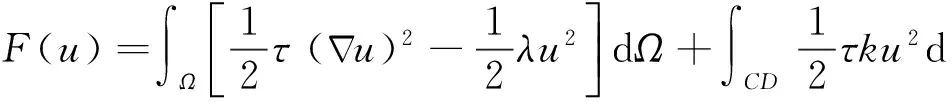
(10)

求取泛函F(u)对场量u的偏导数，将u(X)=ΦT(X)U带入，令泛函F(u)对场量u的偏导数为0，从而得到矩阵表达式

K u=b,

(11)

其中：

-∫ΩλΦiΦjdΩ+∫CDτkΦiΦjdΩ,

上边界AB为本质边界，设其场值为1个单位，为了加载本质边界，将系数矩阵K和右端项b分别修正为如下形式：

(12)

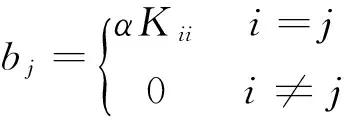
(13)

这样使系数矩阵只在两处发生了变化，本质边界条件处理较为简单.为了方便数值积分，将求解域Ω划分为若干积分单元，在求解域和边界处的积分均采用高斯积分实现.需要指出的是，这里的积分单元(背景网格)是与节点及其支持域无关的，只要方便积分即可.

2.3 大型稀疏复线性方程组的求解

由于支持域的存在，无网格法形成的系数矩阵K是大型的、稀疏的复线性方程组，为了节省内存，采用MATLAB自带的稀疏存储函数对系数矩阵进行压缩存储.Krylov子空间方法被认为是一种求解大型稀疏线性方程组的有效方法(柳建新等，2009)，基于Krylov子空间的迭代方法收敛速度快，求解精度高，而且稳定性好.本文采用基于Krylov子空间的正则化拟残量极小(QMR)方法进行线性方程组求解，对方程组(11)求解即可得到各个节点处的场值.

在程序设计实现中，首先读取模型的输入参数，包括频率参数，节点坐标，背景网格信息，支持域，形状参数，极化模式等；若为TE极化模式，则计算区域包含空气层，若为TM极化模式，则不含空气层.对所有背景网格进行外循环，对所有高斯积分点内循环，搜索背景网格中支持域内的有效节点并计算支持域内系数矩阵，当所有高斯积分点(计算点)和背景网格循环完毕之后，加载本质边界条件得到线性方程组，求解线性方程组得到主场值，最终求得相应的视电阻率和阻抗相位.

3 模型计算及分析

3.1 算法验证

为验证无网格数值算法的正确性，建立求解区域为20km×20km的层状模型，场节点均匀分布，节点间距均为100m.第一层电阻率为1000Ωm，厚度为2km，第二层电阻率为100Ωm，厚度为4km，底层电阻率为10Ωm.表1和表2给出了层状模型下视电阻率和相位的解析解和无网格法的计算结果.由于频率越高趋肤深度越浅，导致视电阻率和相位的计算相对误差随着频率增大而增大，但是无网格法的数值模拟精度仍然很高，相对误差变化范围在1.4×10-7～9×10-3之间，最大相对误差不超过1%，验证了无网格法是一种高精度的数值计算方法，可以有效地计算复杂条件下的大地电磁响应.

为了验证本文求解各向异性问题的正确性，建立如图2所示的层状模型，第一层和第三层为各向同性介质，电阻率为100Ωm，第二层为各向异性介质，平行层面电阻率为10Ωm，垂直层面电阻率为1000Ωm，介质的电性主轴与地面坐标系的夹角为30°.第一层和第二层层厚分别为1km和2km.计算区域大小为20km×20km.

图3为在计算区域内地面中心点处的无网格法数值解与Josef推导的拟解析解的对比图，从图中可以看出，在各个频率下无网格法数值解与拟解析解两者高度吻合.统计结果表明，无网格法解与拟解析解的均方根相对误差不超过1%，充分验证了无网格法求解各向异性大地电磁问题的正确性.

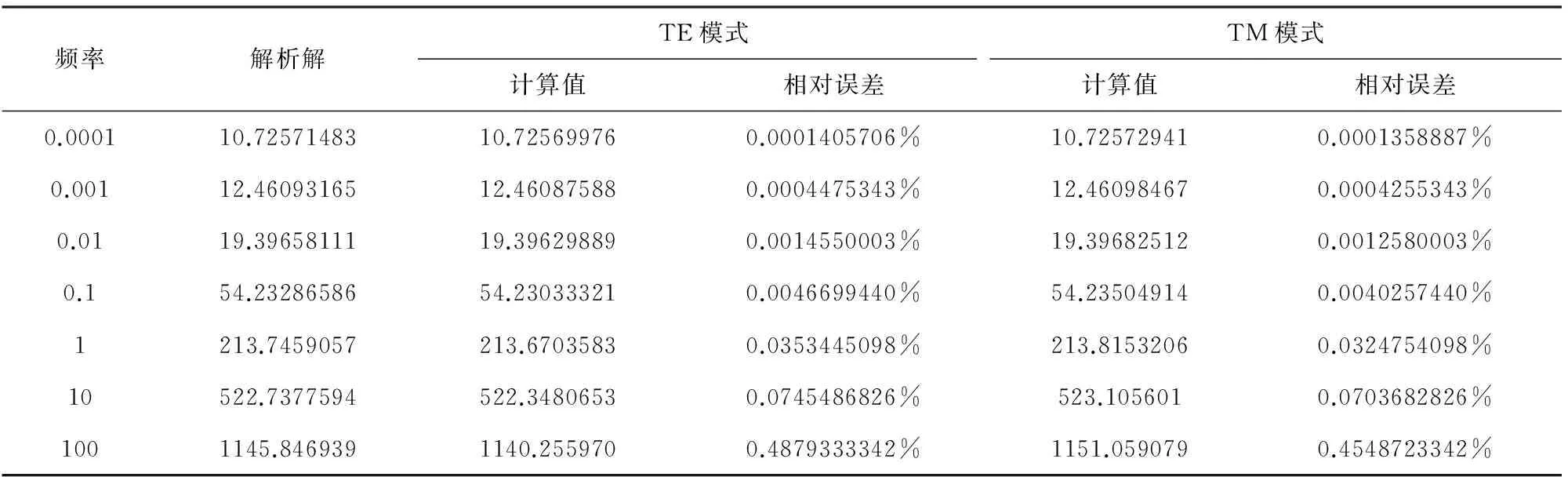
表1 层状模型视电阻率数值解的相对误差

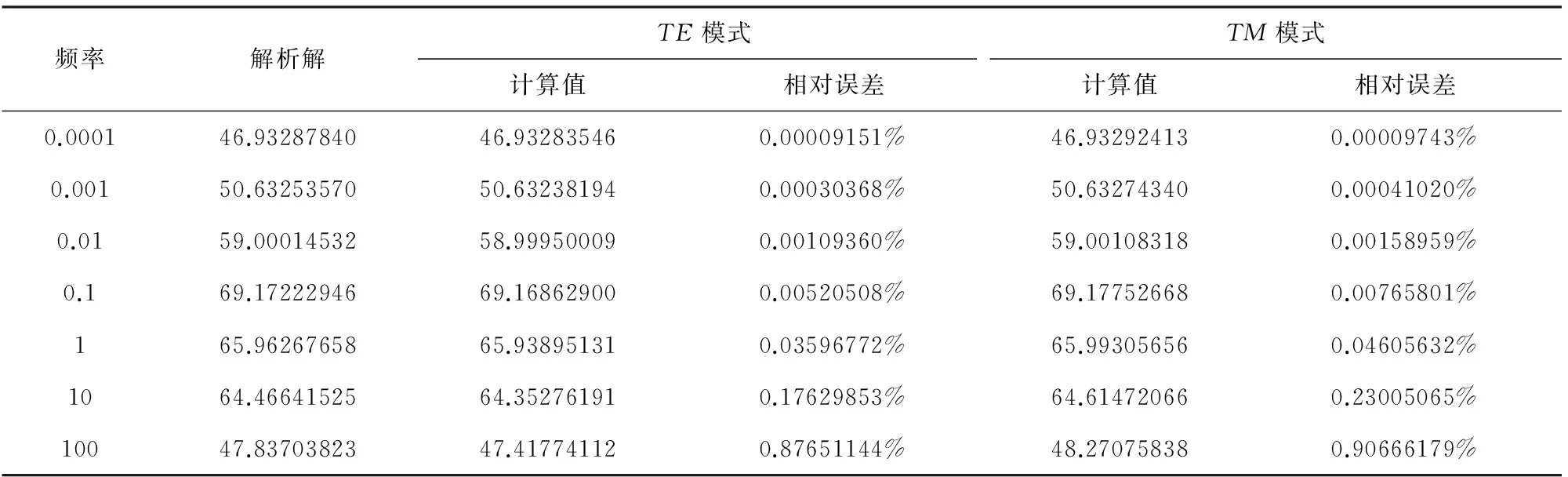
表2 层状模型相位数值解的相对误差

图2 各向异性层状模型示意图Fig.2 Anisotropic layered model schematic diagram

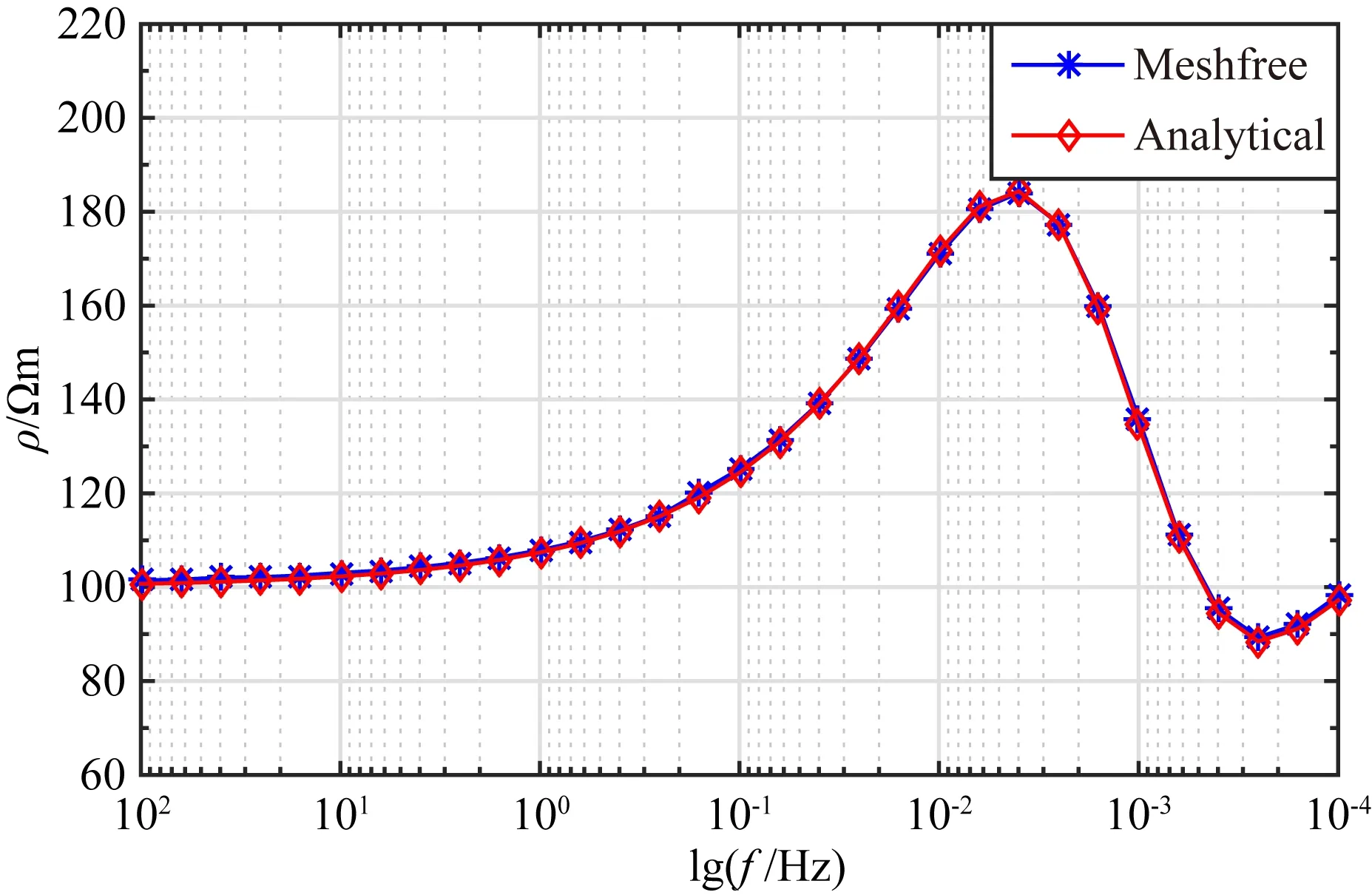
图3 各向异性层状模型拟解析解与无网格法解对比图Fig.3 Comparison between meshfree solution and analytical solution of anisotropic layered model

3.2 起伏地形数值模拟

为了模拟实际起伏地形的大地电磁响应，分别建立地垒和地堑模型如图4和图5所示.起伏地形的宽度均为2km，地堑和地垒的倾角均为45°.为了探究不同起伏高度下对大地电磁响应的影响规律，分别设置了500m和200m两种高程.横轴代表水平距离，均匀空间的电阻率均为100Ωm.

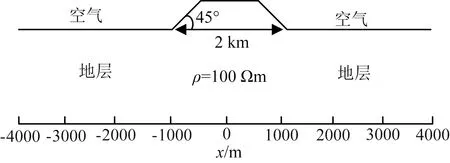
图4 均匀半空间下的地垒地形Fig.4 Horst terrain in homogeneous half space

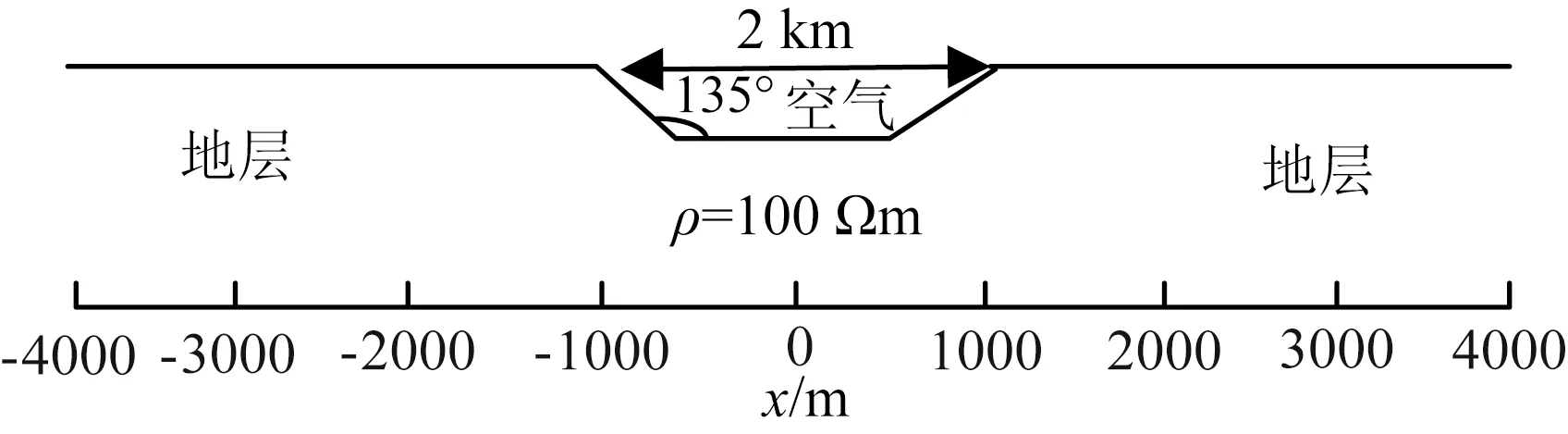
图5 均匀半空间下的地堑地形Fig.5 Graben terrain in homogeneous half space

图6和图7为地垒地形下视电阻率和相位的计算结果.从图中可以看出，在地垒地形的拐点位置，视电阻率和相位都发生了剧烈的变化，地垒地形的存在导致TM模式视电阻率减小，500m高程使起伏处的视电阻率相对变化率高达80%，出现了大低阻异常中夹小高阻异常的复杂现象；而TE模式视电阻率增大，500m高程使起伏处的视电阻率相对变化率达到8%；随着高程的降低，视电阻率的相对变化率分别降到了40%和2%；在大地电磁测量频率范围内，复杂地形导致TM模式视电阻率出现了假异常，随着频率的增大大异常受影响较小，小异常受到影响较大.

图8和图9为地堑地形下的视电阻率和阻抗相位的计算结果.从图中可以看出，地堑地形导致TM模式的视电阻率增大，500m高程使起伏处的视电阻率相对变化率高达90%，出现了大高阻异常中夹小低阻异常的复杂现象；而TE模式的视电阻率值减小，500m高程使起伏处的视电阻率相对变化率达到4%；随着高程的降低，视电阻率的相对变化率分别降到了40%和1%；在大地电磁测量频率范围内，复杂地形导致TM模式视电阻率出现了假异常，随着频率的增大大异常受影响较小，小异常受到影响较大.

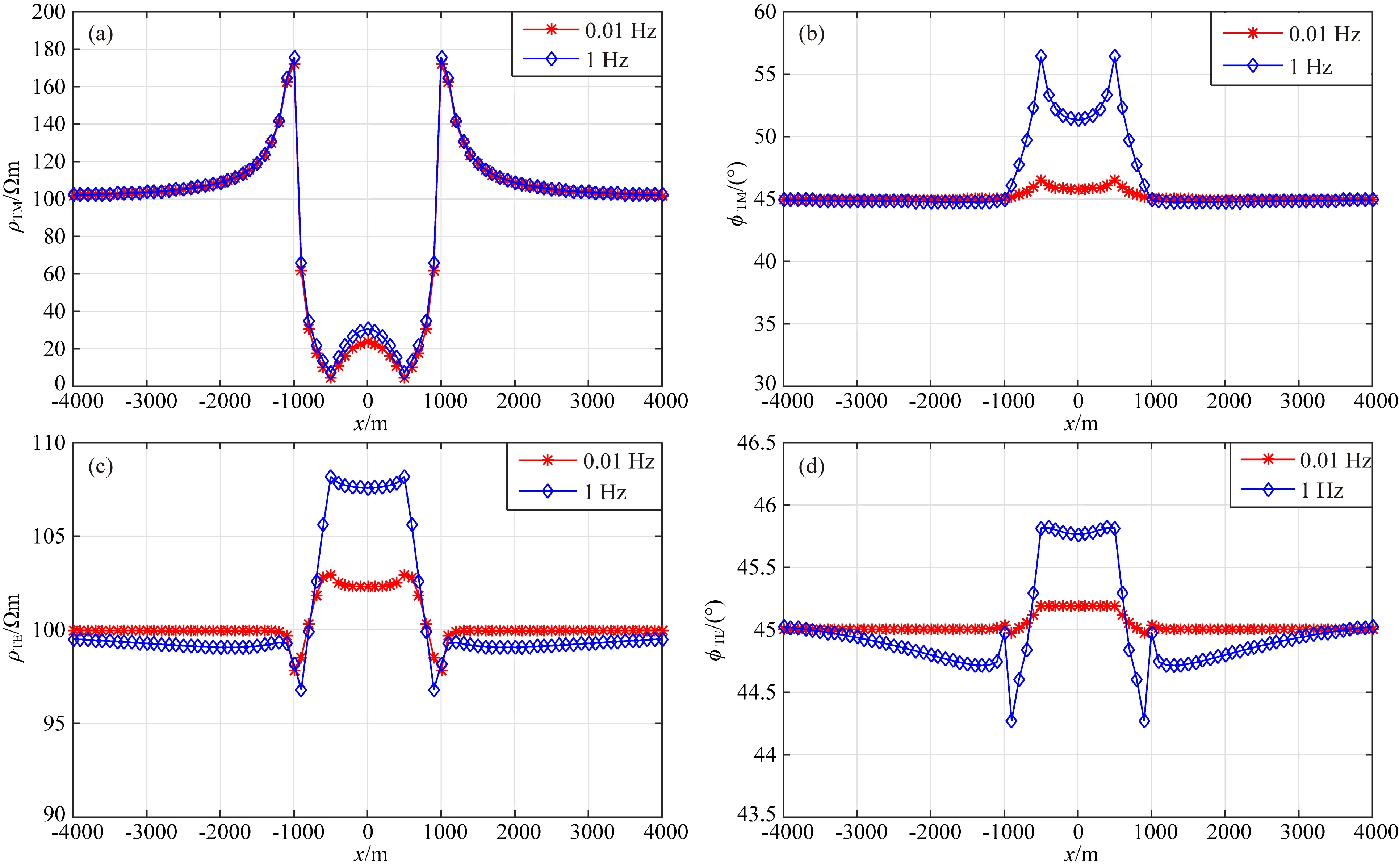
图6 地垒地形下高程500m视电阻率和相位模拟结果(a) TM视电阻率; (b) TM相位; (c) TE视电阻率; (d) TE相位.Fig.6 Simulation results in height 500 m horst terrain(a) TM mode apparent resistivity; (b) TM mode phase; (c) TE mode apparent resistivity; (d) TE mode phase.

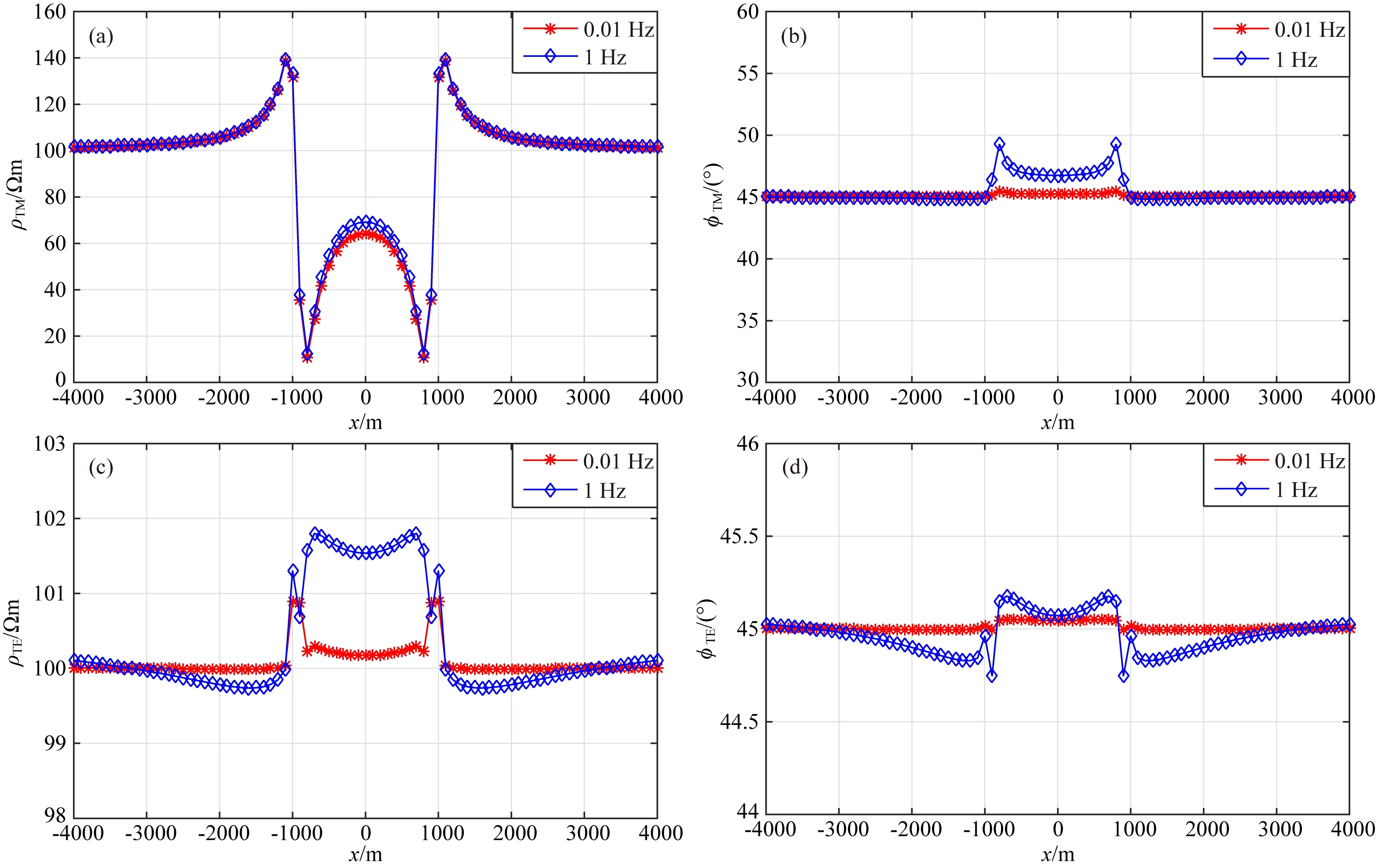
图7 地垒地形下高程200 m视电阻率和相位模拟结果(a) TM视电阻率; (b) TM相位; (c) TE视电阻率; (d) TE相位.Fig.7 Simulation results in height 200 m horst terrain(a) TM mode apparent resistivity; (b) TM mode phase; (c) TE mode apparent resistivity; (d) TE mode phase.

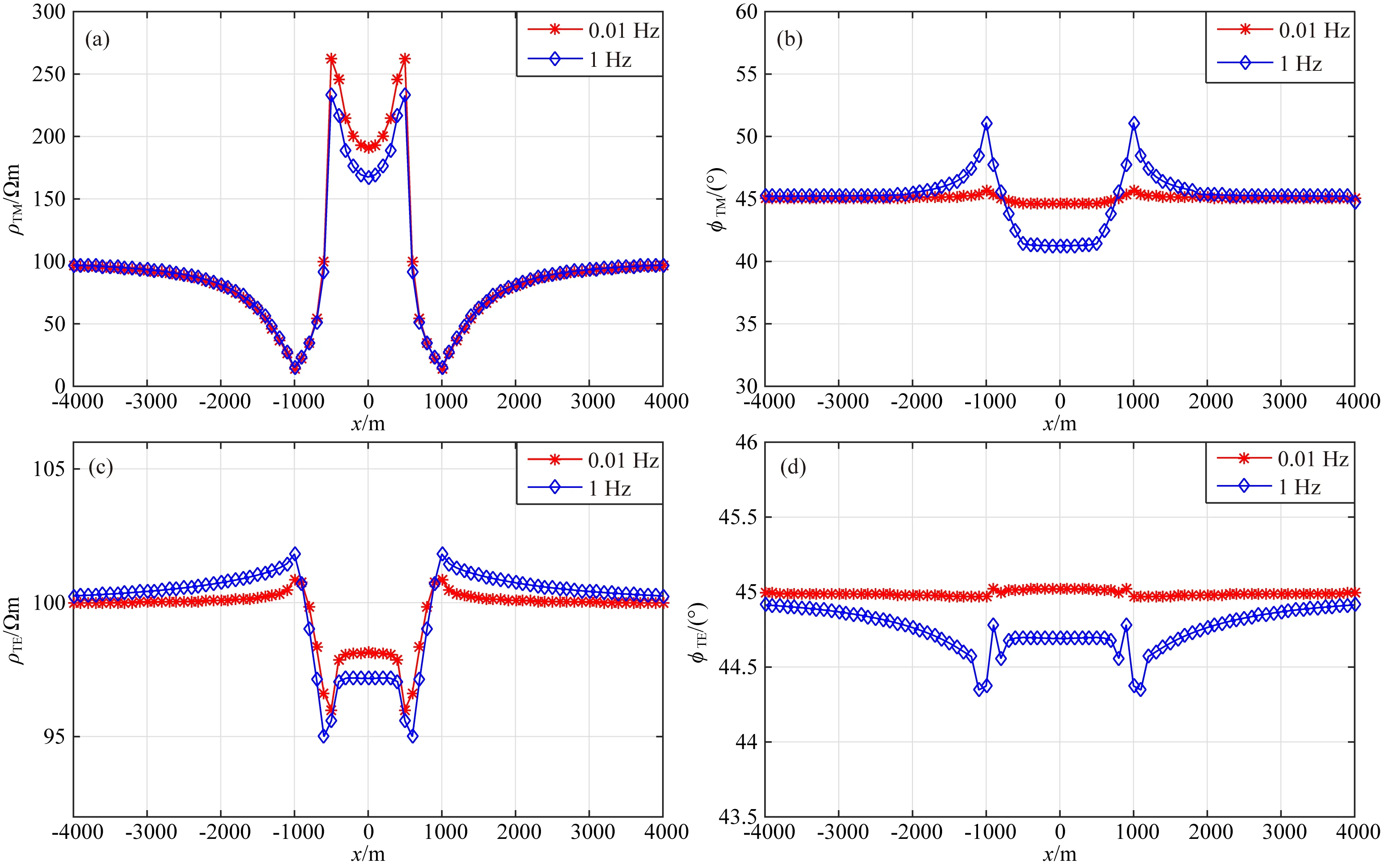
图8 地堑地形下高程500 m视电阻率和相位模拟结果(a) TM视电阻率; (b) TM相位; (c) TE视电阻率; (d) TE相位.Fig.8 Simulation results in height 500 m graben terrain(a) TM mode apparent resistivity; (b) TM mode phase; (c) TE mode apparent resistivity; (d) TE mode phase.

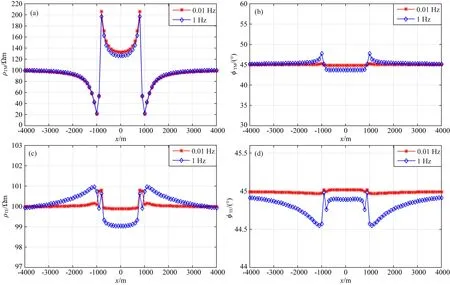
图9 地堑地形下高程200m视电阻率和相位模拟结果(a) TM视电阻率; (b) TM相位; (c) TE视电阻率; (d)TE相位.Fig.9 Simulation results in height 200 m graben terrain(a) TM mode apparent resistivity; (b) TM mode phase; (c) TE mode apparent resistivity; (d) TE mode phase.

综上以上分析，我们可以得出：

(1) 地形的存在使视电阻率和相位都发生了较大的变化，对视电阻率的影响要大于相位，对TM模式的影响要大于TE模式.

(2) 地垒地形TM模式下的视电阻率呈现大低阻异常中夹小高阻异常的复杂现象，而地堑地形TM模式下视电阻率呈现大高阻异常中夹小低阻异常的复杂现象，相对而言地形对TE模式影响较小.

(3) 随着高程的降低，地形对视电阻率和相位的影响逐渐降低.

(4) 在大地电磁测量频率范围内，复杂地形导致TM模式视电阻率出现了假异常，随着频率的增大大异常受影响较小，小异常受到影响较大.

(5) 由于起伏地形对大地电磁视电阻率和相位均产生了重大的影响，因此在数据解释时，需要对地形进行校正，消除地形导致的复杂假异常.

3.3 各向异性体数值模拟

为了进一步分析起伏地形下含有异常体的大地电磁响应特征，分别在地垒和地堑地形中加入异常体，如图10所示.均匀空间的背景电阻率值分别为10Ωm，100Ωm.圆形异常体的电阻率分别为100Ωm，10Ωm，异常体中心位于(0，4000m)，半径1000m.

由于TE模式对各向异性以及起伏地形不敏感，为此只分析TM模式下的计算结果.根据起伏地形的研究可知，地垒地形导致TM模式视电阻率曲线表现出了低阻异常，地堑地形使TM模式的视电阻率曲线表现出了高阻异常，地垒地形中高阻和地堑地形中低阻异常的视电阻率计算结果如图11所示.从图中可以看出，地形对视电阻率的影响明显，异常体的特征几乎表现不出来.

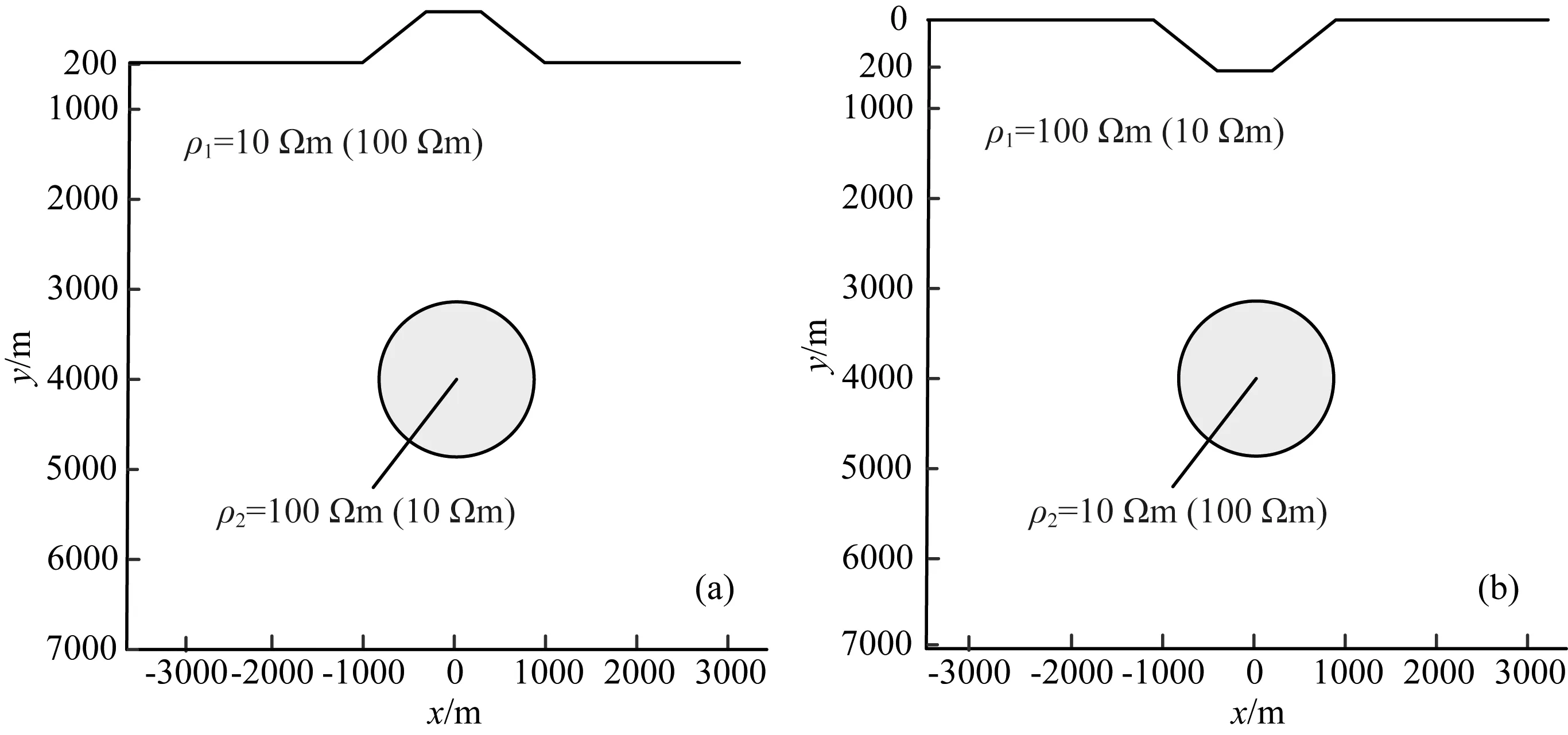
图10 起伏地形下含有异常体模型(a) 地垒中异常; (b) 地堑中异常.Fig.10 The model of abnormal body under undulating terrain(a) Anomaly body in horst; (b) Anomaly body in graben.

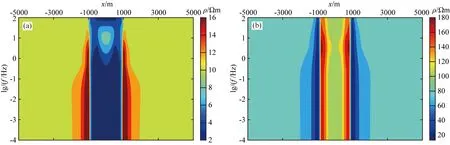
图11 起伏地形下含有异常体模型视电阻率模拟结果(a) 地垒中高阻; (b) 地堑中低阻.Fig.11 The result of abnormal body under undulating terrain(a) High resistivity in horst; (b) Low resistivity in graben.

为了研究起伏地形下不同各向异性系数异常体的电磁响应特征，将图10中的异常体改为各向异性体，选取受地形影响较小的200m的起伏地形作为研究对象.固定频率0.1Hz，保持平行电导率不变，改变垂直电导率的视电阻率计算结果如图12所示.固定垂直电导率，改变平行电导率的视电阻率计算结果如图13所示.从图12和图13中可以看出，地形对TM极化模式的影响要远大于各向异性本身的影响.当改变垂直电导率时，无论是低阻异常还是高阻异常，地形几乎掩盖了异常体的信息.当改变平行电导率时，TM极化模式对于地形下的低阻异常表现出了一定的分辨能力.

综合起伏地形下含有异常体的分析，可以得出：

(1) 地形对视电阻率的影响明显，导致异常体的特征几乎表现不出来.在数据处理中必须进行地形校正，提高异常的分辨率.

(2) 各向异性体的平行电导率影响要大于垂直电导率，当改变垂直电导率时，无论是低阻异常还是高阻异常，地形掩盖了异常体的信息.

(3) 对于低阻异常，尤其是平行电导率变化较大时，TM极化模式表现出了一定的分辨能力.大地电磁法对低阻异常体的探测能力比高阻异常体要强.

4 结论

本文基于复合二次径向基函数构造了无网格法形函数，推导了大地电磁无网格法等价线性方程组，研究了系数矩阵的压缩存储方法以及大型稀疏复线性方程组快速求解算法，实现了起伏地形下各向异性的2D大地电磁数值模拟.主要结论如下：

(1) 基于径向基函数插值的无网格法数据结构简单，形函数的构造只需节点信息，摆脱了网格限制，边界条件加载方便，层状模型与解析解的对比结果表明计算相对误差小于1%，该方法可以有效指导大地电磁数值响应计算;

(2) 起伏地形严重影响着电磁场的分布，很大程度上改变了原有的异常特征.地垒地形TM模式下的视电阻率呈现大低阻异常中夹小高阻异常的复杂现象，而地堑地形TM模式下视电阻率呈现大高阻异常中夹小低阻异常的复杂现象，相对而言地形对TE模式影响较小.随着高程的降低，地形对视电阻率和相位的影响逐渐降低.在数据解释时，需要对地形进行校正，消除地形导致的复杂假异常;

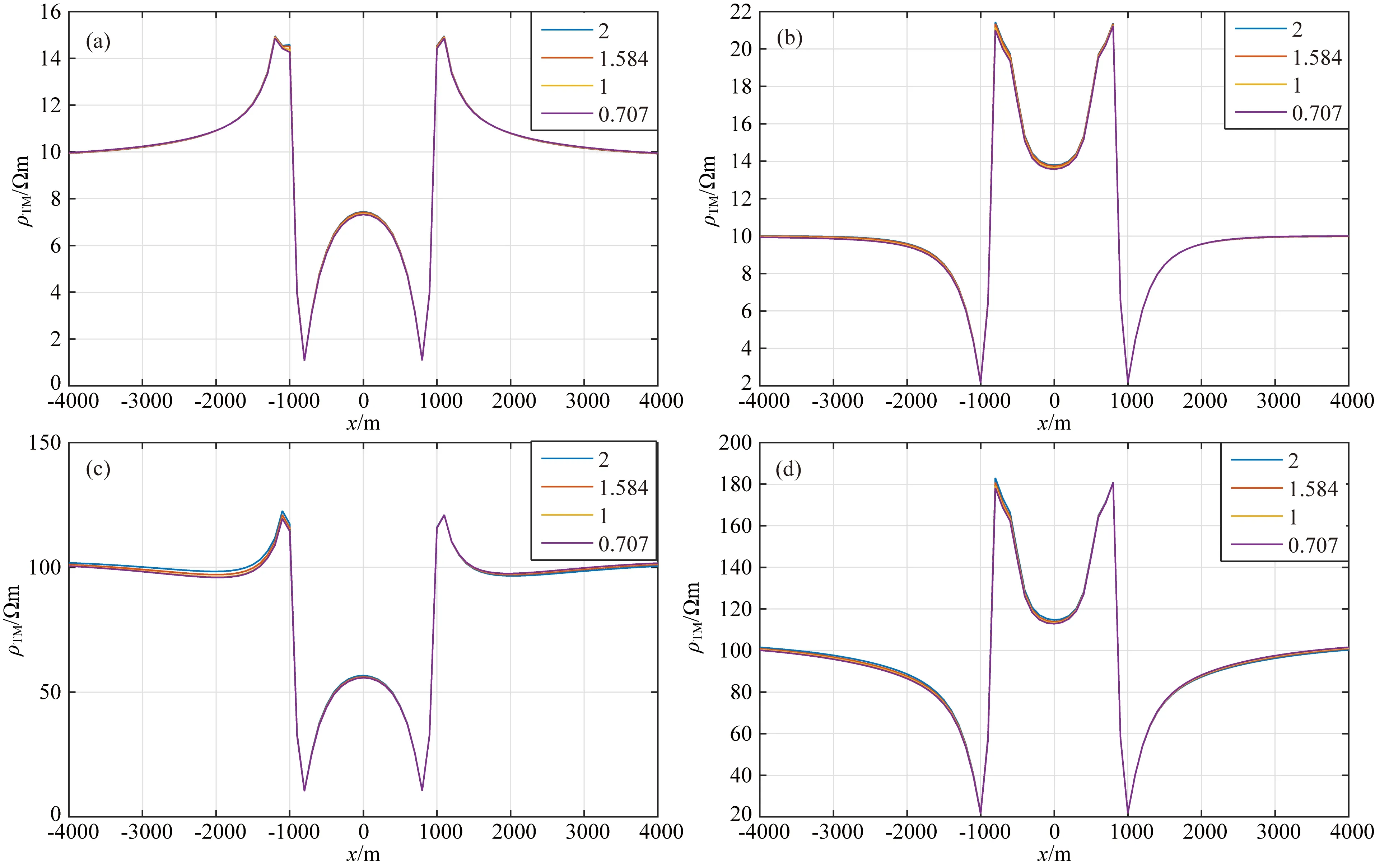
图12 改变垂直电导率不同各向异性系数下视电阻率计算结果(a) 地垒地形高阻异常; (b) 地堑地形高阻异常; (c) 地垒地形低阻异常; (d) 地堑地形低阻异常.Fig.12 The apparent resistivity result of different anisotropic coefficients by changing vertical conductivity(a) Horst terrain high resistivity anomaly; (b) Graben terrain high resistivity anomaly; (c) Horst terrain low resistivity anomaly; (d) Graben terrain low resistivity anomaly.

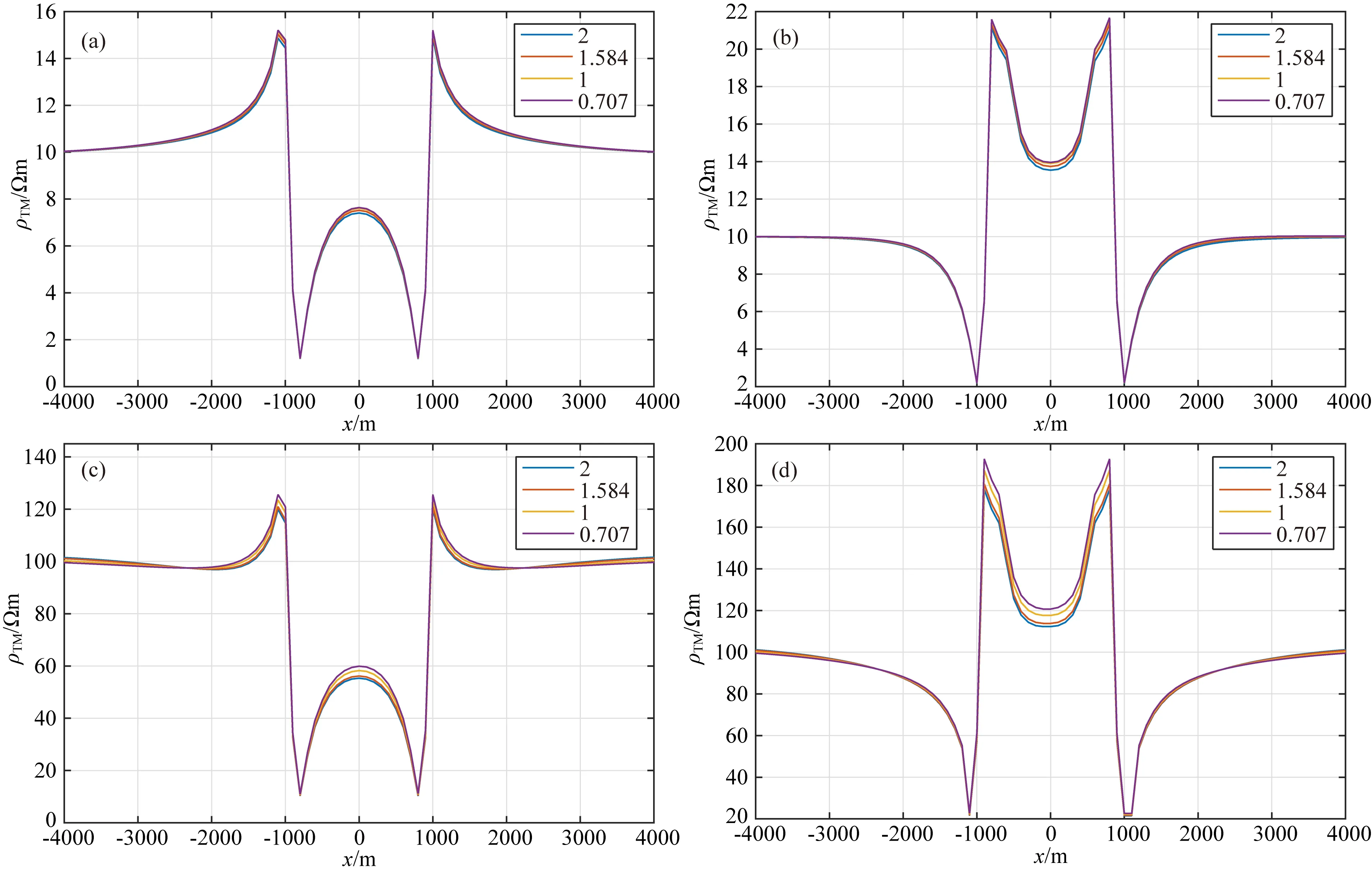
图13 改变平行电导率不同各向异性系数下视电阻率计算结果(a) 地垒地形高阻异常; (b) 地堑地形高阻异常; (c) 地垒地形低阻异常; (d) 地堑地形低阻异常.Fig.13 The apparent resistivity result of different anisotropic coefficients by changing parallel conductivity(a) Horst terrain high resistivity anomaly; (b) Graben terrain high resistivity anomaly; (c) Horst terrain low resistivity anomaly; (d) Graben terrain low resistivity anomaly.

(3) 当地下空间含有异常体时，地形对视电阻率的影响明显，导致异常体的特征几乎表现不出来.当改变异常体的各向异性系数时，地形也几乎掩盖了各向异性系数的影响.各向异性体的平行电导率影响要大于垂直电导率，在地垒和地堑地形下低阻异常在不同各向异性系数下具有一定的分辨能力.

作为一种新兴的引人注目的数值计算方法，无网格法有着自身的独特特点，在起伏地形和复杂介质的数值模拟上有着不可替代的优势，随着计算科学的快速发展，无网格法必将成为电磁法数值模拟的又一有效方法，为电磁法的高精度数值模拟开辟新的思路.

AtluriSN,ZhuT. 1998.AnewmeshlesslocalPetrov-Galerkin(MLPG)approachincomputationalmechanics.ComputationalMechanics, 22(2): 117-127.

ChengYM.2015.MeshlessMethod(Vol.1).Beijing:SciencePress.BelytschkoT,LuYY,GuL. 1994.Element-freeGalerkinmethods.InternationalJournalforNumericalMethodsinEngineering, 37(2): 229-256.BelytschkoT,KrongauzY,OrganD,etal. 1996.Meshlessmethods:Anoverviewandrecentdevelopments.ComputerMethodsinAppliedMechanicsandEngineering, 139(1-4): 3-47.DolbowJ,BelytschkoT. 1999.NumericalintegrationoftheGalerkinweakforminmeshfreemethods.ComputationalMechanics, 23(3): 219-230.FengDS,WangHH,DaiQW. 2013.Forwardsimulationofgroundpenetratingradarbasedontheelement-freeGalerkinmethod.ChineseJ.Geophys. (inChinese), 56(1): 298-308,doi:10.6038/cjg20130131.

HuoGP,HuXY,HuangYF,etal. 2015.MTmodelingfortwo-dimensionalanisotropicconductivitystructurewithtopographyandexamplesofcomparativeanalyses.ChineseJ.Geophys. (inChinese), 58(12): 4696-4708,doi: 10.6038/cjg20151230.

KeyK,WeissC. 2006.Adaptivefinite-elementmodelingusingunstructuredgrids:The2Dmagnetotelluricexample.Geophysics, 71(6):G291-G299.LiJJ,YanJB,HuangXY. 2015.Precisionofmeshfreemethodsandapplicationtoforwardmodelingoftwo-dimensionalelectromagneticsources.AppliedGeophysics, 12(4): 503-515.LiJJ,YanJB. 2015.Magnetotellurictwo-dimensionalforwardbyfiniteelement-radialpointinterpolationmethod.TheChineseJournalofNonferrousMetals, 25(5): 1314-1324.

LiYG,PekJ. 2008.Adaptivefiniteelementmodellingoftwo-dimensionalmagnetotelluricfieldsingeneralanisotropicmedia.GeophysicalJournalInternational, 175(3): 942-954.

LiJM.Geoelectricfieldandelectricalexploration.Beijing:GeologicalPublishingHouse.

LiuGR,GuYT. 2005.AnIntroductiontoMeshfreeMethodsandTheirProgramming.Netherlands:Springer.

LiuGR. 2010.MeshfreeMethods:MovingBeyondtheFiniteElementMethod.BocaRaton:CRCPress.

MackieRL,MaddenTR,WannamakerPE. 1993.Three-dimensionalmagnetotelluricmodelingusingdifferenceequations-theoryandcomparisonstointegralequationsolutions.Geophysics, 58(2): 215-226.NguyenVP,RabczukT,BordasS,etal. 2008.Meshlessmethods:Areviewandcomputerimplementationaspects.MathematicsandComputersinSimulation, 79(3): 763-813.PekJ,VernerT. 1997.Finite-differencemodellingofmagnetotelluricfieldsintwo-dimensionalanisotropicmedia.GeophysicalJournalInternational, 128(3): 505-521.PekJ,SantosFAM. 2002.Magnetotelluricimpedancesandparametricsensitivitiesfor1-Danisotropiclayeredmedia.Computers&Geosciences, 28(8): 939-950.

QinLJ,YangCF,ChenK. 2013.Quasi-analyticsolutionof2-Dmagnetotelluricfieldsonanaxiallyanisotropicinfinitefault.GeophysicalJournalInternational, 192(1): 67-74.

WittkeJ,TezkanB. 2014.Meshfreemagnetotelluricmodelling.

GeophysicalJournalInternational, 198(2): 1255-1268.

XuSZ.Finiteelementmethodingeophysics.Beijing:SciencePress.

ZhangJF，ZhiQQ，LiX，FengB.2013. 2.5Dfiniteelementnumericalsimulationforelectricdipolesourceonridgeterrain.ChineseJournalofNonferrousMetals, 23(9):2540-2550.

ZhadanovMS,VarentsovIM,WeaverJT,etal. 1997.MethodsformodellingelectromagneticfieldsresultsfromCOMMEMI-theinternationalprojectonthecomparisonofmodellingmethodsforelectromagneticinduction.JournalofAppliedGeophysics, 37(3-4): 133-271.

附中文参考文献

程玉民. 2015. 无网格方法(上册). 北京: 科学出版社.

冯德山, 王洪华, 戴前伟. 2013. 基于无单元Galerkin法探地雷达正演模拟. 地球物理学报, 56(1): 298-308,doi: 10.6038/cjg20130131.

霍光谱, 胡祥云, 黄一凡等. 2015. 带地形的大地电磁各向异性二维模拟及实例对比分析. 地球物理学报, 58(12): 4696-4708,doi: 10.6038/cjg20151230.

李俊杰, 严家斌. 2015. 大地电磁二维正演中的有限元-径向基点插值法. 中国有色金属学报, 25(5): 1314-1324.

李金铭. 2005. 地电场与电法勘探. 北京: 地质出版社.

柳建新, 蒋鹏飞, 童孝忠等. 2009. 不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用. 中南大学学报(自然科学版), 40(2): 484-491.

刘云, 王绪本. 2012. 电性参数分块连续变化二维MT有限元数值模拟. 地球物理学报, 55(6): 2079-2086,doi: 10.6038/j.issn.0001-5733.2012.06.029.

徐世浙. 1994. 地球物理中的有限单元法. 北京: 科学出版社.

张继锋, 智庆全, 李貅等. 2013. 起伏地形电偶源2.5维有限元数值模拟. 中国有色金属学报, 23(9): 2540-2550.

(本文编辑 刘少华)

2D anisotropic magnetotelluric numerical simulation using meshfree method under undulating terrain

JI Yan-Ju1,3, HUANG Ting-Zhe1, HUANG Wan-Yu1, LI Tong-Lin2, WANG Yuan1*

1CollegeofInstrumentationandElectricalEngineering,JilinUniversity,Changchun130026,China2CollegeofGeo-ExplorationScienceandTechnology,JilinUniversity,Changchun130026,China3KeyLaboratoryofGeo-ExplorationInstrumentation,MinistryofEducation,Changchun130026,China

As a kind of calculation method based on nodes, meshfree method is easy to construct the higher derivative and convenient to do adaptive analysis, it is especially suitable for the numerical simulation of complex models and complex medium structures. In view of the widespread existing problem that undulating terrain and anisotropic in the actual geophysical prospecting, we propose meshfree method to simulate the magnetotelluric response. The shape function is constructed by MQ-RBF function, the equivalent linear equations based on meshfree method is derived. We also study the compression and storage method of coefficient matrix and large sparse complex fast algorithm for solving linear equations, the 2D anisotropic magnetotelluric numerical simulation under undulating terrain is realized. The correctness of the algorithm is verified based on the layered model. The calculation results show that the relative error is less than 1% in both TM and TE mode; Through the simulation of horst and graben model, the influence rule of topography on the apparent resistivity and phase is obtained.We also study the numerical simulation of different anisotropic coefficients of horst and graben model, it establishes the theoretical basis for the study of electromagnetic field and the topographic correction of complex geological structure. With the rapid development of computational science, the meshfree method will surely become a new robust and high precision numerical method for electromagnetic field simulation.

Meshfree method; Radial point interpolation; Undulating terrain; Anisotropic; Magnetotelluric

10.6038/cjg20161211.

国家重大科研装备研制项目“深部资源探测核心装备研发”(ZDYZ2012-1)-05子项目资助.

嵇艳鞠，女，教授，博士生导师，主要从事电磁法理论及探测技术研究. E-mail: jiyj@jlu.edu.cn

*通讯作者 王远，男，讲师，博士，主要从事地球物理仪器研发及电磁法探测技术研究. E-mail: wangyuan_ciee @jlu.edu.cn

10.6038/cjg20161211

P631

2016-04-18，2016-06-16收修定稿

嵇艳鞠, 黄廷哲, 黄婉玉等. 2016. 起伏地形下各向异性的2D大地电磁无网格法数值模拟. 地球物理学报，59(12):4483-4493,

Ji Y J, Huang T Z, Huang W Y, et al. 2016. 2D anisotropic magnetotelluric numerical simulation using meshfree method under undulating terrain.ChineseJ.Geophys. (in Chinese),59(12):4483-4493,doi:10.6038/cjg20161211.