电流传输器模拟电感的设计及其在振动控制中的应用
柳维玮,毛崎波
(南昌航空大学飞行器工程学院,江西南昌,330063)
电流传输器模拟电感的设计及其在振动控制中的应用
柳维玮,毛崎波
(南昌航空大学飞行器工程学院,江西南昌,330063)
通过电流型运算放大器组成第二代电流传输器与RC元件实现模拟电路的设计,由此搭建压电分流阻尼系统控制机械结构振动。通过软件仿真测试模拟电感电路设计的正确性,并以根部粘贴压电陶瓷片的固支梁结构为例,对该结构的第三阶模态振动控制进行了实验研究和分析,结果表明:所设计的新型压电分流电路具有良好的减振效果。
第二代电流传输器;模拟电感;仿真;压电分流电路
0 引言
对于大电感值的无源电感体积庞大的问题,现普遍的做法是运用有源器件模拟电感来解决。第二代电流传输器(CCⅡ)具有电流变换的功能以及较宽的频率范围和动态范围,在阻抗变换、有源滤波、正弦振荡器等方面得到广泛应用。用第二代电流传输器模拟电感相对电压型集成运算放大器模拟电感是一种新的设计方法,有利于模拟电感性能的提高和进一步集成化。
压电分流阻尼技术的基本思路是利用压电材料的正压电效应,将结构振动的机械能转化为电能,再通过外接电路将电能转化为热能被电阻元件消耗,从而起到抑制结构振动作用。而在控制低频振动的分流电路设计中通常需要较大的电感,才能达到较好的控制振动目的。
本文应用第二代电流传输器实现压电分流阻尼电路的模拟电感设计,通过Multisim软件仿真验证模拟电感设计的正确性,并通过实验把所设计的模拟电感应用于控制结构振动的分流阻尼电路中。
1 电路设计
第二代电流传输器是三端口器件,其符号如图1所示。其电压电流输入输出特性用矩阵表示为:

图1 CCⅡ符号

1.1CCⅡ模拟电感的设计
图2是CCⅡ模拟电感设计的电路原理图

图2 模拟电感原理图
结合图2和(1)式,可以写得:

式中:

输入电流可表示为:

联立(2)式与(3)式,化得:

从而,

式中等效电感为:

1.2带电阻补偿的CCⅡ模拟电感的设计
在图2所示电路上加入一级负阻抗转换器,重新设计带电阻补偿的接地模拟电感,如图3所示。
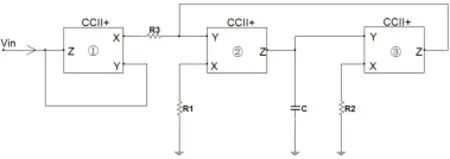
图3 带电阻补偿的CCⅡ模拟电感原理图
结合图3和(1)式,输入电压可表示为:

同理,图3的输入电流可表示为:
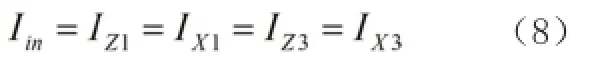
式中:

由式(8)可得:

结合式(7)和(9)可得图3所示电路的阻抗为:

从式(10)可知,该电路的等效电感和等效电阻分别为:
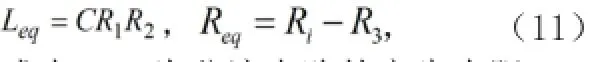
式中,Ri为分流电路的寄生内阻。
从式(11)可以发现,该压电分流电路的主要优点在于可以独立调节所需的等效电感值和等效电阻值。
2 模拟电感的软件仿真

(b)模拟电感的RLC电路仿真结果
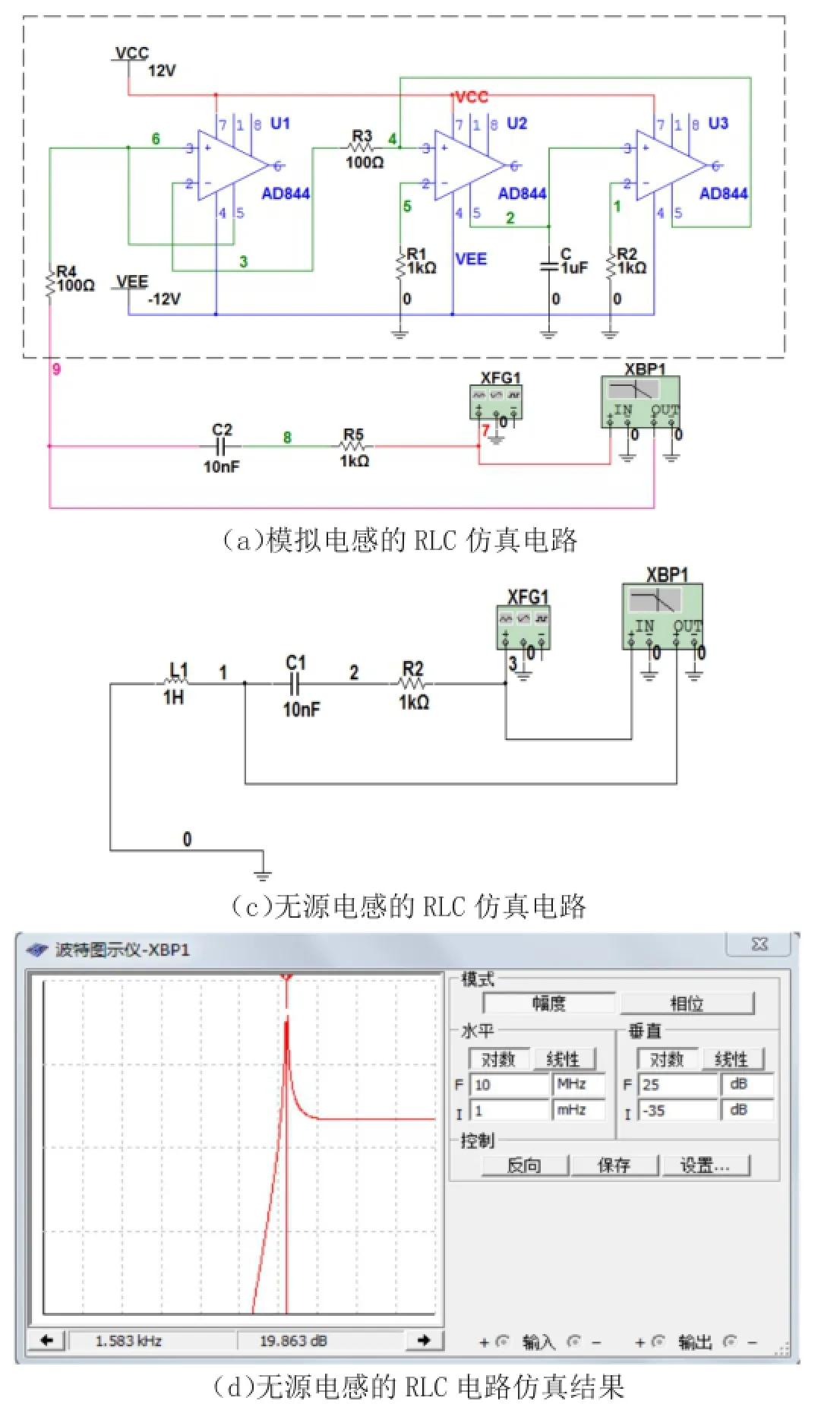
图4 Multisim仿真图片
针对带电阻补偿的CCⅡ模拟电感的电路设计运用Multisim进行软件仿真。采用商用电流型集成运算放大器AD844实现电流传输器,在此基础上如图3的原理图搭建模拟电感。图4(a)是由模拟电感组成的RLC电路,其中虚线框内为模拟电感,假设模拟电感串联一个100Ω的内阻,正好由-100Ω的补偿电阻抵消为一个纯电感,将其电路与图4 (c)无源电感组成的RLC电路对比。通过波特图示仪观察两者的幅频特性曲线,模拟电感的RLC电路与无源电感的RLC电路上升峰值分别为19.909dB和19.863dB,其峰值频率分别为1.588kHz和1.583kHz,两条曲线形状也完全吻合,由此验证了所设计的模拟电感的正确性。
3 振动实验研究
针对本文采用的分流电路,可将分流电路模拟为一个等效电阻Req和一个等效电感Leq串联的电路。由于本文主要目的是通过实验验证运用第二代电流传输器所设计的模拟电感在压电分流技术中的可行性,对于分流电路中的电感和电阻最优值不做详细推导。由文献[5-7]可知,最佳等效电感值Lopt和等效电阻值Ropt分别为 :
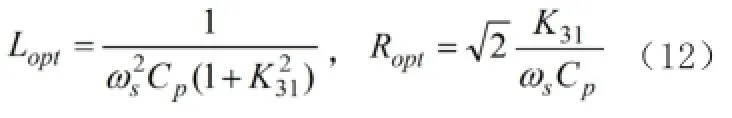
4 结束语
第二代电流传输器模拟电感,解决了电路设计中电感量值与体积之间的矛盾。仿真模拟电感电路与物理无源器件组成的电路特性基本相同,这为压电分流阻尼电路提供了一种新的设计方法。通过实验验证了所设计的电路抑制振动效果良好。可见,第二代电流传输器模拟电感能够广泛应用于工程实践当中。
本实验采用两端固支的6061铝合金梁,该梁的尺寸为580mm×30mm×3.5mm。选择两片P-5H型的压电陶瓷片(PZT)对位粘贴在梁的根部,粘贴于梁下表面的陶瓷片作为激振源,而粘贴于梁上表面的陶瓷片作为与分流电路相连实现压电分流阻尼系统。使用CA-YD-107型号加速度传感器来测试固支梁的振动情况,并选用江苏泰斯特电子设备制造有限公司的TST5912动态信号测试分析仪进行振动分析。实验图片如图5所示。

根据上述参数在面包板上搭建了压电分流电路。选用AD844电流型集成运算放大器实现第二代电流传输器,由图3带电阻补偿的CCⅡ模拟电感原理图搭建模拟电感,并选择, ,。然后搭建RLC串联压电分流阻尼电路,其压电分流阻尼系统中的压电陶瓷所带电容相当与RLC串联电路中的电容,然而电阻的理论最优值与实际最优值有较大误差,所以采用在线调节的方式得到RLC串联电路中实际最佳电阻值。
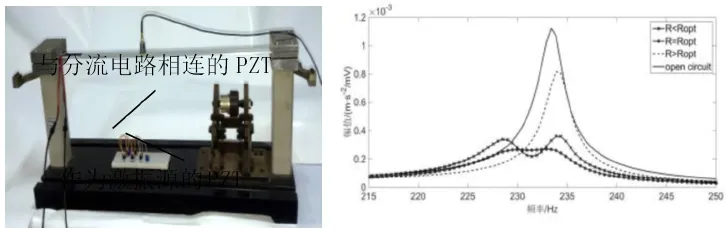
图5 实验图片
针对第三阶模态,将电路设置为最佳参数后,选择扫频激励方式,分别将最佳等效电阻值调节增大5%和减小5%,对梁的振动进行振动信号采集分析。图5表示在最佳等效电感值(3.55H)时,不同等效电阻值下振动信号与激励信号的传递函数图。可以发现当等效电阻值小于最佳值时,控制频率处的尖峰有明显下降,并且在两侧产生尖峰。而在等效电阻值大于最佳值时,控制效果会随之下降。并从图可以看出,当选取最佳等效电感值及最佳等效电阻值时,所设计的压电分流阻尼电路具有良好的抑制振动的效果。
[1] 贺富堂.模拟电感的实现及其应用[J].高校实验室工作研究,2014(2):30-32.
[2] 宋爱军,吴阿林.一种基于电流传送器的正弦波振荡器[J].仪表技术,2002(5):30-48.
[3] 毛崎波.通过压电分流阻尼技术抑制结构振动的实验研究[J].中国机械工程,2011,22(22):2690-2693.
[4] 马小陆,裘进浩,季宏丽,等.负电容在主-被动混合压电振动控制中的应用[J].华南理工大学学报,2012,40(3):112-118.
[5] CARUSO G. A critical analysis of electric shunt circuits employed in piezoelectric passive vibration damping [J]. Smart Materials and Structures, 2001, 10(5): 1059–1068.
[6] MAO Qibo, PIETRZKO S. Control of noise and structural vibration - A MATLAB based approach [M]. London:Springer, 2013:325-366.
[7] PIETRZKO S, MAO Qibo. Reduction of structural sound radiation and vibration using shunt piezoelectric materials [J]. Solid State Phenomena, 2009, 147:882-889.
Design of inductance simulators based on current conveyor and its application to Vibration Control
Liu Weiwei,Mao Qibo (School of Aircraft Engineering,Nanchang Hangkong University,JiangXi Nanchang,330063)
Design of inductance simulators using second-generation current conveyor and RC components, and second-generation current conveyor composed of current-mode operational amplifier.From this design to set up piezoelectric shunt damping system to control mechanical structure vibration.Through software simulation test the correctness of the simulation inductance circuit design.Furthermore,with an example of clamped-clamped beam bonded piezoelectric patch, the third natural frequency of the beam is targeted to be controlled,and the experiment research is performed. The experimental results show that the design of new type piezoelectric shunt circuit has good vibration damping effect.
second-generation current conveyor(CCⅡ); inductance simulators;simulation;piezoelectric shunt circuit

