开式转子发动机计算模型及调节研究

屠秋野，倪力伟，杨祥明，郑恒，蒋平

（1.西北工业大学动力与能源学院，西安710072；2.中国航发商用航空发动机有限责任公司，上海200241）

开式转子发动机计算模型及调节研究

屠秋野1，倪力伟1，杨祥明1，郑恒2，蒋平2

（1.西北工业大学动力与能源学院，西安710072；2.中国航发商用航空发动机有限责任公司，上海200241）

目前先进的开式转子发动机多采用变桨距、双排共轴对转桨作为推进部件。采用双排桨的气动计算方法，根据单排桨特性图计算对应的双排对转桨特性图，验证对转桨性能计算模型。在双轴涡轮喷气发动机计算模型的基础上，添加动力涡轮、行星差动齿轮和双排对转桨，组成开式转子发动机计算模型。采用该模型研究了开式转子发动机的调节计划，对比了等转速和等叶尖速度调节的不同，以及对开式转子发动机高度速度特性的影响，并使用美国PRO O SIS模型对计算结果进行验证。结果表明：开式转子发动机模型计算精度较高，可较准确地研究不同设计参数和调节规律下发动机的总体性能，其中固定桨扇叶尖速度的调节计划在较低飞行速度下具有高推力、低油耗的优点，可以获得较好的全包线性能。

开式转子发动机；对转桨；动力涡轮；行星差动齿轮；调节计划；总体性能

0 引言

开式转子发动机综合了涡桨发动机耗油率低和涡扇发动机飞行速度高的优点，可用作最大马赫数0.80左右的民用客机和军用运输机的动力装置。20世纪70年代的能源危机，使航空领域的研究人员更加注重航空器的经济性，美国提出并验证了采用高速螺旋桨的开式转子发动机方案。20世纪80年代起，美国对高转速、高飞行速度的桨扇发动机进行了大量研究和测试，其中包括NASA实施的单排涡扇技术计划。该计划对一系列不同几何模型进行了风洞测试，研究了其性能和声学特性，表明桨扇发动机比涡扇发动机可以节省15%～40%的燃油，且扭转叶片可以在马赫数0.8的巡航条件下达到80%的净效率并能显著减小噪声[1]。在21世纪初，NASA开展了1项亚声速固定翼航空器(SFW)项目，旨在刺激相关技术发展并降低航空器对环境的影响，提出了其后十几年内发动机的排放、噪声和油耗的研制目标[2]。为了评估先进推进技术是否满足该目标，SFW系统分析团队在1个先进单通道飞机(ASAT)上测试了新型推进系统的潜在环境优势，评估了2种超高涵道比涡扇(UHB)概念[3]，认为其相对20世纪90年代的技术水平可使油耗降低29%的、使起降过程氮氧化合物排放减少50%，最大噪声降低25EPNdB。时至今日，开式转子发动机的理论和试验技术的发展已经趋于成熟，且开式转子也被认为是未来民用航空发动机的1个主要发展方向。

本文以开式转子发动机为研究对象，研究了双排对转桨的性能计算方法，用该计算方法计算了对转桨特性图并进行了对比验证。在双轴发动机计算模型的基础上建立了开式转子发动机整机性能计算模型，研究了开式转子发动机的调节计划。为发动机设计和调节计划的选取提供理论依据。

1 先进开式转子部件技术特点

传统螺旋桨在巡航马赫数高于0.6时效率迅速降低。美国于1975年首先提出高速螺旋桨的构思，减小桨径以降低桨尖的切向速度，增加桨叶数和实度以吸收发动机巨大功率，同时减薄桨叶厚度，采用后掠或前掠形式来减缓空气压缩性影响。这种高速螺旋桨即开式转子发动机推进方式的主要特点。

早期的航空螺旋桨都为定距桨，只能在特定工作状态下保持高性能。随着活叶桨和变距桨的发明，螺旋桨的工作状态不断得到改进。目前国内外研究的先进开式转子发动机采用的螺旋桨均为变距桨，即调节桨距角使螺旋桨在不同工作状态下都保持较高的效率。

在开式转子发动机发展的初期，针对单级螺旋桨桨叶气动涡流和功率吸收有限的问题，研究人员提出了双排共轴对转桨的概念，即1对螺旋桨绕同一根轴旋转，旋转方向相反。1982年，NASA发表了多篇关于对转桨概念的报告[4-5]，系统地阐述了对转桨的优点。这些优点可以简单表述为：（1）发动机传到飞机的反作用力矩近似为零，可以省去很多力矩平衡措施；（2）在高速飞行状态下，总叶数相等的共轴桨的总效率比非共轴桨的更高；（3）对于大功率的发动机，共轴桨的起飞性能比单级桨的更好。基于这些优点，现代的开式转子发动机均采用双排对转桨作为主要推进部件。

2 桨扇部件性能模型

2.1 传统单排桨性能模型

螺旋桨的气动计算常用理论包括螺旋桨动量理论、理想螺旋桨理论、螺旋桨叶素理论和涡流理论等。根据螺旋桨的叶素理论，可得螺旋桨的性能计算公式[6]

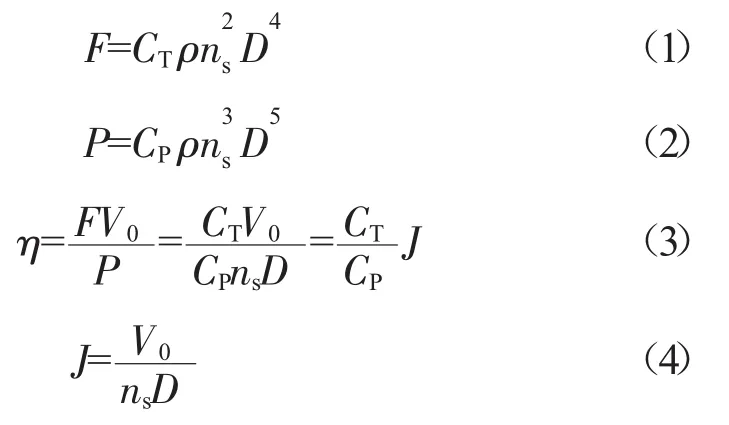
式中：F为螺旋桨拉力；P为螺旋桨消耗功率；ρ为空气密度；ns为螺旋桨转速；D为螺旋桨直径；V0为飞行速度；CT为桨的拉力系数；CP为桨的功率系数；η为桨的推进效率；J为桨的进距比。其中，拉力系数CT和功率系数CP可以看作进距比J和安装角β的函数。

2.2 螺旋桨的特性曲线表示

螺旋桨特性曲线指通过风洞的试验数据绘制而成的拉力特性CT（J）、功率特性CP（J）和效率特性η（J）曲线。式（3）表明，在飞行速度不为零的条件下，3条特性曲线只需已知其中2条即可计算出第3条。

主要利用螺旋桨的相似性理论获得螺旋桨特性曲线。在风洞试验中，为了满足相似条件，理论上需要满足螺旋桨工作的几何相似、运动相似和动力相似。而在实际操作中，由于模型和原型桨采用相同的介质空气，同时满足各相似准则较为困难。一般在缩比模型的风洞试验中，在满足几何相似之后，还要求模型和原型满足进距比J和马赫数Ma相等，从而得到原型的CT和CP，而对雷诺数(Re，表示惯性力和黏性力的比值)和弗劳德数(Fr，表示惯性力和重力的比值)不作过多要求。

桨叶数相同、翼型相同但直径不同的螺旋桨可以用同一特性图来表示不同安装角和飞行条件下的螺旋桨特性。不同轮毂比的螺旋桨，其沿工作区域分布的气流入射角和力的分配并不相同，因此1张螺旋桨特性图只适用于特定的轮毂比。但通过将CP和CT替换为修正功率系数CPQA和修正拉力系数CTQA，可以满足轮毂比变化时拉力和功率的1阶近似。修正后的系数定义为

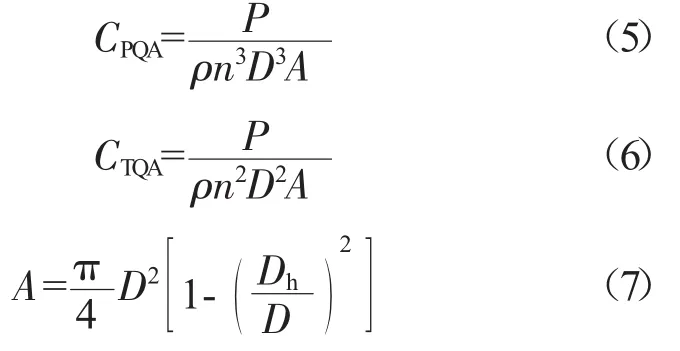
式中：A为螺旋桨的空气流通面积；Dh为螺旋桨轮毂直径；D为螺旋桨直径。

目前公开发表的资料中，缺少完整连续的高速桨特性图。NACA在1954年发表的螺旋桨气动分析报告中给出了某型传统螺旋桨在较大范围内的工作特性图[7]。通过将该特性图按高速桨特性图调整数值进行修正，可以得到用于近似计算的全包线单级桨特性图，如图1所示。

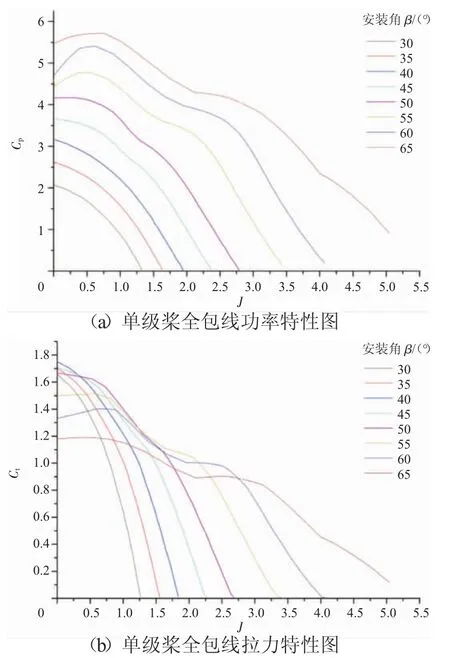
图1 单级桨全包线特性

传统的单级螺旋桨特性图也可以用来表示双级对转桨的特性。定义双排桨的CT和CP如下

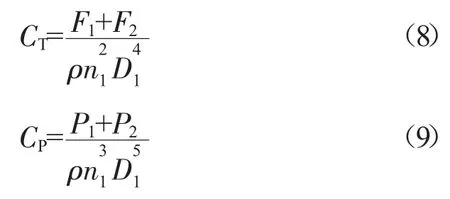
式中：F1、F2分别为前后排桨产生的拉力；P1、P2分别为前后排桨消耗的功率；n1为前排桨的转速；D1为前排桨的直径。在实际使用时，直接给出按前排安装角β1变化的对转桨特性图，其中β1和β2的关系与前后排桨径比、转速比和功率分配一起作为隐藏参数，不体现在特性图中，从而得出的特性图与单级桨特性图相似。

2.3 双级对转开式转子特性计算

本文采用前后级分开独立计算的方法处理双排对转桨的特性。在已知前后级各自单级特性的基础上，考虑前排桨对后排桨的影响，将前后排安装角、前后桨径比、转速比等作为已知条件，分别计算前后排桨的性能参数。计算时，前排桨按照传统单级桨性能计算方法进行计算，将后排桨的旋流速度看作后排桨额外的转速，并转换为只有轴向速度的假想来流条件，从而对后排桨用同样的单排桨特性图进行计算[8]。

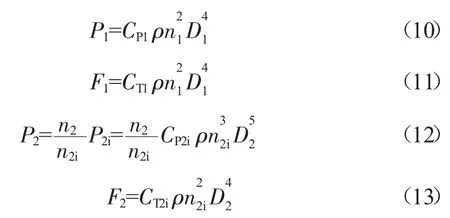
式中：CP1、CT1为前排桨的功率系数和拉力系数；n2为后排桨的转速；D2为后排桨的直径；n2i为后排桨假想状态转速；CP2i、CT2i为后排桨假想状态下特性图上查出的功率系数和拉力系数。具体的推导和计算过程见文献[9]。

采用2.2节给出的单级桨特性图（图1），选取F-7/A-7的对转桨模型对上面介绍的对转桨特性计算方法[9]进行了对比验证。F-7/A-7对转桨模型尺寸数据[10]见表1，前后排桨转速相同。

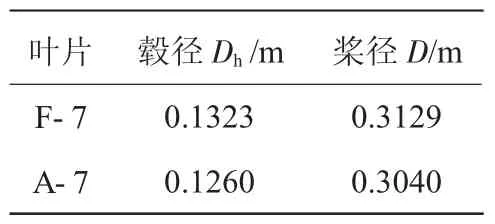
表1 对转桨模型尺寸

已知飞行状态和前后排桨的尺寸，在给定前后排桨的安装角和转速后，可以分别计算得到前后排桨的拉力F1、F2和功率P1、P2，加之前排桨的转速和桨径已知，利用式（8）、（9）可以计算对转桨的CT和CP。

对不同的前后排桨的安装角和转速，计算不同进距比下对转桨的CP，并与文献[8]中试验得出的对转桨特性图进行对比，结果如图2所示。通过4组不同前后排安装角的特性曲线对比结果可见，采用简化的对转桨气动计算方法可以较好地表现前后排安装角或进距比变化时的对转桨特性。只有在进距比较大时，简化模型的计算结果才与试验值之间存在较大偏差。

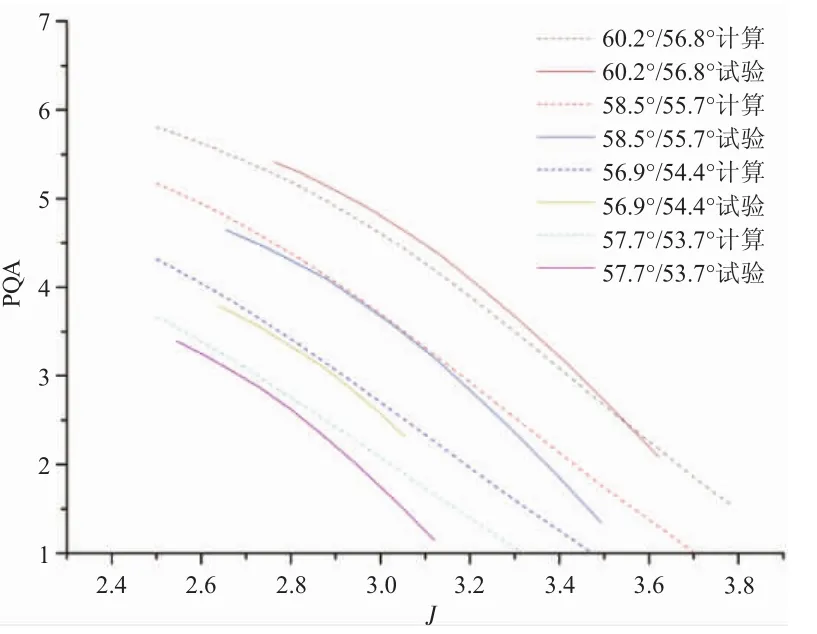
图2 双级对转桨特性计算验证

GE36开式转子发动机结构如图3所示。GE36发动机在结构上可分为燃气发生器和推进器2部分。其中，燃气发生器为F404核心机，推进部件包括由对转涡轮作为动力涡轮提供功率的对转桨和发动机的尾喷管。本文采用的开式转子发动机结构与该图相近。

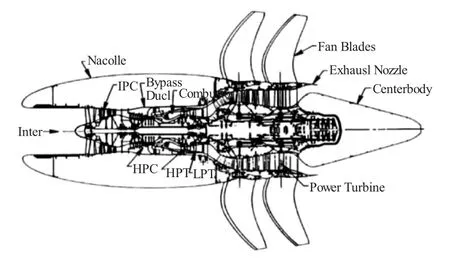
图3 GE 36对转开式转子发动机[10]

开式转子发动机模型结构如图4所示。航空发动机模型的气动热力计算按发动机中气体流经的部件顺序进行。

图4 开式转子发动机部件结构

在部件模型中，有必要对齿轮传动部件的模型进行特殊说明。

3.2 对转开式转子传动结构

对转桨的旋转轴相同，但旋转方向相反，因此不能由普通的动力涡轮直接驱动。双排对转桨常用的驱动方式有2种：一是由对转涡轮直接驱动，二是通过齿轮结构将非对转涡轮的转速和功率分配到双排对转桨上。

直接由对转涡轮驱动可以省去复杂的齿轮结构，减少齿轮处机械损失，降低结构复杂性，提高发动机稳定性，同时发动机质量较轻，有利于提高发动机的性能参数；与对转涡轮相比，采用齿轮传动技术更为成熟，且转速比较容易控制，可以采用较高转速的涡轮，利于设计高功率的开式转子部件。

在开式转子发动机发展过程中，曾大量采用对转涡轮直接驱动的模型。但现代开式转子要求的吸收功率较高，为了提供足够的功率，对动力涡轮转速的要求也较高；开式转子的转速受到桨的尺寸和叶尖马赫数的限制，其相对较低的转速使得对转涡轮的设计较为困难。为了满足功率要求，需要提高对转涡轮的级数，由此产生的对转涡轮质量尺寸增加超过了齿轮结构对发动机性能的影响。因此，目前齿轮传动方案在开式转子发动机的结构设计中更为常见[12]。

本文开发的模型主要针对行星齿轮结构。在行星齿轮结构中，动力涡轮与对转桨之间的传动结构需要将1个转轴的功率分配到另外2个转速相反的轴上[13]，较为常用的齿轮结构是2自由度的行星差动齿轮结构，如图5所示。

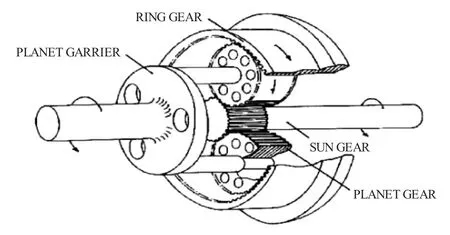
图5 行星差动齿轮结构

关于行星差动齿轮结构在开式转子结构中应用的详细描述见文献[13]。2自由度的行星差动齿轮与传统的双轴齿轮结构的区别在于：（1）传统双轴齿轮有1个输入轴和1个输出轴，而行星差动齿轮可能有1个输入轴和2个输出轴或是2个输入轴和1个输出轴；（2）传统双轴齿轮有1个固定的转速传动比，在所有工作状态下均保持不变，且决定了各轴的功率分配。而2自由度的行星差动齿轮有固定的扭矩比，在不同工作状态下，每个轴的转速根据功率平衡和扭矩比确定，即行星齿轮传动机构的功率分配由扭矩比决定。行星差动齿轮的功率分配不同于传统的单向减速装置，必须根据其自身结构特点进行分析。2自由度的行星差动齿轮结构通过太阳轴、齿圈和行星架3个部件进行转速和功率的输入输出，该齿轮结构的部分计算如下[14]

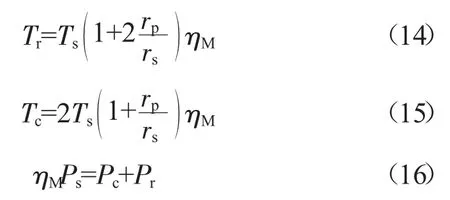
式中：Tc、Tr和Ts分别为通过行星架、齿圈、太阳轴输入输出的扭矩；Pc、Pr和Ps分别为行星架、齿圈、太阳轴的功率；rp/rs为行星齿轮与太阳轮的半径比；ηM为齿轮结构的机械效率。行星差动齿轮计算公式的详细推导见文献[14]。

3.3 对转开式转子整机模型及验证

本文的对转开式转子发动机整机模型是在描述燃气发生器共同工作的数学模型的基础上建立的。由于增加了动力涡轮和齿轮部件，所以整机模型增加了4个初猜值，分别为动力涡轮的相对转速nPT、动力涡轮特性图βPT值、前后排桨扇特性的βP1和βP2值，相应地补充动力涡轮和桨扇部件的共同工作方程如下：

动力涡轮进口流量平衡

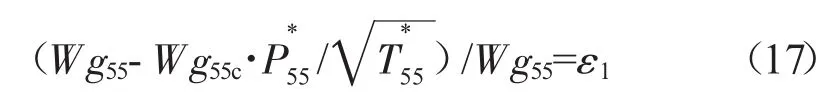
动力涡轮和桨扇部件功率平衡

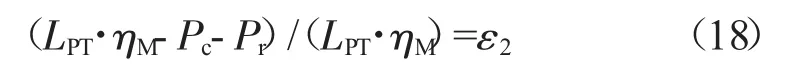
前排桨与行星轴扭矩平衡

后排桨与齿圈扭矩平衡

式中：Wg55为动力涡轮进口流量；Wg55c为由动力涡轮特性图得出的工作点换算流量和分别为高压涡轮进口处的总压和总温；LPT为动力涡轮功率；T1和T2分别为前后排桨的扭矩。

采用上述模型对行星差动齿轮传动的对转开式转子发动机性能进行了数值模拟。本文模拟的发动机结构包含1个双轴的燃气发生器，通过1个非对转动力涡轮经过行星差动齿轮驱动对转桨扇部件。

文中采用的开式转子发动机设计点参数取自文献[9]。发动机设计点选在巡航状态，高度H=11 km，马赫数Ma=0.72，大气温度ΔTISA=15 K。部分设计点参数见表2。

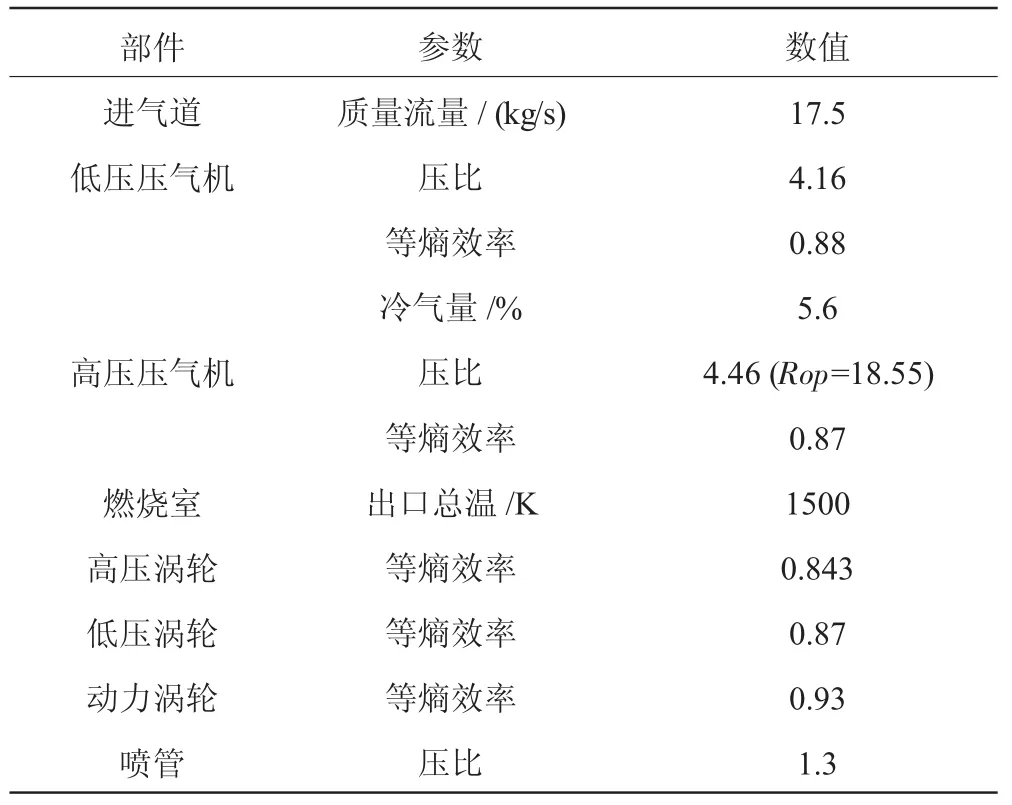
表2 设计点循环参数

在以上设计点工作条件下，按照前文的双排桨气动计算方法计算双排对转开式转子部件时，还需给定行星差动齿轮和桨扇部件的部分参数，具体参数见表3。

表3 桨扇部件设计点计算已知参数

在设计点，对转桨前后排桨转速相同，前排桨分配的功率更大。已知飞行状态和前排桨进距比，给定桨的安装角即可确定工作点在特性图上的位置，可以保证桨在设计状态具有较高的工作效率。给定桨扇进距比还可以计算叶尖相对马赫数，便于确定设计点桨叶的工作状态。

根据上述已知条件以及前文建立的开式转子发动机设计点模型，计算得到开式转子部件的其它参数，见表4。

文献[9]给出了通过PROOSIS模型[15]计算得到的在发动机该设计点下的性能参数。本文的计算结果与文献中结果的对比见表5。

从表中可见，本文的设计点计算结果与文献基本一致。计算结果表明，开式转子发动机的主要推力来源是双排桨，喷管排气推力所占比重较少。对比表3、5中的结果可知，F1/F2＜Pc/Pr，即后排桨的推进效率高于前排桨的，所以对转排列的双排桨有利于桨推进效率的提高。

表4 开式转子部件参数

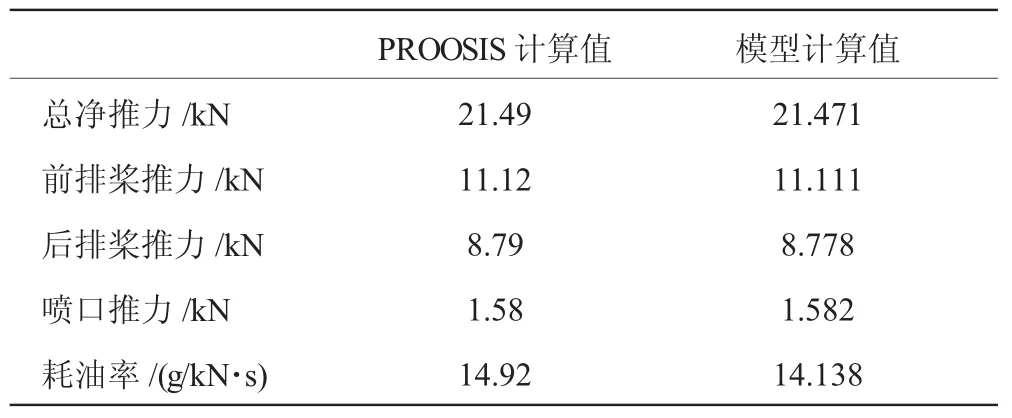
表5 发动机性能参数

4 开式转子发动机调节计划

为了在不同工作状态下达到最佳的工作状态，会针对不同的飞行状态采取不同的调节计划。开式转子发动机包括开式转子部件和燃气发生器。双轴燃气发生器常见的调节计划包括：保持低压转子转速不变、保持高压转子转速不变和保持燃烧室出口温度不变等。为了保证燃气涡轮的最大功率输出，本文选择控制燃烧室出口总温不变来调节燃气发生器的非设计性能。如果有具体的发动机工作参数限制，燃气发生器的调节计划还可以进一步完善。

4.1 桨扇部件调节计划

对于带自由涡轮的开式转子发动机，自由涡轮与桨通过传动机构相连，其转速与桨的转速直接相关。因此这种发动机除了燃气发生器的供油量外，常选取开式转子部件的安装角作为调节量。开式转子部件的调节计划有2种常见模式：一是根据变桨距螺旋桨发动机的控制经验，采用定转速的调节计划，利于保证涡轮工作高效稳定；二是桨叶安装角随飞行马赫数变化[16]。通过在不同飞行状态下考察不同安装角下桨扇的工作状态来确定安装角调节计划，更易于评估飞行包线内发动机的性能表现。

在桨叶安装角随飞行马赫数变化的调节计划中，在飞行过程中前排桨安装角设定为马赫数的函数。这种调节计划要求根据飞行状态改变安装角和燃油流量，以达到要求的推力指标。但由于该调节计划中安装角为马赫数的函数，在发动机推力要求发生变化时，桨和动力涡轮的转速会发生较大变化。因此，在开式转子发动机模型中，可以采用定叶尖速度的调节计划，兼顾推力要求和涡轮与桨的工作稳定性。在固定叶尖气流速度的调节计划中，由于桨扇安装角的变化范围有限，在部分工作条件下无法达到叶尖速度要求，此时以安装角限制为先。

基于上述分析，采用固定前后排叶尖速度的调节计划，计算得到开式转子发动机的不同马赫数下前排安装角随燃烧室出口总温T4的变化，如图6所示。其中，安装角最小值限制设定为30°。在相同马赫数下，随着供油量的增加，燃烧室出口温度升高，对应的安装角增大，提高桨的功率系数，从而使叶尖转速保持不变。对比安装角为马赫数函数的调节计划可以看出，固定叶尖速度的调节计划在给定马赫数时，不同的涡轮前温度对应的安装角不同。

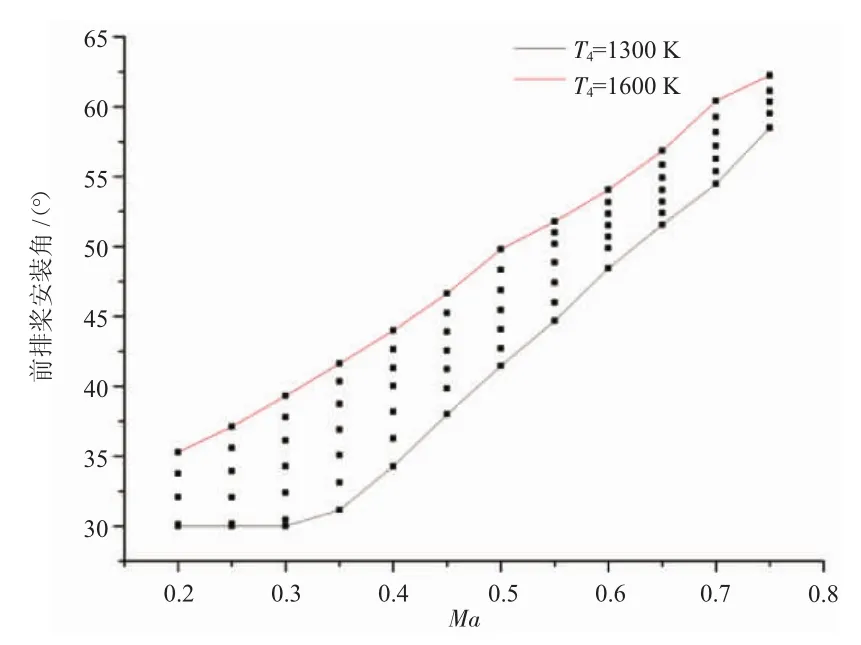
图6 固定叶尖速度调节下前后排安装角变化

4.2 不同调节计划高度速度特性

在给定的大气条件下，假定发动机在整个飞行包线内采取相同的调节计划。其中，燃气发生器的调节计划选择燃烧室出口总温T4=1500 K；开式转子部件的调节计划选择2种方案：固定前后排桨转速和固定前后排桨尖速度。采用本文开发的模型分别计算不同调节计划下的开式转子发动机高度速度特性，如图7～10所示。

固定转速调节下推力和耗油率随高度速度的变化如图7、8所示。从图中可见，在相同高度下，随着马赫数的增大，发动机推力减小，耗油率升高。这是由于在桨扇转速不变的情况下，随着飞行速度的提高，桨扇的进距比增大，拉力系数减小，因而桨扇部件的推力减小；同时桨的效率降低，使得耗油率升高。在相同马赫数下，发动机推力和耗油率均随着高度升高而减小。原因是高度增加导致大气密度降低，发动机进口的空气流量减少，燃气发生器的有效功减小，动力涡轮提供的功率降低，且桨的推力与空气密度成正比。主要有2方面的原因对耗油率造成影响：一方面，在11 km以下，随着高度增加，发动机进口温度和压力降低，循环的放热量减少；另一方面，燃气发生器换算转速增加带来的出口温度升高不能完全抵消发动机进口温度降低的影响，造成燃烧室进口总温降低，而燃烧室出口总温不变，所以循环的加热量增加。以上2个原因共同作用使燃气发生器的热效率提高，最终减小了发动机的耗油率。

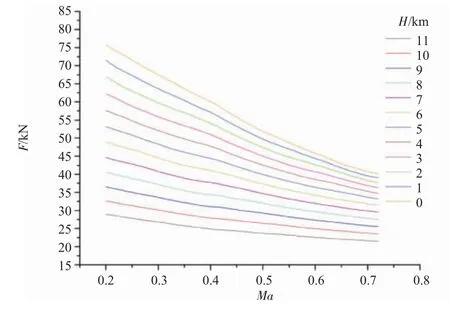
图7 固定转速调节下推力随高度速度的变化

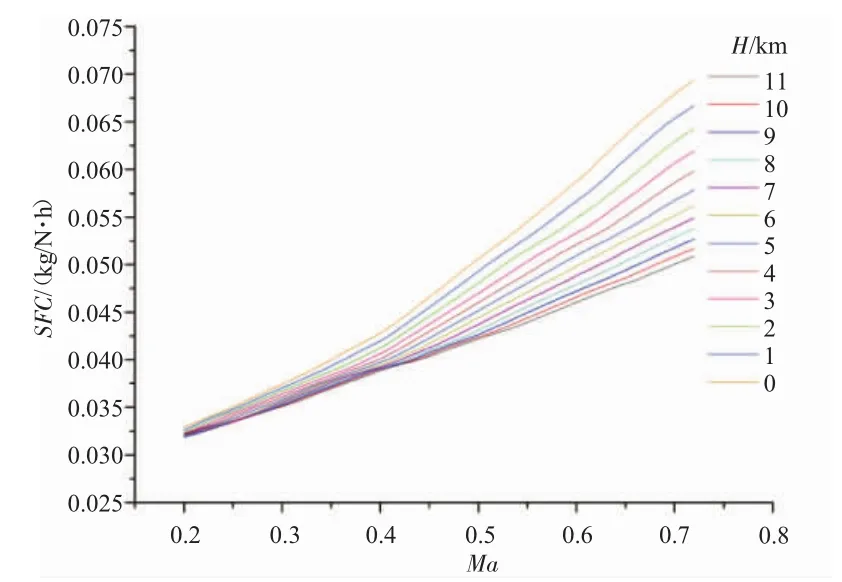
图8 固定转速调节下耗油率随高度速度的变化

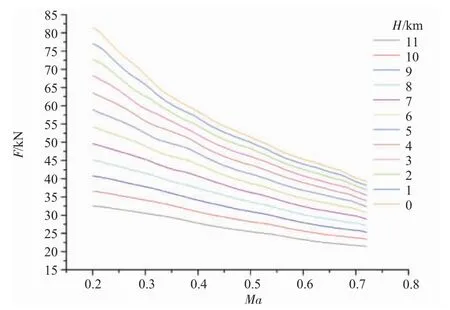
图9 固定叶尖速度调节下推力随高度速度的变化

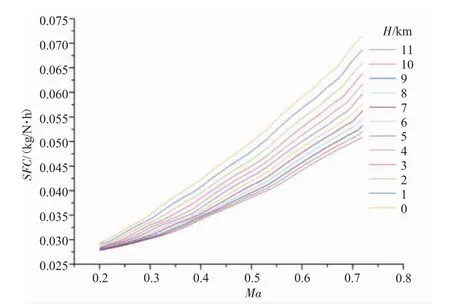
图10 固定叶尖速度调节下耗油率随高度速度的变化

固定叶尖速度调节下推力和耗油率随高度速度的变化如图9、10所示。推力和耗油率随高度、速度的变化规律与固定转速调节规律相近，但在马赫数较低时，采用固定叶尖速度的调节规律推力耗油率性能更优。在相同高度下，飞行速度降低时，叶尖速度不变，桨叶转速提高，因此推力较固定转速调节时更大；而提高桨叶转速需要减小桨扇安装角，桨扇推进效率提高，耗油率因此进一步降低。

5 结论

本文分别探讨了传统单排桨和对转双排桨的计算方法，以及行星差动齿轮结构的功率分配方法，并在此基础上建立了开式转子发动机整机全包线稳态性能计算模型。通过整机模型，深入研究了开式转子发动机的调节计划及其对应的高度速度特性，得到如下结论：

（1）对转桨气动计算模型及其组成的开式转子发动机整机模型可以满足一定的精度需求；

（2）固定桨扇叶尖速度的调节计划在较低飞行速度下具有高推力低油耗的优点，可以获得较好的全包线性能。

[1] Mikkelson D C,Mitchell G A,Bober L J.Summary of recent NASA propeller research[R].NASA TM-83733.

[2] Rosario R D,Wahls R,Madavan N.NASA subsonic fixed wing project overview[C]//NASA Fundamental Aeronautics Program 2012 Technical Conference.2012.

[3]Berton J J,Fisher K L,Haller W J,et al.Refined exploration of turbofan design options for an advanced single-aisle transport[M].Virginia：National Aeronautics and Space Administration,Langley Research Center,2011：1-3.

[4] Weisbrich A L,Godston J,Bradley E.Technology and benefits of aircraft counter rotation propellers[R].NASA-TM-82983.

[5] Weisbrich A L,Godston J,Bradley E S.Technology and benefits of high speed aircraft counter rotation propellers[R].NASA CR-168258.

[6] 刘沛清.空气螺旋桨理论及其应用[M].北京：北京航空航天大学出版社，2006：26－49.LIU Peiqing.Theory and application of air propeller[M].Beijing：Beijing University of Aeronautics and Astronautics Press,2006：26－49.(in Chinese)

[7] McLemore H C,Cannon M D.Aerodynamic Investigation of a four-blade propeller operating through an angle-of-attack range from 0 to 180 degrees[J].Technical Report Active&Image Library,1954（7）：1-14.

[8] 祁宏斌，周人治，黄红超，等.开式转子发动机对转桨扇性能建模研究[J].燃气涡轮试验与研究,2012（1）：20-24.QI Hongbing,ZHOU Renzhi,HUANG Hongchao,et al.Modeling of counter-rotating propfan performance of open rotor engine[J].Gas Turbine Experiment and Research,2012（1）：20-24.(in Chinese)

[9] Bellocq P,Sethi V,Cerasi L,et al.Advanced open rotor performance modelling for multidisciplinary optimization assessments[C]//ASME Turbo Expo 2010：Power for Land,Sea,and Air.American Society of Mechanical Engineers,2010：287-302.

[10] Hoff G E.Experimental performance and acoustic investigation of modern,counter rotating blade concepts[R].NASA-CR-185158.

[11] Reid C.Overview of flight testing of GE aircraft engines UDF engine[R].AIAA-1988-3082.

[12] Hendricks E S,Tong M T.Performance and weight estimates for an advanced open rotor engine[R].AIAA-2012-3911.

[13] Dominy J,Midgley R A.A transmission for the contra-rotating prop-fan powerplant[R].AIAA-1984-1196.

[14] Dooner D B,Seireg A A.The kinematic geometry of gearing：a concurrent engineering approach[M].State of New Jersey：John Wiley and Sons,Wiley series in design engineering,1995：388-410.

[15] Bala A,Sethi V,Lo Gatto E,et al.PROOSIS—a collaborative venture for gas turbine performance simulation using an object oriented programming schema[R].ISABE-2007-1357.

[16] Hendricks E S.Development of an open rotor cycle model in NPSS using a multi-design point approach[C]//ASME 2011 Turbo Expo：Turbine Technical Conference and Exposition.American Society of Mechanical Engineers,2011：441-450.

Research on Open Rotor Engine Caculating Model and Control Schedule

TU Qiu-ye1,NI Li-wei1,YANG Xiang-ming1,ZHENG Heng2,JIANG Ping2
（1.School of Power and Energy,Northwestern Polytechnical University,Xi'an 710072,China；2.AECC Commercial Aircraft Engine Co.,Ltd.,Shanghai 200241,China）

Counter-rotating coaxial propellers with variable pitch blades are mostly implemented in the current advanced open rotor engine.An aerodynamic computing method of counter rotating propellers was verified through calculating the counter-rotating propeller map using two single propeller maps.Basing on the aerodynamic and thermal model of a two-spool turbojet engine,an open rotor performance model was established by adding a power turbine,a differential planetary gearbox and a pair of counter rotating propellers.With this model,the control schedules were studied.The difference between constant propeller speed strategy and constant tip speed strategy,their influences to the altitude and velocity characteristics were compared respectively.The results were demonstrated to be accurate by using the data of PROOSIS model,and the performance of open rotor engine under various design parameters and different control schedules could be precisely studied.Results show that the constant tip speed strategy had advantage of high thrust with low fuel consumption at a lower flight speed,and better performance of the whole envelope would be obtained.

open rotor engine;counter rotating propeller;power turbine;differential planetary gearbox;control schedules;overall performance

V 135.12

A

10.13477/j.cnki.aeroengine.2016.06.006

2016-06-04

屠秋野(1971)，男，副教授，研究方向为航空发动机总体设计与性能仿真；E-mail：tuqiuye@nwpu.edu.cn。

屠秋野，倪力伟，杨祥明，等.开式转子发动机计算模型及调节研究[J].航空发动机，2016，42（6）：36-43.TU Qiuye,NI Liwei,YANG Xiangming,et al.Research on open rotor engine calculating model and control schedule[J].Aeroengine,2016,42（6）：36-43.

（编辑：赵明菁）