基于多重分形的我国股票波动特征研究

张广林+黄洁仪+陈胡松+陈仁莲

【摘要】本文对上证指数收盘指数的收益率进行统计性描述，发现其呈现“尖峰胖尾”现象;采用Hurst指数检验法，运用软件分析出上证指数存在多重分形波动特征。并采用多重分形区趋势法（MF-DFA法），做出上证指数收益率序列的多重分形谱f（α）与奇异指数α的关系图，得出我国股票存在多重分形现象，有着显著长记忆性，且效果图优于文[5]，进而说明时间的选取影响着分形效果。

【关键词】多重分形  统计性检验  多重分形谱  波动特征

自1990年上交所成立以来，证券市场呈现出现晚、发展快，是一个典型的新兴市场。期间经历了各种风雨，2015年6月更显现“A股巨震”、“千股跌停”，一次次反映出我国金融体系的不成熟。基于此，金融市场的研究备受关注，而Peters[1]于1994年提出的分形市场假说（FMH）给金融市场的探索开辟了另一条道路。文[2]对欧美等国的证券市场的研究结果表明大多数市场具有明显的分形特征：自相似性、显著的Hurst指数。文[3]对我国沪深两市实证发现，股票价格的波动按照不同的统计尺度体现出自相似性，并呈现出“尖峰厚尾”的稳定分布特征。文[4]给出贵金属市场的多重分形结构由长自相关性和“厚尾”概率决定。文[5]运用MF-DFA法，得出沪深300股指期货收益率序列的多重分形谱f（α）与奇异指数α的关系图，进而说明收益率序列的标度指数也将不同。

本文从统计性检验和多重分形谱两个方面对上证指数的波动特征进行分析并探究其影响因素，得出在选取样本数据不同的时间段下，其效果图优于文[5]，进而说明时间段的选取影响着分形效果。

一、数据描述

本文选用样本数据为同花顺行情系统中的2010年8月2日至2016年8月1日的上证指数收盘指数。

首先对所得原始数据进行数据分析与预处理，剔除异常数据，余1458个有效数据。选用对数收益率为本文研究对象，即

Rt（τ）=lnP（t+τ）-lnP（t）（1）

式中：Rt（τ）为时间标度τ下t时刻的收益率;τ=1、5、22（对应为日、周、月）;P（t）为t时刻价格。

二、统计性描述

样本中共1458个日数据，291个周数据，66个月数据，采用J-B检验对数收益率是否满足正态性假定进行统计性描述，结果如图1.1-3.

图1.1 上证指数日对数收益率分布的直方图

图1.2 上证指数周对数收益率分布的直方图

图1.3 上证指数月对数收益率分布的直方图

表1.1 上证指数日、周、月对数收益率J-B统计量结果

表1.1为上证指数日、周、月对数收益率J-B统计检验结果。若变量符合正态分布，则K=3。而日、周、月数据的K值显著大于3，且呈现逐渐减小的趋势;P值也趋于零，这说明三组数据离正态分布的假设距离甚远。

对表1.1的变量，由上图1知，月收益率最接近正态分布。然而，在图1.3中可以看出，在月收益率0.15附近取值的概率远大于正态分布下该点的概率。进而可知上证指数的日、周、月对数收益率均呈现明显的“尖峰厚尾”现象，不符合正态分布特征。

三、数据处理

（一）多重分形区趋势法（MF-DFA）

Peng[6]等人在1994年研究DNA机理时采用消除趋势波动分析法（DFA）去分析时间序列的长自相关性。但DFA法仅适合分析一维的单重分形时间序列。2002年，Kantelhardt，J.W[7]等将多重分形和DFA结合，提出多重分形趋势波动分析方法（MF-DFA），其可以刻画时间序列在不同时间标度下的多重分形特征，步骤如下：

考察时间序列{x（t）}（t=1，2，…，N）的q阶配分函数Xq（s）：

Xq（s）=<|x（t+τ）-x（t）|q>，t=1，2，…，N-τ（2）

当q=2时，即为趋势消除波动分析法（DFA）[6]。而MF-DFA的前三步与DFA相同，这里省略，详见文献[8]。

第四步：对所有时间序列子区间取平均，即得q阶波动函数：

Xq（s）=[    （3）

第五步：对同一q，描绘Xq（s）对s的双对数曲线：

若q不变，Xq（s）随s的增大而增大。多项式的阶数m的变化也影响着Xq（s），且有s≥m+1。

如果时间序列X（t）具有标度特性，则Xq（s）与s成幂律关系：

（4）

且Xq（s）与s的双对数曲线以线性关系存在，即：

（5）

式中：h（q）为广义赫斯特指数（Hurst）。当h（q）为q的函数时， 时间序列X（t）具有多重分形特性;当h（q）=0.5时，序列{X（t）}不相关。

（二）赫斯特（Hurst）指数检验

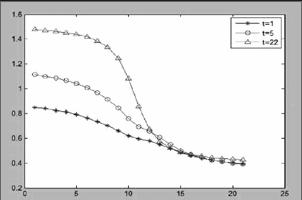
Hurst指数检验上述上证指数收益率序列，不妨取q∈[-10，10]的整数，运用MF-DFA法可得广义Hurst指数，如图3.1。

图3.1 上证指数q-Hurst图

由图3.1知，q的变化影响着Hurst指数h（q）。当τ=1、5、22时，h（q）总是随着q的增大而减小，因而可知上证指数在不同时间标度下存在多重分形特征。同时，观察到q=0的右边可能存在一个拐点，q=0的左边有h（q）>0.5，从而说明上证指数存在长期记忆性，而当h（q）<0.5，说明市场还存在反持续性。

（三）MF-DFA多重分形谱（MFS）分析

称α为局部分维或奇异指数，若定义α为序列中不同小区域内的生长概率，且令有相同α值的小区域构成一个子集。用f（α）表示有相同α值的子集的分形维或者奇异谱。奇异谱f（α）随α变化的曲线就是多重分形谱，其反映出α概率分布特征。因此，如果找到f（α）与α对应关系，那么可以描述出某一时间序列的多重分形谱。所以对式（5）进行勒让德变换：

α=h（q）+qh（q） （6）

f（α）=q[α-h（q）]+1 （7）

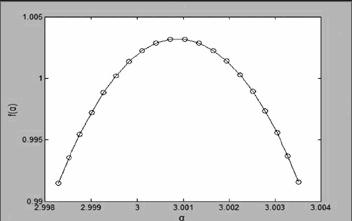
运用软件，对上证指数τ=1、5、22（日、周、月）的收益率作MF-DFA分析。其中，s为10～N/4天，q取[-10，10]中的整数，结果如图3.2。

由图3.2知：a）上证指数收益率序列多重分形谱接近于对称。τ=1时，α∈（2.9983，3.0035）。b）α随着时间标度的增加逐渐增大，f（α）的取值变化为（0.9915，1.0032），且当约q=0时取得最大值，进而得f（α）是一条光滑的曲线，故收益率序列的标度指数也将不同。

由图3.1和3.2知，上证指数q-Hurst图和收益率Rt（τ）的MF-DFA分析图比文[5]中的图显著，这说明时间段的选取影响着以上两个方面。进而再次验证时间序列中的多重分形行为存在两种成因：一是时间序列大小幅波动中不同的长范围相关性造成的;另一是波动中的“胖尾”概率分布引起的效应[9]。

图3.2τ=1时A股收益率Rt（τ）的MF-DFA分析

四、总结

综上，对上证指数的收益率进行统计性描述和Hurst指数分析，知其呈现“尖峰胖尾”现象，且存在多重分形波动特征。运用软件分析出上证指数存在多重分形特征，进而知其存在显著长记忆性，且其收益率序列的标度指数也不同。在选取样本数据不同时间段下，其效果图比文[5]显著，进而说明时间段的选取影响着分形效果。显著的长记忆性特征使得我国股票市场具有较大的风险性，具体表现在价格的连续同向波动，即波动呈现某种集群性，最终出现了“千股跌停”的现象。

参考文献

[1]Peters Edgar E.Fractal market analysis： applying chaos theory to investment and Economics[M].New York： John Wiley & Sons press，1994，216-237.

[2]Peters，E.Fractal market analysis：applying chaos theory to investment and economics[M].New York：John Wiley & Son Lnc.，1994.

[3]谭洁.分形理论在沪深股市研究中的应用[J].系统工程，2010， 4，15-23.

[4]孙梦野，王仲君.基于多重分形的贵金属市场风险研究[J].华中师范大学，2015，49（6）：831-837.

[5]陈仁莲.多重分形在沪深300股指期货市场的应用研究[J].市场研究，2016，6：43-45.

[6]Peng C-K，Buldyrev S V，et al.Mosaic organization of DNA nucleotides[J].Physical Review E，1994，（2）：1685-1689.

[7]Kantelhardt，J.W.Kantelhardt，S.A.Zschiegner，A.Bunde，S.Havlin，E.Koscielny-Bunde，and H.E.Stanley，Multifractal detrended fluctuation analysis of nonstationary time series[J].Physical A，2002（316）：87-114.

[8]徐化兵.基于分形市场假说的中国A股波动特征分析——以沪深300指数为例[D].南京航空航天大学硕士论文，2011.

[9]苑莹，庄新田.基于多重分形的金融市场复杂特特性分析及应用：以中国股票市场为研究对[M].北京：中国经济出版社，2012.

基金项目：广东石油化工学院大学生创新创业培育计划项目（2015pyA027）。

作者简介：陈仁莲，女，讲师，研究方向：分形几何，统计。