物理金融——金融中的纤维束

【摘要】纤维束是物理金融中的重要组成部分，纤维束由基底和这个基底上的点相联系的纤维构成，也就是纤维依附基形成纤维束，而基依附于基底存在。基底的不同导致基的分布受到限制，进而形成不同的纤维束。本文将纤维束进行分解，以基底的差异为区分度对纤维束进行了新的划分，在此基础上对应于金融的不同资产组合。

【关键词】纤维束  基底  纤维  资产组合

一、引言

美国次贷危机引发的金融危机席卷全球，由此引发全球金融危机、经济危机和欧债危机，至今其影响还存在。2008年之后，众多经济物理学家和经济学家反思传统经济学的弊端，呼吁对经济学理论进行根本的科学革命，并指出金融物理学的理论意义和实践价值[1]。

卡里尔·伊林斯基在《金融物理学——非均衡定价中的测量建模》一书中用一种非正式和直观的说法来介绍纤维束——纤维束就是由一个个相同的子空间组成的，这些子空间相互粘连在一起从而形成了整个空间。完全相同的子空间被称作是纤维，而将这些纤维连接在一起的子空间被称作是基底。这样就可以认为纤维束是纤维和基底的组合体[2]。

本文首先对纤维束进行一定的分解，将纤维束分为基底和纤维两部分，从基底的不同来介绍几种纤维束类型，并将简单介绍纤维束如何适用于金融这一不断变化的学科。

二、纤维束的划分

（一）以线为基底的纤维束

这种类型的纤维束的基底是直线或者曲线，作为基的点都在这条线上，而以基相联系的纤维则是互相平行的直线。

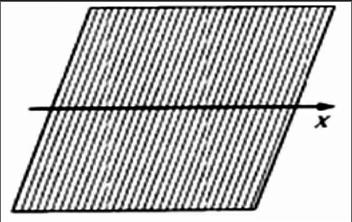
1.以直线为基底的纤维束。若纤维束的基底是一条直线，基是该直线上的点，纤维是与基底相交的无数条直线，那么我们可以勾画出这样的纤维束是二维的平面。选用最基础简单的二维平面为例，以X轴作为基底，X轴上的点为基，而过基且与基底垂直的直线作为纤维，这些纤维是相互平行的（见图1）。

图1 横轴是基底，与横轴正交的直线是纤维，而交点则是基

图1中的纤维束是最常见的平面纤维束，在这个图中，该纤维束的维度就等于基底（B）的维度加上纤维（F）的维度，即dimE=dimB+dimF。这样纤维束上任意一点的位置可以通过一对坐标来描述，像是（b，f），其中，f是该点所在纤维上的位置，b是纤维本身所在基底上的位置。

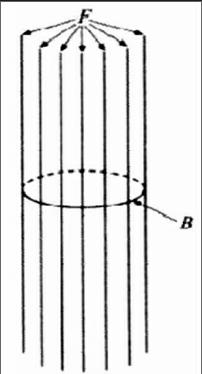
2.以圆环为基底的纤维束。如果将作为基底的直线弯曲成一个圆环，二维平面的纤维束将变成一个管状图形，这将得到一个不同类型的纤维束。新的纤维束具有圆形的基底（B）和直线纤维（F）（见图2）。

如果对以圆环为基底的纤维束上的位置用坐标（b，f）进行描述，我们会发现坐标出现了不同之处：在直线上的坐标可以从负无穷大到正无穷大，圆上的坐标却只能在0到2π之间进行变化，且坐标0与2π坐标是重合的。

（二）以面为底的纤维束

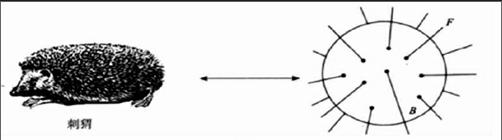
以面为底的纤维束的底面可以是平面也可以是曲面，可不管是平面还是曲面，纤维束上某点坐标已经不能简单用一个点来表示纤维本身所在基底上的位置。这里，选用标准的纤维束（见图3）——刺猬——来描述其特点。

图3

此纤维束的基底是曲面，纤维是与基底相切的发散直线，可知想要用坐标来描述纤维束上某点的位置，纤维上的位置是很好确定的，令我们为难的是纤维本身位置的确定。（B，F）代表纤维束上某点的坐标，F是一个简单的实数，B不再是简单的数，而是B=B（b），需要用向量来表示的某一位置。此时，纤维束的维度也将发生变化，而这变化是跟随基底的变化进行的。

考虑到纤维束的基底是如此变化的，那是不是也存在以面为底纤维如此变化的纤维束呢？是的，这样的纤维束（见图4）也是存在的。

图4

在这种纤维束中，基底和纤维都是变动的，不再是简单的数值。纤维束的基底是曲面，所以要确定纤维的位置B=B（b），需要用向量来确定，纤维上的位置也需要用向量来表示F=F（b）。这样的话，纤维束的维度跟随两个变量的变化而变化。

三、金融资产适用的纤维束

通过上面对纤维束的一些简单介绍，发现纤维束的基底和纤维可以分别当做是单独的坐标系，而且这两套坐标系可以具有不同的意义。想要细致描述一个金融资产组合的特征，是需要两套坐标系的，一套用来描述组合的货币价值，另一套描述组合中各种资产所占的比例[3]。于是，我们可以用纤维束来描述资产组合或者将资产组合空间看作是一个纤维束。纤维束的基底是资产组合的所有可能结构构成，组合的所以可能的货币价值是基底上的半线纤维（组合的货币价值不能为负，故选用半线纤维）。一般纤维束的纤维是没有交集的，他们之间是依赖基底进行变换的，也就是基底实现了纤维之间的连通。

首先通过一个外汇的例子来了解纤维束是如何作用于金融资产组合的。现在我们有五种货币，分别是英镑、美元、德国马克、法国法郎、日元，这五种货币我们是无法根据其纸张的数量来比较大小，只有将它们换算为同种货币才能进行比较。选用最一般的以面为底的纤维束，在基底上任意选五个点及该点上的纤维作为某种货币，纤维的长度代表该种货币的数量，这种纤维束（见图5）就是资金空间。

图5 资金空间纤维束

图5中，标着GBP、USD、DM、FF、JY的五个点便是基底上选的基，基上的纤维是半线纤维，而纤维之间的连通是依赖于基底进行的。也就是想要进行两种或多种货币之间的换算或者比较，就需要将货币换算成同一种货币，而换算的过程就是在基底进行的，基底实现了不同货币之间的跳跃。

接下来看一个净现值计算的纤维束空间的例子。

首先简单介绍一下什么是净现值法（NPV）。令NPV站住脚跟的原理是：资金有时间价值。时间价值可以通过贴现过程来展示。对不同货币标明面值的资金进行比较首先需要将它们兑换成同样的货币，同理，货币相同时间不同的资金也不能直接进行比较，需要将它们转换到统一的时点上，而这一过程反映的就是资金的时间价值。

NPV公式：

P是当前的一笔资金，F是T年后收到的资金数量，r是投资过程的利率

NPV过程中使用的利率被称作是贴现率

贴现因子：

假设我们现在有100英镑和一年后有103英镑可选择，这时候应该怎样选择呢，肯定是选择两者相比更大的那个，但是这两种选择并不在同一时间上，我们无法比较出跨越时间的两种选择，也就是需要把这两种选择换算到同一时间上。这里就需要NPV公式，可以将当前的100英镑按一定的年利率换算到一年后的货币数量，或者将一年后的103英镑换算为当前一定的货币数量。同种货币关于时间的变化也存在纤维束空间（见图6）。

图6 净现值纤维束空间

在净现值纤维束空间里，基底实现了时间的跨越，也就是基底是资产组合的时间轴，纤维则是不同时间的货币数量，贴现过程实现了代表着不同数量货币的纤维之间的连通。

四、结束语

当投资者在进行货币交换和净现值计算时，可以认为是在纤维束中进行移动的。任何交易市场都存在一个可移动的纤维束空间，且这并不依赖于交易资产的特征、市场参与者的偏好以及市场的某些性质。将纤维束空间与资产组合结合到一起有助于我们一定程度上客观直接的研究金融市场的波动和趋势。

参考文献

[1]周炜星.《经济物理学》简评.新书介绍，2014.

[2]刘建国.现代金融学研究的新视角——《金融物理学导论》评介.华东理工大学学报，2007.

[3]施其敏，包菡.浅析货币时间价值的应用.《心事》，2014.

作者简介：李玉娟（1991-），女，汉族，山东潍坊人，山东科技大学数学系统与科学学院研究生，研究方向：金融数学与金融工程。