滚珠直线导轨副分形磨损模型及精度退化研究①
王 民 蒋雄飞 张 巍 周 霜
(*北京工业大学机械工程与应用电子技术学院先进制造技术北京市重点实验室 北京 100124)(**电火花加工技术北京市重点实验室 北京 100191)
滚珠直线导轨副分形磨损模型及精度退化研究①
王 民②***蒋雄飞*张 巍*周 霜*
(*北京工业大学机械工程与应用电子技术学院先进制造技术北京市重点实验室 北京 100124)(**电火花加工技术北京市重点实验室 北京 100191)
为研究滚珠直线导轨副磨损和精度损失规律,基于赫兹接触理论建立了滚珠直线导轨副力学模型。使用分形函数表征滚珠和滑块滚道接触区表面,并采用结构函数法求得滚道表面的分形参数。考虑滚珠和滑块滚道之间的润滑状态,在分形接触模型下对滚珠和滑块滚道接触区域的微分形表面进行了受力分析。基于粘着磨损理论分析了滚珠和滚道接触面微凸体的磨损过程,并在此基础上结合蠕滑理论建立了滚珠和滚道接触面的分形磨损模型。最后,以某型号滚珠直线导轨副为研究对象进行了仿真分析,得到不同载荷和不同跑合距离下滚珠直线导轨副磨损和精度退化规律。
滚珠直线导轨副, 分形理论, 精度退化, 蠕滑理论
0 引 言
滚珠直线导轨副是滚动直线导轨副的一种,其具有定位精度高、动摩擦系数小、可维护性好等优点。滚动直线导轨副作为机床的关键功能部件得到了越来越广泛的应用,它对提高机床的加工精度起着非常重要的作用。但其基础理论目前尚不很完善[1],尤其对其精度失效规律及其精度保持性缺乏准确的理论分析方法。
滚珠直线导轨副的精度保持性主要取决于导轨副运行过程中因摩擦磨损导致的导向精度和导轨副接触刚度的退化。目前对于滚珠直线导轨副的研究还主要集中在滚珠直线导轨副的刚度研究上,磨损方面的研究相对较少。钟洋[2]基于Hertz接触理论和刚体动力学建立了导轨副的刚度计算模型,并结合Archard磨损理论建立了导轨副的磨损预测模型,但Archard磨损公式主要是适用于滑动摩擦磨损,且未考虑不同摩擦接触面的几何差异性的影响。自从Mandelbrot提出分形几何理论以来,分形几何理论被广泛应用在各不同学科领域。由于分形理论在描述机械加工表面时具有与尺度无关的特性,分形理论被引入到接触力学和摩擦学中[3]。Zhou等人基于M-B分形模型建立了磨合磨损预测模型[4]。房桂芳[5]在机械密封端面接触分形模型基础上,依据Archard粘着磨损理论,建立了机械密封端面粘着磨损分形模型。分形理论可以有效地表征机械加工表面的形貌,基于分形理论建立的摩擦学研究模型比基于传统的模型更具合理性和有效性[6]。
滚珠直线导轨副中滚珠滚道接触磨损为滚动摩擦磨损,磨损主要发生在硬度相对较低的滑块滚道上。导轨副运行过程中在外载荷的作用下,滚珠与滚道接触区域内滚珠将会产生微量的弹性变形,形成弹性相对滑动,并由粘着效应形成粘着节点剪断或脱落,从而形成磨屑。为了计算滚珠滚道相对滑动距离,本文引入滚动接触蠕滑理论计算滚珠和滚道间的相对滑动距离[2]。本文基于分形理论和赫兹接触理论,考虑滚珠和滚道间润滑状态,并结合粘着磨损理论和蠕滑理论,研究了滚动直线导轨副磨损和精度退化规律。
1 滚珠直线导轨副力学模型
图1为滚珠直线导轨副受外载荷时的截面图,导轨副有4列滚珠,每列滚珠的承载滚珠数为ns,每列滚珠的接触角均为α,每列滚珠所受接触面的法向载荷为Qi(i=1,2,3,4),在4列滚珠的对称中心点建立如图1所示坐标系。对其进行力学分析可知:
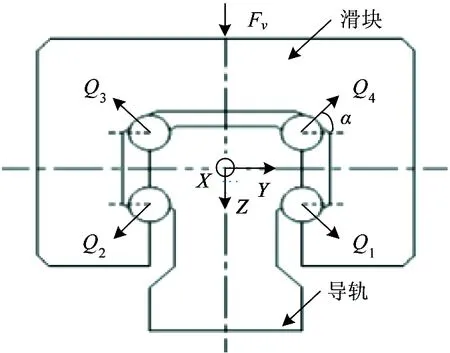
图1 滚珠直线导轨副受力图
Q1=Q2, Q3=Q4
(1)
(Q1+Q2-Q3-Q4)nssinα+Fv=0
(2)
滚珠与滑块滚道之间的接触满足空间Hertz点接触理论,其接触区域为椭圆形区域。钢制滚珠直线导轨副接触变形计算公式为[2]
(3)
(4)
(5)
式中,Q为滚珠所受载荷,δ为滚珠变形量,Σρ为滚珠和滚道的综合曲率,a′和b′分别为椭圆形接触区域的长半轴和短半轴长度。ma、mb和2K/πma是和椭圆主曲率函数相关的系数,椭圆的主曲率之和与主曲率函数的计算式如下:
(6)
(7)
式中,Da为滚珠直径,f为滑块滚道曲率半径与滚珠直径比(曲率比)。依据主曲率函数和主曲率之和的值,查表可以得到ma、mb和2K/πma。
为了提高滚珠直线导轨副承载刚度,制造厂家一般通过给每列滚珠施加预紧力以达到提高刚度的目的。因预紧力的作用滚珠会产生初始变形δ0,Q0和δ0之间的关系为
(8)
在受外载荷Fv的作用下,每列滚珠的变形为δi(i=1,2,3,4),滑块会在Z轴的方向产生一个位移量δv,根据滚珠直线导轨副的变形几何协调关系可以得到:
(9)
(10)
δ1=δ2, δ3=δ4
(11)
当滚珠的变形量δi≤0时,滚珠因预紧力而产生的变形消失,滚珠脱离接触,滚珠受力Qi=0。
2 分形接触模型
2.1 滚道表面形貌分形表征
机械加工表面不仅具有统计特性,而且具有分形特性,为了便于分析,将滚珠和滑块滚道椭圆接触区域离散为一系列8μm×8μm微分形表面,微分形表面可以用W-M函数来表征[7]:
(12)
式中z(x)为粗糙表面的随机轮廓高度,x为轮廓的坐标位置,G是分形表面的特征尺度系数,D′是表面轮廓分形维数,γn决定了粗糙表面的频率谱,一般取γ=1.5。nl依赖于采样长度L,且γnl=1/L。
分形参数可通过功率谱函数法和结构函数法求取,但功率谱函数法得出的结果误差较大,结构函数法要优于功率谱法[8]。结构函数法是通过求得轮廓曲线的结构函数,并在结构函数的双对数坐标轴上做回归分析来获取轮廓的分形参数。轮廓曲线的结构函数定义为
E(τ)=
(13)
式中τ是x方向的任意增量,<·>表示空间平均值。
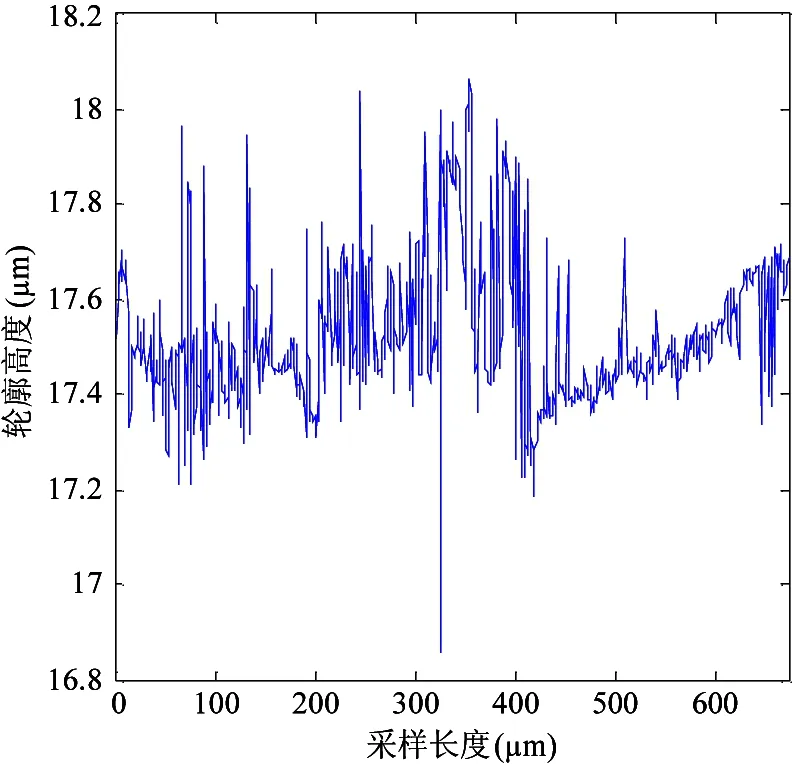
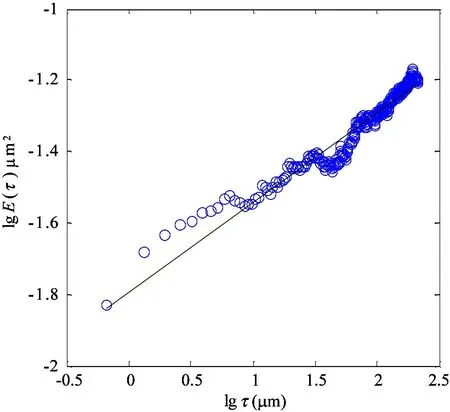
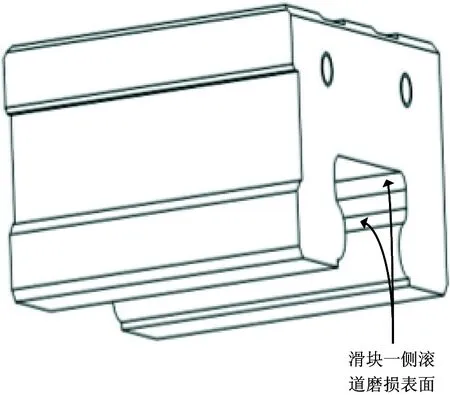
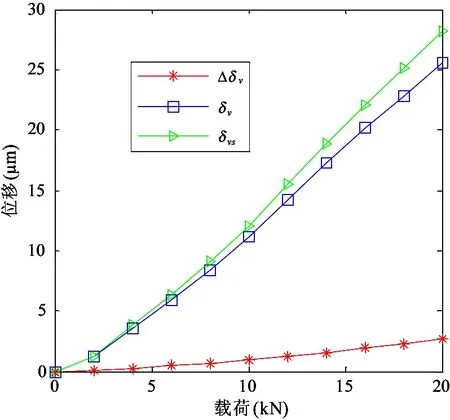
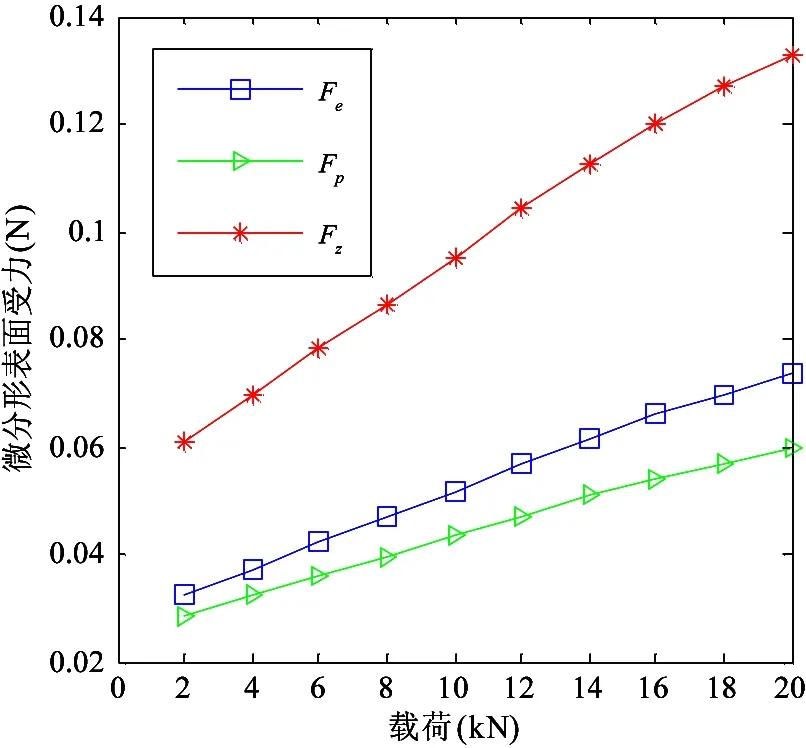
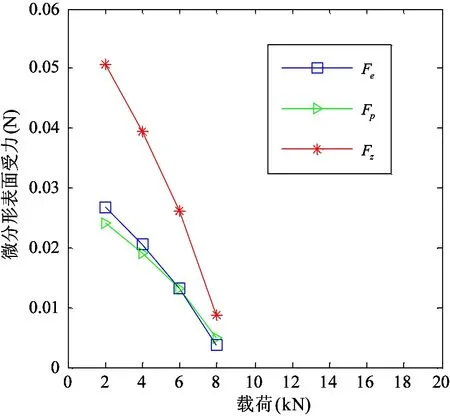
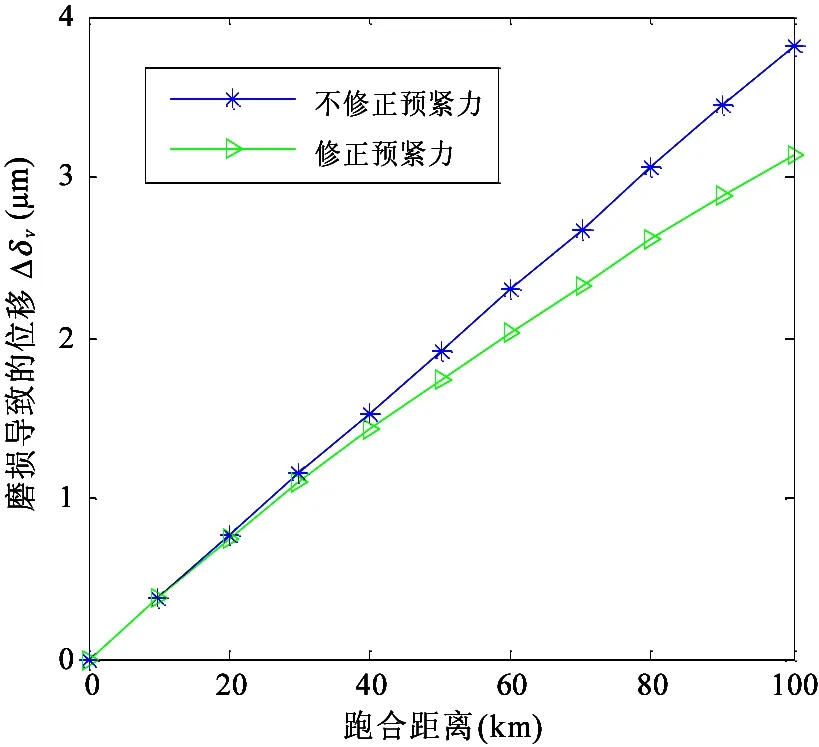
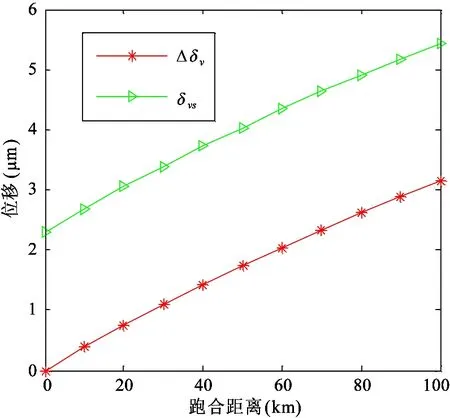
将结构函数表示在双对数坐标轴上,lgE(τ)和lgτ成直线关系,且直线斜率ks满足0 ks=4-2D′ (14) B=lgCG2(D′-1) (15) (16) 式中B为直线的截距,函数Γ为第二类欧拉积分,即Gamma函数。 运用显微系统测量某型号为LG20的滚珠直线导轨副滑块滚道表面轮廓,测量区域为500μm×675μm,采样点数为768×1024,根据测量数据绘制滚道三维轮廓图,如图2所示。 图2 滑块滚道三维轮廓图 在675μm方向任取一组1024个数据点,采用结构函数法由式(13)~(16)可求得分形参数D′和G,二维表面轮廓图和结构函数双对数图分别如图3和图4所示。 利用MATLAB软件中多项式拟合函数拟合结构函数双对数图,算得D′=1.874,G=2.38×10-8m,因此滑块滚道表面具有分形特性,满足分形理论的使用条件。 图3 滑块滚道表面轮廓高度曲线 图4 结构函数双对数图 2.2 分形接触力学分析 由于滚珠尺寸远大于椭圆区域尺寸,因此将滚珠与滑块滚道之间的接触简化为光滑滚珠刚性平面与粗糙的具有分形特性的滑块滚道面间的接触。刚性平面相对于粗糙表面挤压形成的微凸体截断尺寸服从岛屿分布,三维表面微凸体截断尺寸分布为[10] (17) 式中D为表面分形维数,与式(12)中D′之间的关系为D=D′+1,a为接触面上微凸体截断接触面积,aL为微凸体最大截断接触面积。 根据微分形表面弹塑性力学分析可得[10] (18) (19) (20) (21) 式中,ac为微凸体临界截断接触面积,当a≤ac时,微凸体变形为塑性变形;当a>ac时,微凸体变形为弹性变形。E*为综合弹性模量,H为滑块滚道材料硬度,与材料的屈服强度σs相关,一般取H=2.8σs。Fe为微分形表面弹性负载总和,Fp为微分形表面塑性负载总和,S为微分形表面微凸体与刚性平面的总接触面积。 微分形表面微凸体所受的总载荷Fz为弹性负载和塑性负载之和: Fz=Fe+Fp (22) 实际工况下,滚珠与滚道之间添加润滑油或者润滑脂润滑。假定滚珠和滚道之间的润滑为边界润滑状态,实验证明[11]微凸体之间产生的流体动压力约等于摩擦副中较软材料的屈服强度σs。假定所有的微分形表面均匀的承担椭圆接触面的压力,对微分形表面受力分析可得 σs(Aα-S)+Fz=PAα (23) (24) 式中微分形面名义面积Aα=64μm2,P为椭圆接触区域平均接触应力。综合式(18)-(24)可得 (25) 其中: (26-a) (26-b) (26-c) (26-d) 由式(25)、(26)可以求出微分形面中微凸体的最大截断接触面积aL。 假定粗糙表面的形貌具有各向同性的特征,将粗糙表面上的微凸体近似为轴对称体,接触面底圆半径为l/2,则单个微凸体的截断接触面积a和底圆半径l/2的关系为 a=π(l/2)2 (27) 由W-M分形函数可知,微凸体在底圆以上的轮廓线可以近似为余弦波,其函数表达式为[12] (28) 单个微凸体的体积V(a)可计算得到[5] (29) 当单个滚珠和滚道接触面相对滑动距离为l时,因滚珠滚道间相对滑动所产的生磨屑总体积为 (30) 产生ΔV的磨损体积时摩擦副的平均滑动距离la为[13] (31) 根据蠕滑理论,滚珠在滑块滚道上的相对滑动距离ls可由下式计算[2]: ls=μSz (32) (33) 式中μ为蠕滑率,Sz为滑块的跑合距离,δi为滚珠的弹性变形量,Da为滚珠的直径。 由于在磨损的过程中,并非所有的粘着点都会产生磨屑,因此引入分形磨损系数Kf,对磨损体积进行修正。当滑块运动Sz后,第i列滚珠引起的对应滑块滚道的磨损体积Vz,i为 (34) 每列滚珠产生的总磨损量随着滚珠的运动均匀分布在滑块滚道长度lr上,第i列滚珠引起的对应滑块滚道接触面法向磨损深度hi为 (35) lr=nsDa (36) 综合式(34)-(36)可得 (37) 导轨副在受图1所示载荷下运动,滑块滚道磨损会使滑块产生Z向位移Δδv,根据导轨副的结构特征可得 Δδv=(h3-h1)sinα (38) 综合考虑滚珠与滚道弹性变形和磨损对导轨副的运动精度的影响,可得滑块在Z轴方向的总位移量δvs用下式表示: δvs=δv+Δδv (39) 滚珠直线导轨副发生磨损后,滚珠预紧力会退化,初始变形量变小,在磨损量计算中需要随跑合距离的增加不断对初始变形量进行修正以保证计算准确性。每列滚珠初始预紧变形随磨损过程导致的变化量Δδ0,i(i=1,2,3,4)可根据导轨副的结构特征得到: (40) 为了验证所建磨损模型的合理性,以型号为LG20的滚珠直线导轨副(图5所示)为对象进行磨损仿真分析,导轨副的主要参数如表1所示。 图5 LG20滚珠直线导轨副 初始变形δ0(mm)0.004滚珠直径Da(mm)3.969曲率比f0.51承载滚珠数ns(个)12接触角α(°)45 滑块和滚珠的材质均为高碳铬轴承钢GCr15,E*=1.143×105MPa,σs=518.4MPa。宿月文[14]等人的研究表明磨损系数随着载荷的增大而减少并趋于稳定值,本文取Kf=5×10-4对滚珠直线导轨副磨损及精度损失进行退化规律仿真计算。磨损主要发生在滚动直线导轨副滑块的滚道上,滑块为对称结构有4个磨损表面,滑块一侧滚道磨损表面如图6所示。 图6 滑块滚道磨损表面 图7是在滚珠直线导轨副在外加载荷下工作初始阶段,即跑合距离为5km时的仿真结果。从图7可见,载荷越大,滑块总变形、弹性变形以及磨损产生的位移均越大,弹性变形δv的仿真曲线与滚珠直线导轨副刚度曲线一致。从图中可以看出受外载荷较大时,滑块弹性变形量δv远大于磨损产生的位移,滑块总位移曲线变化趋势与弹性变形曲线变化趋势一致。 图7 Sz=5km下滑块位移量 图8和图9分别是滚珠直线导轨副在外加载荷下工作初始阶段,即跑合距离为5km时,滑块第3、4列滚珠和第1、2列滚珠和滑块滚道接触区域的滚道微分形表面受力图。从图8可见,载荷越大,第3、4列滚珠和滑块滚道接触区域的滚道微分形面的弹性载荷、塑性载荷以及弹塑性载荷总和均越大。从图9可见,载荷越大,第1和第2列滚珠和滚道接触区域的滚道微分形面的弹性载荷、塑性载荷以及弹塑性载荷总和均越小,且随着外载荷的增加,滑块第1列和第2列滚珠与滚道表面脱离接触。 图8 Sz=5km下滑块第3、4列滑块滚道微分形表面受力 图9 Sz=5km下滑块第1、2列滑块滚道微分形表面受力 图10为滚珠直线导轨副在恒定载荷Fv=2kN下,不修正滚珠预紧力和修正预紧力时,由磨损导致的位移Δδv随跑合距离增加的变化关系图。从图10中可以看出预紧力对导轨副的磨损有很大的影响,图中修正预紧力的曲线为每运行10km修正一次预紧初始变形量δ0。修正预紧力后磨损导致的位移比不修正预紧力的要小。在实际磨损过程中,发生磨损后滚珠的预紧力变小,滚珠的总变形会减少,磨损趋势会变缓。 图10 Fv=2kN时磨损导致的滑块位移 图11为考虑预紧力退化后,因磨损产生的位移Δδv和滑块总位移δvs随滑块跑合距离的变化曲线。在恒定外加负载下导轨弹性变形δv近似为定值,故导轨副在外加负载作用下Z向总位移量随着磨损导致的位移量变化趋势一致,且随着跑合距离的增加,磨损导致的位移量所占比重不断加大,导致滚珠直线导轨副导向精度降低。当磨损导致的位移量在滚道法向方向的位移分量超过滚珠的预紧初始变形量时,滑块下两列滚珠与滚道脱离接触导致刚度丧失。 图11 Fv=2kN时滑块的总位移及磨损导致的位移 本文从赫兹接触理论出发分析了滚珠直线导轨副的受力与变形,建立了导轨副力学模型。引入分形理论来表征滑块滚道表面,并结合蠕滑理论以及粘着磨损理论建立了滚珠直线导轨副在润滑状态下的分形磨损模型。首次将分形理论引入到滚动直线导轨副的磨损研究中,相比于用Archard磨损理论建立的导轨精度损失模型,本文所建分形磨损模型综合考虑了接触表面的分形参数、润滑条件、材料的表面特性等因素,更加符合实际情况。同时本文所建精度损失模型充分考虑了磨损过程中预紧力退化对导轨副精度退化的影响,对预紧力进行了修正,得到了更加准确的精度损失模型。本文所建立的精度损失模型可为研究滚珠直线导轨副精度退化规律和开展精度保持性试验研究提供理论依据。 [1] 刘曙光. 滚柱直线导轨副的力学性能分析:[硕士学位论文]. 武汉:华中科技大学机械科学与工程学院, 2011. 1-12 [2] 钟洋. 滚动直线导轨副精度损失保持性基础理论研究与实验台设计:[硕士学位论文]. 南京理工大学机械工程学院, 2014.9-20 [3] 葛世荣,朱华. 摩擦学的分形. 北京:机械工业出版社, 2005. 112-124 [4] Zhou G Y, Leu M C, Blackmore D. Fractal geometry modelfor wear prediction.Wear,1993,170(1):1-14 [5] 房桂芳,滕文锐,刘其和等. 机械密封端面黏着磨损分形模型. 流体机械, 2013, 41(1):35-41 [6] 陈国安,葛世荣,王军祥. 分形理论在摩擦学中应用. 摩擦学学报, 1998,18(2):179-184 [7] Majumdar A, Tien C L. Fractal characterization and simulation of rough surfaces:Wear, 1990, 136(2): 313-327 [8] 张波. 硬盘表面微观形貌的分形表征及模拟:[硕士学位论文]. 长春:吉林大学机械科学与工程学院, 2004.20-48 [9] 董霖. 基于分形理论的弹塑性接触及磨合磨损预测模型的研究:[硕士学位论文]. 成都:四川大学制造科学与工程学院, 2000. 9-14 [10] Yan W, Komvopoulos K. Contactanalysis of elastic-plastic fractal surfaces.JournalofAppliedPhysics, 1998,84(7):3617-3624 [11] 李传乾. 机床摩擦磨损与润滑. 北京:机械工业出版社, 1990. 97-100 [12] Majumdar A, Bhushan B. Fractal model of elastic-plastic contact between rough surfaces.JournalofTribology, 1991,113(1):1-11 [13] 王新华,张嗣伟,樊启蕴. 基于分形几何理论的粘着磨损模型. 石油大学学报, 1999,23(6):50-53 [14] 宿月文,陈渭,朱爱斌等. 分形特征表面接触磨损模拟. 西安交通大学学报, 2013,47(7):52-56 Studies of linear ball guideways’ fractal wearmodel and accuracy degradation Wang Min***, Jiang Xiongfei*, Zhang Wei*, Zhou Shuang* (*Advanced Manufacturing Technology of the Key Laboratory of Beijing Municipality College of Mechanical Engineering and Applied Electronics Technology, Beijing University of Technology, Beijing 100124)(**Beijing Municipal Key Laboratory of EDM Technology, Beijing 100191) Based on the Hertz contact theory, a mechanical model of linear ball guideways was built to study the wear rule and accuracy degradation of linear ball guideways. The contact area between the ball and the slider’s raceway was characterized by the fractal function, and the raceway’s fractal parameters were obtained by using the structure function analysis method. Under the considering of the lubrication state between the ball and the slider’s raceway, the asperities load capacity was obtained by using the fractal contact model. The wear between the ball and slider’s raceway was analyzed through the adhesive wear theory, and then, the fractal wear model of linear ball guideways was established with the creep theory. Finally, the simulation analysis for a certain type of the linearball guideway was conducted, and the wear rules and accuracy degradation of the linearball guideway under different loads and running distance were obtained by the calculation simulation. linear ball guideway, fractal theory, accuracy degradation, creep theory 10.3772/j.issn.1002-0470.2016.03.007 ①国家科技重大专项(2012ZX04010021-001-004),国家自然科学基金(51575014),北京自然科学基金暨北京教委科技计划重点项目(KZ201410005010)和北京市自然科学基金委员会-北京市科学技术研究院联合(L150006)资助项目。 2016-01-21) ②男,1972年生,博士,博士生导师,教授;研究方向:机床动力学,振动测试与控制,切削过程监控,数控机床精度保持性等;联系人,E-mail: wangm@bjut.edu.cn(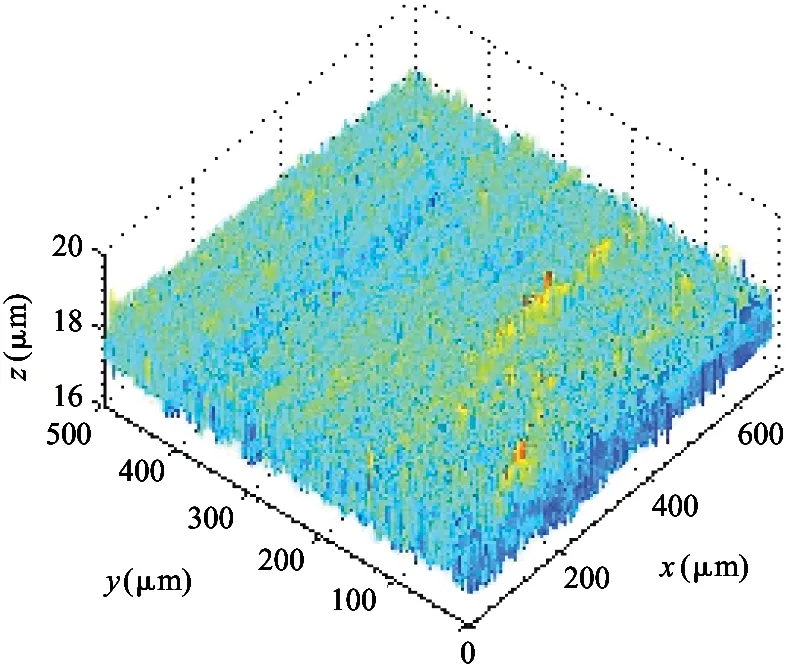
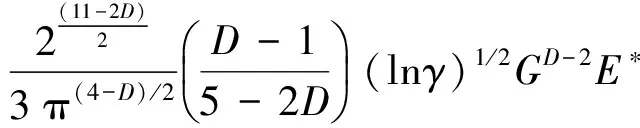
3 分形磨损模型
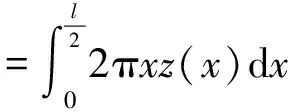
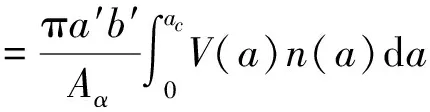
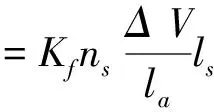
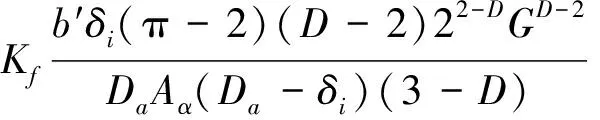
4 仿真计算与分析


5 结 论

