强震复发概率模型中的参数不确定性研究

郭 星 潘 华

1) 中国北京100082环境保护部核与辐射安全中心2) 中国北京100081中国地震局地球物理研究所



强震复发概率模型中的参数不确定性研究

郭 星1)潘 华2),

1) 中国北京100082环境保护部核与辐射安全中心2) 中国北京100081中国地震局地球物理研究所

在强震发生概率计算过程中， 往往只考虑参数的随机不确定性， 却很少考虑参数的认知不确定性． 本文以布朗过程时间(BPT)模型为例， 利用贝叶斯估计法定量分析了强震平均复发间隔的认知不确定性； 研究了在强震发生概率计算过程中如何考虑这种认知不确定性． 结果表明： 采用不同的强震复发间隔参数估计方法， 所得的参数认知不确定性存在明显差异； 在计算强震发生概率时， 是否考虑参数认知不确定性所得的结果存在较大差异．

强震发生概率 参数不确定性 随机不确定性 认知不确定性

引言

在计算强震发生概率时， 为考虑强震发生的时间记忆性， Utsu(1972)， Rikitake(1974)和Hagiwara(1974)基于弹性回跳理论(Reid, 1910)提出了一种更新概率模型， 该模型假定地震的发生符合更新过程． 此后， 国内外研究人员先后提出了诸多符合更新过程的概率分布模型， 其中比较常用的有对数正态模型(Nishenko， Buland， 1987)和布朗过程时间(Brownian passage time， 简写为BPT)模型(Ellsworthetal， 1999； Matthewsetal， 2002)．

对于任意一种概率分布模型， 若已知强震发生的概率密度函数f(T)和之前一次强震的离逝时间Te， 则可计算出断层源上未来一段时间ΔT内强震发生的条件概率(Wesnousky， 1986)， 即

(1)

1 强震复发概率模型中的参数不确定性研究

BPT模型是Ellsworth等(1999)和Matthews等(2002)在弹性回跳理论(Reid， 1910)基础上提出的强震复发概率模型． 该模型假定构造应力(或地震矩)在稳定加载过程中会受到一些自然随机事件的影响， 其概率密度函数为

(2)

1) 历史地震或古地震估计法． 若断层源上有2个以上的历史地震记载或古地震记录， 可以利用其时间间隔来估计强震的平均复发间隔．

(3)

(4)

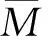
(5)

(6)

图1 平均复发间隔的认知不确定性概率密度函数图

(7)

复发间隔为T22的概率密度为

(8)

(9)

对于无强震复发间隔数据情况下的平均复发间隔的确定， 只能利用强震的特征地震震级进行估计． 根据特征地震的概念(Aki， 1984； Schwartz， Coppersmith， 1984)， 某些断层源在长期活动过程中， 重复发生的大地震往往表现出相似的破裂尺度和震级大小， 即特征地震震级的大小存在一定的随机不确定性． 若要利用地震矩释放率法来估算大地震的平均复发间隔， 则必须首先确定其特征地震震级的均值．

(10)

式中，σM为震级总的不确定性分布的标准差，σE和σA分别为特征地震平均震级的认知不确定性分布标准差和特征地震震级的随机不确定性分布标准差． 由式(10)可知， 只要σM，σE和σA这3个参数中确定了任意两个参数， 即可计算得到另外一个参数．

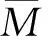
(11)

震级为M的地震所释放的地震矩M0可以由郭星(2014)给出的我国面波震级与地震矩的经验关系式计算得到, 即

lgM0=1.5M+8.61,

(12)

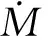
(13)

将式(12)带入式(13)并整理得：

(14)

将常用对数换为自然对数， 则上式变为

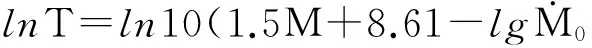
(15)

(16)

(17)

(18)

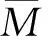
对于特征地震震级随机不确定性分布的标准差σA的确定， 根据BPT模型的概率密度函数及其变异系数α=0.34， 本文提出利用蒙特卡罗法随机生成10万个复发间隔数据， 再利用地震矩释放率即可得到10万个合成的震级数据， 对这些震级数据进行统计即可得到随机不确定性分布标准差σA， 再根据式(10)计算得到震级认知不确定性分布标准差σE．

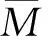
2 考虑参数认知不确定性的强震发生概率计算

(19)

(20)

2.1 已知一个强震复发间隔数据的强震发生概率计算

图2 考虑参数不确定性和不考虑参数认知不确定性情况下的BPT模型在未来10年强震发生概率计算结果的对比

2.2 已知两个强震复发间隔数据的强震发生概率计算

2.3 无强震复发间隔数据的强震发生概率计算

3 讨论与结论

本研究仅对强震复发概率模型中的参数不确定性的定量研究方法进行了探讨， 并未涉及强震复发概率模型本身的认知不确定性． 各种强震复发概率模型均基于一定的假设， BPT模型仅是其中一种较常用的强震复发概率模型. 在强震发生概率计算过程中还可以选用其它概率模型， 而采用不同的概率模型所得到的计算结果也是不同的， 这种因模型选择而带来的认知不确定一般可以采用逻辑树的方式进行处理．

郭星. 2014. 强震复发的随机特征滑动模型及其应用方法研究[D]. 北京: 中国地震局地球物理研究所： 39--43.

Guo X. 2014.StochasticCharacteristic-SlipModelandItsApplicationMethod[D]. Beijing: Institute of Geophysics， China Earthquake Administration： 39--43 (in Chinese).

郭星， 潘华. 2015. 强震复发间隔变异系数的一种计算方法[J]. 地震学报， 37(3): 411--419.

Guo X， Pan H. 2015. A method for computing the aperiodicity parameter of the strong earthquake recurrence interval[J].ActaSeismologicaSinica， 37(3): 411--419 (in Chinese).

Aki K. 1984.Asperities， barriers， characteristic earthquakes and strong motion prediction[J].JGeophysRes， 89(B7): 5867--5872.

Ellsworth W L， Matthews M V， Nadeau R M， Nishenko S P， Reasenberg P A， Simpson R W. 1999.APhysicallyBasedEarthquakeRecurrenceModelforEstimationofLong-TermEarthquakeProbabilities[R]. Reston， VA: U S Geological Survey Open-File Report： 99--522.

Hagiwara Y. 1974. Probability of earthquake occurrence as obtained from a Weibull distribution analysis of crustal strain[J].Tectonophysics， 23(3): 313--318.

Matthews M V， Ellsworth W L， Reasenberg P A. 2002.A Brownian model for recurrent earthquakes[J].BullSeismolSocAm， 92(6): 2233--2250.

Nishenko S P， Buland R A. 1987. A generic recurrence interval distribution for earthquake forecasting[J].BullSeismolSocAm， 77(4): 1382--1399.

Reid H F. 1910.TheMechanicsoftheEarthquake，theCaliforniaEarthquakeofApril18， 1906[R]. Washington: State Earthquake Investigation Commission， Carnegie Institution of Washington: 43--47.

Rikitake T. 1974. Probability of earthquake occurrence as estimated from crustal strain[J].Tectonophysics， 23(3): 299--312.

Schwartz D P， Coppersmith K J. 1984. Fault behavior and characteristic earthquakes: Examples from the Wasatch and San Andreas Fault Zones[J].JGeophysRes， 89(B7): 5681--5698.

Shimazaki K， Nakata T. 1980. Time-predictable recurrence model for large earthquakes[J].GeophysResLett， 7(4): 279--282.

Utsu T. 1972.LargeEarthquakesNearHokkaidoandtheExpectancyoftheOccurrenceofaLargeEarthquakeOffNemuro[R]. Hokkaido: Coordinating Committee for Earthquake Prediction: 7--13.

Wesnousky S G. 1986. Earthquake， quaternary faults， and seismic hazard in California[J].JGeophysRes， 91(B12): 12587--12631.

Parameter uncertainty analysis on probability model of strong earthquake recurrence

Guo Xing1)Pan Hua2),

1)NuclearandRadiationSafetyCenter，MinistryofEnvironmentProtection，Beijing100082，China2)InstituteofGeophysics，ChinaEarthquakeAdministration，Beijing100081，China

In the process of calculating probability for large earthquake occurrence， traditional methods often only consider aleatory uncertainty， but epistemic uncertainty is rarely taken into account. This paper takes Brownian passage time (BPT) model as an example， epistemic uncertainty of mean recurrence interval of large earthquakes is analyzed quantitatively by using Bayesian estimation method， and how to take epistemic uncertainty into the calculation of the occurrence probability of large earthquake is also studied. The results show that there is significant difference in parameter uncertainty among different methods for determining mean recurrence interval of large earthquakes， also there is remarkable difference between the results with and without considering the epistemic uncertainty of parameters in the process of calculating the probability for large earthquake occurrence.

probability for large earthquake occurrence； parameter uncertainty； aleatory uncertainty； epistemic uncertainty

郭星， 潘华. 2016. 强震复发概率模型中的参数不确定性研究. 地震学报, 38(2): 298--306. doi:10.11939/jass.2016.02.013.

Guo X, Pan H. 2016. Parameter uncertainty analysis on probability model of strong earthquake recurrence.ActaSeismologicaSinica, 38(2): 298--306. doi:10.11939/jass.2016.02.013.

国家科技支撑项目(2012BAK15B01-08)资助.

2015-08-25收到初稿， 2015-11-02决定采用修改稿.

e-mail: panhua.mail@163.com

10.11939/jass.2016.02.013

P315.08

A