石油化工设备支承钢框架的稳定分析

刘洪

（中石化上海工程有限公司，上海 200120）

石油化工设备支承钢框架的稳定分析

刘洪

（中石化上海工程有限公司，上海 200120）

针对石油化工装置中支承设备钢结构框架较多存在布置不规则的特点，采用计算长度系数法、特征值屈曲分析、二阶分析法及高等分析法等，计算分析了框架的稳定性。通过各方法的对比，对此类钢框架的稳定设计提出一些有价值的建议。

稳定分析；计算长度；屈曲分析；二阶效应

石油化工装置中支承设备的钢结构框架由于受到工艺流程条件的限制，结构布置通常会出现不规则的特点，如：平立面布置不规则；荷载分布不均匀，结构刚度中心和荷载中心难以重合；结构重心较高，设备通常支撑于框架顶部并有较大水平推力等。上述特点使得此类框架的稳定问题相当突出，有必要进行专门研究。本文结合某工程实例，采用计算长度系数法、二阶分析，特征值屈曲分析、高等分析等方法，通过计算结果的比对，对支撑设备钢框架结构的稳定问题进行具体分析和研究。

某支撑设备的钢结构框架，纵向2跨为有支撑框架，跨度分别为4 m、3.45 m；横向单跨为无支撑框架，跨度为4 m；主要楼层有2层，底层为操作平台，2台设备支撑在顶层，设备设计荷载分别为400 t和200 t。相关布置图见图1、图 2。结构设计时由于受到相关专业的限制，轴线2底层柱子的强轴方向实际层高达到9 m；轴线3顶层框架梁由于设备布置要求需偏心布置，偏于安全考虑梁柱连接按铰接考虑。由于此构架位于一个大型装置中间，框架及设备不直接承受风荷载作用，因此计算时由地震组合控制，当地地震参数为：基本地震加速度为0.10 g，地震分组第二组，II类场地，设计特征周期为0.40 s，钢结构抗震等级为三级。

图1 结构三维图Fig.1 Structural space layout

图2 顶层平面图Fig.2 Top storey plan

1 计算长度系数法

1.1 规范计算长度系数法

在现行的工程设计中，为了便于实际应用，通

常采用计算长度系数法来验算框架的稳定。对框架进行稳定分析时，根据框架的失稳类型，利用弹性稳定理论求出柱的计算长度系数μ，乘以柱的几何长度后，得出柱的有效长度l0。此方法是将整体框架的稳定分析简化为单根框架柱的稳定计算。

钢结构规范（GB 50017—2003）[1]附录D给出了框架柱计算长度系数的计算方法：根据柱上下端横梁线刚度之和与柱线刚度之和的比值K1、K2，查附录D中表D-1、D-2求出计算长度系数μ。钢结构的稳定问题主要包括三个方面：平面内稳定、平面外稳定和构件的局部稳定。对于钢框架，通过设置竖向支撑来解决平面外稳定问题，构件的局部稳定则通过截面构造来解决，因此本文只比较了框架的平面内稳定的计算长度系数及长细比数据。

图3 框架立面尺寸及柱子编号Fig.3 Frame elevation detail and column number

根据规范方法计算的各框架柱的计算长度系数及其长细比结果见表1、表2。从图3可见轴线2的底层柱K21由于跨层，柱计算长度l0=3.57×9=32.13 m，长细比达到129.5。根据《建筑抗震设计规范》规定，对于三级框架，Q235的框架柱的长细比限值为100。柱K21、K33已超出规范20 % ～ 30 %，需要加大框架柱截面。

表1 框架柱强轴方向的计算长度系数μTab.1 Column effective length coefficient μ

表2 框架柱强轴方向的长细比Tab.2 Column slenderness ratio

计算长度系数法的主旨就是将构件之间的相互作用通过计算长度来反映，将单个构件的成熟理论应用于框架的整体设计。但是由于计算长度系数法是一种简化的计算方法，计算长度的取值对于结构设计的安全性和经济性有着直接的影响，因此需要在不断的研究中加以完善。

1.2 考虑整体失稳对计算长度系数的修正方法

对于无支撑有侧移框架，结构失稳是一种整层的失稳，规范的计算长度系数法是确定单根柱子的稳定性，不能反映框架整体失稳时的真实情况。钢结构框架的稳定设计实质就是对结构抗侧刚度的设计。

框架的抗侧刚度为零时，框架整体失去稳定，结构转变为机动体系或整体倾覆。对计算长度系数法的使用中，整体和构件的稳定设计都通过计算长度系数来反映。童根树等[2]通过引入D值法研究证明计算长度系数的另一个含义：它反映的是柱子的抗侧刚度系数，在此基础上进一步引入轴力负刚度的概念，当结构抗侧刚度小于轴力负刚度时发生有侧移失稳。文献[2]、[3]通过D值法在考虑了同层各柱子间相互支援作用后，给出了计算长度系数的修正公式（1）。

式中 μi' ——修正后的计算长度系数；

Ici——柱的截面惯性矩；

Pi——柱轴力；

hj——层高；

αj—— 竖向荷载与柱局部弯曲变形产生的二阶效应对侧向刚度的影响系数；

μj—— 按规范计算的长度系数。

根据公式（1）对表1中的原计算长度系数μ进行修正，结果见表3、表4。由于考虑了同层其它柱子的贡献，原长细比超限的柱K21、K33在修正后满足规范要求，同时其余柱子的长细比有所增大。

表3 框架柱强轴方向的计算长度系数的修正值μi' Tab.3 Column effective length coefficient modification μi'

表4 框架柱强轴方向修正后的长细比Tab.4 Column slenderness ratio modification

规范计算长度系数法计算时，假定框架中所有柱子是同时失稳的，即每根柱同时达到其临界荷载。而修正方法对此假定做了一定的修正，考虑了结构失稳时同层内各柱的协同作用，使得柱子的计算长度系数减小，承载能力得以提高。

2 特征值屈曲分析法

屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷，屈曲分析包括线性屈曲和非线性屈曲分析。线性屈曲分析即特征值屈曲分析，就是用结构的材料刚度矩阵减去荷载作用下的结构的几何刚度乘以一个系数，当总刚度矩阵奇异时就是失稳特征值。特征值屈曲分析适用于对一个理想弹性结构的理想屈曲强度（岐点）进行预测，主要是使用特征值公式计算造成结构负刚度的应力刚度阵的比例因子[4]。虽然特征值屈曲分析方法只适用于理想结构，并未考虑结构非线性和初始缺陷的影响，但由于其计算相对简单，可以先用其分析了解屈曲形态，然后再根据公式（2）[5]来确定柱的计算长度系数。

式中 γ ——屈曲荷载因子；

Ni——柱轴力；

E ——钢的弹性模量；

Ici——柱的截面惯性矩；

μi——柱的计算长度系数；

hi——柱子长度。

计算时采用恒载与活载的荷载组合，通过框架整体屈曲分析求出第1、2阶的屈曲模态，见图4，前几阶的屈曲荷载因子见表5。

通常情况下第一阶的屈曲模态对应的计算长度最为不利，将第一阶的屈曲荷载因子3.651代入公式（2）求得的计算长度系数结果见表6，得出的长细比与1.2节的计算长度修正法相比，第一层相近，而第二层相差较大。

特征值屈曲分析不需要复杂的计算过程，可以用于对结构稳定承载力进行初期的预测；也可以用于得到结构的屈曲模态，为后期非线性稳定分析提

供结构初始几何缺陷分布。但是它是纯理论的理想结果，偏于不安全，一般情况下不直接应用于实际工程设计。

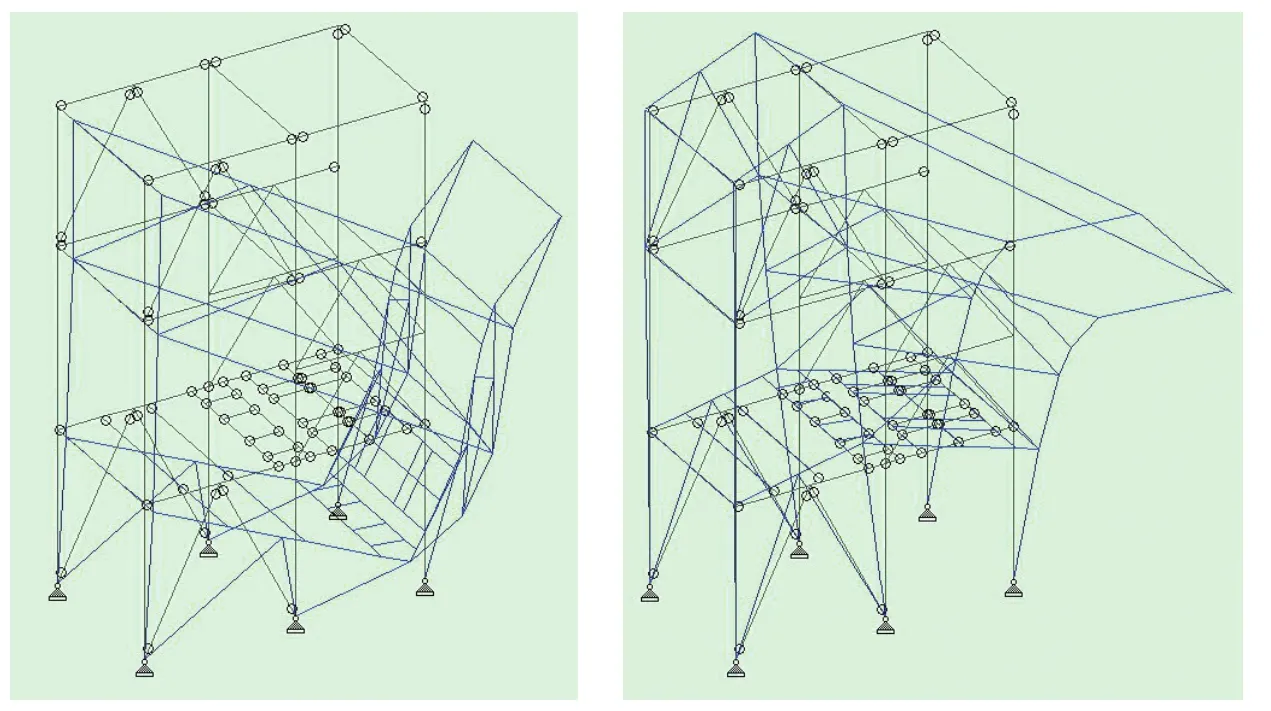
图4 第1，2阶屈曲模态Fig.4 No.1&2 buckling model

表5 屈曲荷载因子γTab.5 Buckling load gene γ

表6 框架柱强轴方向的计算长度系数μTab.6 Column effective length coefficient μ

3 二阶分析法

框架稳定分析时，除了常用的一阶分析，必然要涉及到框架结构的位移和位移对内力产生的影响，即二阶效应。二阶分析法就是考虑结构二阶变形对内力产生的影响，根据位移后的结构建立平衡条件。因此，对待框架结构的稳定问题，原则上都应采用二阶分析。

现行《钢结构设计规范》提出：对于满足公式（3）的框架结构宜采用二阶弹性分析，此时应在每层柱顶附加考虑由公式（4）计算的假想水平力。假想水平力Hni是用来考虑结构初始缺陷的影响。稳定计算时框架柱的计算长度系数取1.0，对于稳定计算，如果内力采用二阶分析方法确定，又考虑了初始缺陷，那么只要进行强度计算即可，无需再进行稳定验算。但是考虑到规范的二阶分析方法是近似的，仅考虑了有侧移的P-Δ效应，而没有考虑无侧移的P-δ效应，而且初始缺陷的影响无法真实模拟，为了安全起见，规范仍取计算长度系数为1.0进行稳定计算[6]。

式中 ∑N —— 计算楼层各柱轴心压力设计值之和；

∑H—— 产生层间侧移Δu的所计算楼层及以上各层的水平力之和；

Δu —— 按一阶弹性分析求得的所计算楼层的层间侧移；

h ——计算层高。

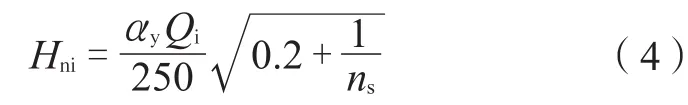
式中 Qi——第i层的总重力荷载设计值；

αy—— 钢材强度影响系数，对本例Q235钢取1.0；

ns——框架总层数。

规范二阶分析法的计算结果详见应力比汇总表7。由于柱的计算长度系数取1.0，所以计算长度系数及长细比的相关数据不再罗列。

4 高等分析法

为了进一步分析框架的稳定性，验证上述方法的适用性，对框架整体进行二阶非线性弹塑性有限元分析。计算时考虑的结构初始缺陷包括构件的残余应力和初弯曲、结构的初始偏心。残余应力是结构构件的主要初始缺陷，也是影响构件极限承载力和弹塑性刚度的重要因素。对于构件的稳定计算，各国都有自己的残余应力统计资料，本文主要参考了欧洲钢结构协会[7]（ECCS）推荐的截面残余应力分布模式，如图5、图6。

图5 热轧H型钢Fig.5 Hot-rolled H section steel

图6 焊接H型钢Fig.6 Welded H section steel

框架柱顶点侧倾缺陷根据施工容许偏差，取结构层高的1 / 500计算，缺陷方位统一取框架强轴方向；构件的初始弯曲取构件长度的1 / 1 000，见图7所示。

图7 结构初倾斜及构件的初弯曲Fig.7 Structural initial displacement

图8 荷载因子与位移曲线Fig.8 Load gene and displacement curve and member initial curvature

图8为荷载因子与位移曲线，从曲线可知，框架的极限承载力约为1.33倍的设计荷载。由于高等分析采用的材料是标准值，需要乘以0.9折算为设计值。因此高等分析计算的框架极限承载力为1.2倍的设计荷载。

5 结果汇总与分析

5.1 应力比

采用上述各计算方法对框架进行一阶或二阶分析，框架各柱的应力比结果详见表7。

根据表7和图8可知，高等分析计算的框架承载力结果与规范的二阶弹性计算最为接近，其极限承载力约为二阶分析法的1.1倍。计算长度系数法的极限承载力最小，由于轴线2下柱K21计算长度达到32.13 m，弯矩作用平面内轴心受压构件稳定系数φx= 0.44，使其最先达到极限状态，应力比为1.14，此时其余各柱的承载能力还有30 % ～ 60 %的富余量。

计算长度修正后的计算结果和屈曲分析相近，各柱的承载能力偏于不安全。

表7 框架各柱的应力比Tab.7 Frame column stress ratio

计算长度系数法是在一些理想化假定的基础上独立计算每根柱子，当其中某根柱子失稳时，框架即达到其极限状态，计算结果偏于保守；二阶分析法是整体分析的方法，考虑了框架的整体变形协调，能够更为精确地考虑变形对结构的影响，更能体现结构的真实受力情况，其精度和安全性可以满足工程设计的需要；计算长度修正法由于计算框架的布置不规则，无法在每层的平面内形成足够的刚度，过高估计了结构的平面刚度造成其计算结果偏于不安全，文献[3]证明此方法对于较为规则的结构能取得比较准确的结果；特征值屈曲分析是在理想化状态下的计算结果，是屈曲荷载的上限值，不应直接用于实际工程设计。

5.2 顶点位移

由于框架考虑二阶效应，计算后的位移值会明显大于一阶分析，这就可能会出现一阶位移满足规范要求，而二阶位移却不能满足的情况。此时，为满足规范要求，需要加大构件截面，如因采用二阶分析，却要增加用钢量，这不尽合理。表8给出了框架一阶分析与二阶分析的位移结果的比较，二阶效应引起的顶点位移增量最大达到37 %。

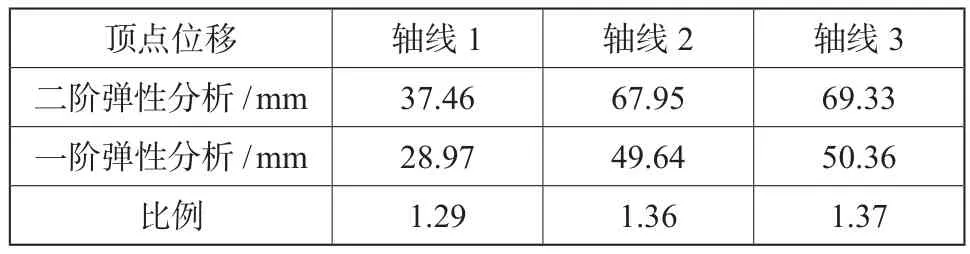
表8 一阶、二阶框架顶点位移对比Tab.8 Comparison of first order and second order displacement

文献[8]结合规范的二阶分析方法及可靠度理论，对于钢框架结构二阶层间侧移限值给出了参考意见，其限值约为规范一阶时的75 %。对二阶分析的位移限值的研究使得二阶分析法更具有实际使用价值，提高了材料的使用效率。综合上述研究表明本框架顶点位移能够满足要求，截面选择合理。

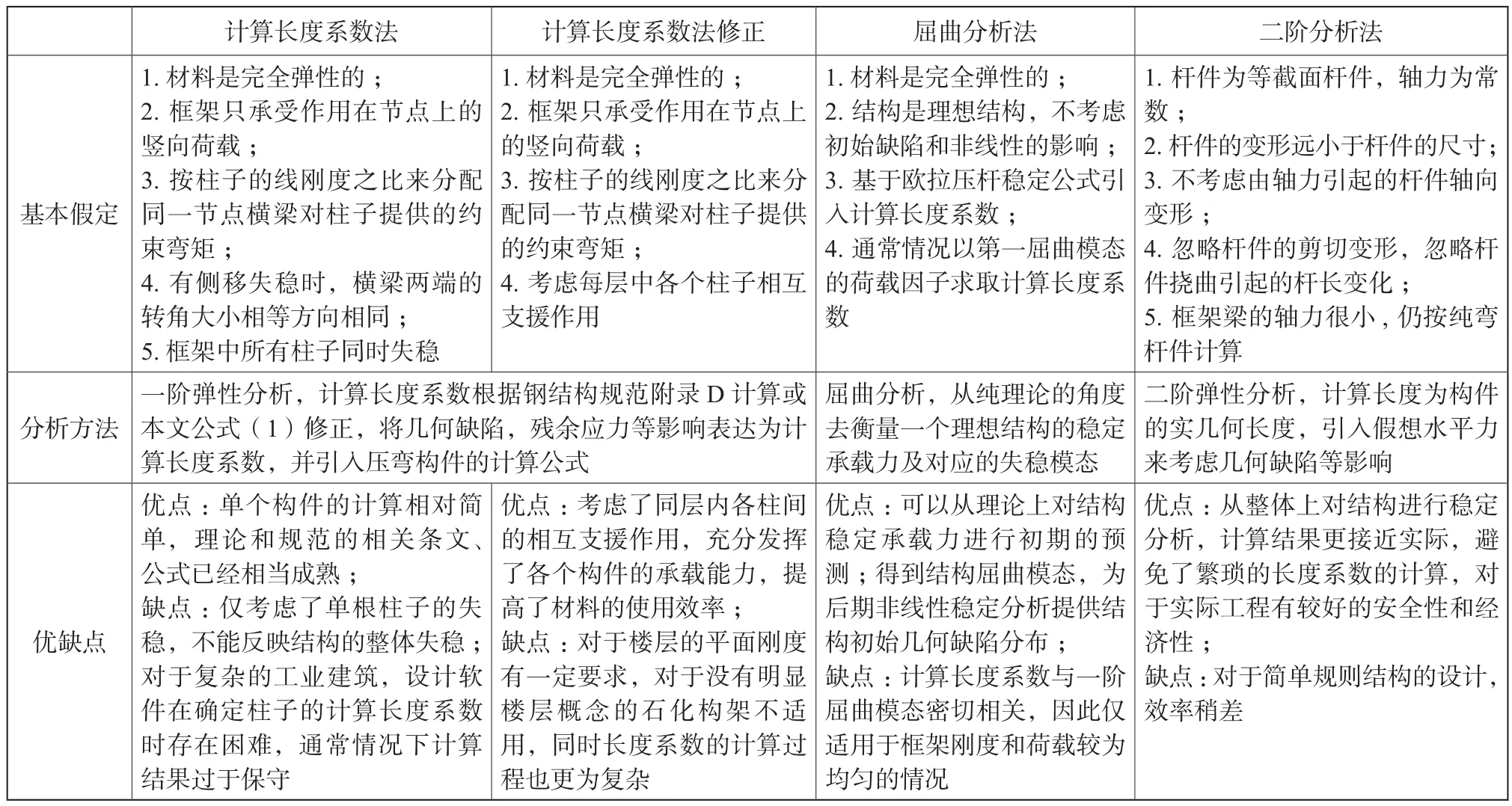
表9 稳定计算方法对比Tab.9 Comparison of stability analysis method

5.3 各方法比较

通过对框架计算结果的分析，表9从三个方面

对各种稳定计算方法进行比较。

6 结束语

对于石化项目中常见的支撑设备的钢框架结构，由于结构布置通常不规则，计算长度法本身的假定缺陷有可能造成计算结果失真。整层失稳的计算长度系数修正法不适合平立面不规则的框架，屈曲分析也存在类似问题，此时就有必要采用直接反映框架二阶效应的分析方法。现阶段精确的二阶非线性弹塑性分析建模和计算较为复杂，不便应用于工程设计，宜采用规范推荐的近似二阶分析法，同样能较好地满足实际工程设计的精度和安全性。在实际工程设计中需要注意，考虑二阶效应后，框架结构的位移会增大，具体影响与结构形式、刚度、荷载作用的大小和分布等因素有关，应综合评价其影响。

[1]GB 50017—2003 钢结构设计规范[S].

[2]童根树，施祖元，李志飚.计算长度系数的物理意义及对各种钢框架稳定设计方法的评论[J].建筑钢结构进展，2004，6（4）：1-8.

[3]童根树.钢结构的平面内稳定[M].北京：中国建筑工业出版社，2005.

[4]王晨广.施威德勒椭球形弦支穹顶的特征值屈曲分析[J].四川建筑，2011，37（3）：26-30.

[5]童根树，饶芝英.一个奇特的除尘器钢支架的屈曲问题[J].建筑钢结构进展， 2007，9（5）：42-46.

[6]童根树，金阳.框架柱计算长度系数法和二阶分析设计法的比较[J].科研开发，2004，20（2）：8-11.

[7]ENV 1993-1-1 Eurocode 3：Design of Steel Structure Part1.1：General rules for Buildings[S].

[8]舒兴平，邹浩，卢倍嵘，等.钢框架考虑二阶效应的层间侧移限值取值及可靠度分析[J].建筑结构学报，2011，32（8）：113-119.

《化工与医药工程》征稿启示

《化工与医药工程》（CN31－2101/TQ）（原《医药工程设计》）创刊于1980年，是经国家科技部、国家新闻出版广播电影电视总局正式批准，面向国内外公开发行的专业技术期刊，是国家评定的学术期刊（A类）。由中国石油化工集团公司主管，中石化上海工程有限公司主办。

本刊征稿的具体范围为：

化工工艺与工程、医药工艺与工程、装备应用与研究、HSE与节能减排、综述与专论等。

本刊对稿件的录用以技术和质量为主导，不收取作者的审稿费和版面费，亦从无委托任何机构或个人收取相关费用。欢迎各高校、工程公司、设计院、生产企业等师生、技术人员投稿。

来稿要求详见第53页《化工与医药工程》投稿指南。

投稿邮箱：cpe.ssec@sinopec.com

常务副主编邮箱：kebao666@126.com chenkebao.ssec@sinopec.com

Stability Analysis of Steel Frame Used in Supporting Petrochemical Equipment

Liu Hong
（SINOPEC Shanghai Engineering Co., Ltd, Shanghai 200120）

With respect to the features that steel frame in petrochemical plant are often irregularly arranged, by using effective length coefficient buckling analysis, eigenvalue buckling analysis, second order analysis and accuracy analysis, the stability of steel frame were calculated and analyzed. With the comparison of the results from various analysis methods, some proposals for stability design of steel frame were presented.

stability analysis; effective length; buckling analysis; second order effect

TU 391

A

2095-817X（2016）05-0040-007

2016-07-11

刘洪（1983—），男，工程师，主要从事石油化工结构设计工作。