一道常见数列题引发的思考

●刘其梅

(霍邱县第一中学 安徽霍邱 237400)



一道常见数列题引发的思考

●刘其梅

(霍邱县第一中学 安徽霍邱 237400)

数列是高中数学的重要内容，虽然经历了多次课改，但它在高中数学中的地位从未动摇，在高考中所占的比重一直都较大.因为与数列有关的题目尤其是大题，综合性较强，难度较大，所以很多学生都惧怕数列题.若能掌握一些解决技巧，则能使题目简化，使运算简洁优美，从而大大提高了解题速度.

笔者从一道常见数列题求和的角度，引发不被人们所关注的数列——常数列的思考，探寻常数列在解多种题型中的巧妙应用，感受其优美.

例1 数列{an}满足an=n·3n，求数列{an}的前n项和Sn.

解法1 由Sn=1·3+2·32+3·33+…+n·3n,知

3Sn=1·32+2·33+3·34+…+n·3n+1.

2个式子相减可得

-2Sn=1·3+1·32+1·33+…+1·3n-n·3n+1,

从而

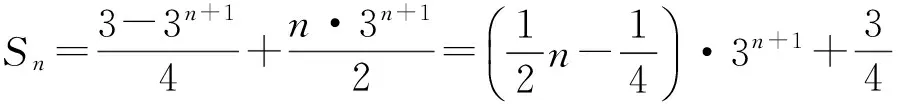
解法2 因为an=n·3n，所以Sn-Sn-1=n·3n，经配凑可得

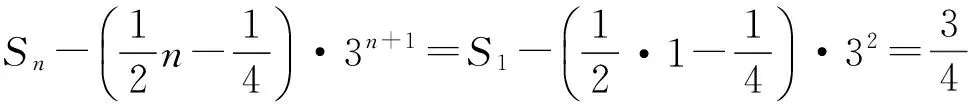
故

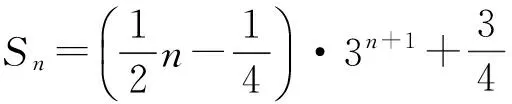
解法1是我们常用的一种方法——错位相减法，该解法计算量较大，过程较繁杂，在应用的过程中容易出错.解法2通过配凑后得到一个常数列，利用常数列各项都相等的特点很轻松就得到了数列{an}的前n项和.因此，只要掌握了“配凑”技巧，解法2明显优于解法1.通过本例，读者是不是与笔者一样看到了常数列的神奇，是不是也喜欢上了它？下面笔者从4个方面阐述常数列在解数列题中的神奇妙用.

1 常数列在数列求和中的妙用

分析 仿照例1的解法，构造常数列来解决此题的求和问题，难点在于如何“配凑”，可尝试用待定系数法进行配凑.

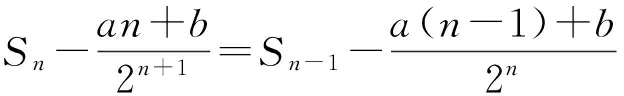
2个式子比较可得

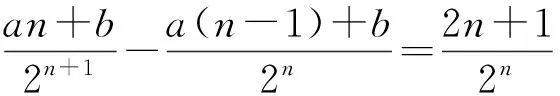
等式2边比较可得a=-4,b=-10，于是

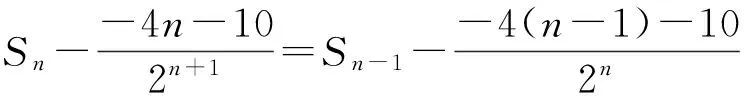
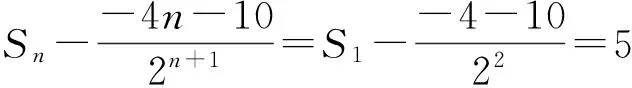
故

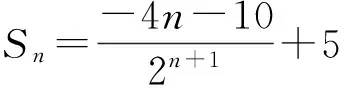
此题中用待定系数法解决了“配凑”这一难题之后，就可以借助神奇的常数列，把复杂的数列求和问题转化为简单的求和问题，从而减少了运算量，降低了出错率.

例3 数列{an}满足an=n2·2n，求数列{an}的前n项和Sn.

分析 此题中2n前面的数为n2，因此在配凑时要注意2n前面的数的次数不再是一次而是二次.

解 因为an=n2·2n，所以Sn-Sn-1=n2·2n，将其配凑变形，可设

Sn-(an2+bn+c)·2n+1=Sn-1-[a(n-1)2+b(n-1)+c]·2n，

可得

(an2+bn+c)·2n+1-[a(n-1)2+b(n-1)+c]·2n=n2·2n,

化简得

(an2+bn+c)·2-[a(n-1)2+b(n-1)+c]=n2.

等式2边比较可得a=1,b=-2,c=3，从而

Sn-(n2-2n+3)·2n+1=Sn-1-[(n-1)2-2(n-1)+3]·2n，

于是数列{Sn-(n2-2n+3)·2n+1}是常数列，因此

Sn-(n2-2n+3)·2n+1=S1-(12-2·1+3)·21+1=-6，

故

Sn=(n2-2n+3)·2n+1-6.

2 常数列在求数列通项公式中的妙用

“已知数列的递推公式，求数列的通项公式”是难点，解决此类问题往往需要较强的观察分析力，找出递推公式的特点，剖析其中的关系.而在解题过程中，若能应用好常数列，则能事半功倍，优化解题.

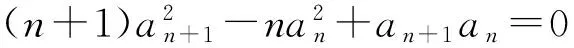
解法1 已知条件可转化为[(n+1)an+1-nan](an+1+an)=0.又an+1+an>0，则

(n+1)an+1-nan=0，

从而

(n+1)an+1=nan，

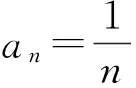
对于本题的解法，平时我们往往用的是“累乘法”：

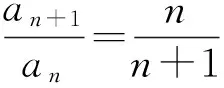
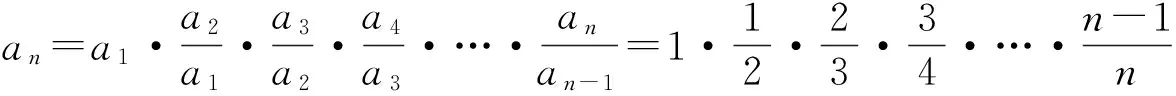
姑且不问这2种解法哪种更简洁，但显然解法1给我们耳目一新的感觉,在解法1的解题过程中，只需观察出数列是常数列后，一切问题都迎刃而解了.

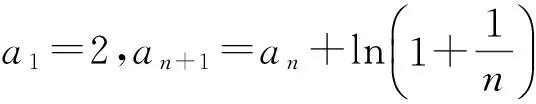
an+1-ln(n+1)=an-lnn，

从而数列{an-lnn}为常数列，于是

an-lnn=a1-ln1=2，

故an=lnn+2.

同例4一样，该题平时解决的主要方法是“累加法”：

an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+(ln2-ln1)+(ln3-ln2)+…+[lnn-ln(n-1)]，

化简得

an=lnn+2.

从例4和例5可以看出，平时用“累加法”、“累乘法”解决的问题，也能通过构造常数列来解决，而且过程显得更加简洁.下面继续来看常数列在求通项公式中的应用.

例6 在数列{an}中，a1=3，an+1=2an+1，求数列{an}的通项公式.

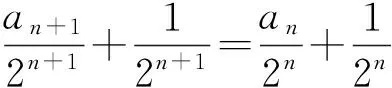
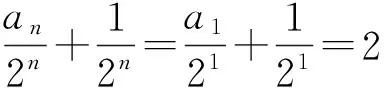
故

an=2n+1-1.

解得λ=1，从而

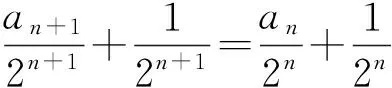
例7 在数列{an}中，a1=1，an+1=2an+2n+1，求数列{an}的通项公式.

解 因为an+1=2an+2n+1，2边同除以2n+1，得

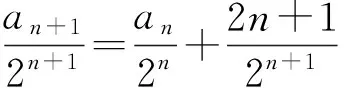
此式可变形为

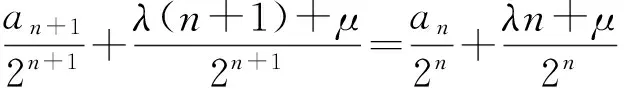
2个式子比较可得

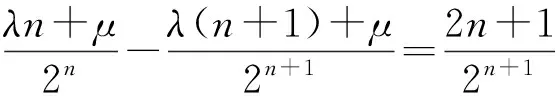
解得λ=2,μ=3，从而

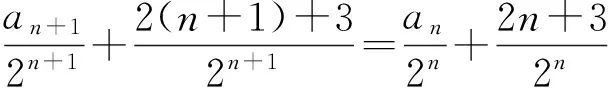
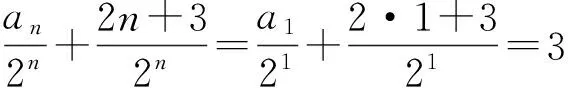
因此

an=3·2n-2n-3.

本题的方法可用来解决形如an+1=pan+qn+m(其中p,q,m为常数)型求通项问题.

例8 在数列{an}中，a1=1，an+1=3an+2n，求数列{an}的通项公式.

解 因为an+1=3an+2n，2边同除以3n+1，得

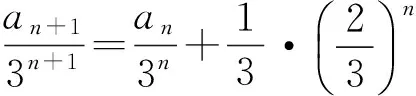
此式可变形为

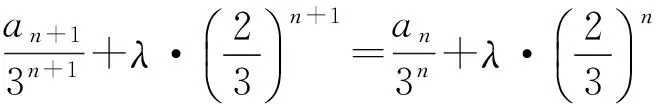
2个式子比较可得

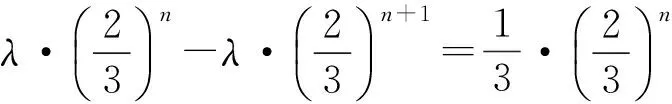
解得λ=1，从而

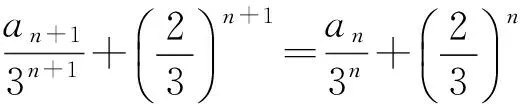
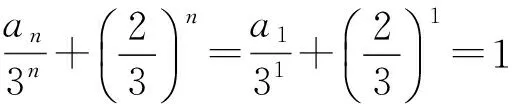
本题的方法可解决形如an+1=pan+qn(其中p,q为常数)型求通项问题.

其实，在已知数列的递推公式求数列通项公式的过程中，我们可以观察数列的递推公式，注意数列第n项和第n+1项的联系和差异，对数列的递推公式进行变形，使含有an组合数列的第n项和第n+1项相等，即构造出常数列，求出常数列的通项公式后即可以巧妙地求出an.

3 常数列在证明恒等式中的妙用

解 构造数列{an}，使

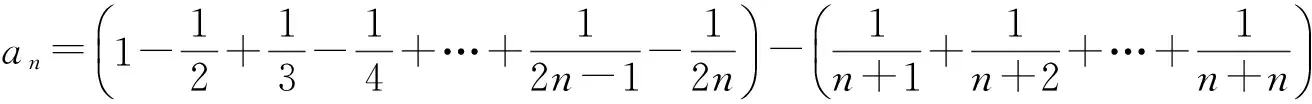
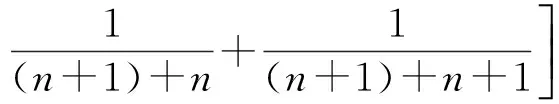
从而

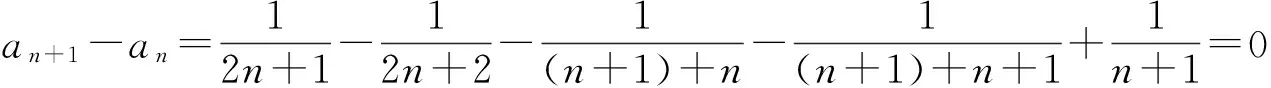
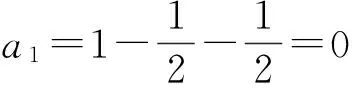
例10 求证：(n+1)(n+2)(n+3)…(n+n)=2n·1·3·…·(2n-1)(其中n∈N*).

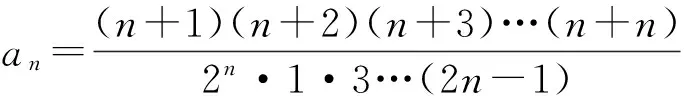
从而数列{an}为常数列，故an=a1=1.

4 常数列在解有关数列选择题、填空题中的妙用

例11 在等差数列{an}中，若a4+a6=12，Sn是数列{an}的前n项和，则S9的值为

( )

A.48 B.54 C.60 D.66

解 因为a4+a6=12且{an}为等差数列，所以a5=6，因此可设{an}为常数列.可取an=6，则S9=9·6=54.故选B.

例12 已知数列{an}的前n项和Sn满足：Sn+Sm=Sn+m，且a1=1，则a10=

( )

A.1 B.9 C.10 D.55

解 若设数列{an}为常数列，且an=1，则Sn=n,Sm=m,Sn+m=n+m，有Sn+Sm=Sn+m，满足题意，从而a10=an=1.故选A.

例13 在等比数列{an}中，a1=2，前n项和为Sn，若数列{an+1}是等比数列，则Sn=______.

解 因为数列{an}为等比数列且数列{an+1}也是等比数列，所以可构造常数列{an}，使an=2，满足题意，从而Sn=2n.

实际上，我们在解决有关数列的选择题、填空题的过程中，可以巧妙应用数列的性质，进行大胆猜测、验证；构造特殊的常数列，使问题解决得简洁、精巧、明快，达到出奇制胜的效果.

总之，解答数学题的关键还在于要掌握思考问题的方法.对于同一类型的题目，可以从不同的角度去观察思考.由于观察角度的改变，就可以寻找到解决问题的更佳途径，使问题变得更加简单，使解题过程大大简化，达到事半功倍的效果.常数列作为数列中最特殊的数列，平时往往得不到重视，更谈不上对它的应用了.希望大家能从本文得到启示，在以后解数列题的过程中，多变换观察题目的角度，构造满足题意的常数列，它或许就是你解决问题的“钥匙”.