基于最大似然的网络拓扑推断技术研究（一）

王 黎，张润生

（中国电子科技集团公司第五十四研究所，石家庄 050081）

Technology Study

基于最大似然的网络拓扑推断技术研究（一）

王 黎，张润生

（中国电子科技集团公司第五十四研究所，石家庄 050081）

本文针对基于主动探测的网络拓扑推断问题，提出了基于广义似然比的拓扑推断技术，仿真结果表明，该算法有较高的拓扑推断精度。

网络分析；拓扑结构；拓扑推断；最大似然

1 引言

本文以网络拓扑探测为出发点，将网络限定为规模较小的IP网络，假设探测节点已接入目标网络，探讨此情景下基于最大似然的网络拓扑推断问题。提出了一种基于子树序贯合并的网络拓扑推断算法，首先将每个叶子节点都作为一颗子树，由最大似然算法估计各个子树之间的相关性，取其中相关性最大的两颗子树；然后应用广义似然比假设检验算法来判断两子树的合并方式并对其进行合并；接着对合并后的子树集合重复以上过程直至子树集合中只有一颗树为止。该算法使用似然比方法合并子树，无需设置惩罚参数，具有更高的稳健性。

2 拓扑推断模型

树状网络拓扑可建模为有向逻辑树[8，9]T，令T=(V,E)，V为树中的顶点集合，对应于网络中的主机、路由器等，V由根节点s、叶子节点集合D（其叶子节点个数为Nr=|D|）以及内部节点集合I构成；E为边集合，对应于网络中的通信链路。令树根节点s为源节点，树的叶子节点集合D为接收节点。令U=sUD为端节点，易得U中所有节点的度都为1（假设每个端节点仅与一个路由器相连）。该逻辑树[10]中除根节点之外的所有非叶子节点均至少有两个孩子节点，除根节点之外的所有节点v∈IUD均有惟一的父节点f(v)；令(f(v),v)，f(v)，v∈V表示v与其父节点之间的链路；令(s,v)为根节点s与节点v之间的链路；令a(i,j),i≠j,i,j∈D为节点对{i,j}最深（距根节点最远）的公共父节点，可见a(i,j)为源节点s到节点对{i,j}的分支节点；令p(i,j)为{(s,i),(s,j)}的共享链路，即P(i,j)=(s,a(i,j))。

定义叶子节点的相关性为γij=￥(P(i,j))，￥(P(i,j))表示节点对{i,j}共享链路上的某种性能的度量（排队时延方差、丢包率方差等），满足￥(P(i,j))∝P(i,j)，可见拓扑树中叶子节点对的共享链路越长，相关性越大。叶子节点相关性满足以下条件[8]：

（1）单调性：如果P(i,j)是P(k,l)的子链路，其中，i,j,k,l∈D且i≠j,k≠l，则有γij＜γkl。

（2）一致性：如果P(i,j)与P(k,l)为相同链路，即a(i,j)=a(k,l)，其中，i,j,k,l∈D且i≠j,k≠l，则γij=γkl。

定理1：集合A={γij,a(i,j)=p;i,j∈D;i≠j}与集合B={γik,a(i,k)=q;i,k∈D;i≠k}中元素数值相等的充要条件是内部节点p和节点q为树状拓扑中的同一内部节点，即p=q。

证明：由于集合A中元素都是具有相同父节点的叶子节点之间的相关性，因此A中各个元素数值相等，同理B中各个元素的数值也相等，因此要证明A与B中各个元素的数值都相等，只需证明γij=γik即可。首先证明充分性，p=q即a(i,j)=a(i,k)表明由源节点s到节点对{i,j}的共享链路(s,a(i,j)与s到节点对{i,k}的共享链路(s,a(i,k))为同一链路，又由于节点相关性的大小由节点对的共享链路长度决定，因此可得γij=γik。再证明必要性，反证法，假设γij=γik，p≠q，即a(i,j)≠a(i,k)，由于p，q分别为源节点s到{i,j}和{i,k}的分支节点，那么p，q都位于链路(s,i)上，又由于p≠q，则链路(s,p)的长度不等于链路(s,q)的长度，即由源节点s到节点对{i,j}的共享链路(s,a(i,j))的长度与s到节点对{i,k}的共享链路(s,a(i,k))的长度不相等，那么可得节点对{i,j}的相关性不等于节点对{i,k}的相关性，即γij≠γik，与假设γij=γik矛盾，因此若γij=γik必有p=q，证毕。

图1 树状拓扑示意图

性质1[8]：在节点相关性测量过程中网络的统计特性平稳的条件下，根据叶子节点相关性的一致性

推论1：内部节点p和节点q为树状拓扑中的同一内部节点（即p=q）的充分条件是

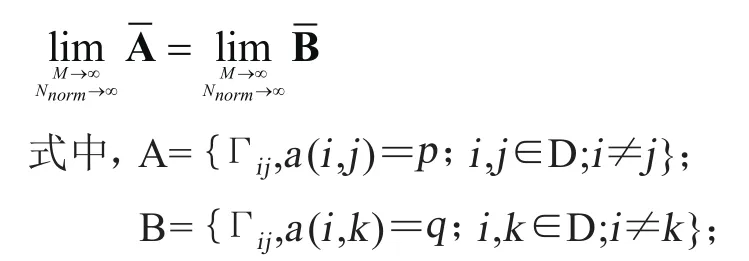
证明：易得M→∞，Nnorm→∞时，

由推论1可得，我们可以通过检验集合A与B的均值是否相等来判断拓扑中内部节点p和q是否为同一节点，本文算法正是基于这一思想来判断子树的合并方式。

3 基于似然比的子树合并的拓扑推断算法

本节基于广义似然比检测通过对子树序贯合并来推断树状拓扑。文献[6，9]应用了节点合并的方法推断拓扑，但其找到最相关子树之后都按照二叉树来合并，这显然与真实情况相去甚远。本算法的创新之处在于：分析了最相关子树的各种可能的合并方式；提出了基于广义似然比检测的子树合并方式判定方法。

3.1 子树合并

3.1.1 寻找最相关子树

首先给出子树相关性的定义，任取两颗子树Ti，Tj，二者的叶子节点集合分别为U和V，叶子节点个数分别为K，L，则子树Ti与Tj之间的相关性定义为

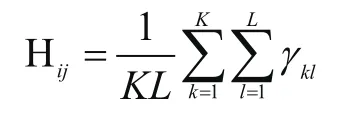
式中，γkl为子树Ti中的叶子节点k与子树Tj中的叶子节点l的相关性。

定理2：如果序贯合并过程中每次选择的两棵子树{Ti,Tj}均为最相关子树，则每次子树合并的合并点（两树合并的接触点）在合并后的树中仅可能体现为原子树的根节点或者原子树根节点的父节点。其中合并点是为合并两颗子树而创建的新节点，如图2中节点q。

证明：反证法，不失一般性，我们假设两子树的合并点为左子树Ti根节点的孩子节点，如图2所示，实线表示左子树Ti，虚线表示右子树Tj，两子树合并点为q，则q为左子树根节点i的孩子节点，那么此时从源节点s到节点i的链路长度要小于从源节点s到节点q的链路长度，则可得（1）：子树b与子树j的相关性大于子树a和子树b的相关性；而又由于序贯合并过程中每次选择的子树对{i,j}均为最相关子树，则可得（2）：子树b与子树j的相关性小于子树a和子树b的相关性。显然（1）与（2）矛盾，因此如果满足序贯合并过程中每次选择的子树对{i,j}均为最相关子树，则每次子树合并的合并点必为子树的根节点或者子树根节点的父节点，而不可能是两棵子树根节点的孩子节点。

图2 子树合并示意图

给定子树集合{Tl,l=1,…L}，任取其中两颗子树Ti，Tj，二者的叶子节点集合分别为U和V。子树Ti所有叶子节点与Tj所有叶子节点之间的相关性集合为Γ＝｛γuv，u∈U，v∈V }，u，v分别为子树Ti与Tj的叶子节点。由于对于任意u和v，在其待推断的真实拓扑中具有相同的最深父节点，所以由定理1得，集合Γ中所有元素都有相同的数值，定义这个数值为子树之间的相关性γij。根据性质1，我们可以认为子树Ti任意叶子节点u与Tj的任意叶子节点v之间的相关性采样值，n=1,…,N，都服从相同的高斯分布N(γij,σ2)，因此可根据（1）式估计Ti，Tj的相关性

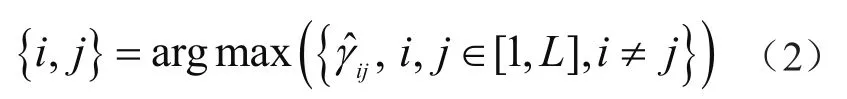
3.1.2 子树合并方式

在找到最相关子树对之后，需要判定子树的合并方式。两个子树的合并可分为三种情况，1）叶子节点数目均为1的两子树合并；2）叶子节点个数为1的子树与叶子节点数不为1的子树的合并；3）两个叶子节点数目都不为1的子树的合并。

由定理2可得，在情况1）中子树的合并方式仅有一种，如图3所示；情况2）中子树有四种可能的合并方式如图4所示；情况3）中子树也有四种可能的合并方式，如图5所示。图中叶子节点数不为1的子树由有两个叶子节点的树代表，实线表示左子树，虚线表示右子树。

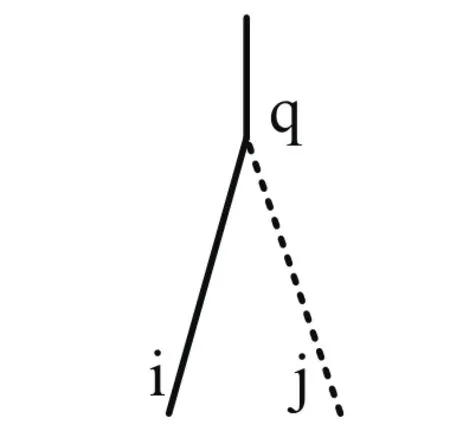
图3 情况1的合并方式

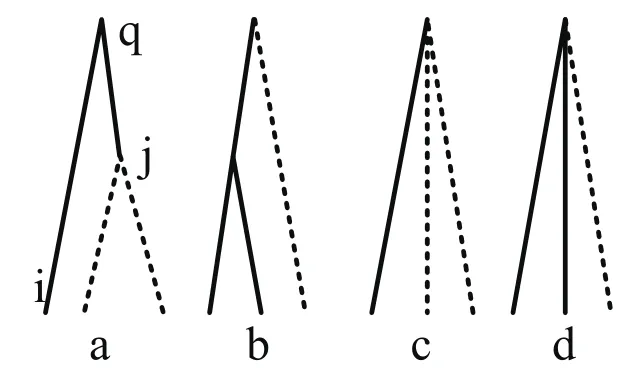
图4 情况2的合并方式

图5 情况3的合并方式

设左右子树的根节点分别为i和j，合并点为q，我们只需确定i，j，q中哪些点为相同的节点，即可推断出子树以哪一种方式合并。对于情况1）只有一种合并方式；对于情况2）只需判断节点数不为1的子树的根节点是否与合并点q为相同的节点即可；对于情况3）我们需要判断两个子树的根节点是否与合并点q为相同的节点。例如在情况3）的a方式（图5）中i，j，q三个节点为不同的节点；b中i，q两点为相同节点，j为独立的节点；c中j，q为相同的节点，i为独立的节点；d中i，j，q三个节点为相同的节点。表1给出了情况3）子树合并与i，j，q节点之间关系的映射。

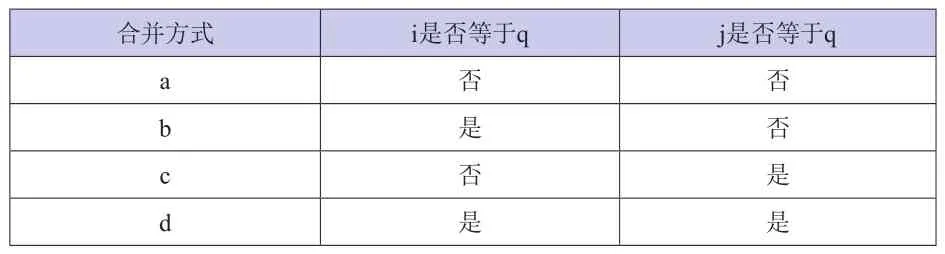
表1 合并方式映射关系

接下来，我们只需确定i，j，q三个节点的关系即可判定出子树合并方式。由于序贯合并过程中满足每次选择的子树对{i,j}均为最相关子树，则结合定理2，可得合并点q的等价定义：设左右子树的叶子节点集合分别为K，L，∀k∈K，∀l∈L，满足a(k,l)=q。则可得节点q对应的叶子节点相关性集合为C=｛,a(k,l)＝q；k∈K；l∈L}。i,j对应的叶子节点相关性集合分别为A=｛,a(m,n)＝i；m,n∈K;m≠n}，B=｛,a(u,v)＝j；u,v∈L;u≠v}。由推论1，我们可知，通过比较集合A，B，C的均值即可判定i，j，q三个节点的关系，进而根据表1中的映射关系获得子树的合并方式。

我们采用广义似然比的方法比较集合A，B，C的均值。

由于对于原始待推断树状拓扑，其叶子节点之间相关性的相对大小关系是确定的（因为要满足单调性和一致性），那么在理想情况下叶子节点相关性的测量值的相对大小也满足此确定关系，因此，只要保证推断出的树状拓扑中由叶子节点共享链路长度表征的叶子节点相关性的相对大小关系，与实际中测得的叶子节点相关性的测量值的相对大小关系一致，即可认为推断出的拓扑就是待推断的拓扑。分析我们的推断过程，由于使用最相关子树合并，因此在推断过程中保证了相关性测量值较大的叶子节点之间的共享链路长度大于相关性测量值较小的叶子节点之间的共享链路长度，且合并过程中使用了合适的合并方式，保证了共享链路长度相等的叶子节点有相同的公共父节点，那么我们可得由最相关子树合并方法推断出的保留了叶子节点相关性的相对大小关系，其推断出的拓扑就是原始拓扑。（未完待续）

[1] DONNET D,FRIEDMAN T.Internet topology discovery:a survey[J].IEEE Communications Surveys and Tutorials,2007,9(4):2-15.

[2] ZHANG X,CHRIS P.A survey on selective routing topology inference through active probing[J].IEEE Communications Surveys &Tutorials,2012,14(4):1129-1141.

[3] 姜誉，方滨兴，胡铭曾．．大型ISP网络拓扑多点测量及其特征分析实例[J]．软件学报，2005,16(5):846-856

[4] COATES M,HERO A III,NOWAK R,YU B.Internet tomography[J].IEEE Signal Process Magazine,2002,19(3):47-65.

[5] 赵洪华，陈鸣．基于网络层析成像技术的拓扑推断[J]．软件学报，2010,21(1):133-146

[6] DUFFIELD N,PRESTI F.Network tomography from measured end-to-end delay covariance[J].IEEE/ACM Transactions on Networking,2004,12(6):978-992.

[7] 李勇军，蔡皖东，王伟．基于端到端报文丢失的网络拓扑推测算法研究[J]．通信学报，2007,28(10):85-91

[8] SHIH M F,HERO A.Hierarchical inference of unicast network topologies based on end to end measurements[J].IEEE Transactions on Signal Processing,2007,55(5):1708-1718.

[9] CASTRO R,COATES M.,NOWAK R.Likelihood based hierarchical clustering[J].IEEE Transactons on Signal Processing,2004,52(8):2308-2321.

[10] NI J,XIE H,TATIKONDA S.Efficient and dynamic routing topology inference from end-to-end measurements[J].IEEE/ACM Transactions on Networking,2010,18(1):123-135.

[11] ERIKSSON B,DASARATHY G,BARFORD P.Efficient network tomography for internet topology discovery[J].IEEE/ACM Transactions on Networking,2012,20(3):931-943.

[12] FEI G,HU G.Improving maximum-likelihood-based topology inference by sequentially inserting leaf nodes[J].IET Communications,2011,5(15):2221-2230.

[13] 费高雷．基于单播端到端测量的网络性能参数估计方法研究[D]．成都：电子科技大学博士学位论文，2012

[14] 杨京礼，姜守达，魏长安，孙超．一种高效的单播网络自适应拓扑推测算法[J]．电子学报，2013,41(10):1888-1894

[15] HENRY S,JOHN W W.Probability,Statistics,and random processes for engineers(fourth edtion)[M].New Jersey:Pearson Education Inc,2011.

[16] 现代数学手册．随机数学卷[M]．武汉：华中科技大学出版社，2000

[17] 周勇，马昀蓓，谢尚宇，王晓靖．理工科概率统计（原书第8版）[M]．北京：机械工业出版社，2009

[18] 饶云华，曹阳，杨艳，吴锐．基于Pareto分布的IP骨干节点输入通信量模型[J]．计算机科学，2006,33(3):27-28

10.3969/J.ISSN.1672-7274.2016.05.011

TN911 文献标示码：A

1672-7274（2016）05-0036-04