基于多矿物模型分析的孔隙度计算方法在M地区中的应用

李 权,张占松,2*,袁少阳,黄 成,魏 旸

(1.长江大学 地球物理与石油资源学院，湖北 武汉 430100;2.长江大学 油气资源与勘探技术



基于多矿物模型分析的孔隙度计算方法在M地区中的应用

李 权1,张占松1,2*,袁少阳1,黄 成1,魏 旸1

(1.长江大学 地球物理与石油资源学院，湖北 武汉 430100;2.长江大学 油气资源与勘探技术

教育部重点实验室，湖北 武汉 430100)

针对复杂岩性储层，选用多矿物模型分析的方法进行测井解释。综合分析研究区岩心资料，选择合适的岩石矿物组分和测井曲线，建立测井响应方程组。根据最优化原理，选用MATLAB最优化函数“lsqlin”对该方程组求解，得到各矿物组分的体积百分含量，根据计算的矿物含量采用综合骨架体积模型，计算储层孔隙度。实际测井资料应用表明，该方法能够有效地评价复杂岩性储层孔隙度，其中密度的综合骨架模型更适合研究区的评价，与常规测井解释方法对比,该方法效果显著，能够提供更多的关于地层矿物组分的信息。

多矿物模型；复杂岩性；线性方程组；孔隙度

0 引言

孔隙度计算的主要思路是从储层测井曲线特征出发，利用测井资料进行综合分析。计算储层孔隙度的方法有多种[1,2]，主要有体积模型法、基于岩心分析资料的单因素(声波时差、密度、中子)拟合法等。基于岩心分析资料的单因素拟合法，在岩性较为单一的储层应用效果较好。对于岩性复杂的储层，常规方法存在明显缺陷，计算精度达不到储层定量评价标准。主要原因是组成岩石的矿物组分多样，每一种矿物组分的骨架响应值不同，导致岩石的综合骨架值无法确定。近年来，随着数学的进步，推动了测井参数计算方法的进步，发展了以神经网络，模糊识别等模式识别技术为基础的孔隙度评价方法[3-5]。多矿物模型分析的最优化测井解释方法，能够综合利用多条测井曲线，提供更多的地层岩石和孔隙流体信息，从而有效地评价复杂岩性地层[6,7]。如何综合利用所有的测井信息和更为有效地使用多种解释模型，并结合岩心分析等实验资料，研究和评价复杂油气藏，显得尤为重要[8]。

选取具有岩性复杂，储集空间多样，非均质性强等特征，位于伊拉克M地区某油田作为研究区。运用多矿物模型分析的方法，建立测井响应方程组，得到一个带约束条件的最优化问题。结合MATLAB最优化函数对该问题求解，得到岩石的矿物组分含量，进而利用综合骨架体积模型计算储层孔隙度。

1 研究区地质概况及孔隙度评价难点

1.1 地质概况

研究区位于伊拉克某油田，其地质构造格局主要是由三次大规模的造山运动所决定的[9]。该地区在复杂的构造条件下，形成了较为复杂的岩性类别和储集空间，储集空间以孔隙型为主，还有裂缝型和裂缝-孔隙型。由分析薄片资料可知，孔隙类型有粒间孔隙、粒内溶孔、铸模孔、晶间孔隙等。分析岩心物性资料和裂缝数据可知，孔隙度主要分布在4%～12%之间，渗透率主要分布在0.2～5mD之间，属于低孔低渗储层[10]。由研究区的取心和录井资料可知，岩性以碳酸盐岩为主，夹杂碎屑岩，岩性复杂多样。岩性分布比例如图1所示。

图1 研究区岩性分布比例Fig.1 Lithologic distribution proportion of research section

1.2 孔隙度评价难点

孔隙度常规计算方法主要是体积模型法和岩心刻度法。体积模型法的关键是要知道岩石骨架的测井响应值，而岩心刻度法则需要孔隙度与测井曲线之间有较高的相关性。对于前者，研究区岩性多样，导致岩石的骨架响应值不固定，因此该方法不适用；对于后者，从研究区的录井资料和取心资料中发现，孔隙度与各测井曲线之间并没有较好的相关性。图2、图3给出了岩心孔隙度与孔隙度曲线交会图。从图中可以看到，两者呈现出散乱的对应关系。因此，考虑利用多条曲线结合数学方法来提高孔隙度的计算精度。

图2 孔隙度与密度交会图Fig.2 Crossplot of porosity and DEN

图3 孔隙度与声波交会图Fig.3 Crossplot of porosity and AC

2 基于多矿物分析的孔隙度计算

2.1 多矿物模型分析原理

把岩性复杂的砂岩或碳酸盐岩地层看成是由不均匀的几个部分组成的几种骨架组分(∑Vmai)、泥质(Vcl)和孔隙流体(Φ)。地层对测井仪器的响应方程可由岩石体积物理模型表示。例如,对于含有m种骨架组分的地层,密度测井可用响应方程[11]表示为:

ρb=ρ1V1+ρ2V2+…+ρjVj+…+ρmVm+ρclVcl+ρΦVΦ

(1)

(1)式中，Vj、ρj分别为地层中第j种骨架组分的体积百分含量和密度值；Vcl、ρcl分别为泥质成分的体积百分含量和密度值；VΦ、ρΦ分别为孔隙流体的体积百分含量和密度值，即孔隙体积含量和孔隙密度。

同样，中子、声波、自然伽马测井曲线也可写成与上式相同的测井响应方程[11]。设有N-1条测井曲线，要计算M个矿物组分含量(包括孔隙体积含量和泥质含量)，并且N≥M。于是，连同平衡方程可以列出N个方程，这样就形成了线性超定方程组[5]。当N=M时，该方程组为恰定方程组。

L1=P11V1+P12V2+…+P1jVj+…+P1MVM

L2=P21V1+P22V2+…+P2jVj+…+P2MVM

…

Li=Pi1V1+Pi2V2+…+PijVj+…+PiMVM

(2)

…

1=V1+V2+…+Vj+…+VM

方程组(2)式中，Li为测井曲线读值；Pij为组分的测井响应值；Vj为组分体积含量。方程组(2)可以简化为:L=PV。

L为L1、L2…Li构成的矩阵，P为方程组的系数构成的系数矩阵，V为求解的体积含量构成的矩阵。该线性方程组需要一些必要的约束条件，以保证多矿物分析的结果是合理和符合地质规律的[4]。设置每种矿物的体积含量值均在0～1。由于存在测量误差以及模型的建立不精确等因素，因此不可能获得上述方程组的真实解[8]。考虑到这一点，分别让测井曲线和测井响应值乘上相应的权系数，再代入方程组进行计算，则方程组变为：LW=PW·V。

W为权系数矩阵，它是一个对角矩阵，属于未知量，是由各条测井曲线的误差所决定的。在实际应用中，需要根据地区情况，适当调整权系数矩阵中的元素。调整的原则是通过调节W中的元素，使得孔隙度的计算结果更加符合岩心分析结果。

2.2 曲线选取与多模型构造

地层矿物反映在交会图上，首先需要确定能有效反映岩石骨架性质的曲线或参数[7]。如图4、图5所示，中子、密度曲线均对岩石矿物组分有一定的区分度。同时考虑到研究区只有常规测井资料以及线性方程组不能含有非线性曲线(电阻率曲线，PEF等)的限制，因此，选择了自然伽马和三孔隙度曲线(密度、中子、声波)作为多矿物分析的曲线。由图1的岩性分布比例以及曲线的交会图可以看出该区主要矿物组分有灰岩、白云岩、砂岩、硬石膏、泥质以及孔隙流体。

图4 中子与密度交会图Fig.4 Crossplot of NPHI and DEN

图5 声波与自然伽马交会图Fig.5 Crossplot of AC and GR

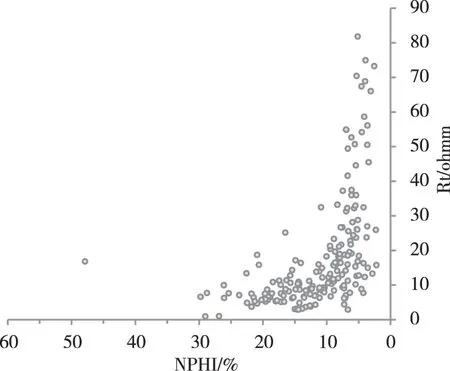
随着新测井方法的出现，如岩性密度，自然伽马能谱等，使得单一模型可确定的组分个数也随之增加。在大多数情况下，地层中组分数超过了单一模型求解的能力(N

(3)

(3)式中，Ei是第i个单一模型的相对误差；D(j)为该深度点第j条测井曲线的值；n、m分别为曲线数和组分种类数；Vti(k)为该模型的第k个组分的百分含量(由线性方程组求解得到)；Pi(j,k)为该模型中第k个组分的第j个测井响应值。在实际应用中，构造了3个单一模型：灰岩、白云岩、砂岩、泥质和孔隙流体；灰岩、白云岩、硬石膏、泥质和孔隙流体；灰岩、砂岩、泥质和孔隙流体。对于各种矿物组分的测井响应值，可以用2种方法确定。一是根据岩心分析的孔隙度和各种组分的测井曲线值之间的相互关系建立交会图，再根据交会图上点子的分布确定出当孔隙度趋于0时对应的测井值，即为骨架的测井响应值；另一种方法是应用测井曲线确定骨架值。例如确定骨架中子值，应用中子和电阻率曲线做交会图。当电阻率趋于无穷大时，对应的中子值就为该骨架的中子响应值[12]。如图6、图7，则是运用该方法确定灰岩的骨架中子值为1(%)，骨架声波时差值为50(us/ft)。

图6 声波时差与电阻率交会图Fig.6 Crossplot of AC and RT

图7 中子与电阻率交会图Fig.7 Crossplot of NPHI and RT

2.3 利用MATLAB解方程组

在求解各组分的体积含量时，需要求解由测井响应方程所构造的线性方程组，并且该方程组是带有约束条件的。求解每个单一模型所构造的计算矿物组分含量的测井响应方程组，其实质就是一个求解带有约束条件的超定方程组的数学问题。而使用MATLAB中的最优化算法，便可以解决上述问题。

在实际应用中选择MATLAB的最优化函数lsqlin来求解线性方程组。优化函数lsqlin的具体形式[13,14]如下：

X=lsqlin(A,B,[],[],AEQ,BEQ,LB,UB)

(4)

(4)式中，A和B代表线性方程组AX=B的系数矩阵和常数项向量，X 为未知项向量；参数AEQ与BEQ则构成线性约束条件，即AEQ·X=BEQ；LB与UB则代表解的上界和下界。该函数的用处是求解超定或恰定线性方程组，并且函数还可以将测井响应方程组的约束条件考虑进去，从而得到满足约束条件的最优解。

2.4 孔隙度计算

通过前面的方程组求解可以得到岩石的矿物组分含量，此时便可以运用综合骨架体积模型来计算储层孔隙度。以密度的综合骨架体积模型为例，由

DEN=D1V1+D2V2+…+DiVi+DfΦ和DEN=DmaVma+DshVsh+DfΦ可得如下的孔隙度计算公式：

(5)

(5)式中为Dma骨架密度，Vma为骨架体积含量；m为除泥质和孔隙流体以外的矿物组分种类数；Vi和Vsh分别为矿物组分含量和泥质含量；Di为各种矿物组分的密度响应值，Dsh为泥质的密度响应值，Df为孔隙流体密度，这里为1g/cm3；DEN为密度曲线值。

同样也可以得到中子和声波的综合骨架体积模型的计算公式，来计算储层孔隙度。对比这3种方法的计算结果，选择效果最好的方法。

3 孔隙度方法对比

为了比较不同孔隙度计算方法的效果，选择几种常规方法与基于多矿物模型分析的孔隙度计算方法对比。常规计算方法有一元线性回归法、多元线性回归法和逐步回归法等[15]。

1)一元线性回归孔隙度解释模型

Φ=0.406 9×AC-14.398

Φ=-23.272×RHOB+70.062

Φ=0.579 3×NPHI+2.921 1

2)多元线性回归孔隙度解释模型

Φ=0.283 7×AC+6.155 5×RHOB+0.324 4×NPHI-27.210 8

3)逐步回归孔隙度解释模型

Φ=0.293×NPHI+0.215×AC-6.752

Φ=0.943×NPHI-0.019×NPHI2+0.196×AC-9.895

4)基于多矿物模型分析的孔隙度解释模型

在应用基于多矿物模型分析的孔隙度解释模型中，合理地构造多个单一模型和调整权系数矩阵W，是提高解释精度的关键。利用MATLAB编程实现该算法，对研究井段进行了处理，并与其它孔隙度计算方法进行对比。如图8所示，为某研究井段的处理结果对比图，图中的矿物组分剖面则是通过各组分百分含量曲线进行填充而得到，EGR、ERHOB、ECNL等(第2～5道)则是自然伽马和孔隙度曲线的重构曲线，第6～8道分别是密度、声波和中子的综合骨架体积模型计算的储层孔隙度(基于多矿物模型分析的孔隙度解释模型)，第9～11道分别是常规方法中的逐步回归法、多元线性回归法和一元线性回归法计算的孔隙度。

结果显示：由矿物组分含量构造的重构曲线与原测井曲线大致吻合；在对比常规计算方法的效果中，基于多矿物模型分析的孔隙度计算方法效果更好，其中密度的综合骨架体积模型计算的结果更符合实际地层情况；矿物组分剖面(第12道)与录井剖面(第13道)对比，矿物组分分析的结果也有一定的准确性。由此可以说明多矿物模型分析的方法能够有效地提高复杂岩性储层孔隙度的计算精度，同时也能提供更多的地层矿物组分信息。

4 结论与讨论

4.1 结论

针对研究区复杂岩性特点，选取多矿物模型方法进行分析。通过多模型构造和最优化等问题的解决，形成了一套基于多矿物模型分析的孔隙度计算方法。运用该方法对研究区井段进行了处理，得到如下结论：

1)对于复杂岩性储层的测井评价，基于多矿物模型分析的孔隙度计算模型，能够有效地提高储层孔隙度的计算精度，其效果优于常规测井解释方法，同时也能提供更多的关于地层矿物组分的信息。

2)针对多矿物模型分析中的最优化问题，lsqlin函数可以较准确地求解各矿物组分的含量，从而为确定岩石的综合骨架响应值提供依据。

4.2 讨论

1)对于多矿物模型分析中的最优化问题，可以尝试选取其它的最优化方法来解决，例如共轭梯度法、遗传算法等。通过比较这些方法计算的结果，选择其中效果较好的方法。在方法的选择方面，也需要考虑各种方法的计算时间。因为对于实际资料这一庞大的数据，往往需要比较长的处理时间。

图8 孔隙度计算方法对比图Fig.8 Comparison of calculation methods of porosity

2)在利用多矿物模型分析方法时，建议多测量，多增加一些对岩性矿物比较敏感的测井曲线，例如地层元素测井曲线。这样可以综合利用更多的测井信息来预测矿物组分含量，从而更准确地计算储层孔隙度参数。

[1] 刘开元,贺振华,许艳秋.碳酸盐岩储层孔隙度预测方法研究及其在南海某区的应用[J].石油物探，2014,53(2):232-237.

[2] 张兆辉,高楚桥,刘娟娟.基于地层组分分析的储层孔隙度计算方法研究[J].岩性油气藏,2012,24(1):97-100.

[3] 雍世和,张超谟.测井数据处理与综合解释[M].东营:中国石油大学出版社,2002:533-564.

[4] 汪忠德.BP人工神经网络法(ANNS)在塔中地区碳酸盐岩测井评价中的应用[J].石油天然气学报(江汉石油学院学报),2008,30(2):253-255.

[5] 侯俊胜.神经网络方法在煤层气测井资料解释中的应用[J].地质与勘探,1999,35(3):41-45.

[6] 张建龙.多矿物模型分析在潜山地层测井中的应用[J].测井技术,2000,24(3):227-230.

[7] 吴建,胡向阳,何胜林.多矿物模型在复杂岩性地层中的应用[J].科学技术与工程,2013,13(30):9018-9024.

[8] 周改英,赵喜亮.多矿物模型分析的最优化测井解释[J].河南石油,2005,19(5):21-22.

[9] 韩耀祖,陈伟,欧成华,等.伊拉克米桑地区阿布古拉卜背斜的几何解析和运动学模拟[J].新疆石油地质，2014，2,35(1):124-129.

[10]朱筱敏.沉积岩石学(第四版)[M].北京:石油工业出版社，2008:40-52.

[11]雍世和.最优化测井解释[M].东营:石油大学出版社,1995:54-62.

[12]李宁,陶宏根,刘传平.酸性火成岩测井解释理论、方法与应用[M].北京:石油工业出版社,2009:49-50.

[13]周建兴,岂兴明,矫津毅,等.MATLAB从入门到精通[M].北京:人民邮电出版社,2008:209-214.

[14]陈杰.MATLAB宝典[M].北京:电子工业出版社,2013:172-191.

[15]陈文浩,王志章,董少群,等.核岭回归方法解释致密砂岩储层孔隙度[J].测井技术,2015,12(6):710-714.

Application of calculation method of porosity based on multi-minerals analysis in M area

LI Quan1, ZHANG Zhansong1,2*, YUAN Shaoyang1,HUANG Chen1,WEI Yang1

(1.Geophysics and Oil Resource Institute, Yangtze University, Wuhan, Hubei 430100,China;2.Key Laboratory of Exploration Technologies for Oil and Gas Resources, Ministry of Education，Yangtze University，Wuhan, Hubei 430100,China)

For the complex lithology reservoir, the method of multi-minerals analysis is selected and used for logging interpretation. An analysis of core date which is collected in the research section is done first. Then the appropriate mineral and logging curves are chosen to build multi-minerals model equations. According to the principle of optimization, the MATLAB optimal function “lsqlin” is used to solve the linear equations. The result is the relative volume of every mineral composition, which could be used to compute the relative volume and logging response value of the rock matrix. And then the method of volume model is used to compute the reservoir porosity. The practical application shows that this method can calculate the porosity of complex lithology formation effectively, of which the volume model of density is more applicable to the research section. Compared to the conventional logging interpretation method, its effect is remarkable, and it can provide more information about mineral composition of the formation.

multi-minerals model; complex lithology; linear equations；porosity

1004—5570(2016)05-0077-06

2016-03-08

国家科技重大专项(2011ZX05030-004)

李 权(1991-)，男，硕士研究生，研究方向：测井资料综合解释,E-mail:530668267@qq.com.

*通讯作者：张占松(1965-)，男，博士，教授，研究方向：地球物理与石油资源,E-mail:zhangzhs@yangtzeu.edu.cn.

TE122

A