求解非线性抛物组的新算法——双插值有限元

陈传淼，胡宏伶

(湖南师范大学数学与计算机学院，中国 长沙 410081)



求解非线性抛物组的新算法
——双插值有限元

陈传淼*，胡宏伶

(湖南师范大学数学与计算机学院，中国 长沙 410081)

本文提出了双插值有限元法求解一类非线性抛物组，它对未知函数和系数都采用了插值，于是某些常数矩阵可一次性计算好，每时间层组装刚度矩阵很简单.它是一种经济格式.

非线性抛物组；有限元；双插值；经济格式

随着科学技术的发展，非线性抛物问题出现在许多实验领域，如高温传输、核聚变、半导体、超导、石油开发、金融和图像识别等.本文特别关注核聚变中的三温计算问题.

在经典有限元法或有限体积法中，虽然有多种格式离散非线性抛物问题.但数值求解的主要困难是计算工作量极其巨大.

1)每个时间层的离散工作量巨大.

2)牛顿法求解非线性方程组需3～4次线性化(计算切矩阵).

3)必须计算数千数万时间层.

三种困难交织在一起成为大规模求解的主要困难之一，因此发展高效算法有重要意义.

对一类具有散度型结构的非线性方程

ut-(a(u)u)+b(u)=f,u=0,x∈Γ,u(x,0)=ψ,x∈Ω.

(1)

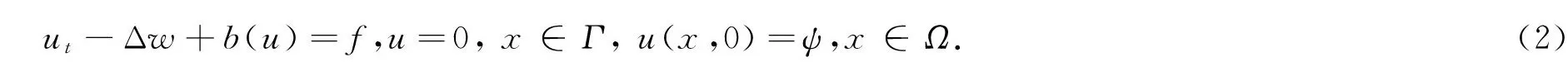
直接插值u,w,b(u),称为插值系统有限元(ICFEM)，它在每个时间层上的离散方程组可以一次性计算好，与tn无关，因此可节省离散时间，是一种经济格式.Zlamal[1]在假设|uh|≤C时证明了最佳阶O(h2);不要此假设，陈传淼-Larsson-Zhang[2](1989)在分块均匀网格三角形线元用超收敛技巧，首次证明几乎最佳收敛性O(h2ln h).以后最佳收敛性及二次元的超收敛性也被研究.但是Kirchhoff变换只适合单个方程，对抛物组无效.

为求解非线性抛物组，我们提出双插值有限元，即同时插值函数u及系数a(u),b(u),可一次性计算某些常数矩阵，每时间层组装刚度矩阵很简单.它是一种经济格式.

1 双插值有限元法(BIFE)

插值系数法的基本思想是：插值的函数与函数的插值在最佳阶误差意义不是等效的.

在d维单元σ上m个点xp,适当光滑函数u(x)及复合函数a(u)的l次插值分别为

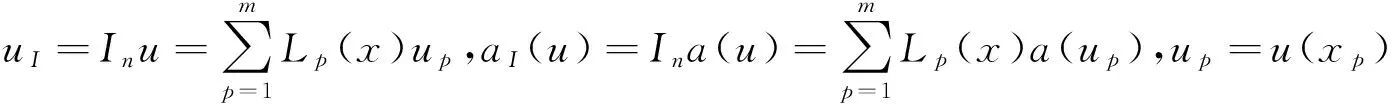
容易证明最佳阶误差估计

‖Ina(u)-a(Inu)‖k,p,r≤C(u)hl+1-k,k=0,1.

(3)

因为‖u-Inu‖及‖a(u)-Ina(u)‖有这种估计.

我们讨论拟线性抛物问题(也可以是方程组)

c(u)ut-Dj(a(u)Dju)+b(u)=f(t,x),w(0,x)=w0(x),w=0,x∈Γ.

(4)

其中系数a(u),c(u)为正定,b(u)为u光滑函数.

我们的新思想在于：取u为未知函数，同时引进a(u),b(u),c(u)作为相关的变量(虽然它们不是独立变量).在每个单元σ直接作分片线性插值ui,aI(u),bI(u),cI(u).

为简单起见，讨论后向Euler-双插值有限元Un∈Sh满足

(5)

这里，v=Li,i=1,2,…,N,

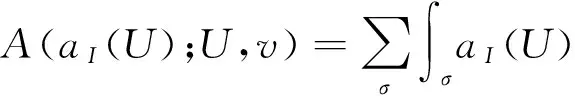
是a,u,v的三线性型.

可以计算单元积分

Jσ(Li)=∫σ{aI(U)ULi+bI(U)Li}dx=

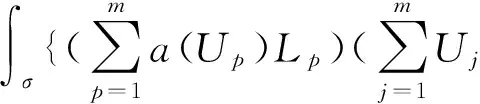
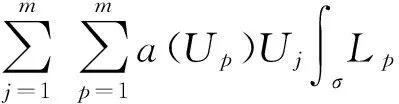
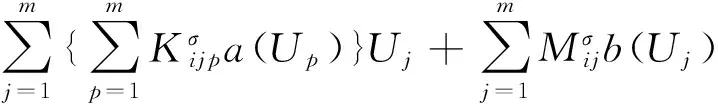
(6)

这里单元刚度矩阵系数和质量矩阵系数

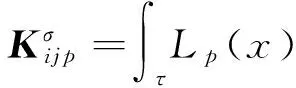
关于i,j是对称的，可以一次性计算好.于是单元测度矩阵可用简单的乘法得到

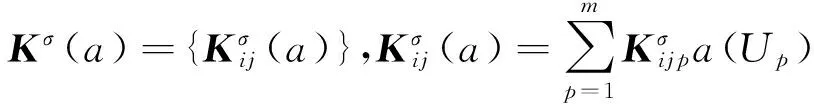
类似地有单元质量矩阵Mσ(c),Mσ(b).对已给U，显然Kσ(a),Mσ(c),Mσ(b)是对称的.

组集所有单元积分并处理本质边界条件，得到总体非线性方程组

Q(Un+1)≡M(cn)(Un-Un-1)+kK(an)Un+kM(bn)-kMFn=0.

(7)

这里M(cn),K(an)为对称正定阵.由此看到，双插值有限元法有以下3个优点:

1)像ICFEM一样，矩阵Kijp,Mij可一次性算好，组装Kij(U),Mij(U)很简单；

2)对多未知变量方程组适用，只要系数a(u),b(u),c(u)与t,x无关即可.特别地，核聚变中的三温方程正好可以变换为这种散度形式.

3)如何高效求解非线性方程组(7),是另一个重要问题[5]，将在其他论文讨论.

[1] ZLAMAL M.A finite element method of the nonlinear heat equation[J].RAIRO Model Anal Numer,1980,(14):203-216.

[2] CHEN C M,LARSSON S,ZHANG N Y.Error estimates of optimal order for finite element methods with interpolated coefficients for the nonlinear heat equation[J].IMA J Numer Anal,1989,(9):507-524.

[3] 陈传淼，黄云清.有限元高精度理论[M].长沙：湖南科技出版社,1995.

[4] 陈传淼.有限元超收敛构造理论[M].长沙：湖南科技出版社,2001.

[5] HU H L,CHEN C M,PAN K J.Time extrapolation algorithm for parabolic problems[J].J Comput Math,2014,32(2):183-194.

(编辑 HWJ)

The Bi-Interpolation Finite Element Method —A New Algorithm for Solving Nonlinear Parabolic Systems

CHENChuan-miao*,HUHong-ling

(College of Mathematics and Computer Science,Hunan Normal University,Changsha 410081,China)

The bi-interpolation finite element method for solving nonlinear parabolic systems is proposed,in which both unknowns and their coefficients are interpolated,so some constant matrixes can be computed in one time,whereas at each time level the assembly stiffness matrixes are very simple.This is an economic scheme.

nonlinear parabolic systems; finte element method; bi-interpolation; economic scheme

10.7612/j.issn.1000-2537.2016.05.014

2016-06-30

国家自然科学基金资助项目(11301176,10771063)；湖南省自然科学基金资助项目(14JJ3070)

*通讯作者,E-mail：cmchen@hunnu.edu.cn

O241.82

A

1000-2537(2016)05-0081-02