转轴阶梯处椭圆裂纹应力强度因子的计算分析

何家胜 崔璨 杨帆 吴乔莉

（1.武汉工程大学机电工程学院2.中石化武汉分公司)

转轴阶梯处椭圆裂纹应力强度因子的计算分析

何家胜1*崔璨1杨帆2吴乔莉2

（1.武汉工程大学机电工程学院2.中石化武汉分公司)

转轴在运行过程中，常在阶梯处发生断裂失效。为了研究转轴阶梯处过渡圆角大小对该处裂纹扩展的影响，利用有限元方法在裂纹前沿设置奇异单元，建立了转轴的有限元分析模型。通过分析计算，得到了弯扭载荷作用下转轴阶梯处的椭圆裂纹应力强度因子的变化规律。

转轴 应力强度因子 椭圆裂纹 过渡圆角曲率 奇异单元

0 前言

转轴是组成机器的重要零件之一，其主要功能是支承作回转运动的传动零件。转轴在工作时既受弯矩作用又受扭矩作用，轴阶梯处容易发生脆性断裂失效，导致整台设备无法正常工作，给企业带来重大的经济损失，甚至造成安全事故。因此对于转轴类结构的断裂原因进行研究有着重要意义。应力强度因子是研究裂纹问题的重要断裂力学参量，在机械零部件的安全评定中有着重要的作用。在转轴的加工生产中，转轴阶梯处所取圆角的大小不同，对于转轴阶梯处的裂纹扩展会产生不同的影响。转轴阶梯处裂纹的研究属于三维裂纹问题。相对于二维裂纹而言，三维裂纹应力强度因子的研究更加困难，目前能查到的关于转轴阶梯处裂纹问题的研究文献很少。

本文采用有限元方法研究裂纹尖端处应力强度因子，借助于有限元软件ANSYS进行模拟计算。为了模拟裂纹前沿应力的奇异性，利用1/4节点位移外推法[1]沿着裂纹前沿设置了一系列三维奇异单元进行应力强度因子计算。很多有限元模拟为了简化建模[2-4]，将转轴阶梯处简化为直角或者没有阶梯，这样在阶梯处容易产生高度的应力集中，这不利于有限元的计算，更不符合实际情况。在有限元软件中，并没有弧形单元，这就在很大程度上限制了有限元法对于模拟圆角处单元的应用。本文针对以上难点，对同一转轴不同圆角下裂纹的应力强度因子进行了计算。

1 断裂力学有限元模型

本文研究的阶梯轴如图1所示。转轴有限元分析模型是由内而外建立起来的。在裂纹附近的局部小区域，裂纹奇异单元为退化的solid95单元；其余非裂纹区单元为solid45单元。

图1 阶梯轴

1.1 模型的建立

裂纹前沿的建立：先在裂纹边缘处建立一系列裂纹顶点，围绕裂纹顶点建立一系列二次奇异单元，即裂纹前沿单元，如图2所示。

图2 裂纹前沿单元

轴的建立：在建立了裂纹前沿的基础上，建立围绕裂纹的轴上其他节点，由节点组成单元，最后由单元组成整个轴模型。

圆角的建立：将圆角沿圆弧划分成多段直线，建立圆弧上各点并连接拟合出圆弧。根据计算出的圆角上节点的分布公式，在命令流中进行编辑，再用命令连接相应的各个节点组成单元，从而形成多个梯形单元，最终组成过渡圆角模型，如图3所示。

图3 过渡圆角单元

1.2 载荷及边界条件的施加

整个轴模型及其在ANSYS中的加载情况如图4所示。大径轴半径R1=42 mm，长L1=153 mm；小径轴半径R2=40 mm，长L2=192 mm；椭圆裂纹位于阶梯边处小径轴上。大径轴末端面约束了x，y，z三个方向位移。在小径轴顶端面施加扭矩，取力N1=N2=15 kN，力的方向与圆周相切；在中心处施加弯矩，取力W=30 kN，力的方向垂直向下。

图4 阶梯轴加载情况

2 直角阶梯与圆角阶梯对应力强度因子的影响

转轴阶梯处萌生裂纹时，带裂纹的直角阶梯和圆角阶梯有限元单元模型如图5（a）和（b）所示。取裂纹椭圆率为a/b=0.3，深度为3.2 mm，直角阶梯和圆角阶梯处的裂纹前沿处各点应力强度因子分别如表1和表2所示，其中θ为椭圆裂纹前沿上节点在xoy平面内与y轴的夹角，如图6所示。由表1、表2可绘制应力强度因子变化曲线，如图7所示。

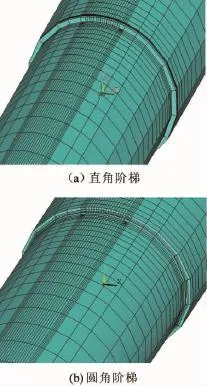
图5 带裂纹的直角阶梯和圆角阶梯有限元图

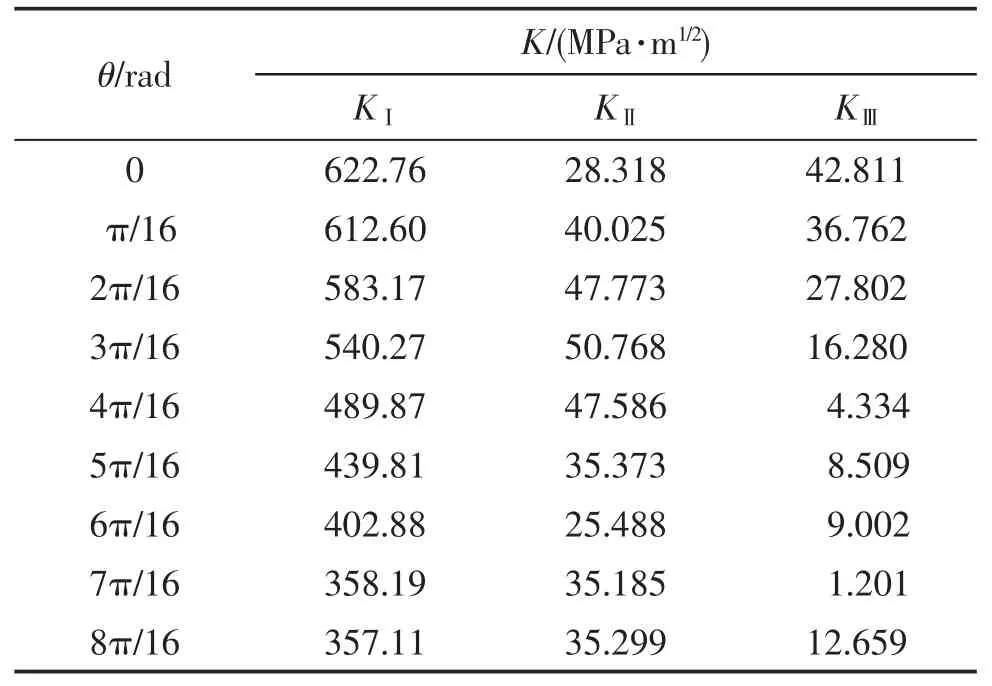
表1 直角阶梯处裂纹应力强度因子

表2 圆角阶梯处裂纹应力强度因子

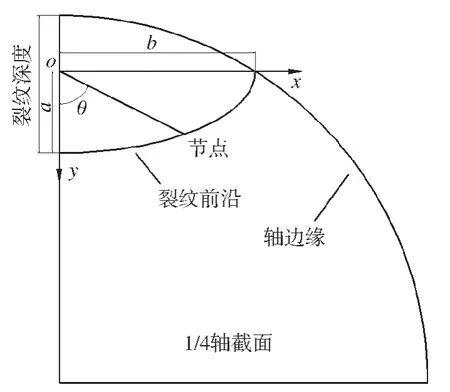
图6 裂纹前沿节点位置

图7 圆角和直角应力强度因子变化图

由表1、表2和图7(a)、(b)、(c)中曲线可知，对于KⅠ，在（5π/16，8π/16）范围内，直角阶梯处的裂纹应力强度因子KⅠ明显比圆角阶梯处裂纹应力强度因子大，且越靠近轴圆周外围的裂纹节点，直角阶梯对于该处应力强度因子的影响越大；而在（0，5π/16）范围内，两者应力强度因子KⅠ相差不大，即裂纹越深处的应力强度因子，两者对其影响越不明显。对于KⅡ，在（2π/16，8π/16）范围内差别较大，而在（0π/16，2π/16）范围内，两者相差不大。同样，对于KⅢ，在（4π/16，8π/16）范围内差别较大，而在（0，4π/16）范围内，两者相差不大。总之，圆角可有效减小裂纹尖端应力强度因子。

3 不同圆角曲率半径分别对不同深度裂纹应力强度因子的影响

查国标GB/T 6403.4—1986可知，直径为80～120 mm的零件，圆角一般取2.5 mm。为了方便分析，设椭圆长半轴b固定，取椭圆率a/b=0.3，a/b= 0.5，a/b=0.8三种不同深度裂纹作为研究对象，同样地取r1=1.5 mm，r2=2.0 mm，r3=2.5 mm三种不同曲率半径，一共9种情况，如图8、图9、图10所示。通过有限元计算，得到应力强度因子沿裂纹前沿的变化。每条不同曲线标号分别对应不同圆角曲率半径。

由图8可以看出：当椭圆率a/b增大即深度越深时，轴边缘处裂纹应力强度因子KⅠ越大，而且随着深度的增大，越靠近轴边缘处应力强度因子变化越明显；对于同一深度的裂纹，圆角越大则应力强度因子曲线越低，即相对应节点处应力强度因子越小，而且随着深度的增加，圆角曲率对于应力强度因子的影响越明显。

由图9可看出，在弯扭组合载荷作用下，KⅡ的变化曲线最小值出现在0和6π/16处，而最大值在4π/16附近；椭圆率越大，最大值越靠近中间部位，最小值越出现在最深处。当椭圆率较小时，可以明显地看到，圆角越大，应力强度因子KⅡ越小，随着椭圆率的增大，KⅡ的峰值处应力强度因子变化越平缓。因此对于KⅡ而言，椭圆率在0.5附近时，KⅡ随着圆角曲率的变化不明显，且峰值最小。

由图10可看出，裂纹应力强度因子KⅢ和KⅠ的变化规律接近，峰值均出现在裂纹最深点。但越接近轴边缘处，应力强度因子KⅢ变化越剧烈，均在（4π/16，8π/16）范围内出现第二个峰值，且椭圆率越大，该峰值越陡。但对于整个KⅢ变化曲线来说，圆角曲率的增大可有效减小轴边缘处的应力强度因子。

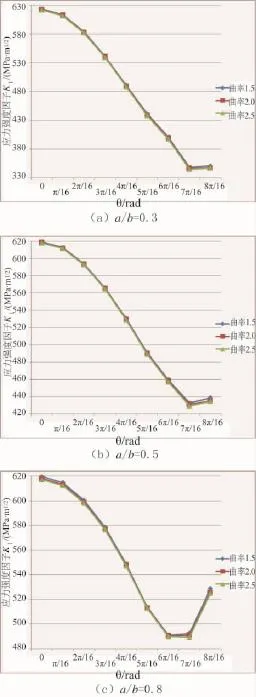
图8 应力强度因子KⅠ变化图

4 结语

（1）通过逐点建模法，建立了含三维曲面椭圆裂纹的转轴有限元模型，分析并比较了直角阶梯和圆角阶梯处裂纹应力强度因子的不同，得出圆角可有效减小裂纹尖端应力强度因子的结论。

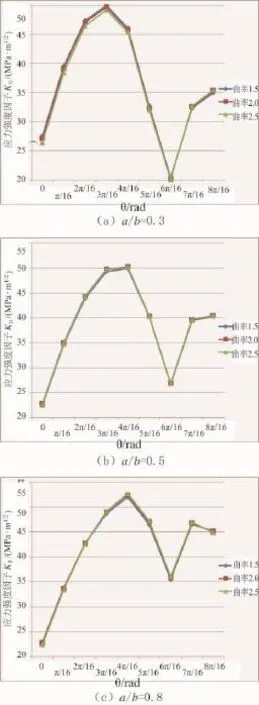
图9 应力强度因子KⅡ变化图

（2）通过有限元法计算出不同圆角曲率的裂纹前沿处应力强度因子的KⅠ、KⅡ和KⅢ的数值解，将它们进行对比并作出其随角度θ的变化曲线。由这些曲线图可直观地看出其峰值所在位置，在不同的深度，圆角曲率对于不同类型裂纹应力强度因子的影响也不同。总之，圆角曲率的增大可有效减小裂纹前沿处的应力强度因子。

（3）本文的计算方法可以用来模拟圆角阶梯处含裂纹的轴类零部件，并求出其应力强度因子KI、KⅡ和KⅢ，所得计算结果可在各类轴的安全评定中作为参考。

图10 应力强度因子KⅢ变化图

[1]陈银强.圆柱体表面椭圆裂纹应力强度因子的有限元分析和研究[D].武汉：武汉工程大学，2006.

[2]彭红星.传动轴的有限元分析与设计优化[J].机械工程师，2009（12）：114-115.

[3]唐良兵，王伟.基于ANSYS的汽车传动轴的有限元分析[J].机械，2013（1）：45-48.

[4]钟佩思，王景林，刘梅，等.基于有限元的传动轴受扭分析[J].机械传动，2008（5）：88-90.

Calculation Analysis of Stress Intensity Factor of Elliptical Crack at the Ladder of Shaft

He JiashengCui CanYang FanWu Qiaoli

The fracture failure of the shaft always occurs at the ladder during the operation.In order to study the effect of the transition fillet at the ladder of the shaft on the crack propagation,the finite element method is applied to set the singular element at the crack front and the finite element analysis model of the shaft is built. Based on the analysis and computation,the variation regularity of the stress intensity factor of the elliptical crack at the ladder of shaft under the torsional loading is obtained.

Shaft；Stress intensity factor；Elliptical crack；Curvature of the transitional fillet；Singular element

TQ 050.2

10.16759/j.cnki.issn.1007-7251.2016.08.002

2015-11-22）

*何家胜，男，1958年生，教授。武汉市，430200。