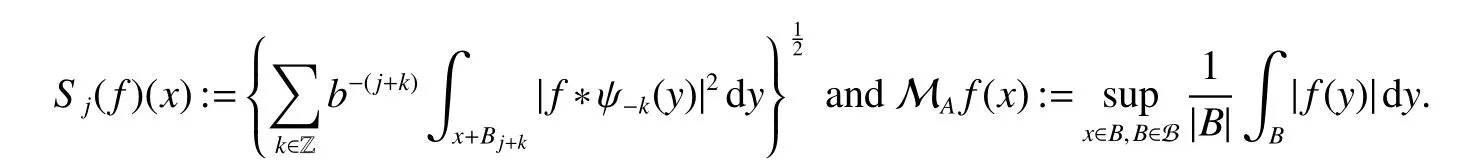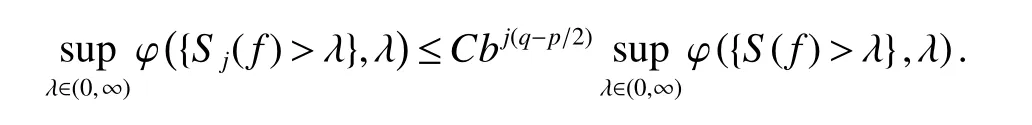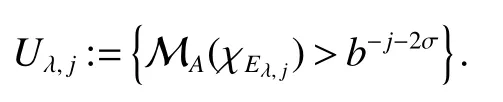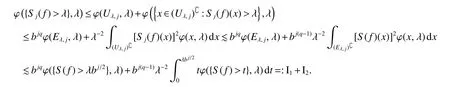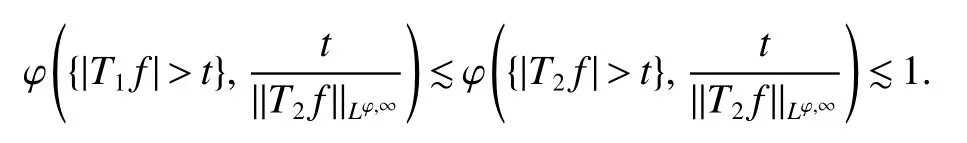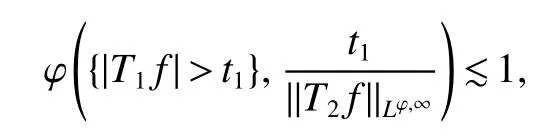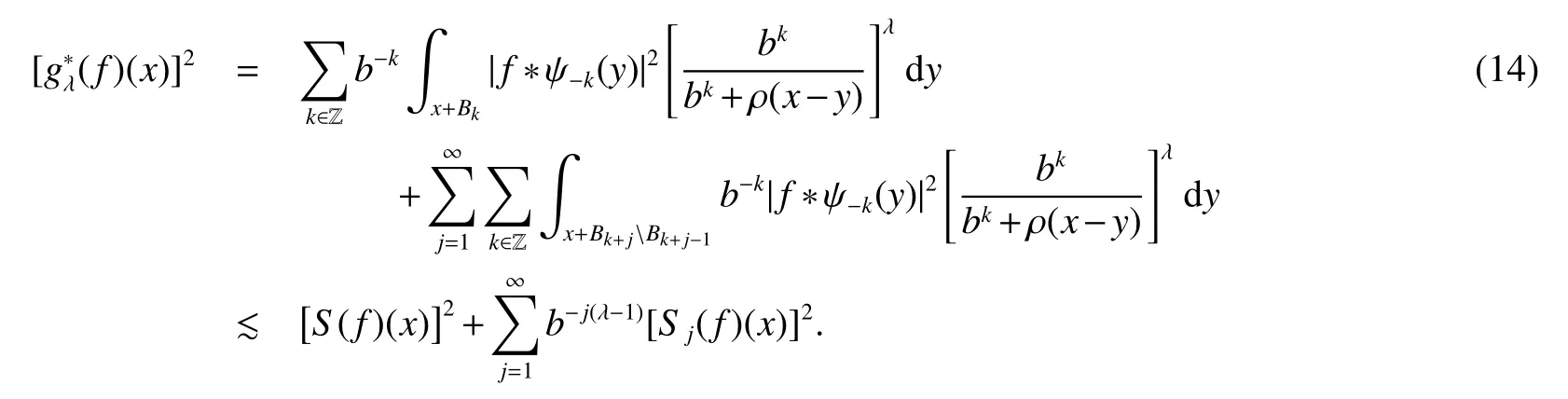Boundedness of Littlewood-Paley Functions on Anisotropic Weak Hardy Spaces of Musielak-Orlicz Type∗

QI Chunyan,ZHANG Hui,LI Baode

(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)

Abstract: Let A be an expansive dilation and ϕ:Rn×[0,∞)→[0,∞)an anisotropic p-growth function with p∈(0,1].Let (Rn)be the anisotropic weak Hardy space of Musielak-Orlicz type defnied via the grand maximal function.In this article,by using the atomic decomposition of (Rn),the authors obtain the boundedness of the anisotropic Littlewood-Paley Lusin-area function,the anisotropic g-function and the anisotropic -function from (Rn)to weak Musielak-Orlicz-type space.Moreover,the range of λ in the boundedness of the anisotropic -function associated to(Rn)coincides with the known best conclusions in the case when(Rn)is replaced by the classical Hardy space or its weighted variant,the Musielak-Orlicz Hardy space or the anisotropic Musielak-Orlicz Hardy space,respectively.

Key words:anisotropic;expansive dilation;Muckenhoupt weight;Musielak-Orlicz function;weak Hardy space;Littlewood-Paley function;atom

0 Introduction

Let Aq(Rn)withq∈ [1,∞]denote the class ofMuckenhoupt weightsand φ be agrowth function(see[1])which means that φ :Rn× [0,∞)→ [0,∞)is a Musielak-Orlicz function such that φ(x,·)is an Orlicz function and φ(·,t)is a Muckenhoupt A∞(Rn)weight.It is known that Musielak-Orlicz functions are the natural generalization of Orlicz functions that may vary in the spatial variables(see,for example,[1,2]).Recently,Ky[1]introduced a newMusielak-Orlicz HardyspaceHφ(Rn),via the grand maximal function.It is worth noticing that some special Musielak-OrliczHardy spaces appear naturally in the study of the products of functions inBMO(Rn)andH1(Rn)(see[3–5]),the endpoint estimates for the div-curl lemma and the commutators of singular integral operators(see[3,5]).

Let ϕ :Rn×[0,∞)→ [0,∞)be an anisotropic growth function(see[6,Defniition 3]).Recently,in order to fnid a appropriate general space including weak Hardy space of Fefferman and Soria[7],weighted weak Hardy space of Quek and Yang[8]and anisotropic weak Hardy space of Ding and Lan[9]as special cases,we introduced the anisotropic weak Hardy space of Musielak-Orlicz type(Rn)via the grand maximal function in a submitted drift,and obtained some maximal function characterizations of(Rn).

Let ϕ be an anisotropicp-growth function withp∈ (0,1],which is also a particular anisotropic growth function ϕ(see Defniition 3 below).The aim of this article is to prove the boundedness of the anisotropic Littlewood-Paley Lusinarea function,the anisotropicg-function and the anisotropic-function from(Rn)to weak Musielak-Orlicz-type space(see Theorems 1 and 2 below).Here,we point out that the atomic decomposition characterization ofand the superposition principle adapted to the weak Musielak-Orlicz-type space(see[10,Lemma 3.5]),which is an extension of Stein,Taibleson and Weiss in[11],play an important role in the proofs of the boundedness of the anisotropic Littlewood-Paley Lusin-area and the anisotropicg-function on these spaces(see Theorem 1 below).

This article is organized as follows.In Section 1,we frist recall some notations and defniitions concerning Musielak-Orlicz functions,expansive dilations,anisotropic Muckenhoupt weights andp-growth function.Then we introduce the anisotropic weak Hardy space of Musielak-Orlicz type,(Rn),via the grand maximal function,and establish the boundedness of the anisotropic Littlewood-Paley Lusin-area function,the anisotropicg-function and the anisotropic-function,the proofs of which is given in Section 2 and Section 3.

Finally,we make some conventions on notations.Let N:={1,2,...}and Z+:={0}∪N.For any α :=(α1,...,αn)∈:=(Z+)n,|α|:= α1+ ···+αnThroughout the whole paper,we denote byCapositiveconstantwhich is independent of the main parameters,but it may vary from line to line.Thesymbol DFmeans thatD≤CF.IfDFandFD,we then writeD∼F.IfEis a subset of Rn,we denote by χEitscharacteristic function.For anya∈R,adenotes themaximal integernot larger thana.If there is no special instructions,any space X on Rnis denoted simply by X.Denote by S thespace of all Schwartz functionsand Sthespace of all tempered distributions.For any setEandt∈(0,∞),let ϕ(E,t):=Eϕ(x,t)dx,and,for any measurable functionfandt∈(0,∞),let{|f|>t}:={x∈Rn:|f(x)|>t}.

1 Preliminaries and main results

First we recall the notion ofexpansive dilationson Rn;see[12,p.5].A realn×nmatrixAis called anexpansive dilation,shortly adilation,if minλ∈σ(A)|λ|>1,where σ(A)denotes the set of alleigenvaluesofA.Let λ−and λ+be twopositive numberssuch that

In the case whenAis diagonalizable over C,we can even take λ−:=min{|λ|:λ ∈ σ(A)}and λ+:=max{|λ|:λ ∈ σ(A)}.Otherwise,we need to choose them sufficiently close to these equalities according to what we need in our arguments.

It was proved in[12,p.5,Lemma 2.2]that,for a given dilationA,there exist a numberr∈(1,∞)and a set∆ :={x∈Rn:|Px|<1},wherePis some nondegeneraten×nmatrix,such that∆ ⊂r∆ ⊂A∆,and one can and do additionally assume that|∆|=1,where|∆|denotes then-dimensional Lebesgue measure of the set∆.LetBk:=Ak∆ fork∈Z.ThenBkis open,Bk⊂rBk⊂Bk+1and|Bk|=bk,here and hereafter,b:=|detA|.Throughout the whole paper,let σ be theminimum integersuch thatrσ≥2 and,for any subsetEof Rn,letE:=RnE.Then,for allk,j∈Z withk≤j,it holds true that

whereE+Fdenotes the algebraic sums{x+y:x∈E,y∈F}of setsE,F⊂Rn.

Definition 1 Aquasi-norm,associated with an expansive matrixA,is a Borel measurable mapping ρA:Rn→[0,∞),for simplicity,denoted by ρ,satisfying

(i)ρ(x)>0 for allx∈ Rnhere and hereafter, 0n:=(0,...,0);

(ii)ρ(Ax)=bρ(x)for allx∈Rn,where,as above,b:=|detA|;

(iii)ρ(x+y)≤Hρ(x)+ρ(y) for allx,y∈Rn,whereH∈[1,∞)is a constant independent ofxandy.

In the standard dyadic caseA:=2In×n,ρ(x):=|x|nfor allx∈ Rnis an example of homogeneous quasi-norms associated withA,here and hereafter,In×nalways denotes then×n unit matrixand|·|the Euclidean norm in Rn.

It was proved in[12,p.6,Lemma 2.4]that all homogeneous quasi-norms associated with a given dilationAare equivalent.Therefore,for a given expansive dilationA,in what follows,for convenience,we always use thestep homogeneous quasi-normρ defined by setting,for allx∈ Rn,

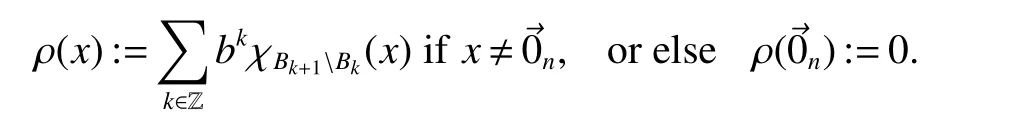
By(1)and(2),we know that,for allx,y∈Rn,

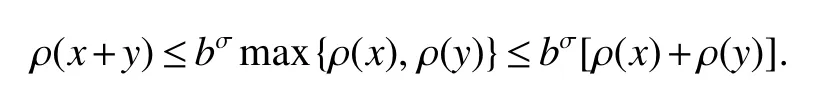
In what follows,we always let B:={z+Bk:z∈Rn,k∈Z}.

Definition 2 Letq∈ [1,∞).A function ϕ :Rn×[0,∞)→ [0,∞)is said to satisfy theuniform anisotropic Muckenhoupt conditionAq(A),denoted by ϕ ∈ Aq(A),if there exists a positive constantCsuch that,for allt∈ (0,∞)andB∈B,whenq∈(1,∞),

and,whenq=1,

Define A∞(A):=1≤q<∞Aq(A)and,for any ϕ∈ A∞(A),

If ϕ ∈ A∞(A)is independent oft∈ [0,∞),then ϕ is just an anisotropic Muckenhoupt A∞(A)weight in[13].Obviously,q(ϕ)∈ [1,∞).Moreover,it is known(see[6])that,ifq(ϕ)∈ (1,∞),then ϕ Aq(ϕ)(A)and there exists a ϕ∈(∩q>1Aq(A))A1(A)such thatq(ϕ)=1.

Now let us recall some notations for Orlicz functions;see,for example,[1].A function φ :[0,∞) → [0,∞)is called anOrlicz functionif it is nondecreasing,φ(0)=0,φ(t)>0 ift>0 and limt→∞φ(t)= ∞.Observe that,different from the classical Orlicz functions being convex,the Orlicz functions in this article may not be convex.

Given a function ϕ :Rn×[0,∞)→ [0,∞)such that,for anyx∈ Rn,ϕ(x,·)is an Orlicz function,ϕ is said to be ofuniformly type pwithp∈(−∞,∞)if there exists a positive constantCsuch that,for allx∈Rnandt,s∈(0,∞),

Now,we introduce the notion of anisotropicp-growth functions.

Definition 3 Letp∈(0,1].A function ϕ:Rn×[0,∞)→[0,∞)is called ananisotropic p-growth functionif

(i)The function ϕ is an Musielak-Orlicz function,that is,

(a)the function ϕ(x,·):[0,∞)→ [0,∞)is an Orlicz function for allx∈ Rn,

(b)the function ϕ(·,t)is a Lebesgue measurable function for allt∈ [0,∞);

(ii)the function ϕ belongs to A∞(A);

(iii)the function ϕ is of uniformly typep.

Clearly,

is an anisotropicp-growth function ifwis a classical or an anisotropic Muckenhoupt A∞weight([13])and Φ of uniformly typepfor somep∈ (0,1].Moreover,it is easy to see that if ϕ is an anisotropicp-growth function for somep∈(0,1],then ϕ is also an anisotropic growth function(see[6,Definition 3]).

Throughout the whole paper,we always assume that ϕ is an anisotropicp-growth function.Recall that theweak Musielak-Orlicz-type space Lϕ,∞is defined to be the set of all measurable functionsfsuch that,for some λ ∈ (0,∞),

with the weak(quasi-)norm

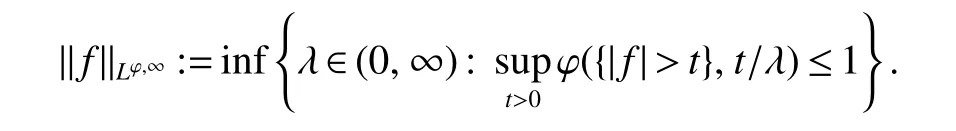
Form∈N,let

In what follows,for φ∈S,k∈Z andx∈Rn,let φk(x):=bkφ(Akx).

Forf∈S,thenon-tangential grand maximal functionoffis defnied by setting,for allx∈Rn,

If

where ϕ is ap-growth function andq(ϕ)as in(3),then we writef∗instead of.

Defniition 4 For anym∈N,p∈(0,1]and anisotropicp-growth function ϕ,theanisotropic weak Hardy spaceof Musielak-Orlicz type,,is defnied to be the set of allf∈Ssuch that∈Lϕ,∞with the(quasi-)norm:=Whenm:=m(ϕ),is denoted simply by.

Remark 1 (i)Observe that,whenA:=2In×nand ϕ is as in(5)with a Muckenhoupt(A∞(A))weightwand an Orlicz function Φ,the above weak Hardy spacesare just weak weighted Hardy spaces which include classical weak Hardy spaces of Fefferman and Soria[7](Φ(t):=tfor allt∈[0,∞)and ω≡1 in this context)and classical weak weighted Hardy spaces of Quek and Yang[8](Φ(t):=tpfor allt∈[0,∞)in this context).

(ii)When ϕ is as in(5)with Φ(t):=tpfor allt∈ [0,∞)and ω ≡ 1,the weak Hardy spacesbecome anisotropic weak Hardy spaces,which was introduce d by Ding and Lan[9].

Defniition 5 Let ψ∈S satisfyingRnψ(x)dx=0.For anyf∈ Sand λ∈ (0,∞),theanisotropic Littlewood-Paley Lusin-area function S(f),theanisotropic g-function g(f)and the(f),associated to ψ,are defnied,respectively,by setting,for allx∈Rn,

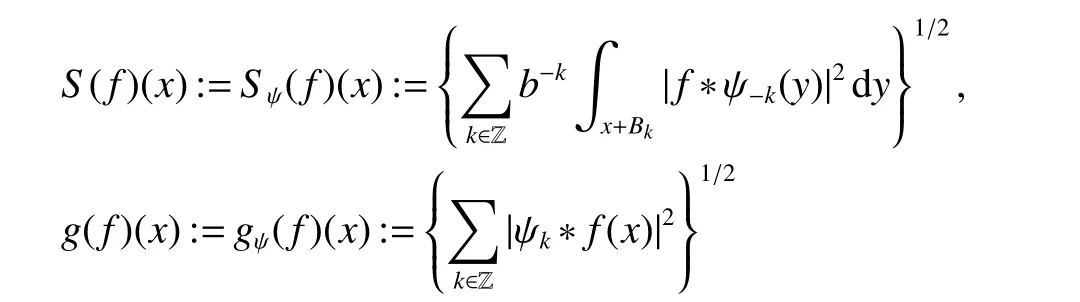
and

We now present our main results as follows.

Theo rem 1 Letp∈ (0,1],ϕ be an anisotropicp-growth function as in Defniition 3,m(ϕ)as in(6)and ψ ∈ S satisfying ψ(x)xαdx=0 for any|α|≤m(ϕ).Iff∈,thenS(f):=Sψ(f)∈Lϕ,∞andg(f):=gψ(f)∈Lϕ,∞and,

Rnmoreover,there exists a positive constantCindependent offsuch that

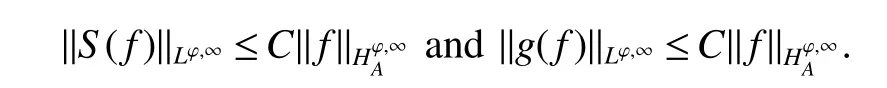
Theorem 2 Letp∈ (0,1],ϕ be an anisotropicp-growth function as in Definition 3,q(ϕ)as in(3),λ ∈(2q(ϕ)/p,∞),m(ϕ)as in(6)and ψ ∈ S satisfyingRnψ(x)xαdx=0 for any|α|≤m(ϕ).Iff∈,then(f)∈Lϕ,∞and,moreover,there exists a positive constantCindependent offsuch that

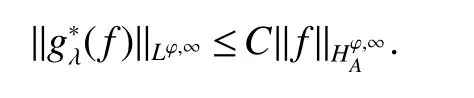
2 Proof of Theorem 1

In this section,we prove Theorem 1 by borrowing some ideas from[14,Theorem 1.1].Firstly,we need some lemmas.

Lemma 1 Letp∈ (0,1]and ϕ be an anisotropicp-growth function as in Definition 3.Then,given a positive constantc,there exists a positive constantCsuch that,for any λ ∈ (0,∞),the inequality supt>0ϕ({|f|>t},t/λ)≤cimpliesfLϕ,∞≤Cλ.

Proof By the condition of Lemma 1,we have,for any λ∈(0,∞),

which,together with the uniformly typepproperty of ϕ,we obtain,for any λ ∈ (0,∞),

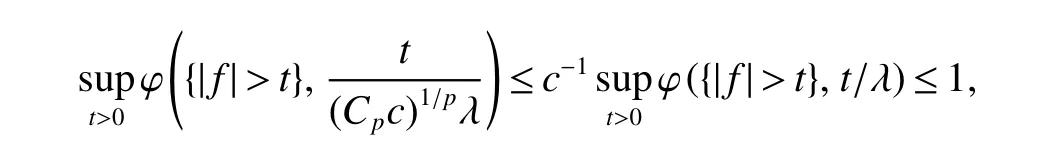
whereCpis a positive constant as in(4),and hence≤ (Cpc)1/pλ.Finally,Lemma 1 holds true by takingC=(Cpc)1/p.

The following Lemma 2 comes from[10,Theorem 2.6].

Lemma 2 Letp∈ (0,1]and ϕ be an anisotropicp-growth function as in Defniition 3.For anyf∈,there exist two positive constantsCandC1,and a sequence of bounded functions{fk}k∈Zwith the following properties:

(i)f=fkin SandfkL∞≤C2kfor everyk∈Z;(ii)eachfkmay be further decomposed asfk=also in S,where the functionssatisfy:

Conversely,iff∈Ssatisfying(i)and(ii),thenf∈.In addition,

In what follows,for any measurable functionfon Rn,q∈ [1,∞),ϕ ∈ Aq(A)and anyt∈ (0,∞),

By checking the proof of Theorem 3.2 in[15,pp.403-404],we obtain the boundedness of anisotropic Littlewood-Paley Lusin-area function on weighted Lebesgue spaces,which is the following Lemma 3.

Lemma 3 Let ϕ ∈ Aq(A)withq∈ (1,∞).Then there exists a positive constantCsuch that,for allf∈Lq(ϕ(·,t))andt∈(0,∞),

The following Lemma 4 comes from[16,pp.7-8].

Lemma 4 Letq∈[1,∞)and ϕ∈Aq(A).Then there exists a positive constantCsuch that,for allx∈Rn,k∈Z,E⊂(x+Bk)andt∈(0,∞),

By checking the proof of Lemma 2.16 in[17,pp.11-14],we have the following Lemma 5.

Lemma 5 Let σ ∈ Z+be as in(1),p∈ (0,1],ϕ an anisotropicp-growth function,m(ϕ)as in(6)and integersno less thanm(ϕ).Then,for any given functiona∈L∞with suppacontained in some dilated ballx0+Bkanda(x)xαdx=0 for any|α|≤s,there exists a positive constantCsuch that,for anyx∈x0+,

wherem∈ Z+satisfying ρ(x−x0)=bk0+σ+m.

The following Lemma 6 comes from[10,Lemma 3.5].

Lemma 6 Assume that the function:Rn×[0,∞)→ [0,∞)is of uniformly typeqwithq∈ (0,1)and{fk}k∈Na sequence of measurable functions satisfying

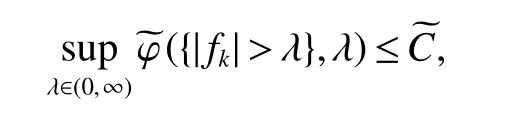
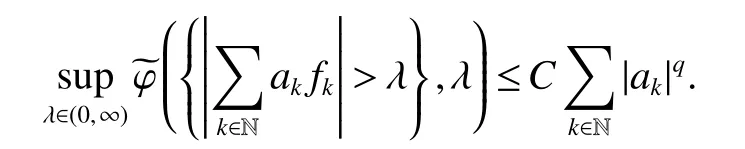
Proof of Theorem 1 Letp∈ (0,1],ϕ be an anisotropicp-growth function as in Defniition 3 andf∈.In order to proveby Lemma 1 with λ=,it suffices to prove supt>0ϕ({|S(f)|>t},t/) 1.And,by the uniformly typepproperty of ϕ,we only need to prove

For any givent∈(0,∞),choosingk0∈Z such that 2k0≤t<2k0+1.For anyf∈,by Lemma 2,we can write

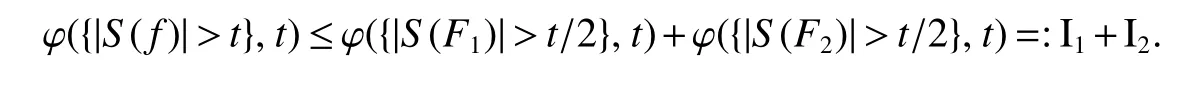
Letq(ϕ)be as in(3)andq∈(q(ϕ),∞).Firstly,we claim that the following inequality holds true:

Indeed,by Minkowski’s inequality,(a)and(b)of Lemma 2,t∼ 2k0,the uniformly typepproperty of ϕ andp/q−1<0,we obtain

Then,by Chebyshev’s inequality,Lemma 3 and(8),we obtain

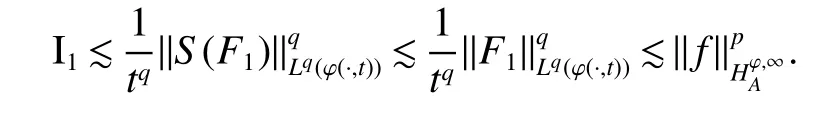
Now,we estimate I2.Let=:+with some∈Rnand∈Z,and

We then further decompose I2as

Thus,by Lemma 4,t∼2k0,the uniformly typepproperty of ϕ and Lemma 2(ii),we have

I2,1=ϕx∈Ak0:|S(F2)(x)|>t/2 ,t≤ϕAk0,t

Thus,in order to prove(7),it remains to estimate I2,2.Letsbe an integer no less thanm(ϕ)withm(ϕ)being as in(6).For anyx∈,by Lemma 5 withx∈+andm∈Z+satisfying ρ(x−)=,and Lemma 2(ii),we obtain

whereM:=(s+1)logb(λ−)+1.

Notice that,by the fact that(x,·)is nondecreasing uniformly for anyx∈ Rn,the uniformly typeq1property of,Lemma 4 with∈ Aqϕ(A)andqϕ

Letak,i:=(x)for anyx∈Rn.Then,by the uniformly typepproperty of ϕ,the assumption of Lemma 2(ii)(a)andq1

Furthermore,by the uniformly typeq1property ofand(11),we have,for anyt∈ (0,∞),

Thus,by Lemma 6 with(12)and(13),the uniformly typepproperty of ϕ,the assumption of Lemma 2(ii)(a),q1

From this and(10),it further follows that I2,2Combining the estimates of I1,I2,1and I2,2,we conclude that

3 Proof of Theorem 2

In this section,to prove Theorem 2,we first introduce the following variant of the anisotropic Lusin-area function and the anisotropic Hardy-Littlewood maximal function.For any fixedj∈ Z+and ψ ∈ S,f∈ S,thej-anisotropicLusin-area function and the anisotropic Hardy-Littlewood maximal function offare defined,respectively,by setting,for allx∈Rn,

The following Lemma 7 is just[17,Lemma 3.12].

Lemma 7 Letq∈[1,∞),ϕ∈Aq(A),j∈Z+,Ebe an open set in Rnand σ ∈Z+as in(1).IfU:=U j:= MA(χE)>b−2σ−jis the set associated toE,then,there exists a positive constantCsuch that,for allf∈ Sand λ∈(0,∞),

Lemma 8 Letq∈[1,∞),p∈(0,1]and ϕ∈Aq(A)be an anisotropicp-growth function as in Definition 3.Then there exists a positive constantCsuch that,for allj∈Z+andf∈S,

Proof For any λ∈(0,∞)andj∈Z+,letEλ,j:={S(f)>λbj/2}and

Then,by the weighted week type(q,q)of MAwithq∈[1,∞)and ϕ∈Aq(A)(see[13,Theorem 2.4]),we have

From this,by Chebyshev’s inequality and Lemma 7 withE:=Eλ,jandU:=Uλ,j,it follows that

To estimate I1,by the uniformly typepproperty of ϕ,we have I1bj(q−p/2)supλ∈(0,∞)ϕ({S(f)>λ},λ).To estimate I2,by the uniformly typepproperty of ϕ,we have,for all λ ∈ (0,∞),

Combining the estimates of I1and I2and the arbitrariness of λ∈(0,∞),we finish the proof of Lemma 8.

Lemma 9 Lett∈ (0,∞),p∈ (0,1]and ϕ be an anisotropicp-growth function as in Definition 3.SupposeT1andT2are two sublinear operators,fa measurable function andT2f∈Lϕ,∞{0}.Given a positive constantc,then there exists a positive constantCsuch thatimplies

Proof Lett∈ (0,∞).by the assumption of Lemma 9 and the definition of ·Lϕ,∞,we have

From this and Lemma 1,we deduce that

which implies that,fort1:=tT2fLϕ,∞,

which,together with Lemma 1,further implies thatT1fLϕ,∞T2fLϕ,∞.This finishes the proof of Lemma 9.

Proof of Theorem 2 Letp∈ (0,1],q(ϕ)be as in(3),λ ∈ (2q(ϕ)/p,∞),m(ϕ)as in(6)and ψ ∈ S satisfyingRnψ(x)xαdx=0 for any|α|≤m(ϕ).For allf∈Sandx∈Rn,we have

Letq∈ (q(ϕ),∞)close toq(ϕ)and ∈ (0,1)close to zero such that λ >2q/p+2 .Then,by(14),the uniformly typepproperty of ϕ,Lemma 8 andp−pλ/2+q<0,we have

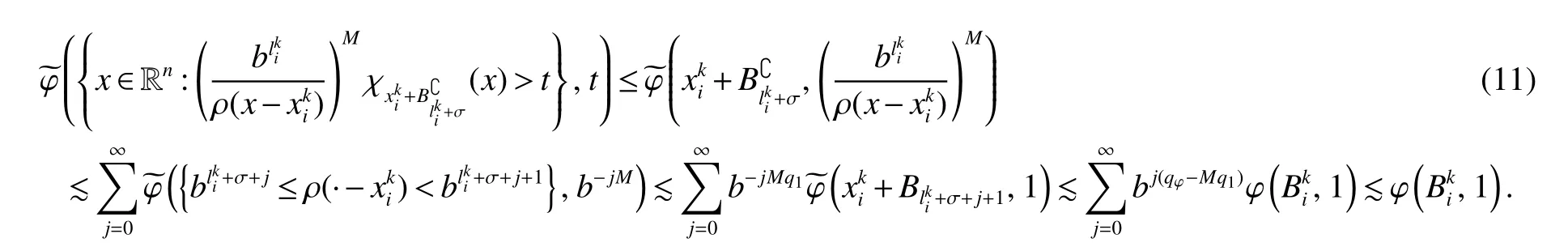
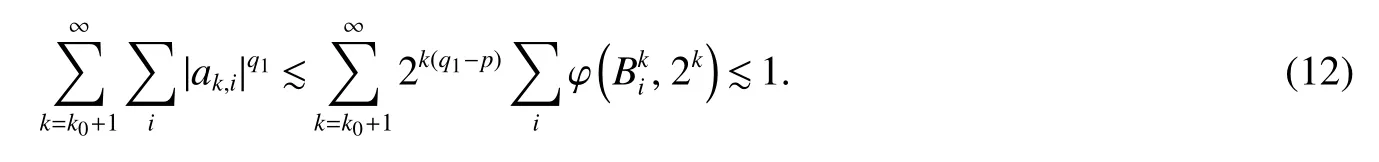
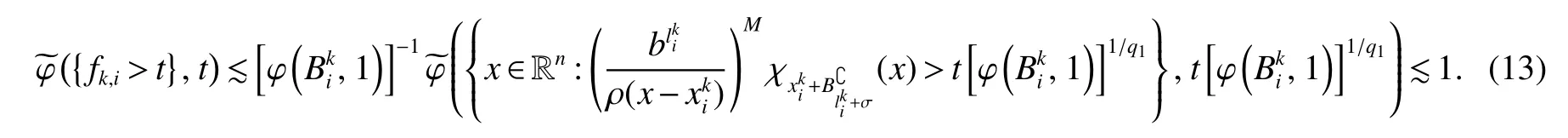
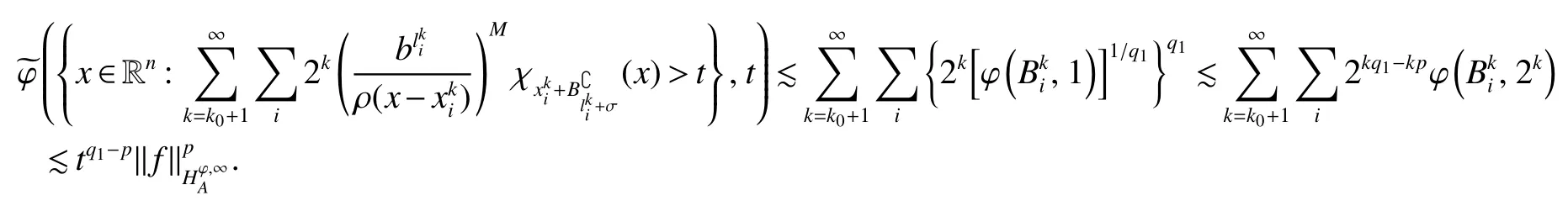
which,together with Lemma 9 and Theorem 1,we obtainThis finishes the proof of Theorem 2.