不对称布置多跨连续梁桥施工控制计算

王解军， 黄紫栋， 黄 佳

( 中南林业科技大学 土木工程与力学学院， 湖南 长沙 410004)



不对称布置多跨连续梁桥施工控制计算

王解军， 黄紫栋， 黄 佳

( 中南林业科技大学 土木工程与力学学院， 湖南 长沙 410004)

针对洞庭湖大桥君山侧副孔不对称5跨预应力混凝土连续梁桥，运用桥梁通用有限元软MIDAS/CIVIL软件，建立结构仿真计算模型，模拟箱梁施工过程，包括T构箱梁挂篮悬臂浇筑、边跨箱梁支架现浇及合拢、体系转换等全过程，考虑结构自重、预应力及混凝土收缩徐变等荷载，进行结构计算分析，得到了结构的应力与变形，为桥梁施工时主梁的线形和应力控制提供理论依据。

不对称连续梁桥； 施工过程，应力与变形； 有限元分析

1 概述

近年来，在我国道路交通建设的发展过程中，连续梁桥凭借其突出优点，得到广泛的运用。连续梁桥属于超静定结构，在恒活载作用下，产生的支点负弯矩对跨中正弯矩有卸载的作用，因此与同等跨径的简支梁桥相比，其跨中的正弯矩显著减小，从而跨越能力大。连续梁还具有结构刚度大、变形小、主梁变形挠曲线平缓、动力性能好及有利于高速行车等优点[1，2]。以往针对对称布跨的连续梁桥的理论研究、设计和施工研究较多，但关于不对称布置连续梁桥的研究成果较少。与对称布置连续梁桥相比，不对称连续梁桥在结构受力与变形上一般也存在不对称现象，给结构设计、施工及控制带来一定的难度与复杂性[3-6]。本文以洞庭湖大桥君山侧副孔桥为对象，分析研究不对称布置多跨连续梁桥的线形变化与应力，为桥梁施工控制提供理论依据。

2 工程概况

君山侧副孔桥为国家高速公路湖南省临湘(湘鄂界)至岳阳公路洞庭湖大桥的连接线工程，为预应力混凝土连续梁桥，位于湖南省岳阳市君山区。该桥由中交公路规划设计院有限公司设计。桥型为不对称布置多跨连续梁桥，主桥全长274.18 m，分5跨布置，桥跨布置为(32.18+4×60.5)m(见图1)。

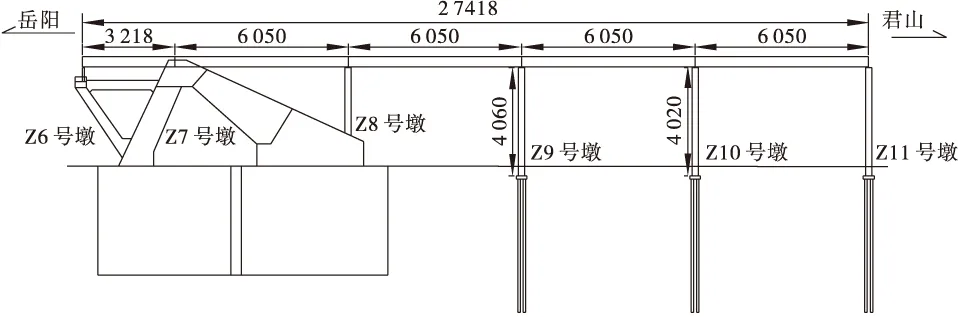
图1 主桥立面图(单位： mm)Figure 1 Elevation view of the bridge(unit： mm)

上部结构为60.5 m跨径的悬臂浇筑现浇预应力混凝土箱梁。主梁采用单箱单室截面，梁高3.65 m，高跨比为1/16.5。单幅箱梁宽度为16.3 m，底板宽6.5 m；箱梁翼缘悬臂长3.95 m，悬臂端厚度20 cm，悬臂根部厚度60 cm。箱梁顶板厚度标准段厚28 cm，近墩顶处加厚到60 cm。腹板采用变厚度设计，由近墩顶处100 cm厚渐变为70 cm厚，再变为跨中处50 cm厚。左侧边跨因长度较短，不存在50 cm厚腹板区段。底板标准段厚26 cm，近墩顶处加厚到65 cm。中间墩顶横隔板厚200 cm；小桩号侧端横隔板厚180 cm；大桩号侧横隔板厚230 cm。主梁采用纵、横向预应力体系；支座中心线距离箱梁底板中心的距离为2.3 m(沿底板)；箱梁底设置横桥向防落梁装置。

3 有限元模型

本次结构计算选用大型桥梁通用有限元软件MIDAS/CIVIL，考虑主桥平曲线与竖曲线，不考虑箱梁横坡与超高，根据设计图的施工阶段、结构布置和结构尺寸建立主桥的计算模型进行空间分析。主桥左右两幅主体结构布置基本相同，仅选择对左幅桥进行分析计算，右幅桥梁施工时，相关数据可参照左幅桥梁计算结果。对桥梁结构建立有限元模型(见图2)，主梁采用梁单元进行模拟，共划分为110节点，103个梁单元；主梁划分时，0#、1#节段均分为2个单元，2#～8#节段均分为1个单元，首跨现浇段分为4个单元，末跨现浇段分为11个单元，边跨合龙段和中跨合龙段均分为2个单元。在2#、15#、39#、63#、87#和110#节点处，建立弹簧单元模拟支座。

该桥采用挂篮悬臂施现浇法分段对称施工。0#、1#梁段采用托架施工法，2#～8#桥段采用挂篮悬臂浇筑，边跨搭设落地支架，拆除挂篮后，立模板浇筑边跨现浇段。主桥施工先合拢边跨，再合拢次中跨，最后合拢中跨。

图2 全桥有限元模型Figure 2 Finite element model of total bridge

4 计算结果分析

4.1 位移计算结果

以左幅Z08#墩为例，将桥梁上部结构悬臂施工时的最大悬臂阶段、合龙后以及二期恒载施工完成等关键施工阶段的竖向挠度绘制成曲线图进行对比分析。其中，边跨、中跨合龙后，则给出全桥竖向挠度曲线。在挠度曲线图中，横坐标表示结构节点，纵坐标表示挠度值，“+”表示位移向上、“-”表示位移向下，单位：mm，如图3～图10所示。

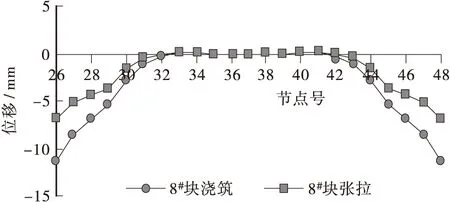
图3 最大悬臂施工阶段箱梁挠度Figure 3 The vertical deflection of box girder in extreme cantilever stage

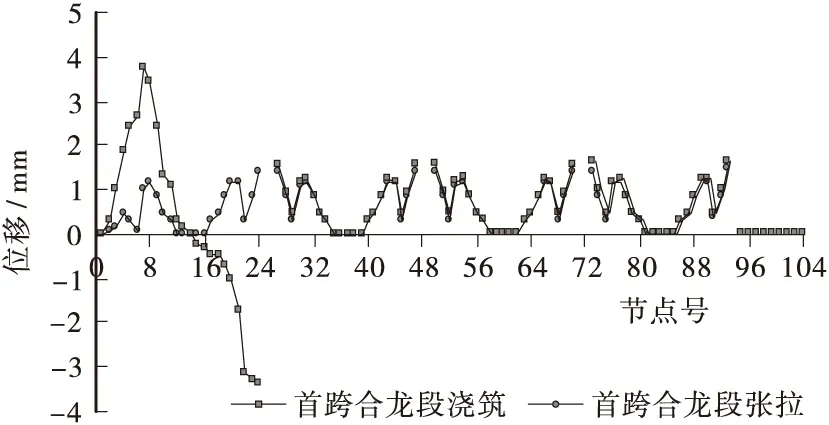
图4 首跨合龙后箱梁竖向挠度曲线Figure 4 The vertical deflection of box girder after first spans closure construction

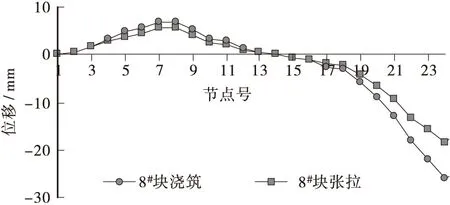
图5 8#梁段施工完毕后首跨及Z07墩右悬臂竖向挠度曲线Figure 5 The vertical deflection of box girder after 8# cantilever construction

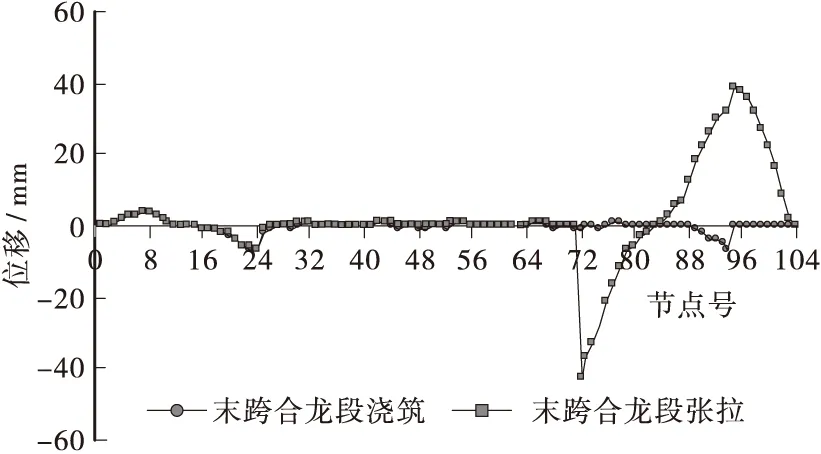
图6 末跨合龙后末跨及Z10墩左悬臂箱梁竖向挠度曲线Figure 6 The vertical deflection of box girder after last spans closure construction

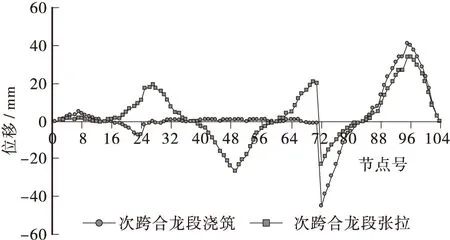
图7 次跨合龙后全桥箱梁竖向挠度曲线Figure 7 The vertical deflection of box girder after secondary spans closure construction

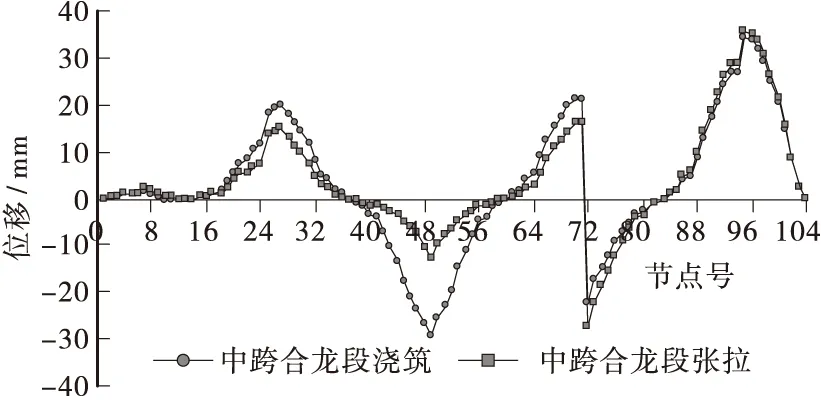
图8 中跨合龙后全桥箱梁竖向挠度曲线Figure 8 The vertical deflection of box girder after midspan closure construction

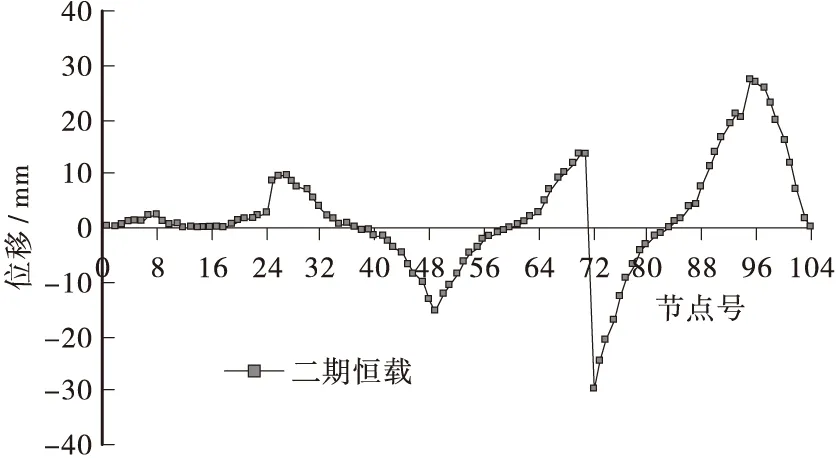
图9 二期恒载施工完毕后全桥箱梁竖向挠度曲线Figure 9 The vertical deflection of box girder after secondary permanent load construction

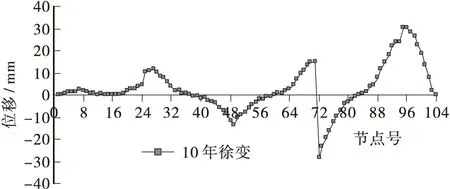
图10 10 a收缩徐变后全桥箱梁竖向挠度曲Figure 10 The vertical deflection of box girder after ten year shrinkage creep

由上述分析及图3～图10可以看出：

① 箱梁悬臂施工达到最大悬臂状态，即浇筑8#块时，梁端的竖向挠度达到-11.4 mm，张拉预应力后，梁端竖向挠度为-6.9 mm。

② 由于小桩号边跨无合龙段，施工过程采用先拆除挂篮，后张拉预应力，以及Z07#墩右悬臂施工8#块，导致Z07#墩右悬臂浇筑8#块时，梁端下挠达到最大值-25.9 mm，张拉预应力后，梁端挠度为-18.4 mm。

③ 上部结构施工完毕时，累计最大竖向挠度位于大桩号次跨跨中处，其值为-29.8 mm，最大竖向上挠位于大桩号边跨合拢段处，其值为27.3 mm；成桥后，计入10 a徐变作用，累计最大竖向挠度位于大桩号次跨跨中处，其值为-28.2 mm，最大竖向上挠位于大桩号边跨合拢段大里程方向附近截面处，其值为30.4 mm。

4.2 应力计算结果

采用悬臂法施工时，上部结构各关键部位应力随着梁段的伸展而累计增加。将桥梁主要施工阶段的结构应力曲线绘制如下，在悬臂施工阶段，以左幅Z08#墩为例；边中跨合龙后，则给出全桥各单元的应力曲线。在应力结果曲线图中，横坐标表示结构单元，纵坐标表示应力分析结果，“+”表示拉应力，“-”表示压应力。应力曲线如图11～图18所示。

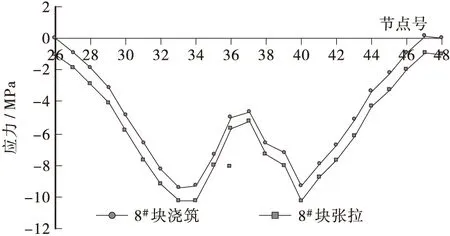
图12 最大悬臂状态箱梁下缘应力分布图Figure 12 The inferior margin stress of box girder in extreme cantilever stage

图13 次跨合龙后全桥箱梁上缘应力分布图Figure 13 The superior margin stress of box girder after secondary spans closure construction

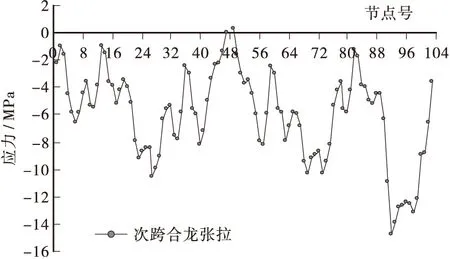
图14 次跨合龙后全桥箱梁下缘应力分布图Figure 14 The inferior margin stress of box girder after secondary spans closure construction

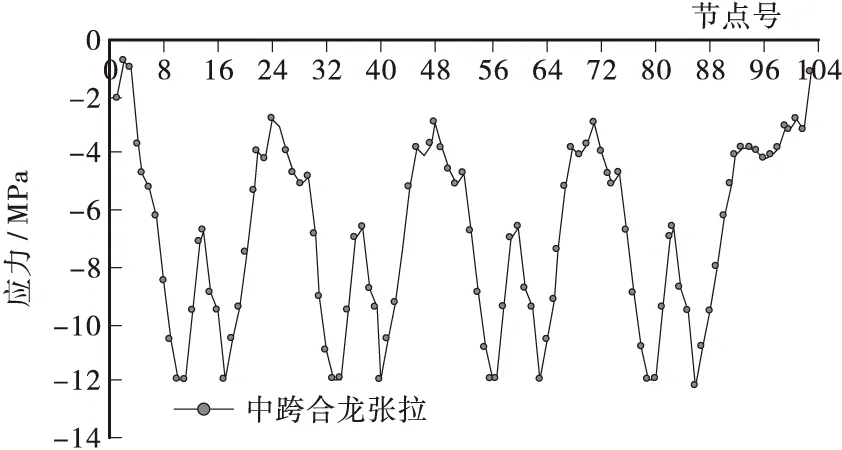
图15 中跨合龙后全桥箱梁上缘应力分布图Figure 15 The superior margin stress of box girder after midspan closure construction

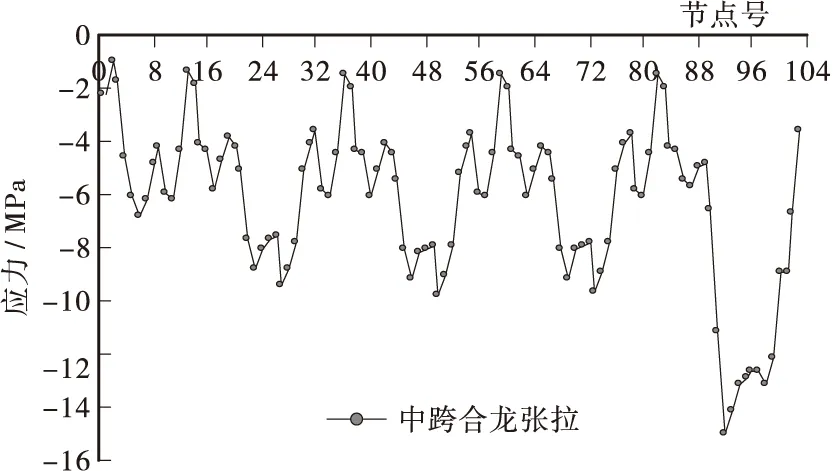
图16 中跨合龙后全桥箱梁下缘应力分布图Figure 16 The inferior margin stress of box girder after midspan closure construction

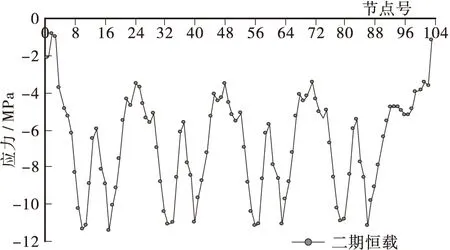
图17 二期恒载施工完毕后全桥箱梁上缘应力图Figure 17 The superior margin stress of box girder after secondary permanent load construction

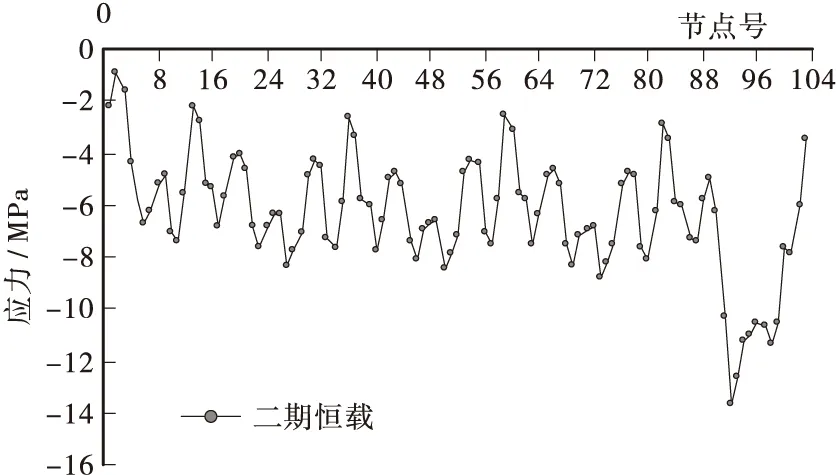
图18 二期恒载施工完毕后全桥箱梁下缘应力图Figure 18 The inferior margin stress of box girder after secondary permanent load construction

按照《公路钢筋混凝土及预应力钢筋混凝土桥涵设计规范》JTG D62 — 2004[7]第7.2.8条对施工阶段正截面法向应力进行验算，对于预应力混凝土受弯构件，在预应力和构件自重等施工荷载作用下截面边缘混凝土应力应满足：

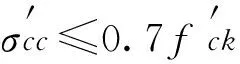
(1)

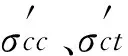
由图11～图18可知：

① 上部结构箱梁最大悬臂施工阶段，浇筑8#节段混凝土后，箱梁正截面最大压应力为-9.38 MPa，最大拉应力为0.11 MPa；8#节段张拉预应力后，箱梁正截面最大压应力为-10.30 MPa，最大拉应力为0.21 MPa，均符合JTG D62 — 2004第7.2.8条的相关规定，满足结构安全要求。

② 中跨合龙施工完毕后，箱梁正截面最大压应力为-15.00 MPa，最小压应力为-0.79 MPa，全截面均处于受压状态，符合JTG D62 — 2004第7.2.8条的相关规定，满足结构安全要求。

③ 二期恒载施工完毕，即上部主体结构施工完毕后，箱梁正截面最大压应力为-13.70 MPa，最小压应力为-0.93 MPa，全截面均处于受压状态，符合JTG D62 — 2004第7.2.8条的相关规定，满足结构安全要求。

5 结论

通过以上对主桥结构的计算结果可以看出：

① 在浇筑8#块时，箱梁悬臂施工达到最大悬臂状态，由于小桩号边跨无合龙段，使梁端下挠达到最大值。在次跨、中跨合拢工况，预应力钢绞线的张拉产生的预应力对箱梁挠度的变化起主导作用，使得合拢段梁体上挠，最大竖向上挠位于大桩号边跨合拢段处。

② 计算结果表明，在悬臂施工阶段，箱梁截面应力都处在规范规定的范围内，在中跨合拢和二期恒载施工完毕后，全截面处于全压状态，具有一定的压应力储备，整个上部结构处于安全状态。

[1] 姚玲森.桥梁工程( 第二版)[M].北京: 人民交通出版社，2008.

[2] 王解军，周先雁.大跨桥梁[M]．北京: 北京大学出版社，2012.

[3] 汤崇菊,邓磊. 不对称跨径的连续梁桥静动载试验研究[J].铁道建筑,2014(08)：17-19.

[4] 杜荣生.非对称连续梁桥设计及结构内力优化[J].公路交通科技,2015(11)；147-148.

[5] 黄晓东,祝哨晨,周焱,等.连续梁桥中跨与边跨不对称施工的线形控制[J].中国市政工程,2007(5):21-23.

[6] 夏风波.大跨径不对称预应力混凝土连续梁桥设计[J].中国水运，2010(10):221-222 .

[7] JTG D62-2004,公路钢筋混凝土及预应力钢筋混凝土桥涵设计规范[S] .

[8] Chen Mengcheng,Gu Zhangchuan. Monitoring Technology for Multi-span Continuous Beam Bridge Construction[J].Urban Mass Transit,2012(5)61-64.

[9] 骆佐龙,董峰辉.连续梁桥悬臂施工状态可靠度分析[J].公路工程，2013,38(03):162-164.

[10] 王志诚,许春荣.大跨度钢连续梁线形几何控制法[J].公路工程，2012,37(05):156-160.

[11] JTG/T F50-2011,公路桥涵施工技术规范[S].

The Construction Control Calculation of The Asymmetry Layout Multi-span Continuous Girder Bridge

WANG Jiejun, HUANG Zidong, HUANG Jia

( College of Civil Engineering and Mechanics，Central South University of Forestry and Technology，Changsha，Hunan 410004，China)

For the asymmetric 5 span prestressed concrete continuous Girder bridge of the Junshan side of the Dongting Lake bridge, based on the general finite element software MIDAS/CIVIL, the structural simulation model is established, and the whole process of box girder construction is simulated, including the T frame box girder cantilever hanging basket casting, cast-in-place and closure up of the side span box girder, system transformation. Then considering the load of the structure, such as the weight of the structure, the shrinkage and creep of the concrete,the stress and deformation of the structure are calculated and analyzed, which provides a theoretical basis for the linear and stress control of the main beam in bridge construction.

asymmetric continuous girder bridge; construction process; stress and deformation; finite element analysis

2016 — 07 — 29

王解军(1963 — )，男，湖南邵阳人，教授，博导，主要从事大跨与复杂桥梁结构理论及新技术研究。

U 448.21+5

A

1674 — 0610(2016)05 — 0147 — 04