钢管加固既有短柱桥墩轴压承载力计算研究

刘金升， 钱永久

(西南交通大学 土木工程学院， 四川 成都 610031)



钢管加固既有短柱桥墩轴压承载力计算研究

刘金升， 钱永久

(西南交通大学 土木工程学院， 四川 成都 610031)

采用外套钢管加固既有钢筋混凝土柱是工程中常用的加固技术，国内外对其加固后结构的承载力计算理论研究较少。针对情况1(原柱混凝土在加固前完全卸载或初始应力较低)从极限平衡理论的角度出发分析加固构件的受力特征，推导出短柱桥墩加固后结构的轴压承载力的计算公式，并与试验的数据相对比，两者符合较好，可为工程实际加固墩柱承载力计算分析提供支持。

极限平衡法； 桥梁加固； 钢管加固； 桥墩

0 引言

钢管外套加固钢筋混凝土柱的加固技术是工程加固中常用的加固技术手段，但目前这种加固技术在加固结构承载力计算研究发面存在滞后性，在《公路桥梁加固设计规范》和《混凝土结构加固设计规范》中没有钢管外套混凝土加固结构的承载力计算方法及受力分析。

本文在总结钢管混凝土和局压钢管混凝土的承载力计算相关研究的成果基础上，运用极限平衡法推导轴压加固结构的承载力计算公式，为工程实践提供指导借鉴。

1 极限平衡理论计算与分析

1.1 情况1加固结构基本假定

① 轴心受压的核心混凝土柱的应变场是轴对称的，填充混凝土与核心混凝土间完全粘结无滑移。钢管和填充混凝土、核心混凝土的极限屈服条件都是稳定的；钢管采用Von Mises屈服准则，三向受压混凝土屈服条件采用Сonsidere和Richartd的实验线性公式(1)和根据实验资料蔡绍怀建议非线性公式(2)，如下所示。

σc=fc+kp

(1)

(2)

式中：σc为三向受压混凝土抗压强度；fc为混凝土无侧压强度；p为侧压力，k为侧压系数。

② 加固结构在原柱上施载，经原柱混凝土压力扩散后结构受力与局压钢管混凝土相似，对加固后结构采用KLCO为局压承载力折减系数:KLCO=A·β+B·β0.5+C[8]，具体参数含义见文献。原柱钢筋为简化计算，只考虑加固结构极限状态时，原柱钢筋为屈服状态。

1.2 情况1加固结构承载力计算公式推导

用静力法求解，钢管、填充混凝土、核心混凝土的受力如简图1～图4。

由图1建立静力平衡条件建立方程，即：

N=KLCO(Ac1σc1+Ac2σc2+Asσ1)+As1σs1

(3)

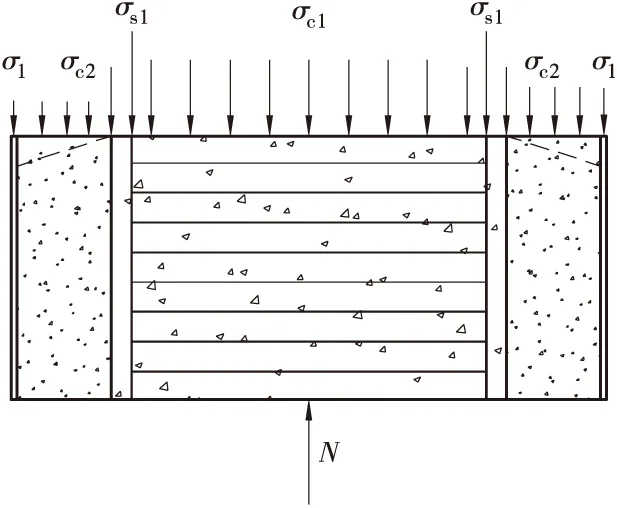
图1 加固柱纵向承载受力简图Figure1 Free-body diagram of longitudinal reinforcement column

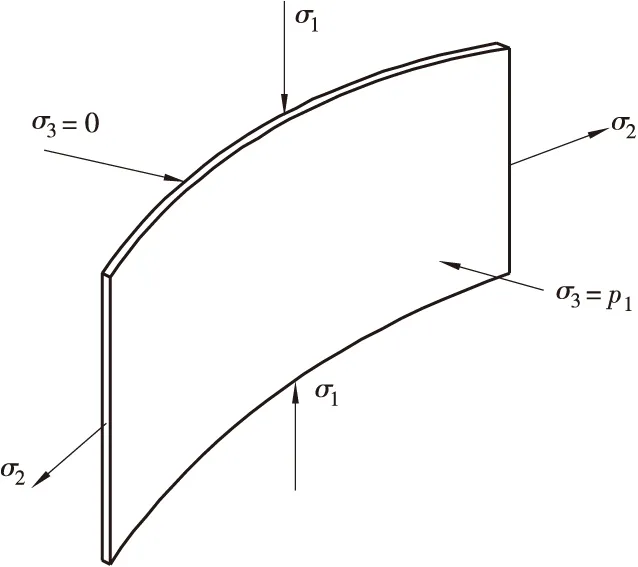
图2 钢管微元受力图Figure 2 Steel tube infinitesimal body

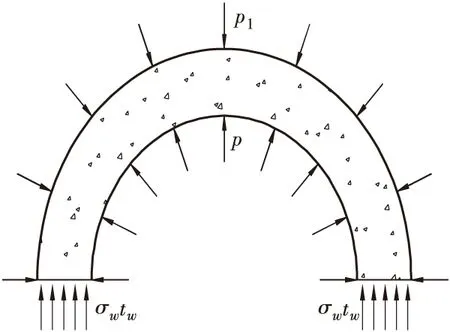
图4 填充混凝土受力简图 Figure 4 Force diagram of filled concrete

其中：Ac1、Ac2、As、As1分别为核心混凝土、填充混凝土、钢管、纵筋横截面积，σc1、σc2、σ1、σs1分别为核心混凝土、填充混凝土、钢管、纵筋纵向应力，fs为钢管的屈服极限，tw和t为填充混凝土和钢管厚度，dc和dz为核心混凝土柱和加固后混凝土直径。p1为填充混凝土对钢管的径向应力，p为核心混凝土对填充混凝土的径向应力，fy1为纵筋的屈服强度。

由图3建立静力平衡方程可得：

(4)

由(4)式可求得：

(5)

对填充混凝土，由图4建立静力平衡方程可得：

(6)

整理(6)可得：

(7)

加固结构中，填充混凝土强度一般较原柱混凝土的强度等级高一两个等级，填充混凝土因受施加在核心柱上混凝土的轴向力的压力扩散，同时受钢管的约束而处于三向受压状态。由图4对式(7)取σw=p1，则求得：p=p1

(8)

由图2钢管的Von Mises屈服条件得：

(9)

由式(5)和式(9)可得：

(10)

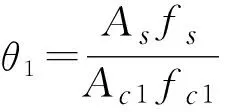
取核心和填充混凝土的屈服条件为式(1)，代入式(3)得：

N=KLCO(Ac1σc1+Ac2σc2+Asσ1)+As1σs1=

As1σs1

(11)

荷载N是侧压力p的函数，为求最大的荷载Nmax，对荷载N取p的导数，则dN/dp=0，则：

(12)

在本文中k的取值为k=4，则得：

(13)

加固结构处于极限状态时，钢筋为屈服状态，把式(13)代入式(12)得：

(14)

下面取混凝土屈服条件为非线性方程(2)并整理式(3)得：

As1σs1

(15)

荷载N是侧压力p的函数，同样为求最大的荷载由dN/dp=0，求得：

(16)

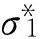
(17)

从而可以得到加固后结构的极限承载力式(15)的近似计算值为：

As1fy1

(18)

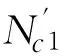
(19)

(20)

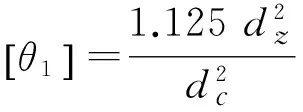
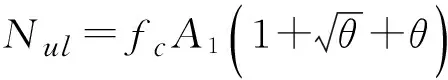
As1fy1

(21)

2 实验算例

2.1 试件的制作及材料性能

为得到加固结构混凝土的极限承载力，做了试验研究。试验中制作了4根钢筋混凝土短柱，其中一根为原墩柱，其它3根是不同厚度的外套钢管加固混凝土柱的加固试件。加固试件的尺寸见表1。

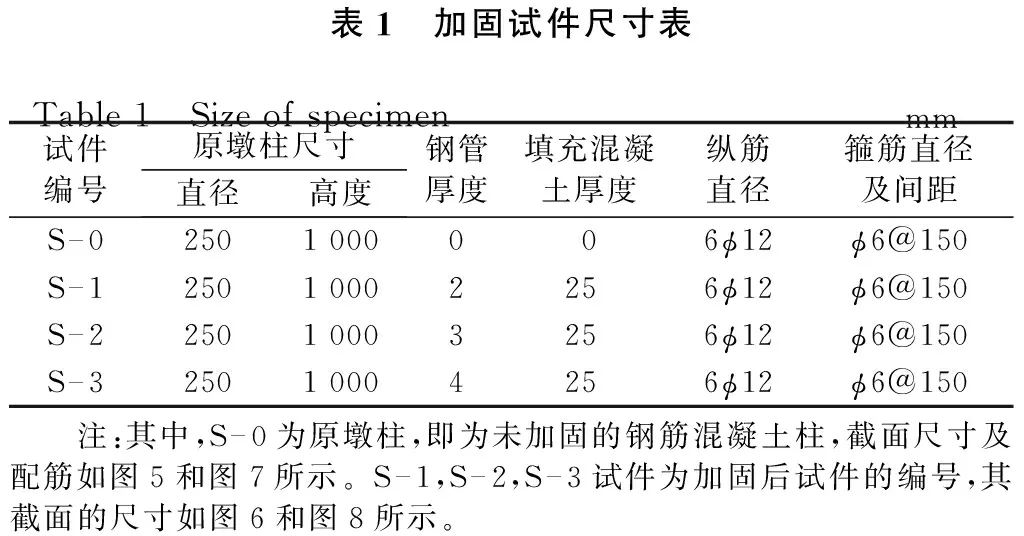
表1 加固试件尺寸表Table1 Sizeofspecimenmm试件编号原墩柱尺寸直径高度钢管厚度填充混凝土厚度纵筋直径箍筋直径及间距S—02501000006ϕ12ϕ6@150S—125010002256ϕ12ϕ6@150S—225010003256ϕ12ϕ6@150S—325010004256ϕ12ϕ6@150 注:其中,S—0为原墩柱,即为未加固的钢筋混凝土柱,截面尺寸及配筋如图5和图7所示。S—1,S—2,S—3试件为加固后试件的编号,其截面的尺寸如图6和图8所示。

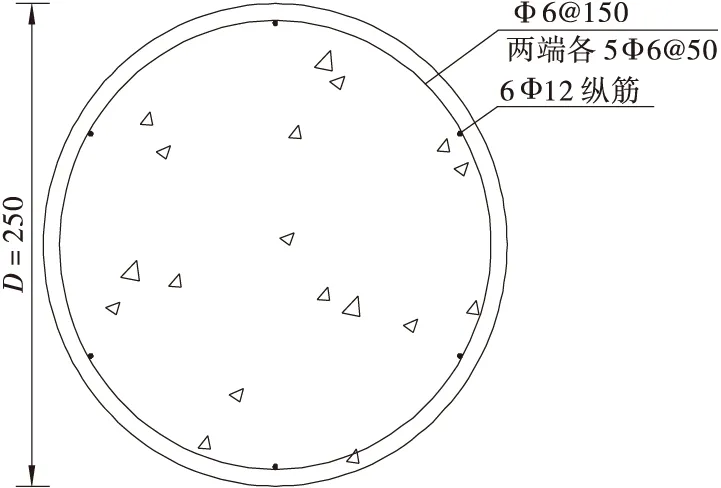
图5 原墩柱的截面示意图Figure 5 Section pier column arrangement

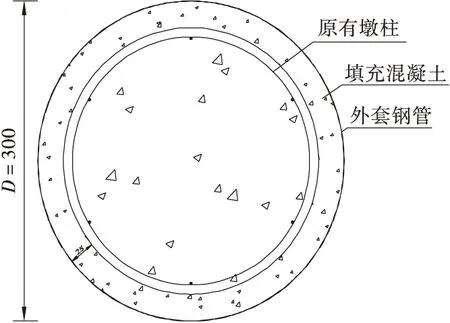
图6 加固后结构截面示意图Figure 6 The reinforcement structure section arrangement

图7 原墩柱的配筋图 图8 加固后结构钢管布置图

Figure 7 Pier reinforcement arrangement Figure 8 Structural steel reinforcement arrangement

填充混凝土为立式浇灌，试验试件的原柱混凝土和填充混凝土强度均是由在实验室中相同条件测得。其混凝土强度测试尺寸为150 mm的立方体试块。

原柱和填充混凝土试件的材料强度见表2。

试验加固试件外套钢管为Q235钢板经卷板机卷曲后焊接而成，外套钢管的材料性能是根据外套钢管的厚度不同截取原材料做拉伸试验和焊接板拉伸试验。原柱纵筋与箍筋同样由预留的试件截取得到，按《金属拉伸试验方法》进行材性测试，外套钢管和钢筋力学性能见表3所示。

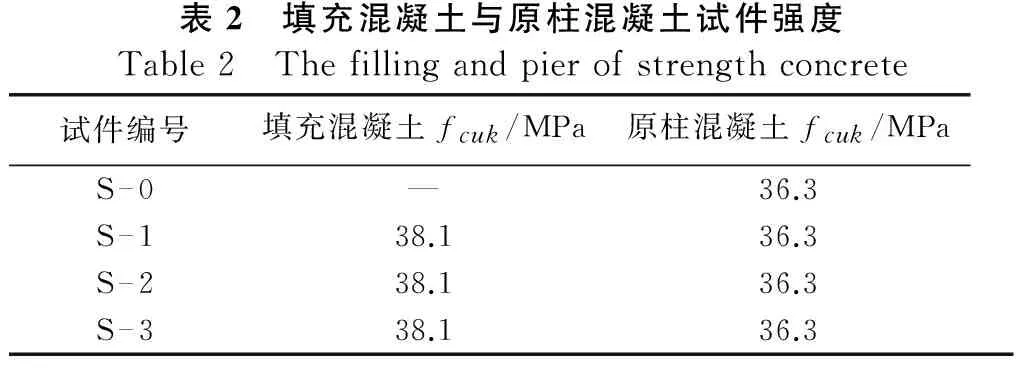
表2 填充混凝土与原柱混凝土试件强度Table2 Thefillingandpierofstrengthconcrete试件编号填充混凝土fcuk/MPa原柱混凝土fcuk/MPaS—0—36.3S—138.136.3S—238.136.3S—338.136.3

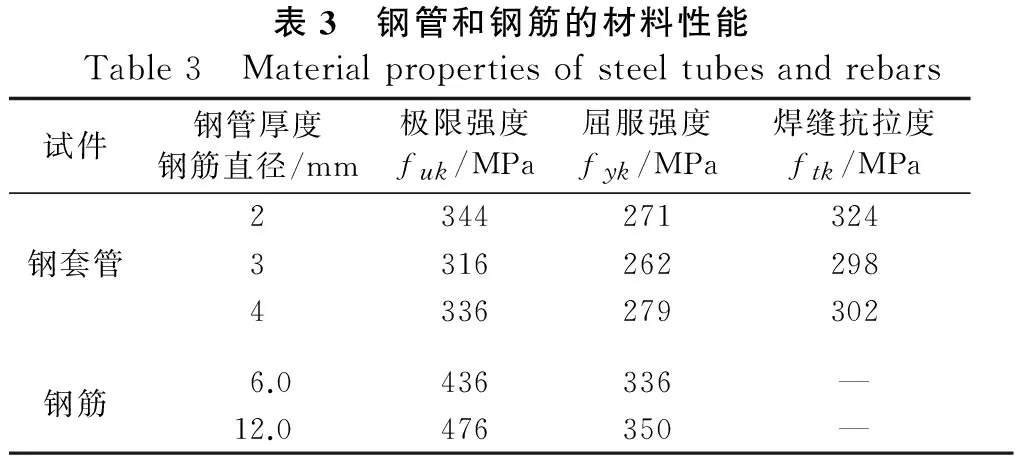
表3 钢管和钢筋的材料性能Table3 Materialpropertiesofsteeltubesandrebars试件钢管厚度钢筋直径/mm极限强度fuk/MPa屈服强度fyk/MPa焊缝抗拉度ftk/MPa2344271324钢套管33162622984336279302钢筋6.0436336—12.0476350—

原钢筋混凝土柱是在实验室中配筋浇筑成型4根钢筋混凝土柱试件。加固试件是在原钢筋混凝土墩柱浇筑成型自然养护直至试验，试验前对3根混凝土柱表面凿深6 mm左右凹凸面后用高压水枪冲洗，然后用钢管焊接套箍加固，在原墩柱和钢筋混凝土柱之间浇灌填充混凝土。制作部分过程如图9所示。

(a) 钢筋绑扎笼(b) 钢筋混凝土柱成型

(c) 焊接外套钢管(d) 加固试件浇灌完成

2.2 试验加载装置和加载程序

外套钢管加固钢筋混凝土柱的轴压承载力试验是在西南交通大学实验室的长柱试验机上完成的，试件上下两端为钢垫板，试件在对称面各装一个位移计，如图10所示。

具体的试验加载程序为：

① 在试验前准备好放置好试件，把试件的两端找平，准备初始数据的记录。

图10 实际加载图Figure 10 Loading deviee

② 开动试验机，当压头与试件将要接触时，再次对试件调整找平。

③ 在试验正式开始前，对试件进行预加载，同时查看试验机的运行情况。加载程序如图11所示。正式加载时采用是逐步分级加载，每级所加的荷载基本为破坏荷载的10%，每级加载完成以后，稳定停留5 min后进行下一级的加载，当荷载加载到90%的破坏荷载以后，按每级荷载的5%增量加载，逐步加载到试件破坏为止。

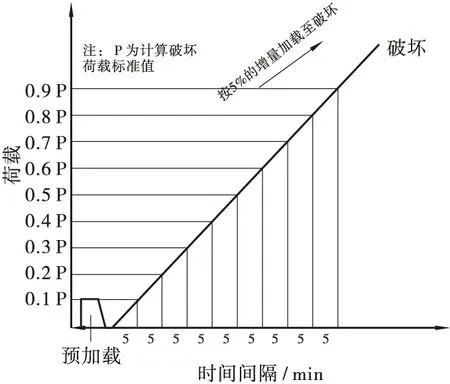
图11 加载程序Figure 11 Loading program

2.3 试件的破坏形态及极限承载力实测值和计算结果对比

图12为各试件轴心受压后的破坏形态及破坏特征。

S — 0试件的破坏形态，同一般的钢筋混凝土柱破坏形态，破坏时混凝土压溃，混凝土保护层脱落。S — 1试件破坏时，试件上部外鼓，中部亦出现外鼓现象，套管面出现滑移线。S — 2试件破坏时，试件外鼓，表面出现滑移线，套管焊缝开裂，混凝土有压碎现象。S — 3试件破坏时，试件轻微外鼓，管内的填充混凝土和原柱混凝土压碎，套管焊缝有开裂现象。

(a) S-0(b)S-1

(c) S-2(d) S-3

通过试验得到的加固后的墩柱的极限承载力实测值如表4所示。

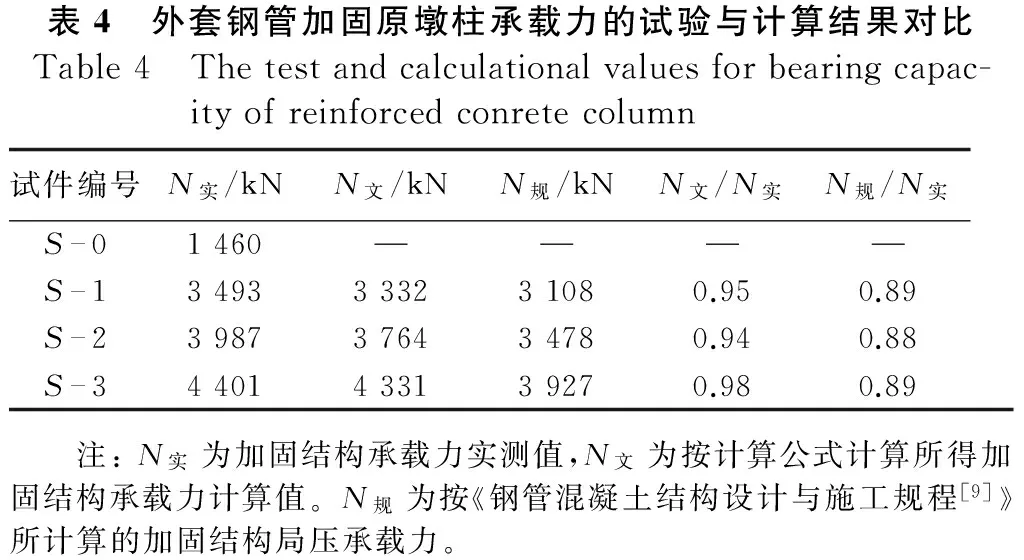
表4 外套钢管加固原墩柱承载力的试验与计算结果对比Table4 Thetestandcalculationalvaluesforbearingcapac-ityofreinforcedconretecolumn试件编号N实/kNN文/kNN规/kNN文/N实N规/N实S—01460S—13493333231080.950.89S—23987376434780.940.88S—34401433139270.980.89 注:N实为加固结构承载力实测值,N文为按计算公式计算所得加固结构承载力计算值。N规为按《钢管混凝土结构设计与施工规程[9]》所计算的加固结构局压承载力。

表4表明： 加固结构承载力N文/N实∈(0.94,0.98)，本文计算公式结果与试验结果符合较好，是良好的钢管外套钢筋混凝土柱结构承载力计算方法。同时表中加固试件S — 1、S — 2、S — 3与未加固S — 0试件承载力对比可看出加固试件的承载力明显提高。

从表4中可看出: 本文的计算公式的计算结果优于按《钢管混凝土结构设计与施工规程》所计算的承载力的结果，更接近于试验的实测值。对于N规相对于实测值有较大差异主要是由于，其局压承载提高系数采用的同一般螺旋套箍混凝土相同系数，相对过于保守，而且其承载力计算中不能完全体现填充混凝土的强度对于加固结构承载力的贡献。虽然N规与试验结果有一定差异，但N规可以作为计算情况1外套钢管加固钢筋混凝土柱结构承载力的一种参考。

3 结论

本文通过对外套钢管加固钢筋混凝土短柱承载力的计算公式推导及实验研究，得出如下结论：

① 说明本文的加固结构极限承载力计算结果与实验数据符合较好，是良好的钢管外套钢筋混凝土柱结构承载力计算方法。

② 本文中定义θ1套箍指标为外套钢管对原有核心柱的套箍指标，此定义使外包钢管对核心混凝土柱的套箍作用显示更直观，同时可以区分钢管内原有柱混凝土和填充混凝土各自对加固结构承载力的贡献。本文的计算公式根据力学平衡条件推导得出，因此加固结构计算承载力力学概念清晰实用范围更通用。

③ 本文的计算公式的计算结果优于按《钢管混凝土结构设计与施工规程》所计算的承载力的结果。同时表明对本文加固结构不能按局压钢管混凝土计算其承载力，但N规可以作为计算情况1外套钢管加固钢筋混凝土柱结构承载力的一种参考。

[1] 韩林海，杨有福.现代钢管混凝土结构技术[M]，北京：中国建筑工业出版社，2004:77-91.

[2] 钟善桐.钢管混凝土结构[D].北京：清华大学出版社,2003: 231-268.

[3] 蔡绍怀.现代钢管混凝土结构[M].北京：人民交通出版社,2003:35-56.

[4] 蔡绍怀，焦占拴.钢管混凝土短柱的基本性能和强度计算[J].建筑结构学报,1984(6):13-29.

[5] 袁文伯译.极限平衡法的结构承载能力的计算[M].北京：建筑工程出版社,1958.

[6] Kato B. Column curves of steel-concrete composite members. Journal of Constructional Steel Research,1996.

[7] McAteer P, Bonacci J F, Lachemi M. Composite response of high-strength concrete confined by circularsteel tube. ACI Structural Journal,2004.

[8] 刘威.钢管混凝土局部受压时的工作机理研究[D].福州:福州大学，2005.

[9] CECS28:90,钢管混凝土结构设计与施工规程[S].

Research on Bearing Capacity of External Steel Tube Reinforced Existed Ferroconcrete Column

LIU Jinsheng, QIAN Yongjiu

(School of Civil Engineering, Southwest Jiaotong University, Chengdu, Sichuan 610031, China)

The existed concrete column reinforced by external steel tube is a common reinforcement technique and widely used in engineering. However, the computational theory on bearing capacity of the reinforced structure is insufficient at present. In the condition that completely unloading before the existed column concrete is reinforced or the initial stress level is low, the mechanics characteristics of reinforced components are analyzed based on the limit equilibrium method, and then the computational equations of the bearing capacity subjected to axial loading after the short column pier reinforced of structure have been deduced. Comparing the calculation results with the correspondent experimental data shows that the deduced equation can provide a reasonable result for predicting the axial bearing capacity, which provides a support for the computation of the bearing capacity for the reinforcement pier in practice.

limit equilibrium method; bridge reinforcement; steel tube reinforcement; bridge piers

2015 — 04 — 10

刘金升(1979 — )，男，辽宁瓦房店人，博士研究生，主要从事桥梁的维修和加固研究。

U 445.7+2

A

1674 — 0610(2016)05 — 0107 — 06