超声波法评估杉木原木力学性能研究

张 甜， 程小武， 陆伟东， 刘伟庆

(南京工业大学 土木工程学院， 江苏 南京 211816)



超声波法评估杉木原木力学性能研究

张 甜， 程小武， 陆伟东， 刘伟庆

(南京工业大学 土木工程学院， 江苏 南京 211816)

木材的力学性能是反映木材利用价值的重要指标，为了探讨超声波法评估原木力学性能的可行性，利用传统的力学试验机对杉木原木的顺纹抗压强度(σc)、抗拉强度(ft)、抗弯强度(σb)、抗压弹性模量(Ec)进行测试，利用实验室方法对杉木的密度(ρ)也进行测试；采用超声波法测试了杉木试件的动弹性模量(Eus)。分析了动态弹性模量和静态抗压弹性模量之间的差异，研究了顺纹抗压强度(σc)、抗拉强度(ft)、抗弯强度(σb)、静弹性模量(Ec)与动弹性模量(Eus)、密度(ρ)之间的关系。结果表明： ①超声波法获得的动弹性模量值稍大于静态抗压弹性模量。 ②密度与顺纹抗压强度(σc)、抗拉强度(ft)、抗弯强度(σb)、静态弹性模量(Ec)有一定的相关性。 ③动弹性模量(Eus)与顺纹抗压强度(σc)、抗拉强度(ft)、抗弯强度(σb)、静态弹性模量(Ec)也存在一定的相关性，且相关性要高于前者。

杉木； 超声波； 动弹性模量； 力学性能

0 前言

木材是一种良好的弹塑性材料，且由于质量轻及耐冲击等特点，成为人类最早使用的建材之一。作为一种重要的建筑材料，不仅加工能耗少，且环境污染小，是当今社会可持续发展战略构想的理想材料[1]。我国现存许多传统的木结构建筑，在古建筑维修和保护过程中，首先应对木构件材料的力学性能进行科学评估。无损检测是根据材料不同的物理或化学性质，在不破坏目标物体内部及外观结构与特性的前提下，对物体相关特性(如形状、位移、应力、光学特性、流体性质、力学性质等)进行检测[2]，研究发现应力波、超声波、振动法断层成像技术等无损检测方法在木质材料检测领域具有显著的优势[3，4]。

目前检测木构件力学性能的方法是采用实验室方法对木材各项力学性能进行测试，但是这种方法检测时间长、条件苛刻、稳定性差。因此在古建筑木结构的修缮维护过程中，如何能在不破坏木构件内部结构和外部特征的前提下，探索出一项快速的、科学的无损检测技术已经成为古建筑维护过程中亟待解决的问题。

国外学者对超声波检测木质材料进行了较多的研究，Almir Sales[5，6]对巴西的典型树种进行了研究，发现木材密度、抗弯弹性模量与超声波传播参数有显著的相关性。José Saporiti Machado[7]，Abel Vega[8]利用超声波无损检测法对木材的抗弯性能进行了检测，研究发现木材的弹性模量与超声波的传播参数相关性显著。近几年，国内学者对超声波检测木材力学性能的研究也进行了一系列的研究，罗彬[9]分别采用了超声波法、应力波法和纵向基频振动法对巨尾桉木材进行了检测，分析了三种动弹性模量与木材顺纹抗压强度、抗弯强度、抗弯弹性模量的关系。张训亚[10]、殷亚芳[11]等人利用超声波法评估了人工林杉木、落叶松的抗弯性能。王立海[12]以色木方才作为研究对象，利用超声波、应力波、纵向共振方法对木材动弹性模量进行检测，发现三种动弹性模量均高于实验室测试得到的静弹性模量，但是两者之间存在明显的相关性。但应用超声波评估结构用原木力学性能的研究较少。

本文以南方常用树种——杉木原木为研究对象，采用超声波法对其各项力学性能进行了检测评估，首先，利用超声波间接测试方法对杉木的动态弹性模量进行检测；其次，根据《木材密度测定方法》(GB1933-2009)、《木材顺纹抗压强度试验方法》(GB/T 1935-2009)、《木材抗弯强度试验方法》(GB/T 1936.1-2009)、《木材顺纹抗拉强度试验方法》(GBT 1938-2009)、《木结构试验方法标准》(GB/T 50329-2012)等相关标准对试件的各项指标进行测定；最后对各项力学性能指标与密度、动弹性模量的相关性进行分析，建立相应的计算模型，旨在探讨利用超声波法评估原木力学性能的可行性。

1 材料与方法

1.1 材料

杉木取自安徽宣城，原木直径范围为15～18 cm，原木长度均为4 m。在实验室将4 m长的杉木原木进行去皮处理，将原木锯成长为40 cm的试件65个(见图1)，气干至平衡含水率，处于试验状态。

图1 试验材料Figure 1 Test materials

1.2 方法

1.2.1 动态弹性模量测试

超声波法检测方法有很多种，本文采用超声波脉冲穿透法进行测试，使用的仪器为瑞士生产的Sylvatest-Duo超声波木材检测仪(见图2)，超声波法是根据超声波在木材中的传播速度计算动弹性模量的。动态弹性模量的计算公式为：

E=ρV2

(1)

图2 Sylvatest-Duo木材检测仪Figure 2 Sylvatest-Duo timber detector

Sylvatest-Duo使超声波沿着着木材的纵向方向传播，用来检测木材的力学性能。根据仪器使用手册进行纵向传播速度的间接测量(见图3)，根据这种测试方法得到的动弹性模量称为间接动弹性模量。这种测量方法可对正在使用的木构件进行检测，可直接应用于现场检测，不需对古建筑进行落架、拆卸。将两个换能器置于试件两端，并同时压紧，每个试件采用“十”字型取点方式进行测试，每个方向重复测试两次，计算其动弹性模量。

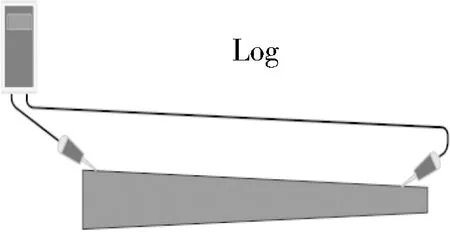
图3 超声波间接纵向测量示意图(图片来源：仪器使用手册)Figure 3 Illustration of indirect longitudinal ultrasonic wave measurement

1.2.2 物理力学性能测试

从已经完成超声波检测的原木心材区截取相应尺寸的无疵小试样试件进行物理力学性能试验，每种实验的测试试件取3个，试验结果取其平均值。

① 密度测试。

按照《木材密度测定方法》(GB1933-2009)对木材密度进行测定。密度计算公式为：

(2)

式中：m为试件的质量；V为试件的体积。

② 抗压强度测试。

按照《木材顺纹抗压强度试验方法》(GB/T 1935-2009)，利用WDW-50E电子式万能试验机对顺纹抗压强度进行测试。沿木材顺纹方向采用均匀速度进行加载，在1～2 min内使试件破坏。抗压强度计算公式为：

(3)

式中：Pmax为破坏荷载；b为试件宽度；t为试件厚度。

③ 抗拉强度测试。

按照《木材顺纹抗拉强度试验方法》(GBT 1938-2009)，利用WDW-50E电子式万能试验机对抗拉强度进行测试。将试件垂直地安装在试验机上，两端固定于钳口中，采用均匀速度进行加载。抗拉强度计算公式为：

(4)

式中：Pu为破坏荷载；A为试件有效部分的截面面积，按A=b·t计算；b为试件有效宽度；t为试件有效厚度。

④ 抗弯强度测试。

按照《木材抗弯强度试验方法》(GB/T 1936.1-2009)，利用WDW-50E电子式万能试验机对抗拉强度进行测试。采用中央加载，将试件放置在试验装置的两支座上，在支座中间试样中部的径面以均匀速度进行加载，在1～2 min内使试件破坏。抗弯强度计算公式为：

(5)

式中：Pmax为破坏荷载；l为试件长度；b为试件宽度；t为试件厚度。

⑤ 顺纹抗压弹性模量测试。

按照《木结构试验方法标准》(GB/T 50329-2012)中附录E：木材顺纹受压应力-应变曲线测定法进行试验，利用WAW-600-G万能试验机对杉木抗压弹性模量进行测定。试件尺寸为75 mm×75 mm×380 mm，其中顺纹方向的长度为380 mm。对短柱进行轴心加载，实验时应保证木材轴心受压，以均匀速度进行加载。抗压弹性模量计算公式为：

(6)

式中：l0为测量变形的标距，本实验为200 mm；ΔF为荷载增量；A为试件截面的面积；Δl0为在荷载增量作用下的压缩变形。

2 结果与分析

2.1 试验测试结果

超声波测试方法获得的间接动态弹性模量、实验室方法获得的木材密度和力学试验机获得的力学性能测试结果见表1。由力学试验机获得的静态抗压弹性模量平均值8341.24 MPa，由超声波法得到的动弹性模量平均值10162.09 MPa，比静弹性模量高21.8%。这一结论与以往的研究结果一致[13]。

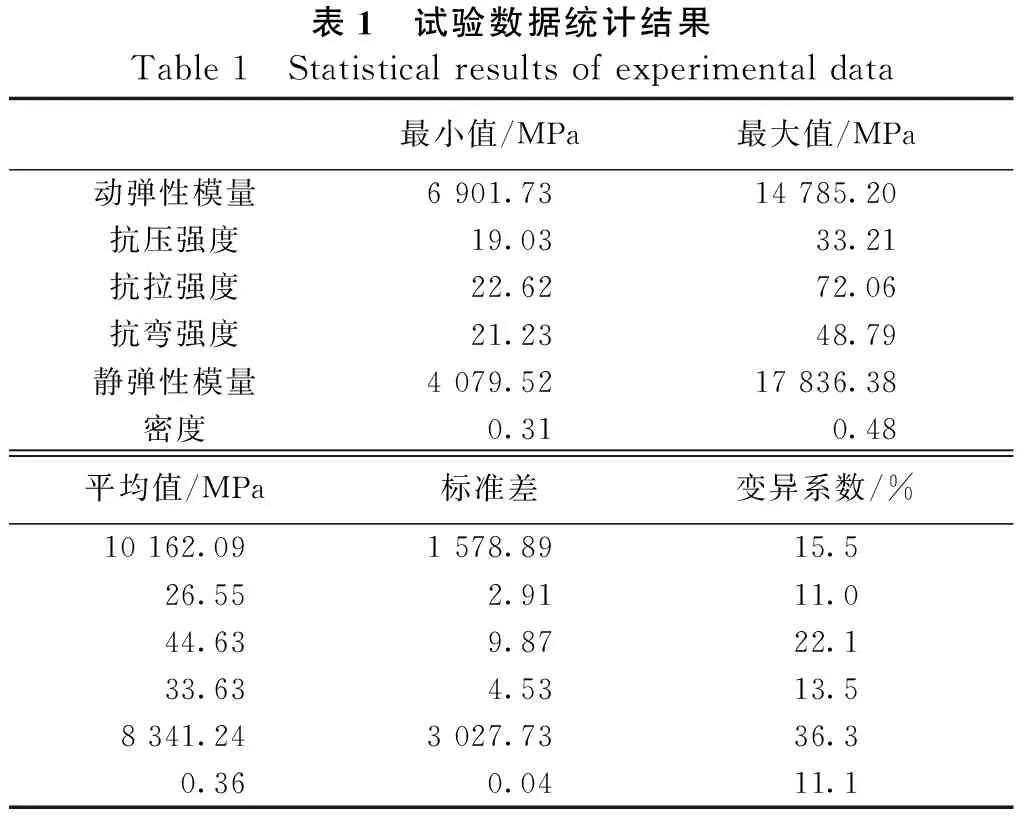
表1 试验数据统计结果Table1 Statisticalresultsofexperimentaldata最小值/MPa最大值/MPa动弹性模量6901.7314785.20抗压强度19.0333.21抗拉强度22.6272.06抗弯强度21.2348.79静弹性模量4079.5217836.38密度0.310.48平均值/MPa标准差变异系数/%10162.091578.8915.526.552.9111.044.639.8722.133.634.5313.58341.243027.7336.30.360.0411.1

2.2 密度与力学性能的关系

木材密度是表征木材性质的一个重要指标，研究表明，大量树种的木材密度与力学性能之间存在一定的相关性。本次试验中杉木密度(ρ)与抗压强度(σc)、抗拉强度(ft)、抗弯强度(σb)、抗压弹性模量(Ec)的关系如图4～图7。采用一元线性回归方程进行分析，得到的数学模型与决定系数见表2。

从图4～图7和表2可以看出：杉木密度和力学性能之间有着一定的线性相关性，其决定系数在0.5左右，杉木密度与抗压强度的相关性最高，决定系数是0.558 8；密度和抗弯强度的相关性次之，决定系数是0.504 1；密度和抗拉强度、抗压弹性模量的相关性相对较低，决定系数分别是0.428 6和0.438 2。

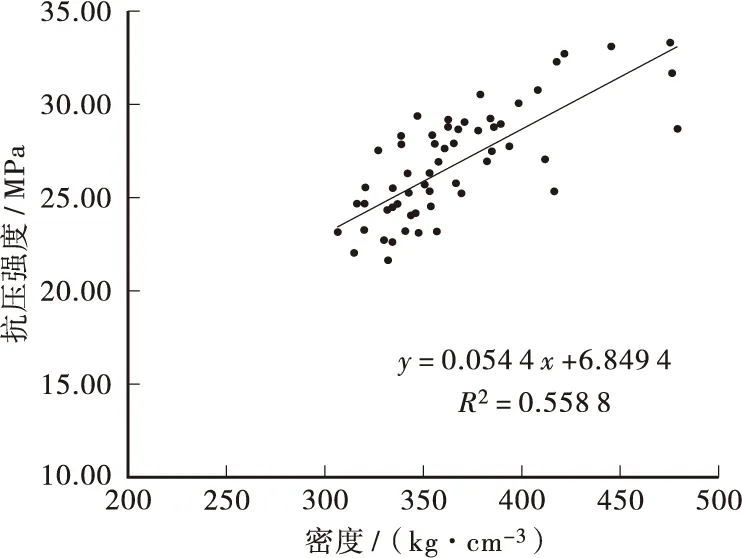
图4 杉木抗压强度与密度的关系Figure 4 Relationship between density and compressive strength

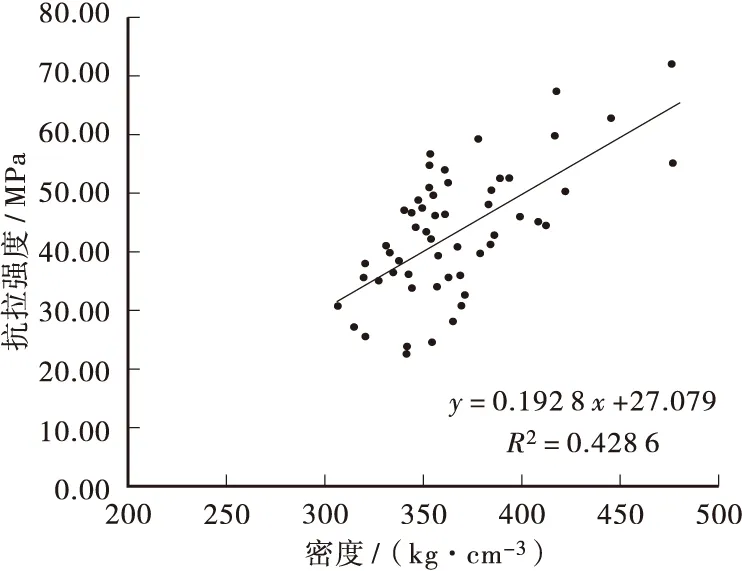
图5 杉木抗拉强度与密度的关系Figure 5 Relationship between density and tension strength

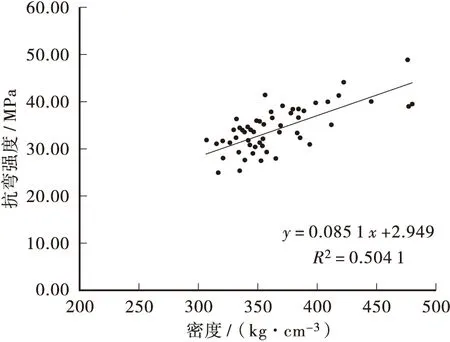
图6 杉木抗弯强度与密度的关系Figure 6 Relationship between density and flexure strength

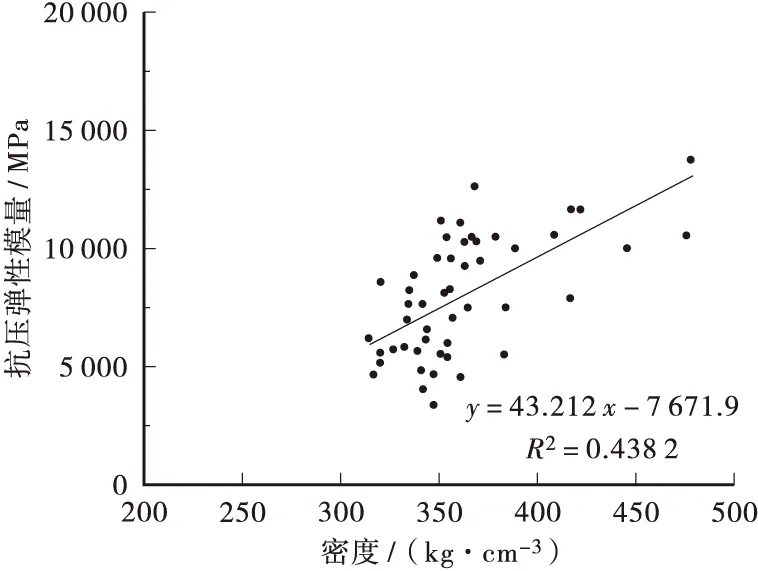
图7 杉木静弹性模量与密度的关系Figure 7 Relationship between density and compressive modulus of elasticity

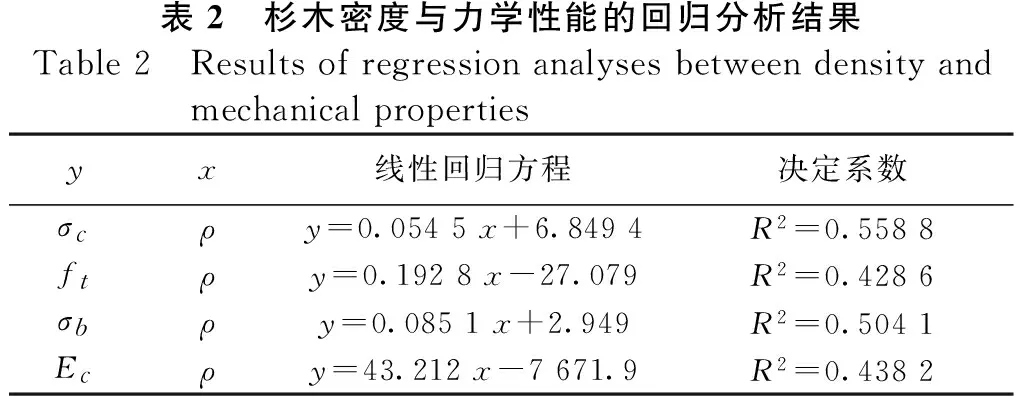
表2 杉木密度与力学性能的回归分析结果Table2 Resultsofregressionanalysesbetweendensityandmechanicalpropertiesyx线性回归方程决定系数σcρy=0.0545x+6.8494R2=0.5588ftρy=0.1928x-27.079R2=0.4286σbρy=0.0851x+2.949R2=0.5041Ecρy=43.212x-7671.9R2=0.4382

2.3 动态弹性模量与力学性能的关系

采用超声波法检测杉木的间接动态弹性模量(Eus)与抗压强度(σc)、抗拉强度(ft)、抗弯强度(σb)、抗压弹性模量(Ec)的关系如图8～图11。采用一元线性回归方程对参数进行分析，得到的数学模型与决定系数见表3。

从图8～图11和表3可以看出：超声波动弹性模量和杉木力学性能之间有着显著的线性相关性，其决定系数甚至到0.6以上，动弹性模量抗压弹性模量与静态抗压弹性模量的相关性最高，决定系数是0.655 2；动弹性模量和抗压强度的相关性次之，决定系数是0.638 5；动弹性模量和抗拉强度、抗弯强度的相关性相对较低，决定系数分别是0.594 6和0.580 9。

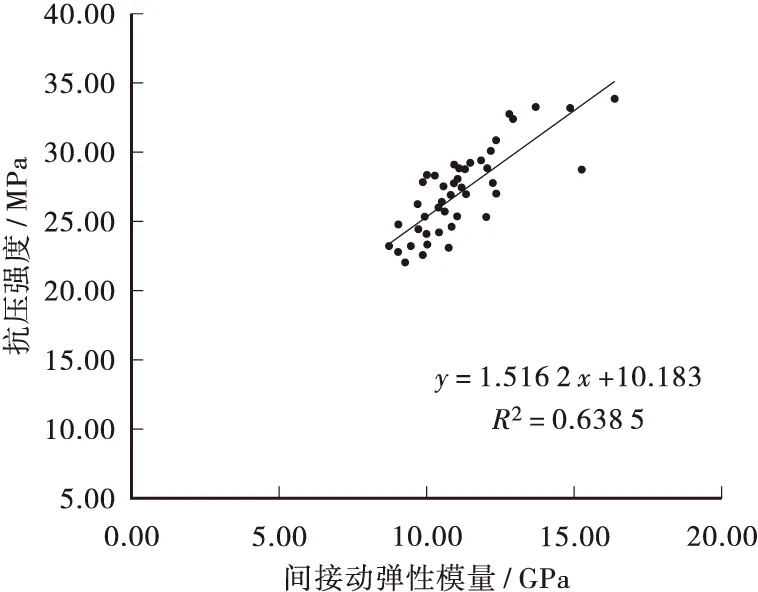
图8 杉木抗压强度与动弹性模量的关系Figure 8 Relationship between dynamic modulus of elasticity and compressive strength

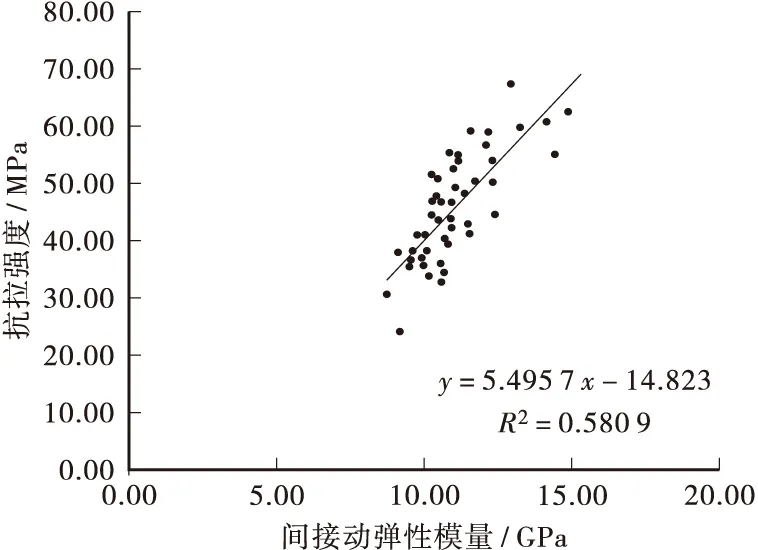
图9 杉木抗拉强度与动弹性模量的关系Figure 9 Relationship between dynamic modulus of elasticity and tensile strength

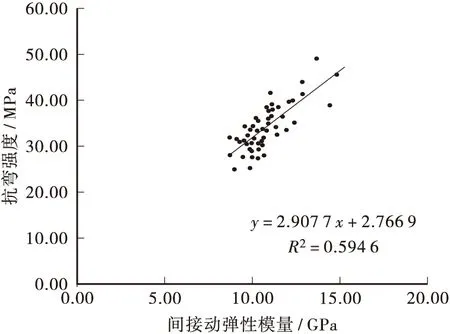
图10 杉木抗弯强度与动弹性模量的关系Figure 10 Relationship between dynamic modulus of elasticity and flexure strength

图11 杉木静弹性模量与动弹性模量的关系Figure 11 Relationship between dynamic modulus of elasticity and compressive modulus of elasticity

表3 超声波间接动弹性模量与力学性能的回归分析结果Table3 Resultsofregressionanalysesbetweendynamicmod-ulusofelasticityandmechanicalpropertiesyx线性回归方程决定系数σcEusy=1.5162x+10.183R2=0.6385ftEusy=5.4957x-14.823R2=0.5809σbEusy=2.9077x+2.7669R2=0.5946EcEusy=1.2995x-4.6846R2=0.6552

3 结论与展望

① 超声波法获得的间接动弹性模量比静态弹性模量高21.8%，两者具有显著的相关性，其决定系数是0.655 2，因此，采用超声波能够有效的检测木材的弹性模量。

② 杉木密度与抗压强度、抗拉强度、抗弯强度、抗压弹性模量之间存在一定的线性关系，决定系数在0.4～0.55。其中，密度与抗压强度的相关性最高，抗弯强度次之，与抗拉强度、抗压弹性模量的相对性较低。

③ 超声波间接动弹性模量与抗压强度、抗拉强度、抗弯强度、抗压弹性模量之间存在显著的线性关系，决定系数在0.6左右，表明，间接动弹性模量与力学性能的相关性高于密度与力学性能的相关性，因此，利用动弹性模量评估构件的力学性能效果更好。其中，间接动弹性模量与抗压弹性模量的相关性最高，抗压强度次之，与抗拉强度、抗弯强度的相对性较低。

④ 超声波间接动弹性模量可以很好地评估木材的力学性能，并且可用于木结构现场检测，不需对木构件进行拆卸，本文为木结构超声波现场检测提供了一定的理论依据。

[1] 黄建中，李雪红，申世杰.浅析我国木材工业的可持续发展[J].林产工业，2008，35(2)：47-48.

[2] 段新芳，李玉栋.无损检测技术在木材保护中的应用[J].木材工业，2002，16(5)：14-16.

[3] 梁善庆，蔡智勇，王喜平，等.北美木材无损检测技术的研究与应用[J].木材工业，2008，22(3)：5-8.

[4] 刘妍，张厚江.木质材料力学性能无损检测方法的研究现状与趋势[J].森林工程，2010，26(4)：46-49.

[5] Almir Sales.Relationship between Density and Ultrasonic Velocity in Brazilian Tropical Woods[J].Bioresource Technology，2006，97(18)：2443-2446.

[6] Almir Sales.Evaluation of the Mechanical Properties of Brazilian Lumber(Goupia glabra)by Nondestructive Techniques[J].Construction and Building Materials，2011，25(3)：1450-1454.

[7] José Saporiti Machado.Non-destructive Evaluation of the Bending Behaviour of In-service Pine Timber Structural Elements[J].Materials and Structures，2011，44(5)：901-910.

[8] Abel Vega.Modelling of The Mechanical Properties of Castanea Sativa Mill.Structural Timber by a Combination of Non-destructive Variables and Visual Grading Parameters[J].European Journal of Wood and Wood Products，2012，70(6)：839-844.

[9] 罗彬.三种无损检测方法评估巨尾桉木材抗弯和抗压强度性质[J].北京林业大学学报，2008，30(6)：137-140.

[10] 张训亚，殷亚芳.两种无损检测法评估人工林杉木抗弯性质[J].建筑材料学报，2010，13(6)：836-840.

[11] 张训亚.超声波预测落叶松规格材的抗弯性能[J].木材工业，2010，24(3)：1-3.

[12] 齐永峰，徐华东，王立海.四种方法测木质材料动弹性模量的对比研究[J].森林工程，2011，27(1)：19-22.

[13] 稽伟兵，马灵飞.利用超声波检测杉木抗弯弹性模量[J].浙江林业科技，2006，26(3)：21-24.

Evaluating Mechanical Properties of Chinese-fir with Ultrasonic Nondestructive Testing

ZHANG Tian， CHENG Xiaowu， LU Weidong， LIU Weiqing

(College of Civil Engineering， Nanjing Tech University， Nanjing， Jiangsu 211816， China)

Mechanical properties is an important indicator of timber，the objective of this study is to investigate the feasibility of ultrasonic nondestructive methods for evaluating mechanical properties.Using a laboratory method to testing density of Chinese-fir logs，To get compressive strength parallel to grain(σc)，tension strength(ft)，flexure strength(σb)，compressive modulus of elasticity(Ec)also using conventional mechanical testing machine for testing.Dynamic modulus of elasticity(Eus)was measured by ultrasonic method.The differences between dynamic modulus of elasticity and static modulus of elasticity is analyzed，the Relationship between density and Mechanical properties，between dynamic modulus of elasticity and mechanical properties were also studied.The analysis results show that： ①dynamic modulus of elasticity(Eus)is slightly larger than the static modulus of elasticity. ②compressive strength parallel to grain(σc)，tension strength(ft)，flexure strength(σb)，static modulus of elasticity(Ec)are somewhat relative with density(ρ). ③compressive strength parallel to grain(σc)，tensile strength(ft)，flexural strength(σb)，static modulus of elasticity and dynamic modulus of elasticity also have some correlation，the relevance is higher than the former.

chinese-fir； ultrasonic； dynamic modulus of elasticity； mechanical properties

2015 — 04 — 20

国家木结构现场检测规范技术规程(71330001)

张 甜(1989 — )，女，山西运城人，硕士，主要从事木结构试验与研究。

S 781.2

A

1674 — 0610(2016)05 — 0066 — 06