基于粗糙集理论的AC-16级配抗滑设计的关键粒组

赵大勇, 童申家

(1.西安建筑科技大学 土木工程学院， 陕西 西安 710055; 2.中铁上海设计院集团有限公司， 上海 200070)



基于粗糙集理论的AC-16级配抗滑设计的关键粒组

赵大勇1,2, 童申家1

(1.西安建筑科技大学 土木工程学院， 陕西 西安 710055; 2.中铁上海设计院集团有限公司， 上海 200070)

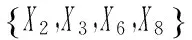
道路工程； 沥青混凝土； 抗滑； 分形； 灰色关联分析； 粗糙集

0 引言

路面抗滑性能是影响行车安全的主要因素之一，其好坏与路面纹理特征密切相关[1]。路面纹理分布特征可用路面纹理分形维数DZ来描述[2-4]，通过建立DZ与摆值和构造深度的相关关系，可给出用以评价沥青路面抗滑性能的DZ值。有研究表明：在材料相同的条件下，矿料级配组成对沥青路面抗滑指标的影响很大[5,6]。由分形级配理论可知，对于连续级配沥青混合料，其级配组成特征可用粒径分布分形维数D来表征[7]，不同级配的沥青混合料，对应不同的粒径分布分形维数D。因此，如何建立路面纹理分形维数DZ与集料粒径分布分形维数D的关系，并按分形级配理论调整矿料级配曲线，提供了沥青混凝土路面抗滑级配设计的新思路。本文拟从沥青混合料分形结构出发，通过建立路面纹理分形维数DZ与沥青混合料级配特征之间的联系，推导路面纹理分形维数DZ的计算公式，并按照灰色关联分析法，对粒组集料含量与路面纹理分形维数DZ之间的关联程度进行分析，根据关联度的大小对粒组进行分类；同时借助粗糙集理论的属性约简功能，对不同类别粒组进行约简，从而提出AC — 16沥青混凝土路面抗滑级配设计的关键粒组。

1 路面纹理分形维数与粒径分布分形维数的关系

1.1 沥青混合料的分形结构

沥青混合料是由沥青、集料、矿粉组成的复合材料体系，具有显著的分形特征，存在着以下几个层次的分形： ①不同粒径的集料混合形成一种分布，其分布函数是一种数学分形，称为集料粒径分布分形； ②因集料粒径分布分形导致集料质量分布函数的分形，称为集料级配分形； ③沥青混合料存在空隙，集料无法填满整个空间，这种空间填充能力不足形成体积分形[8，9]。

1.2 沥青混合料集料粒径分布分形维数

杨瑞华等[9，10]根据分形几何基本原理，推导了连续级配沥青混合料集料粒径分布的分形模型：

(1)

式中： m(r)为粒径不大于r的集料质量；m0为集料总质量；P(r)为各粒径集料的筛孔通过率；D为集料粒径分布分形维数；rmin为集料最小粒径；rmax为集料最大粒径。

在连续级配中rmin远小于rmax，故rmin可以忽略，从而(1)式可写为:

P(r)=(r/rmax)3-D

(2)

对式(2)两边同取对数可得：

lgP(r)=(3-D)lg(r/rmax)

(3)

由式(3)可知：lgP(r)与lg(r/rmax)具有线性相关性，因此在双对数坐标图中，对级配曲线进行拟合，根据拟合直线斜率k=3-D即可算得D值。

1.3 沥青路面纹理分形维数

在讨论沥青路面纹理分形维数之前，先给出分形几何基本公式：

A(δ)=A0(δ/δmax)E-D

(4)

式中：A0为图形是整形时A的数值；δ为度量码尺；δmax为最大码尺长度；D为分形维数；E=0时，A和δ对应于点数；E=1时，A和δ对应于长度；E=2时，A和δ对应于面积；E=3时，A和δ对应于体积。

由(4)式可给出沥青混合料集料体积分形和路面纹理分形如下：

V(r)=V0(r/rmax)3-DV

(5)

Z(r)=Z0(r/rmax)1-DZ

(6)

式中：V(r)为分形体积；V0为整形体积；DV为体积分形维数；Z(r)为路面纹理分形；Z0为整形路面纹理；DZ为路面纹理分形维数。

集料空间填充能力不足形成体积分形，路面纹理分形可看作集料填充能力不足在路面纵横向的反映，故集料体积分形与路面纹理分形存在一阶导数关系，即：

Z(r)=dV(r)/dr

(7)

若以ρ(r)表示粒径不大于r的集料平均密度，则：

(8)

为使问题简化，忽略不同粒径集料密度ρ(r)的差异，则：

(9)

将式(2)代入式(9)并结合式(7)可得：

(10)

对比式(6)和式(10)可知：

DZ=D-1

(11)

式(11)建立了路面纹理分形维数DZ与集料粒径分布分形维数D之间的关系。对于连续级配沥青混合料而言，其级配特征可用粒径分布分形维数D来描述，不同级配的沥青混合料，对应不同的粒径分布分形维数D。式(11)实质在路面抗滑性能与沥青混合料级配特征之间建立了联系，这提供了路面抗滑级配设计的新思路。

2 基于灰色关联分析的粒组分类

2.1 试验级配

本论文采用集料最大粒径为19 mm的AC — 16级配，按规范推荐的级配曲线范围确定的10组集料级配见表1。其中级配1～5为代表性级配走向： 1接近规范上限，2接近下限，3接近中值，4沿0.075～16 mm筛孔，级配曲线由上限到下限，5沿0.075～16 mm筛孔，级配曲线由下限到上限，涵盖了级配曲线范围所有可能的级配走向；级配6～10为在级配曲线范围内随机选取级配。

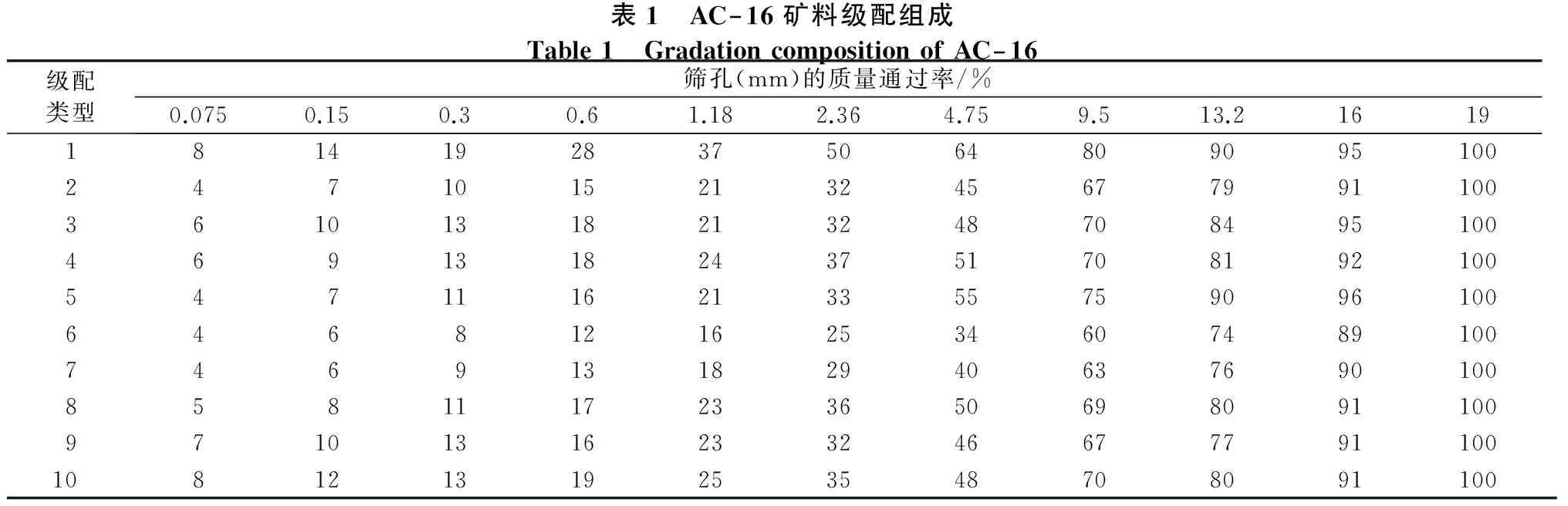
表1 AC—16矿料级配组成Table1 GradationcompositionofAC—16级配类型筛孔(mm)的质量通过率/%0.0750.150.30.61.182.364.759.513.216191814192837506480909510024710152132456779911003610131821324870849510046913182437517081921005471116213355759096100646812162534607489100746913182940637690100858111723365069809110097101316233246677791100108121319253548708091100

2.2 路面纹理分形维数计算

以级配1为例来说明路面纹理分形维数DZ的计算过程。将级配1的级配曲线绘于双对数坐标系中并进行线性拟合，见图1，由拟合直线斜率k=3-D，得集料粒径分维数D=2.5610，由式(11)可得路面纹理分形维数DZ=1.5610，按相同方法可计算其它级配类型的路面纹理分形维数，计算结果见表2。

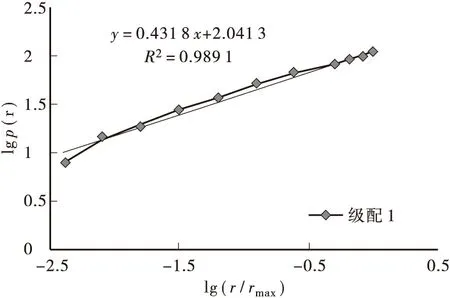
图1 级配双对数图Figure 1 Double logarithmic figure of gradation

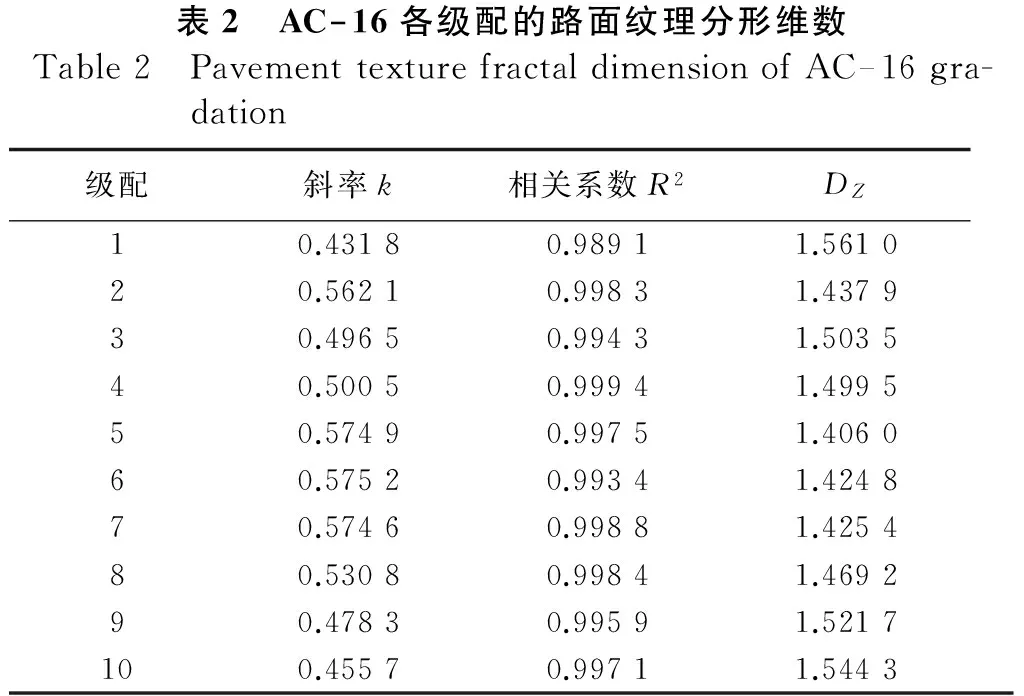
表2 AC—16各级配的路面纹理分形维数Table2 PavementtexturefractaldimensionofAC—16gra-dation级配斜率k相关系数R2DZ10.43180.98911.561020.56210.99831.437930.49650.99431.503540.50050.99941.499550.57490.99751.406060.57520.99341.424870.57460.99881.425480.53080.99841.469290.47830.99591.5217100.45570.99711.5443

2.3 路面纹理分形维数与粒组含量灰色关联分析

2.3.1 灰色关联分析模型的建立

选取各粒组集料含量为比较序列变量Xi(k)，路面纹理分形维数为参考序列变量X0(k)，假设X0(k)=f(Xi(k))，则变量Xi(k)与变量X0(k)按映射f相关联。

2.3.2 依据模型计算灰色关联度

由比较序列及参考序列形成灰色关联分析原始数据表，见表3。表中各粒组集料含量X1(≤0.075)、X2(0.075～0.15)、X3(0.15～0.3)、X4(0.3～0.6)、X5(0.6～1.18)、X6(1.18～2.36)、X7(2.36～4.75)、X8(4.75～9.5)、X9(9.5～13.2)、X10(13.2～16)、X11(16～19)共十一个粒组，构成比较序列指标；路面纹理分形维数X0，构成参考序列指标。

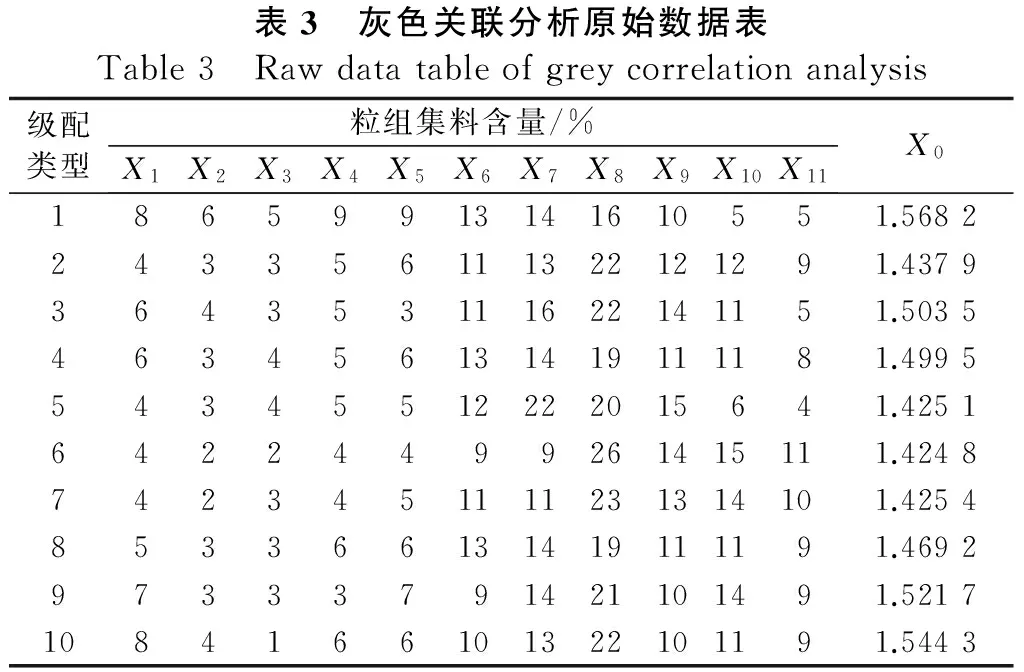
表3 灰色关联分析原始数据表Table3 Rawdatatableofgreycorrelationanalysis级配类型粒组集料含量/%X1X2X3X4X5X6X7X8X9X10X11X018659913141610551.5682243356111322121291.4379364353111622141151.5035463456131419111181.499554345512222015641.425164224499261415111.42487423451111231314101.4254853366131419111191.469297333791421101491.52171084166101322101191.5443

灰色关联度的计算步骤如下：

③ 根据公式ξi(k)=Δmin+ρΔmax/Δi(k)+ρΔmax，计算粒组含量与路面纹理分形维数之间的关联系数，式中ρ为分辨系数，依据文献[11-14]关于分辨系数的研究，取ρ=0.5。

表4 粒组含量与路面纹理分形维数的关联度Table4 Correlationdegreebetweentexturefractaldimensionandgraingroupγ1γ2γ3γ4γ5γ6γ7γ8γ9γ10γ110.8210.7280.7870.7540.7680.9280.8900.7600.8000.5110.663

2.3.3 依据关联度的粒组分类

当取ρ=0.5时：若γi≥0.6，则子母因素有关联；γi<0.6时，则关联性较差；γi<0.5时认为无关联[7,12]。由表4的关联度分析结果可知：γ10=0.511，即粒组X10(13.2-16)与路面纹理分形维数的关联性较差，其对路面纹理分形维数的影响可以忽略；其余γi均大于0.6，即粒组X1、X2、X3、X4、X5、X6、X7、X8、X9、X11与路面纹理分形维数存在关联，但不同粒组与路面纹理分形维数之间的关联程度并不相同，其中γ6=0.928为最大，即粒组X6(1.18-2.36)对路面纹理分形维数的影响程度最大，γ11=0.663为最小，即粒组X11(16-19)对路面纹理分形维数的影响程度最小。根据灰色关联度的大小，可将粒组分为四个粒组类别，见表5。

表5 粒组类别表Table5 Categoriesofgraingroup类别粒组关联度类别粒组关联度一X110.663X20.728X40.754二X80.760X50.768X30.787三X90.800X10.821四X70.890X60.928

同一粒组类别中的各粒组与路面纹理分形维数的关联度相差不大，即其对路面纹理分形维数的影响程度基本相当，以哪一粒组作为决定路面纹理分形维数的关键粒组，很难做出取舍。粗糙集理论具有属性约简功能，能在灰色关联分析的基础上，进一步将影响因素归一划分[7]，约简数据库中的冗余属性，简化知识表达，方便用户决策。

3 基于粗糙集理论的粒组约简

3.1 粗糙集理论基本概念

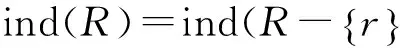
定义4： 若存在独立的Q=P-r，Q⊆P，满足ind(Q)=ind(P)，则称Q为P的一个约简，用red(P)表示，通常P有多种约简，全部约简的交集定义为P的核，记作core(P)=∩red(P)。

3.2 粒组含量与路面纹理分形维数预测决策表的建立

3.3 基于粗糙集理论的属性约简

本文以基于粗糙集理论的表格逻辑数据分析工具Rosetta为计算平台，采用基于遗传算法的粗糙集属性约简改进算法对决策信息表的条件属性进行约简，条件属性的6种约简结果见表7。

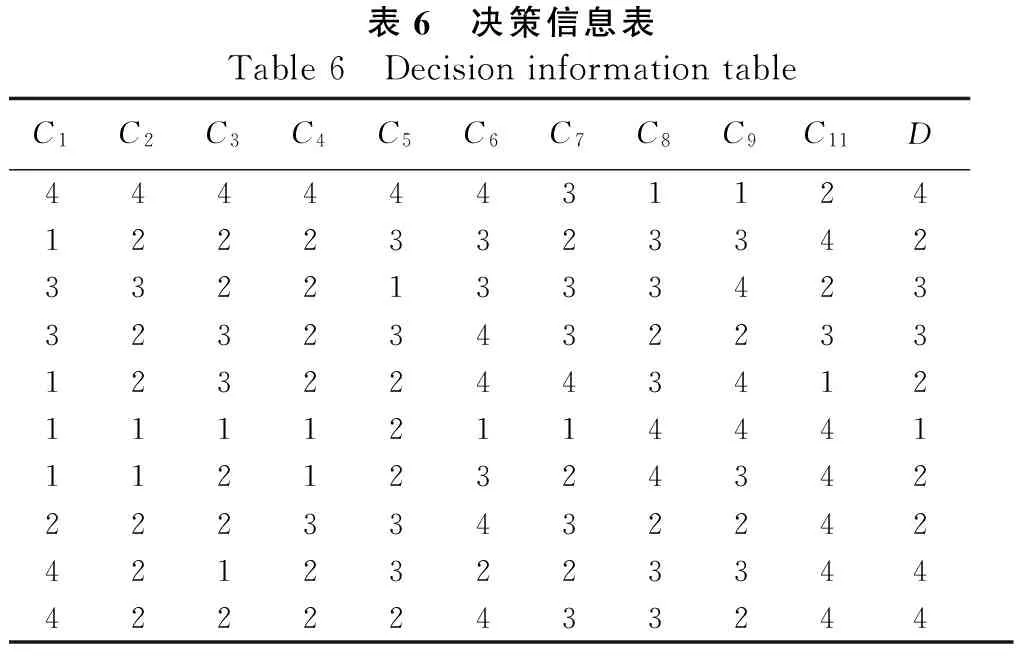
表6 决策信息表Table6 DecisioninformationtableC1C2C3C4C5C6C7C8C9C11D44444431124122233233423322133342332323432233123224434121111211444111212324342222334322424212322334442222433244

表7 条件属性的约简结果Table7 Reductionresultsofconditionattribution编号约简冗余属性1C3,C5,C7{}C1,C2,C4,C6,C8,C9,C11,2C3,C5,C6{}C1,C2,C4,C7,C8,C9,C113C3,C8,C9{}C1,C2,C4,C5,C6,C7,C114C3,C4,C6,C7{}C1,C2,C5,C8,C9,C115C3,C7,C8,C11{}C1,C2,C4,C5,C6,C96C2,C3,C6,C8{}C1,C4,C5,C7,C9,C11

3.4 约简结果分析

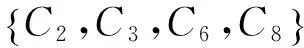
4 结语

① 从沥青混合料的分形结构出发，建立了路面纹理分形维数DZ与集料粒径分布分形维数D之间的关系，推导了DZ的计算公式，给出了DZ的计算方法，在沥青混合料级配特征与路面抗滑性能之间建立了联系，提供路面抗滑级配设计的新思路。

② 运用灰色关联分析方法，对粒组集料含量与路面纹理分形维数的关联性进行了研究，根据灰色关联度的大小，将粒组分为四个粒组类别，同一粒组类别中的各粒组与路面纹理分形维数的关联度相差不大，其对路面纹理分形维数的影响程度基本相当。

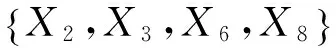
[1] Gendy A E, Shalabby A. Mean profile depth of pavement surface macro-texture using photometric stereo techniques[J]. Journal of Transportation Engineering,2007,133(7):433-440.

[2] 黄宝涛,田伟平,李家春,等.沥青路面抗滑性能定量评价的分形方法[J].中国公路学报,2008,21(4):12-17.

[3] 张令刚，钱振东，杨理广，等. 沥青混凝土路面表面形貌及抗滑性能的分形表达研究[J]. 公路,2013(5):85-88.

[4] 王维锋, 严新平, 初秀民，等. 基于分形理论的沥青路面微观形貌特征描述和求解方法[J]. 吉林大学学报:工学版, 2010, 40(6): 1538-1542.

[5] 张宜洛. 抗滑级配类型沥青混合料的抗滑性能[J]. 长安大学学报:自然科学版,2003,23(1):7-10.

[6] 赵战利, 张争奇, 胡长顺. 集料级配对沥青路面抗滑性能的影响[J].长安大学学报:自然科学版,2005,25(1):6-9.

[7] 赵大勇,张建国.基于灰色关联分析的密级配沥青混合料分形维数研究[J].兰州交通大学学报,2014,33(4):66-71.

[8] 李国强, 邓学均. 级配骨料的分形效应[J]. 混凝土,1995(1):3-7.

[9] 杨瑞华, 许志鸿. 密级配沥青混合料集料分形分维与路用性能的关系[J]. 土木工程学报, 2007, 40(3): 98-103, 109.

[10] 杨瑞华,许志鸿,张 超,等.沥青混合料分形级配理论[J].同济大学学报:自然科学版,2008,36(12):1642-1646.

[11] 吕峰. 灰色系统关联度之分辨系数的研究[J]. 系统工程理论与实践, 1997(6): 49-54.

[12] 郭洪. 灰色系统关联度的分辨系数[J]. 模糊数学, 1985(2): 55-58.

[13] 范凯,吴皓莹.灰色系统关联度中一种新的分辨系数确定方法[J].武汉理工大学学报,2002,24 (7) :87-89.

[14] 刘思峰，郭天榜. 灰色系统理论及其应用[M].北京:科学出版社, 2000.

The Key Grain Group for Anti-sliding Gradation Design of AC-16 Based on Rough Set Theory

ZHAO Dayong1,2, TONG Shenjia1

(1.School of Civil Engineering,Xi’an University of Architecture and Technology,Xi’an Shanxi 710055, China; 2.China Railway Shanghai Design Institute Group Co.Ltd, Shanghai 200070, China)

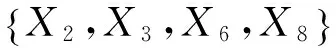
road engineering; asphalt concrete; skid-resistance performance; fractal; grey correlation analysis; rough set

2015 — 04 — 20

国家自然科学基金青年科学基金项目(51408480)；西部交通建设科技项目(20113187721260)

赵大勇(1987 — )，男，甘肃平凉人，硕士生，主要从事公路工程等方面的研究。

U 414.1

A

1674 — 0610(2016)05 — 0017 — 05