分类数据的多目标模糊中心点聚类算法
周治平 朱书伟 张道文
(江南大学物联网工程学院 江苏无锡 214122) (zzp@jiangnan.edu.cn)
分类数据的多目标模糊中心点聚类算法
周治平 朱书伟 张道文
(江南大学物联网工程学院 江苏无锡 214122) (zzp@jiangnan.edu.cn)
针对传统面向分类属性数据的聚类算法大多是对单一指标优化而存在的局限性,将类内和类间信息同时引入到优化过程中,结合多目标优化算法与模糊中心点聚类,提出一种新颖的多目标模糊聚类算法.与传统的基于遗传算法的混合聚类方法不同的是,采用模糊隶属度对染色体进行编码,同时优化2个相对的聚类目标函数获得一组最优解集,并且采用了一种提前终止准则判断算法是否达到稳定状态并停止操作,以减少不必要的计算开销.为了进一步提高算法的效率,通过采样子集计算出相应的模糊中心点作为类的表达,然后以这些模糊中心点计算出全体样本的隶属度矩阵即可获得最终的聚类结果.对10种数据集的实验结果表明:所提方法在聚类精度和稳定性方面优于当前最新的多目标聚类算法,且计算效率也获得较大的提升.
分类数据;聚类;多目标优化;模糊中心点;最优解集
聚类分析是一种无监督的数据分析方法,在数据挖掘、模式识别、信息检索等领域应用十分广泛.数据的属性类型通常包括数值属性、分类属性以及混合属性,其中数值型数据可直接采用相应的距离度量探索其几何特性,且现有的大部分聚类算法都是对数值型数据进行分析.然而,对于属性值为离散型的分类数据,无法通过距离度量的方式进行分析,近来关于分类数据聚类算法的研究得到越来越多学者的关注.
最经典的分类数据聚类算法是对K-means原型进行拓展的K-modes(KMd)算法[1]及其模糊版本的fuzzyK-modes(FKMd)算法[2],随后Kim等人[3]针对FKMd中硬中心点的不足,提出基于模糊类中心集的模糊中心点(fuzzy centroids, Fcentroids)的算法.由于K-modes型算法具有处理大数据集的能力,现已成为分析分类数据最广泛的聚类算法.然而,K-modes中采用简单匹配相异性度量无法有效区分不同的属性值,一些更有效的相异性度量方式[4-7]相继被提出.为了能够有效避免局部最优,Gan等人[8]提出基于遗传算法的GA-FKM(genetic algorithm fuzzyK-modes);Maulik等人[9]结合改进的差分进化算法与模糊c中心点(c-medoids)算法提出一种新颖的混合聚类算法.考虑到聚类过程中不同属性的重要性不同,Chan等人[10]提出一种属性加权聚类算法.Bai等人[11]对其进行拓展,提出一种混合属性加权聚类算法,能够有效地用于高维分类数据.近来,他们针对传统K-modes型算法仅考虑簇内信息的不足,引入簇间信息建立了新的目标函数分别提出模糊版本[12]和非模糊版本[13]的新算法.然而,在新的目标函数中对平衡参数的取值仍然难以确定.
通常多目标聚类算法能够有效克服仅对单一指标优化的不足,同时兼顾多个聚类指标且不引入新的参数,自提出以来得到了广泛的研究.Mukhopadhyay等人[14]基于非支配排序遗传算法(nondominated sorting genetic algorithm-Ⅱ, NSGA-Ⅱ)首次提出了面向分类数据的多目标模糊聚类算法,对全局紧密度与模糊分离度2个指标同时优化,具有重要的指导意义.近来,Saha等人[15]采用改进多目标差分进化算法提出了基于增量学习机制的多目标聚类方法;Yang等人[16]基于NSGA-Ⅱ并采用模糊隶属度的染色体编码机制提出新颖的NSGA-FMC(non-dominated sorting genetic algorithm-fuzzy membership chromosome),均能够获得更佳的聚类结果.此外,与多目标聚类提出背景相近的聚类集成技术在分类数据中也得到了一定的关注,如一种基于链接的聚类集成方法[17]、基于粗糙集子空间的聚类集成方法[18]、基于集成的粗糙模糊集聚类算法[19]等.
现有的分类数据多目标聚类算法都是以FKMd为原型,本文以一般情况下准确度更高的Fcentroids为原型提出一种新颖的多目标聚类算法.以最新提出的NSGA-FMC为基础,将NSGA-Ⅱ融入Fcentroids以进一步改善算法的性能.通过与NSGA-FMC及其他5种算法的实验对比分析表明了本文算法在聚类准确度与稳定性方面的优势,并且其对模糊参数的敏感性相对较低,拥有较高的鲁棒性.
1 传统的分类数据聚类算法
1.1 FKMd聚类的概念
模糊聚类是一种软划分的聚类方法,即每个样本未明确规定到某一个类,而是根据一个模糊隶属度值uki(0≤uki≤1)确定某个样本xi属于第k个类的程度.经典的FKMd算法的目标函数为[2]
(1)
其中,m为模糊指数,一般m>1;ck为第k个mode的位置;D(ck,xi)为第i个数据与第k个mode之间的相异性度量,采用简单匹配的度量方法:
(2)
模糊隶属度uki表示了第i个数据隶属于第k个类的程度,其更新过程如式(3)所示[2]:
(3)
此外,若modes中心ck(1≤k≤K)的第j(1≤j≤D)维属性具有t个属性值,则ckj的更新过程为[2]
(4)
通过更新隶属度和modes中心使目标函数F(U,C)的值不断减小直至不再发生明显变化则停止运行,通过U求出每个点的最大隶属度以确定其所属的类别.由于K-modes型的聚类算法是以K-means为原型,同样存在2个主要缺点:1)对初始modes的选取非常敏感;2)容易陷入局部最优解.目前,关于初始modes值选取方面已取得了许多不错的研究成果[20-22].
1.2 Fcentroids聚类的概念
Fcentroids算法是一种基于模糊集理论的聚类方式,其目标函数的形式与式(1)相同,但与传统的硬中心点不同的是,每个centroid的每一维属性采用一个模糊集来表示,若第k个centroid向量为[3]
ck={ck1,ck2,…,ckD}, 1≤k≤K,


(5)
由式(5)可见模糊中心点的每一维属性对应一个集合,不再是一个确定的值,其相异性度量方式也随之改变,定义为式(6):
(6)

(7)
此外,与FKMd不同的是这里不存在数据样本与centroids相等的情况,因此uki的更新过程为[3]
(8)
除了上述内容,Fcentroids的原理与FKMd基本相同,相对于后者其具有很高的稳定性,但是它同样存在陷于局部最优的问题.目前相关的研究相对较少,Ji等人[23-24]分别基于模糊聚类和子空间聚类提出2种面向混合数据的改进K-prototype算法模型,其目标函数中以Fcentroids对分类属性部分进行分析.
2 基于多目标进化算法的模糊中心点聚类
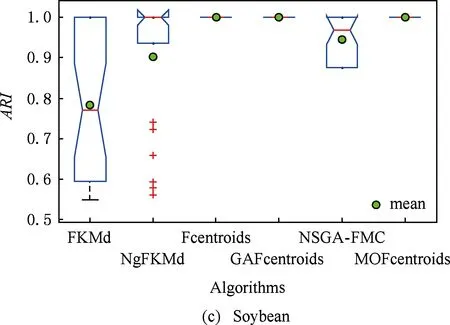
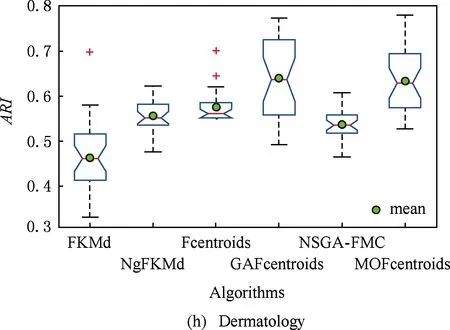
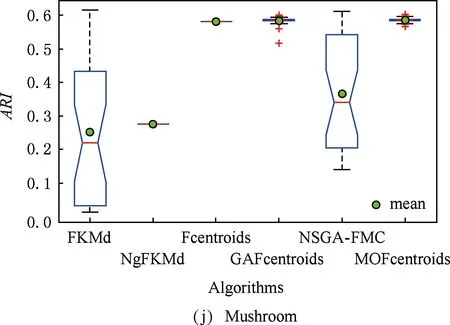
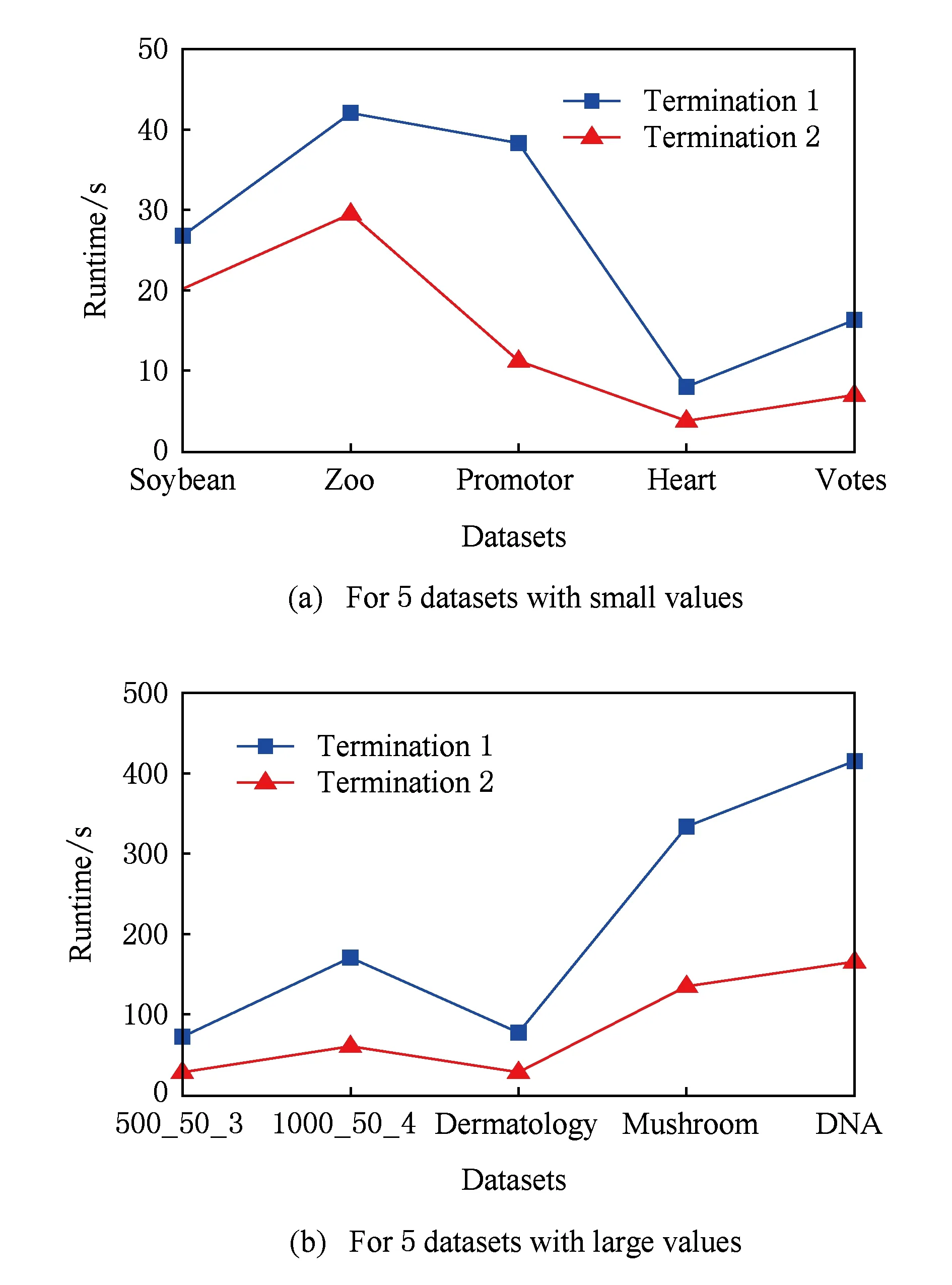
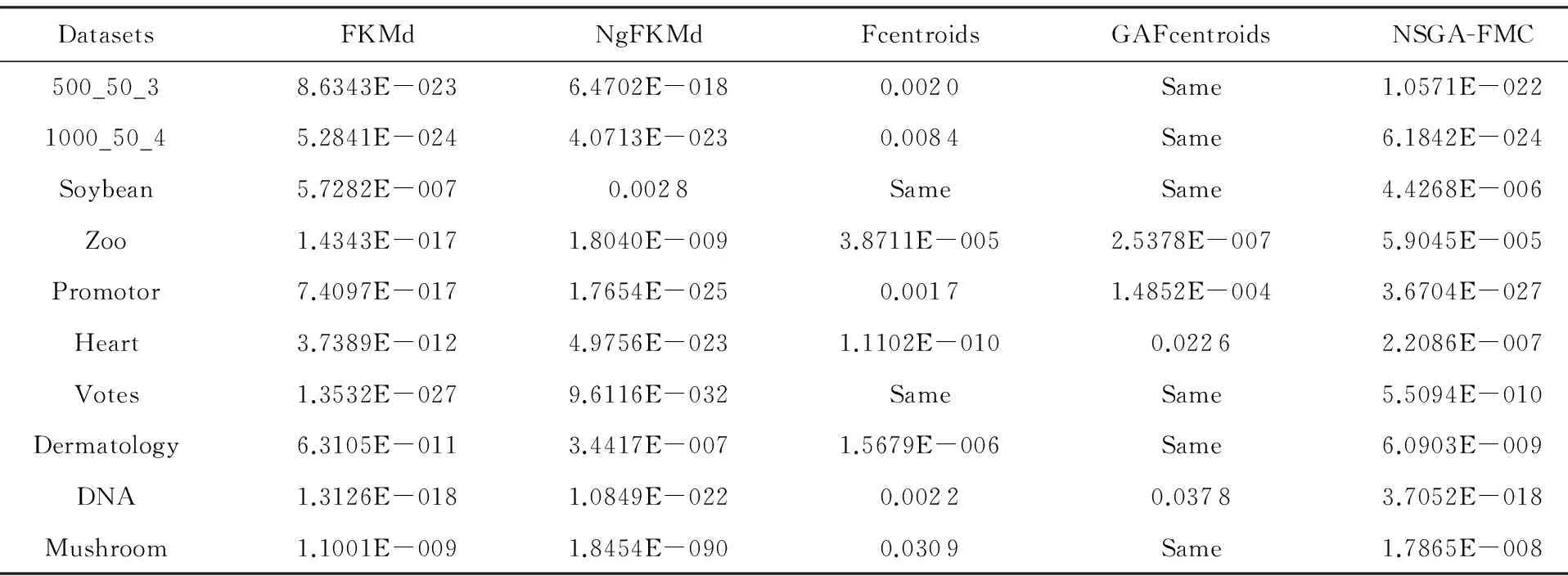
多目标优化问题就是在决策向量空间中,均衡考虑具有对立性的多个指标并获得最优解集.对于最小化问题而言,若2个决策向量分别为xk和xl,当且仅当∀i∈{1,2,…,n}使得解f(xk)≤f(xl),∃j∈{1,2,…,n}使得解f(xk) 2.1 染色体编码 由于MOFcentroids的centroids是由一组模糊集表示的,因此无法直接通过某个特定的属性值代表其某一维属性,即无法像文献[9,14-15,25-27]中那样基于聚类中心对染色体的基因位编码.在文献[8,16]中均采用的是基于模糊隶属度的编码方式,因此本文采用模糊隶属度作为染色体的基因位.每个个体向量表示为x=(u11,u21,…,uK1,u12,u22,…,uK2,…,u1n,u2n,…,uKn),可以看出它是K×n列的行向量,其中K为类数,n为数据的个数,所有数据的隶属度必须满足式(1)中约束条件.通过搜索到最佳的属性权重向量的同时可以获得较优的centroids,并能够得到相应的聚类结果.在计算过程中需将每个染色体向量转化为一个K行n列的矩阵以方便操作,模糊隶属度矩阵为 (9) 2.2 目标函数的选取 多目标聚类算法的性能在很大程度上取决于目标函数的选取,现有文献中大部分选取2个目标函数进行优化并且主要考虑的是划分的紧密性和分离性的性能.本文中MOFcentroids的目标函数并没有采用文献[14,16]的模糊紧密性与模糊分离性,而是选取F(U,C)和XB(Xie-Beni)指数,其中F(U,C)如式(1)所示.XB为结合类内和类间信息的目标函数,在现有的各种类型多目标聚类算法[15,25-27]中已被证明非常有效,它的形式如式(10)所示,其分子部分与F(U,C)相同,分母部分n表示数据的个数,D(ci,ck)为第i个类与第k个类之间的相异度. (10) 对于F(U,C)和XB,本文在计算D(ck,xi)时都采用的是式(6)的方式,但是其中的置信度并没有根据式(7)确定,而是做了适当调整[23-24]: (11) 此外,XB分母中D(ci,ck)的计算为 (12) 2.3 染色体选择 由于Fcentroids是一种相对比较稳定的算法,而NSGA-FMC是以FKMd为基础,本文算法对于某些数据集并不会像NSGA-FMC那样产生包括较多最优解的解集,因此NSGA-FMC中基于轮盘赌的选取方式无法满足要求,这里仍然采用的是二进制锦标赛的选取方式.对所有的父代种群进行非支配排序,其中互不支配的个体通过拥挤度距离判断其优先等级,若第i个染色体的非支配等级ir以及拥挤度距离id,则拥挤性比较算子n可定义为 如果ir inj, (13) 此外,由于在后续的内容中需要采用文献[8,16]中的轮盘赌选取方式,这里主要介绍其中的基于等级的评估函数[8,16]: F(xi)=β(1-β)ir-1, (14) 其中,xi为第i个染色体向量;β∈[0,1]为预定义的常数,用来表明算法的选择强度. 2.4 交叉过程 当所有染色体被选出后,需对其执行交叉操作,与GA-FKM中的一步FKMd相类似,本文算法采用一步Fcentroids作为交叉算子,其过程为 fori=1 toNdo 根据式(9)将xi转化为隶属度矩阵Ut; 利用Ut并通过式(11)计算出矩阵ω即可确定所有的centroids; 利用ω表示的centroids并通过式(8)更新模糊隶属度矩阵表示为Ut+1; 将Ut+1转化为一个行向量获得新的染色体; end for 2.5 变异过程 在变异过程中,每个基因以概率Pmu发生变化: fori=1 toNdo 染色体为xi=(u11,…,uK1,…,u1n,…,uKn); fors=1 tondo 产生一个在[0,1]内的随机数r; ifr 产生K个在[0,1]内随机数v1s,v2s,…vKs; end if end for end for 2.6 停止准则 本文首先设置了最大迭代数作为停止判断标准,需要注意的是虽然Fcentroids设置了最大迭代次数,但大多情况下会由于目标函数值没有明显的降低而提前停止.同样地,当MOFcentroids运行到一定阶段时达到稳定使其PF不会发生明显的变化,若达到最大迭代次数才停止则会增加不必要的计算开销.这里进一步采用了一种对PF进行动态评价的方法,分别计算每次迭代后PF所对应的各目标函数值的最优值,若第t次迭代后分别为Fbest(t)和XBbest(t),则Δπ1=Fbest(t)-Fbest(t+1)和Δπ2=XBbest(t)-XBbest(t+1)分别表示下一次迭代后各个目标函数最优值的变化程度,设定一个很小的阈值ε=10-4,若连续T1次迭代满足Δπ1+Δπ2≤ε则可判断PF已处于稳定状态,算法提前终止,本文将这种方法称为提前终止准则. 2.7 最终解的选取 当多目标聚类算法停止以后,需通过PS确定最终的聚类解,目前使用比较广泛的方法主要有2种:1)通过聚类有效性指标对PS中的每个解进行评估并选取一个最优解获得聚类结果[25-26];2)结合机器学习与聚类集成方法通过综合PS中的所有解以确定最终的聚类结果[14-15,27],目前具有更好的前景但也存在计算开销大的问题.而在NSGA-FMC中提出了一种简单高效的方法,由于其每一个非支配解可转化为相应的模糊隶属度矩阵,通过每个数据对应的最大隶属度值即可确定其所属的类别,将这些隶属度值相加得到隶属度总和,最后比较所有非支配解对应的隶属度总和并选取其中最大的值以确定聚类解.本文算法同样采用的是基于模糊隶属度的编码方式,因此采用这种方法从PS中选取最终解. 2.8 算法具体流程 算法1. MOFcentroids算法. Step1. 初始化当前迭代次数Iter=0,最大迭代次数Tmax、种群规模N、聚类数K、模糊指数m、交叉概率Pc、变异概率Pmu,对于每个染色体从数据集中随机选出K个数据确定初始的ck(1 Step2. 根据初始的置信度ω以及隶属度矩阵U分别计算目标函数F(U,C)和XB,并以n对种群进行非支配排序. Step3. 采用二进制锦标赛机制选出N个染色体分别执行交叉、变异操作得到子代种群. Step4. 对子代种群利用式(11)和式(8)分别更新ω以及U并计算相应的F(U,C)和XB. Step5. 执行精英保留机制,将父代种群与子代种群混合,再次采用n对它们进行非支配排序并从中选出前N个染色体作为下一次迭代的父代种群. Step6. 判断是否满足提前终止准则,若满足则停止并输出最优解集,并转Step8,否则转Step7. Step7.Iter=Iter+1,若Iter Step8. 将每一个非支配解转化为相应的模糊隶属度矩阵,计算最大隶属度总和选出最终的聚类解. 此外,这里为了使初始时ck(1≤k≤K)每一维属性对应的属性值都具有一定的代表性,在Step1中根据随机选出的K个数据确定初始ck的规则如下: (15) 2.9 基于采样选取模糊类中心点 由于多目标聚类算法的计算时间相对较长,除了提前终止准则外,本文采用一种基于采样的技术[28]以进一步提高其计算效率,即聚类前从整体数据集X中随机采样n′个样本X′,并用MOFcentroids计算出最能代表X′的centroids集合Θ′,其原理基于这样的假设:如果采样的X′能够代表X中的数据点的统计分布,Θ′将会很好地逼近X的centroids集合Θ,结果是MOFcentroids在整个数据集上运行.将Θ′与X带入式(1)中计算出使其值最小的隶属度矩阵U,这可以看作以Θ′作为Fcentroids的初始ck(1≤k≤K),并执行一步确定X的隶属度矩阵U,通过U即可求出最终的聚类结果.实验中发现,通过采样方法获得的Θ′接近于在整个数据集上获得的Θ,当采样个数n′达到一定规模时不但没有降低算法的聚类性能,还能够有效提高其效率.需要注意的是部分属性中的部分属性值所占比例很少,本文中称其为稀有属性值,采样可能无法获得包含这些稀有属性值的样本,使得Θ′中不能够包含全体数据集所有的ω. 为了分析稀有属性值在聚类过程中的作用,对数据集Heart和Dermatology进行分析,用dj(k)表示第k个属性中的第j个属性值.Heart包含2个类并拥有303个样本和8个属性,其中第4个属性拥有3个属性值分别用d1(4),d2(4),d3(4)表示,其个数分别为151,4,148,显然其中的d2(4)为稀有属性值,采用Fcentriods运行后对各个类的置信度如表1所示.Dermatology包含6个类并拥有366个样本和33个属性,其中稀有属性值包括个数分别为4,6,4的d1(1),d4(23),d4(30)等,采用Fcentriods行后对各个类的置信度如表2所示.由表1和表2可见各稀有属性值的置信度在相应属性中均为最小,表明其对聚类的作用很小.另外,存在一些属性值的作用是完全可以忽略的,将其称为噪声属性值,如Dermatology的d2(6)只有1个,发现其置信度值非常小,在聚类前随机选取第6个属性的其他属性值将其替换. Table 1 The Confidence of Rare Attribute Value in Heart Table 2 The Confidence of Partial Rare Attribute Value in Dermatology (16) (17) 然后计算缺失属性值的置信度和新的置信度向量如式(18),且需对新向量归一化使元素的和为1. (18) 需要说明的是在本文实验中尚未遇到稀有属性值的置信度较大的情况,按照算法原理,通常稀有属性值的置信度相对较小,这里加以分析说明以更好地应对实际问题中可能遇到的特殊情况. 3.1 实验数据集 本文通过分类型人工数据生成器*http://www.datgen.com产生2个较高维的人工数据集500_50_3和1000_50_4,其中每个属性均具有4个属性值.选取UCI数据库的8个常用的真实数据集Soybean,Zoo,Promotor,Heart,Votes,Dermatology,DNA,Mushroom进行分析.其中,缺失属性值和噪声属性值随机选取相关属性的其他属性值替换,混合型的Heart只考虑其中的分类属性部分.各数据集的相关特性如表3所示: Table 3 The Feature of Experimental Datasets 3.2 聚类性能评估标准 聚类结果通过聚类准确度(accuracy,Acc)和调整的兰特指数(adjusted rand index,ARI)这2种指标进行评价.若用ai表示被正确分到第i个类中的目标数量,n表示所有目标的数量,则Acc的定义为 (19) ARI将类别看成是样本之间的一种关系,通过统计正确决策样本对数来评价聚类算法的性能.若ni表示类i中数据点的个数,nj表示簇j中数据点的个数,nij表示同时在类i和簇j中的数据点的个数,则ARI如式(20)所示,其取值最大为1,且越大的值表明聚类的结果越好. (20) 3.3 对比算法相关过程描述 本文算法与FKMd[2],NgFKMd[29],Fcentriods[3],GAFcentriods(genetic algorithm fuzzy centriods),NSGA-FMC[16]这5个算法的聚类性能进行对比分析.NgKMd是由Ng等人[4]对KMd的简单匹配方式进行改进的一种算法,由于本文均为模糊聚类算法,其模糊版本NgFKMd的相异性度量为 (21) 3.4 结果比较与分析 各算法通过MATLAB2010b编程运行,计算机的硬件配置为:Intel Core P7450,CPU主频为2.13 GHz,RAM为2 GB.对上述的5个算法以及本文算法MOFcentroids进行分析,求出聚类性能指标Acc和ARI.算法参数设置为:GAFcentriods与MOFcentriods的种群规模N=20,最大迭代数Tmax=40,此外T1=8,T2=10,而NSGA-FMC种群数取50,最大迭代数取50;所有GA型算法交叉概率均为Pc=0.8,变异概率Pmu=0.1.依据文献[2]中的建议,本文中FKMd及NgFKMd的模糊指数为m=1.1,其他算法的模糊指数一般均为m=1.2,某些明显具有更好效果的特殊取值在相关算法后标明.Fcentriods的最大迭代次数Maxgen=50,FKMd和NgFKMd的最大迭代次数Maxgen=100,且目标函数值不发生明显变化则停止,此外,式(15)中的β=0.1.数据集Soybean,Promotor,Zoo的规模较小,本文中均未执行采样操作;对其余7个数据集均执行采样操作,且采样规模均为n′=0.3n,以保证绝大部分属性的属性值都能被选取到,无法选取到的即为稀有属性值.各算法分别运行30次,记录并计算出Acc和ARI的均值及标准差如表4所示,其中对每个数据的最优指标值加粗,且有多个最优值时优先标明本文算法.为了更直观地比较各算法结果的统计分布情况,各算法对10种数据集ARI指标的箱线图如图1所示,并在图1中标明均值. Table 4 The Experimental Results of All Algorithms Continued (Table 4) Fig. 1 Boxplot of ARI values for different algorithms executed on the 10 datasets. 根据表4中的实验结果,首先比较Fcentriods与FKMd的各项指标值可以发现Fcentriods在聚类准确度与稳定性方面均具有较明显的优势,这也成为了本文算法能够获得比较满意结果的原因之一.由于Fcentriods对Soybean的聚类指标已达到最优无提升空间,对Votes和Mushroom的聚类指标也较高以致相关改进算法难以获得提升,这里可见本文算法对较小数据集和较大数据集均具有良好的聚类性能.对于数据集500_50_3,1000_50_4,Zoo,Promotor,Heart,Dermatology,DNA,本文算法相对于Fcentriods的Acc和ARI均具有比较明显的提升.其中可以发现尤其对2个人工数据集的提升效果非常明显,对于Acc分别提升了21.1%,26.2%;对于ARI分别提升了32.2%,20.47%.这是由于Fcentriods算法对这2个数据集的性能很不稳定,对于500_50_3能够获得Acc指标的最大值为0.70,最小值为0.34;对于1000_50_4能够获得Acc指标的最大值为0.86,最小值为0.26,因此其标准差较大分别为0.163和0.233.融入单目标和多目标进化算法之后均使其稳定性获得了较大的提升,有效改善了算法的聚类性能.而算法FKMd以及相应的2种改进算法对这2个人工数据集几乎是无效的,其原因值得进一步研究.在UCI的真实数据集中,3种FKMd型算法对数据DNA均可看作无效,且对Promotor仅获得很小的ARI值(对于NgFKMd和NSGA-FMC甚至为负数).Fcentriods算法对这2个数据集均具有一定的优势,不过其对DNA的Acc值虽然为0.501,高于FKMd的0.388,而ARI值仅为0.002,低于FKMd,这里表明采用多个指标的必要性,本文算法同时对这2个指标提升至0.528和0.116.进一步比较可见,NSGA-FMC的性能相对于FKMd有显著的提高,且相对于NgFKMd也有一定的提高.而本文算法对于各个数据集的Acc和ARI均高于NSGA-FMC,这也间接体现了Fcentriods相对于FKMd的优势.综合对比可见,除了少数情况外,本文算法的聚类指标值均为最大并已在表4中加粗标明,并且对多个数据集的标准差也很小,表明其具有较高的稳定性,因此可以判断出其具有最佳的聚类性能. 由图1可见,Fcentriods算法对2种人工数据集的上下限范围较大,与上文所提到的稳定性差相对应,并且其对数据集Soybean,Heart,Votes和Mushroom的上下限均相等,表现出非常高的稳定性.虽然本文算法对Heart和Mushroom的稳定性有较小的下降,但更高的上限值表明多目标聚类算法具有搜索到更精确解的能力.相对于Fcentriods而言,本文算法明显提高了对Zoo和Promotor的指标,而GAFcentriods对它们的聚类指标比Fcentriods更差,这里体现出将多目标引入到聚类过程中的优势.对于Dermatology和DNA,本文算法以及GAFcentriods的结果均获得了明显的改善.此外,值得注意的是图1中NSGA-FMC对Zoo的ARI均值与本文算法很接近,但是本文算法的Acc均值0.892明显高于NSGA-FMC的0.866,进一步表明了采用多个聚类评估指标的必要性. 由于算法Fcentriods对模糊指数m的选取比较敏感,这里分别取m为1.1,1.2,1.3,将Fcentriods和MOFcentriods对各数据集分别执行30次并求出Acc的均值及标准差记录至表5中.此外,由于2种算法对Votes的Acc值始终为0.881,对Soybean除Fcentroids在m=1.1时的Acc均值为0.979,其余均为1.000,表5中未给出相应的结果.由表5可见,Fcentriods受m值的影响很明显,尤其是对数据集Zoo,Promotor,Dermatology,取值不当会使算法性能很差,因此鲁棒性较差.本文通过先验的类标签信息可确定Fcentriods对于不同数据集的最佳m值,如表4中对Zoo的指标值是取m=1.1的结果,而现实的数据没有先验信息.本文算法在不同m值下均能够获得较高的Acc值,显示了较好的鲁棒性.因此,在Fcentriods中融入多目标进化算法能够有效解决对参数m敏感的问题,本文算法始终使用的是m=1.2. 此外,在MATLAB编程环境下,NgFKMd改进的相异性度量与Fcentriods基于置信度的相异性度量均需循环操作比较每一维而无法简化,NSGA-FMC中简单匹配相异性度量可通过MATLAB语句简化以提高效率,即只需执行一步计算数据向量与类中心向量不相等元素的长度作为相异性距离.因此,本文仅通过时间复杂度对各算法进行比较,用K表示类数,n表示样本个数(n′表示采样样本个数),D表示属性维数,s表示各算法的最大迭代数,N表示种群个数.由于各算法的时间计算主要依赖于每次迭代中类中心和划分矩阵的更新,FKMd更新类中心和划分矩阵的时间复杂度[2]分别为O(KnM)和O(knD),其中M为所有属性值个数总和,故其总体时间复杂度为O(Kn(D+M)s);Fcentriods更新模糊类中心和划分矩阵的时间复杂度[3]分别为O(KnD)和O(KTnD),其中T=max(nl),nl(1≤l≤D)为D维属性中各自包含的属性值的个数,故其总体时间复杂度为O(sKnD(T+1)).由于几种混合聚类算法的交叉算子均执行一步基算法,变异算子的计算可以忽略,故NSGA-FMC的总体时间复杂度为O(s(1+Pc)Kn(D+M)N);GAFcentriods和MOFcentriods在采样子集上的总体时间复杂度为O(s(1+Pc)Kn′D(T+1)N).本文算法的时间复杂度与类数、样本数及属性数均成线性关系,因此能够用于分析较大数据集.需要注意的是多数情况下无需达到最大迭代数即停止,如本文算法最少迭代10次左右便提前终止.Fcentriods和MOFcentriods对各数据集的平均运行时间的对比如表6所示: Table 5 The Acc of Fcentroids and MOFcentroids with Different Values of m Table 6 Average Runtime of Fcentroids and MOFcentroids 表6中,对数据集Soybean,Zoo,Promotor均未执行采样,其他7个数据集均给出执行采样和不执行采样的平均运行时间,并且在不同情况下提前终止时的迭代数不一致导致前者的运行时间并不一定是后者的0.3.在Fcentriods运行中其目标函数值只要相对于前一次迭代无明显变化即停止,而本文算法连续T1=8次迭代PF的最优值无明显变化才会停止.由表6可见,本文算法的运行时间均未达到Fcentriods的(1+Pc)N倍.当不执行采样操作时本文算法的运行时间相对较长,尤其对较大数据集DNA(维数也较高)和Mushroom的时间非常长,这也是现有的多目标聚类算法[14-16,25-27]均存在的问题.如在文献[16]中给出NSGA-FMC在未考虑任何时间效率方面的优化时对规模并不大的Soybean,Zoo,Votes的运行时间分别为76.56 s,220.69 s,191.52 s,而在文献[14]中给出对这3个数据集的运行时间甚至分别达到了120.49 s,530.47 s,780.28 s.本文通过采样以及提前终止准则能够较大程度地缩短时间,并且不会降低算法的聚类性能,硬件配置并不如文献[16],能够获得较满意的结果,MOFcent-riods较Fcentriods的最大倍数仅为对数据集Votes的8倍.此外,表6中均为执行提前终止准则的结果,为了分析其对算法运行效率的提升,图2给出了不执行提前终止准则(Termination1)和执行提前终止准则(Termination2)下的运行时间对比. Fig. 2 The average runtime of MOFcentroids for different algorithms with two kinds of terminations.图2 MOFcentroids对各数据集采用2种不同终止准则的平均运行时间 由图2可见,对于所有数据集,提前终止准则均有效地减少了运行时间,对于Promotor,1000_50_4,DNA,Mushroom这4个数据集而言,Termination 1比Termination 2的时间高了接近3倍,表明其迭代10多次即停止,若迭代40次则增加了大量不必要的计算开销,从而影响了算法的运行效率. 3.5 统计显著性分析 为了验证本文算法所获得的更佳聚类结果是统计显著的,本文采用t-test统计显著性测试进行分析,并在5%的显著性水平下计算出相应的p-value记录到表7中.这里对指标值Acc进行分析,比较本文算法与其他算法之间的p-values.首先,本文算法与其他算法之间的Acc不存在统计显著性差异作为零假设,那么备择假设即为在它们之间存在显著性差异.从表7可见,几乎所有的p-values均小于0.05,并且大部分情况下远小于该值,这表明零假设不成立,因此接受备择假设,即本文算法的Acc结果与其他算法间存在统计显著性差异而不是偶然发生的,类似的结果同样存在于ARI中.此外,对于GAFcentroids算法出现了比较多的统计不显著现象是符合规律的,因为对于这些不显著的数据集,其改进作用与本文算法比较相近,从表4和图1的结果可以看出两者的结果较接近,具有相似的统计分布.但是,GAFcentroids通过唯一的最优解确定聚类结果,而本文算法从非支配解集中确定聚类结果,因此其性能更可靠,从而对各数据集均能够获得较满意的聚类结果,体现出采用多目标优化的优势. Table 7 p-value Produced by t-test For Acc 本文将多目标优化理论引入到分类数据聚类算法Fcentriods中,提出一种新颖的多目标模糊中心点聚类算法MOFcentriods.通过与传统的单目标聚类算法以及目前最新的多目标聚类算法NSGA-FMC的实验对比,表明本文算法在聚类准确性与稳定性方面具有较高的优势,且其鲁棒性也较高.与此同时,针对多目标聚类算法通常时间较长的问题,本文采用一种基于采样的方法,在能够代表数据点统计分布的样本子集上获得逼近整体数据集的聚类表达,有效提高了算法的效率.不过,由于多目标聚类算法在时间方面高于传统的聚类算法,不适用于处理规模很大的数据集.并且,由于分类数据中属性为离散型,若在聚类迭代过程中执行采样将使算法无法顺利执行,而对于属性为连续型的数值数据则不会产生相应的问题,接下来可结合聚类过程中的采样以进一步研究能够有效面向较大规模数值数据的多目标聚类算法. [1]Huang Z. Extensions to thek-means algorithm for clustering large data sets with categorical values[J]. Data Mining and Knowledge Discovery, 1998, 2(3): 283-304 [2]Huang Z, Ng M K. A fuzzyk-modes algorithm for clustering categorical data[J]. IEEE Trans on Fuzzy Systems, 1999, 7(4): 446-452 [3]Kim D W, Lee K H, Lee D. Fuzzy clustering of categorical data using fuzzy centroids[J]. Pattern Recognition Letters, 2004, 25(11): 1263-1271 [4]Ng M K, Li M J, Huang J Z, et al. On the impact of dissimilarity measure ink-modes clustering algorithm[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2007, 29(3): 503-507 [5]Liang Jiye, Bai Liang, Cao Fuyuan.K-modes clustering algorithm based on a new distance measure[J]. Journal of Computer Research and Development, 2010, 47(10): 1749-1755 (in Chinese) (梁吉业, 白亮, 曹付元. 基于新的距离度量的K-Modes聚类算法[J]. 计算机研究与发展, 2010, 47(10): 1749-1755) [6]He Zengyou, Xu Xiaofei, Deng Shengchun. Attribute value weighting ink-modes clustering[J]. Expert Systems with Applications, 2011, 38(12): 15365-15369 [7]Cao Fuyuan, Liang Jiye, Li Deyu, et al. A dissimilarity measure for thek-modes clustering algorithm[J]. Knowledge-Based Systems, 2012, 26: 120-127 [8]Gan G, Wu J, Yang Z. A genetic fuzzyk-modes algorithm for clustering categorical data[J]. Expert Systems with Applications, 2009, 36(2): 1615-1620 [9]Maulik U, Bandyopadhyay S, Saha I. Integrating clustering and supervised learning for categorical data analysis[J]. IEEE Trans on Systems, Man and Cybernetics, Part A: Systems and Humans, 2010, 40(4): 664-675 [10]Chan E Y, Ching W K, Ng M K, et al. An optimization algorithm for clustering using weighted dissimilarity measures[J]. Pattern Recognition, 2004, 37(5): 943-952 [11]Bai Liang, Liang Jiye, Dang Chuangyin, et al. A novel attribute weighting algorithm for clustering high-dimensional categorical data[J]. Pattern Recognition, 2011, 44(12): 2843-2861 [12]Bai Liang, Liang Jiye, Dang Chuangyin, et al. A novel fuzzy clustering algorithm with between-cluster information for categorical data[J]. Fuzzy Sets and Systems, 2013, 215: 55-73 [13]Bai Liang, Liang Jiye. Thek-modes type clustering plus between-cluster information for categorical data[J]. Neurocomputing, 2014, 133: 111-121 [14]Mukhopadhyay A, Maulik U, Bandyopadhyay S. Multiobjective genetic algorithm-based fuzzy clustering of categorical attributes[J]. IEEE Trans on Evolutionary Computation, 2009, 13(5): 991-1005 [15]Saha I, Maulik U. Incremental learning based multiobjective fuzzy clustering for categorical data[J]. Information Sciences, 2014, 267: 35-57 [16]Yang C L, Kuo R, Chien C H, et al. Non-dominated sorting genetic algorithm using fuzzy membership chromosome for categorical data clustering[J]. Applied Soft Computing, 2015, 30: 113-122 [17]Iam-On N, Boongeon T, Garrett S, et al. A link-based cluster ensemble approach for categorical data clustering[J]. IEEE Trans on Knowledge and Data Engineering, 2012, 24(3): 413-425 [18]Can Gao, Pedrycz W, Miao Duoqian. Rough subspace-based clustering ensemble for categorical data[J]. Soft Computing, 2013, 17(9): 1643-1658 [19]Saha I, Sarkar J P, Maulik U. Ensemble based rough fuzzy clustering for categorical data[J]. Knowledge-Based Systems, 2015, 77: 114-127 [20]Cao Fuyuan, Liang Jiye, Bai Liang. A new initialization method for categorical data clustering[J]. Expert Systems with Applications, 2009, 36(7): 10223-10228 [21]Bai Liang, Liang Jiye, Dang Chuangyin, et al. A cluster centers initialization method for clustering categorical data[J]. Expert Systems with Applications, 2012, 39(9): 8022-8029 [22]Khan S S, Ahmad A. Cluster center initialization algorithm fork-modes clustering[J]. Expert Systems with Applications, 2013, 40(18): 7444-7456 [23]Ji Jinchao, Pang Wei, Zhou Chunguang, et al. A fuzzyk-prototype clustering algorithm for mixed numeric and categorical data[J]. Knowledge-Based Systems, 2012, 30: 129-135 [24]Ji Jinchao, Bai Tian, Zhou Chunguang, et al. An improvedk-prototypes clustering algorithm for mixed numeric and categorical data[J]. Neurocomputing, 2013, 120: 590-596 [25]Bandyopadhyay S, Maulik U, Mukhopadhyay A. Multiobjective genetic clustering for pixel classification in remote sensing imagery[J]. IEEE Trans on Geoscience and Remote Sensing, 2007, 45(5): 1506-1511 [26]Saha I, Maulik U, Plewczynski D. A new multi-objective technique for differential fuzzy clustering[J]. Applied Soft Computing, 2011, 11(2): 2765-2776 [27]Ma Ailong, Zhong Yanfei, Zhang Liangpei. Adaptive multiobjective memetic fuzzy clustering algorithm for remote sensing imagery[J]. IEEE Trans on Geoscience and Remote Sensing, 2015, 53(8): 4202-4217 [28]Ng R T, Han Jiawei. Clarans: A method for clustering objects for spatial data mining[J]. IEEE Trans on Knowledge and Data Engineering, 2002, 14(5): 1003-1016 [29]Ng M K, Jing Liping. A new fuzzyk-modes clustering algorithm for categorical data[J]. International Journal of Granular Computing, Rough Sets and Intelligent Systems, 2009, 1(1): 105-119 Zhou Zhiping, born in 1962. PhD, professor in the School of Internet of Things Engineering, Jiangnan University. His main research interests include intelligent detection, information safety, image processing. Zhu Shuwei, born in 1990. Master from Jiangnan University. Student member of China Computer Federation. His main research interests include pattern recognition and data mining (zswjiang@163.com). Zhang Daowen, born in 1989. Master candidate in Jiangnan University. Student member of China Computer Federation. His main research interests include data mining (zdwjndx@gmail.com). Multiobjective Clustering Algorithm with Fuzzy Centroids for Categorical Data Zhou Zhiping, Zhu Shuwei, and Zhang Daowen (SchoolofInternetofThingsEngineering,JiangnanUniversity,Wuxi,Jiangsu214122) It has been shown that most traditional clustering algorithms for categorical data that only optimize a single criteria suffer from some limitations, thus a novel multiobjective fuzzy clustering is proposed, which simultaneously considers within-cluster and between-cluster information. The lately reported algorithms are all based onK-modes, and the more accurate algorithm fuzzy centroids is utilized as the base algorithm to design the proposed method. Fuzzy membership is used as chromosome that is different from traditional genetic based hybrid algorithms, and a set of optimal clustering solutions can be produced by optimizing two conflicting objectives simultaneously. Meanwhile, a termination criterion in advance which can reduce unnecessary computing cost is used to judge whether the algorithm is steady or not. To further improve the efficiency of the proposed method, fuzzy centroids can be calculated using a subset of the dataset, and then the membership matrix can be calculated by these centroids to obtain the final clustering result. The experimental results of 10 datasets show that the clustering accuracy and stability of the proposed algorithm is better than the state of art multiobjective algorithm, and also the computing efficiency is improved to a large extern. categorical data; clustering; multiobjective optimization; fuzzy centroids; Pareto-optimal solutions 2015-06-10; 2015-12-22 国家自然科学基金项目(61373126);江苏省自然科学基金项目(BK20131107);江苏省产学研联合创新资金-前瞻性联合研究基金项目(BY2013015-33) TP181 This work was supported by the National Natural Science Foundation of China (61373126), the Natural Science Foundation of Jiangsu Province of China (BK20131107), and the Cooperative Industry-Academy-Research Innovation Foundation of Jiangsu Province of China (BY2013015-33).




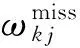


3 实验结果与分析












4 结束语




