基于多维分形理论的地质灾害地球物理调查

王 萌，王珺璐，沈效群，冯 兵，周锡华

(1.中国国土资源航空物探遥感中心，北京 100083;2.中国地质科学院 地球物理地球化学勘查研究所，河北 廊坊 065000;3.长安大学 地质工程与测绘学院，陕西 西安 710054)



基于多维分形理论的地质灾害地球物理调查

王 萌1，王珺璐2，沈效群1，冯 兵3，周锡华1

(1.中国国土资源航空物探遥感中心，北京 100083;2.中国地质科学院 地球物理地球化学勘查研究所，河北 廊坊 065000;3.长安大学 地质工程与测绘学院，陕西 西安 710054)

近地表地质灾害具有多期次和空间相关性等特点，它们所产生的地球物理场会呈现空间自相似性，满足多重分形理论，可以利用分形、分维理论进行地球物理数据分析。将C-A多重分形模型应用于放射性地裂缝勘探的数据处理，将分维方法应用于TEM煤田采空区勘探的数据处理，效果明显。分形与分维理论考虑了异常的空间形态和变化性以及地球物理场的各向异性和广义自相似性，可以分析地球物理场的空间分布，通过压制背景干扰来突出局部异常；可以借助分维数，表征空间不规则形体的复杂程度，揭示局部随机性和整体确定性特征。分形与分维理论为近地表地质灾害地球物理数据提供了十分有效的分析处理技术。

分形；分维；近地表地质灾害；放射性能谱；TEM

1 引 言

随着我国工业化、城镇化步伐的加快，能源矿产等资源的不断开采，生态环境及近地表地质条件逐渐恶化，地质灾害问题变得尤为突出。据2014年全国地质灾害通报显示，全国全年共发生地质灾害10 907起，共造成400人死亡或失踪，直接经济损失54.1亿元。地质灾害类型主要包括滑坡、崩塌、泥石流、地面塌陷、地裂缝和地面沉降等，其诱发因素既有自然因素，也有人为因素。自然因素主要是降水，人为因素主要是采矿及切坡。例如降水诱发非稳定地质体出现滑坡、裂缝；煤田采空诱发塌陷、突水等。

近几十年来，许多学者采用地球物理方法对地质灾害探测进行了研究。许德树等[1]、邓居智等[2]、郭秀军等[3]分别采用高精度重力、放射性能谱、高密度电法等方法开展滑坡监测工作。王国群等[4]、李忠生[5]、韩许恒等[6]分别采用探地雷达、地震勘探、氡射气测量等方法开展地裂缝探测工作。冯兵等[7]、程建远等[8]、余传涛等[9]、王宾等[10]、夏中广等[11]分别采用瞬变电磁法、地震勘探、双频激电等方法进行矿产采空区探测。薛国强等[12]、钟世航[13]、孙怀凤等[14]分别研究了采用瞬变电磁法、陆地声呐法、核磁共振法进行隧道超前探测。虽然地球物理及相关技术在近地表地质灾害勘查及治理中成果显著，但是如何更加有效地利用地球物理数据研究近地表地质灾害，已成为人们关注的重要问题。

多重分形分析方法是一种用于研究具有自相似性分布规律的有效方法，在分析复杂的非线性系统方面取得了良好的效果。成秋明、李庆谋等学者先后提出了采用C-A、S-A、MSVD、W-A等方法进行地球物理地球化学场的分析、分离与重建[15-20]；石雨田等人采用分维定量描述裂缝发育程度[21]；李学民等人采用分维方法尝试提取大地电磁中的构造信息[22]；曹茂森等人提出了小波与分形优势结合的地震异常检测方法[23]；梁齐端等人分析了自然伽马测井资料，认为自然伽马曲线的分形特征与地层中放射性富集程度有关[24]；王倩等人基于分形理论中的求和法对遥感蚀变异常进行了提取和分级[25]；桂蕾等人采用广义关联维的方法对滑坡地表监测位移进行了分析[26]。笔者将C-A多重分形模型应用到地裂缝放射性能谱勘探的数据处理中，确定了异常限，对测区进行了危险性评价；采用分维的思路求取瞬变电磁感应电动势的关联维，确定了煤田采空区位置。该研究为近地表地质灾害地球物理数据处理提供了有效的分析处理技术。

2 原理与算法

在地学领域中，通常采用统计学方法确定地球物理信号的异常。例如，在地球化学异常评价及部分地球物理场的问题中，常以均值、标准差等指标划分异常下限。这种计算方法是以样品呈统计学规律为前提的，实际应用中受限于场的特殊性及其他因素的干扰。虽然近地表地质灾害的发生具有突发性，但其实质上是不同期次、不同地质作用相互叠加并瞬时爆发的结果，具有明显的多期次性。另外，地质灾害的形成及演化受地质环境、水文环境、外部诱发因素等多重因素的影响[15]，这些因素共同作用导致岩石的电阻率及各种物理性质的分布表现出很强的非匀质性。在一定的范围内，地下介质的物性在不同尺度上存在着空间相关性。由于这类地质过程往往具有多期次和空间相关性等特点，它们所产生的地球物理场会呈现空间自相似性，满足多重分形理论[17]。因此，可以利用分形、分维理论进行地球物理数据分析处理。

2.1 C-A分形模型与算法

成秋明基于岩石地球化学的研究，提出采用“密度-面积”(C-A)分形模型度量密度与面积的各向异性自相似性[15,28]：

N(r)=Cr±D

(1)

其中：r表示某一特征尺度的阈值；N(r)表示特征尺度大于或小于某一阀值r的样本个数或区域面积；随着阈值r的升高，N(r)逐渐减小。分维数D与比例常数C刻画了“密度-面积”变化的复杂程度。为提取分维数D，将式(1)两边取对数有：

LnN(r)=Ln(C)±DLn(r)

(2)

当具有严格的自相似性时，在双对数坐标系上r-N显示为一条直线。对于具有客观统计自相似性的数据，在一定的尺度范围内可以近似为直线。异常与背景具有不同的斜率，对表现为不同斜率的点进行最小二乘线性拟合，不同线段所对应的分界值可以作为区分背景场和异常场的异常限。地球物理中的位场等也具有自相似性或统计自相似性，满足分形或多重分形分布，可以用“密度-面积”分形模型进行背景场与异常场的分离。

2.2 关联维D2的计算方法

分维的定义有很多种，采用较广泛的是联维数D2，其数学计算方法简单有效。采用嵌入空间法计算联维数D2[21,22,29]。

对于一个原始的时间序列信号x1,x2,x3…,xN，首先要建立相空间。假设相空间的分维数为m，以前m个时间序列点组成相空间的第1个点Y1(x1,x2,x3…,xm)；延迟τ个点后截取m个时间序列点组成相空间的第2个点Y2(x1+τ,x2+τ,x3+τ…,xm+τ)；依次类推扩展得到m维相空间：

(3)

式中，τ为延迟点数，i=1,2,…,n,n≤(N-m)/τ+1，当τ=1时n=N-m+1。

计算相空间内任意一对相点Yi与Yj之间的距离：

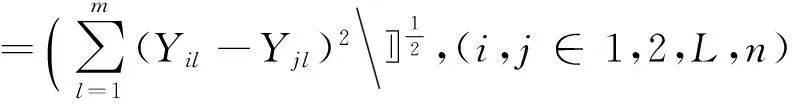
(4)

统计任意一对相点距离小于标度r的点对数目在所有点对中所占的比例C(r)：

(5)

式中，H(x)为Heavside函数。随着标度r的升高，比例C(r)逐渐减小。当所计算的时间序列有严格的自相似性时，在双对数坐标系下，lgr与lgC(r)为一条直线，其斜率即D2。对于统计自相似性，可选取线性度较好的一段进行最小二乘拟合，计算拟合直线的斜率，即可得到关联维数D2。

由嵌入空间法方法计算得到的关联维数D2，表示统计意义下的自相似性参数，计算结果与参数选取有关。因此，要选定合适的参数进行计算。延迟点数可以采用自相关方法进行计算，一般延迟点数τ=1；嵌入维数可以由小到大进行试算，选择曲线拟合较好的，一般嵌入维数m>8;r取值应限定在重构空间中各点距离的最大值与最小值之间，可以按等间距、等比例、等指数比例方式取值，一般r的个数大于20。

3 应用研究实例

3.1 地裂缝勘探中放射性能谱C-A分形特征

地下的放射性元素在衰变过程中产生的新子体具有很强的渗透性，构造运动和地下水的不断循环均为放射性物质的迁移和积聚提供了有利条件。在同一地区的地层中，构造断裂及非构造裂隙区域的放射性浓度偏高，形成“双峰形”高值异常特征。因此，可以利用放射性异常的空间分布规律研究地裂缝的平面位置等信息。

陕西省韩城市龙亭镇长期受到地裂缝地质灾害的威胁，该区东面濒临黄河谷地，区内地裂缝可能与黄土湿陷、边坡失稳有关。另外，区内可能存在北东向隐伏的华县—朝邑—禹门口大型正断层，是地裂缝多发的构造因素。在该区开展放射性能谱测量工作，探测该区的地裂缝分布范围，研究地裂缝的成因。野外工作采用ARD型便携式多道伽玛能谱仪，测量得到相应点位的U、T、K及TC含量。每个测点测量2次，每次测量1分钟。区内共布设14条放射性能谱剖面，控制总长度5 115 m。

将测量得到的数据进行网格化后，采用C-A分形法确定其异常下限。在TC的C-A双对数坐标散点图上(图1)，其“密度-面积”关系可用四条直线段拟合，说明TC密度在空间分布上存在多个无标度区。

采用最小二乘法计算得到的方程为：

N(r)=12.938r-0.25311.102≤r<14.939 N(r)=15.833r-1.32414.939≤r<17.021 N(r)=21.292r-3.25017.021≤r<20.459 N(r)=12.424r-0.31220.459≤r<23.623 采用C-A分形模型得到的分界点为14.939、17.021、20.459。对TC含量等值线图进行分级显示(图2)，结合已知的地裂缝点位及地质构造环境进行分析，可以看出：从低值区拟合的直线即图2中蓝色区域，该区为TC的背景区，地裂缝发育不明显，危险性较低；第二段直线与第三段直线即图2中绿色区域和黄色区域，这两个区域为区域TC异常区，可能主要与NE向隐伏断裂有关，黄色区内地裂缝也相对发达，危险性相对较高；第四段即图2中的红色区域，该区为局部TC异常区，可能受到了NE向与河岸边坡滑塌的多重影响，区内地裂缝最发达，危险性最高；并且图中部分红色点状异常区与调查已知的地裂缝位置吻合。

因此，利用C-A方法确定放射性能谱数据的异常限，可以对放射性异常进行分区，分析地裂缝类型与生成原因，进而进行危险性分区，为搬迁工作提供依据。

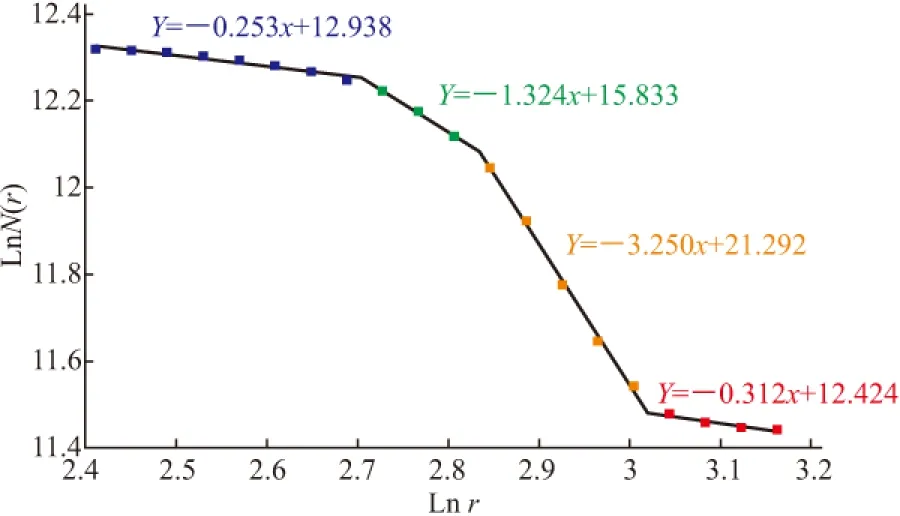
图1 放射性能谱TC数据的Lnr-LnN(r)拟合图Fig.1 Fitting map of radioactive energy spectrum Lnr-LnN(r) TC data

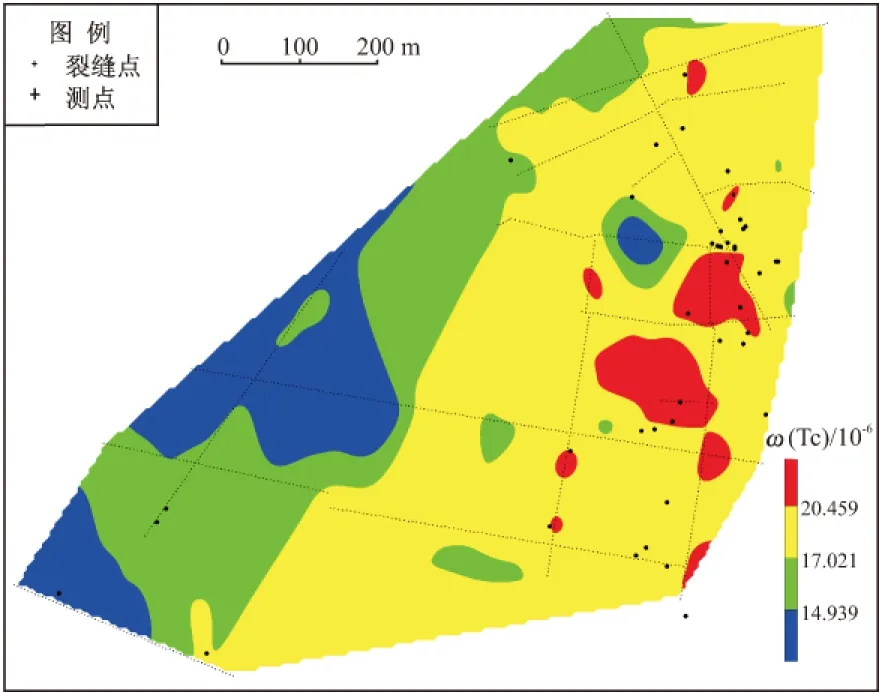
图2 放射性能谱TC含量(单位：×10-6)分级显示Fig.2 TC the anomaly distribution map of radioactive energy spectrum data

3.2 煤田采空区勘探中瞬变电磁分维特征

地下的煤层被采出后，在岩层内会形成一个形态复杂，有一定规模的空间。随着时间的推移，上覆岩层就会在地球重力的作用下逐渐断裂、塌陷，地下水就会侵入，采空区的电阻率发生变化，会出现相对高阻或低阻异常区。关联维数能反应地下介质的复杂程度，因此可以间接反应采空区信息。

在山西省某煤矿区开展了瞬变电磁探测工作，确定该区的煤层采空区分布范围，并分析其富水性。勘探区位于太行山脉南段西侧，沁水盆地南缘，为低山丘陵地带；井田内多为黄土覆盖，基岩零星出露，地形相对高差较小；3、9、15号煤层为可采煤层，其中3号煤层为主要可采煤层，煤层厚4.80～8.35 m，结构简单，顶板为砂岩、砂质泥岩，底板为砂质泥岩或砂岩。野外TEM测量中采用大定源回线装置，发射线框120 m×200 m，发射频率25 Hz，供电电流8 A，叠加次数200次，观测磁场垂直分量。

选取其中一条测线，进行瞬变电磁信号的分维特征研究。计算每一个测点的关联维数D2，计算时嵌入维数m=15，延迟点数τ=1,r分段数为30。选择采空区正上方1 690点与正常地层位置1 560点为例，Lnr-LnC(r)数据拟合得到的曲线(图3)出现不同的斜率，1 560点关联维数D2=2.037，1 690点关联维数D2=2.545。采空区上方的分维数大于正常地层。

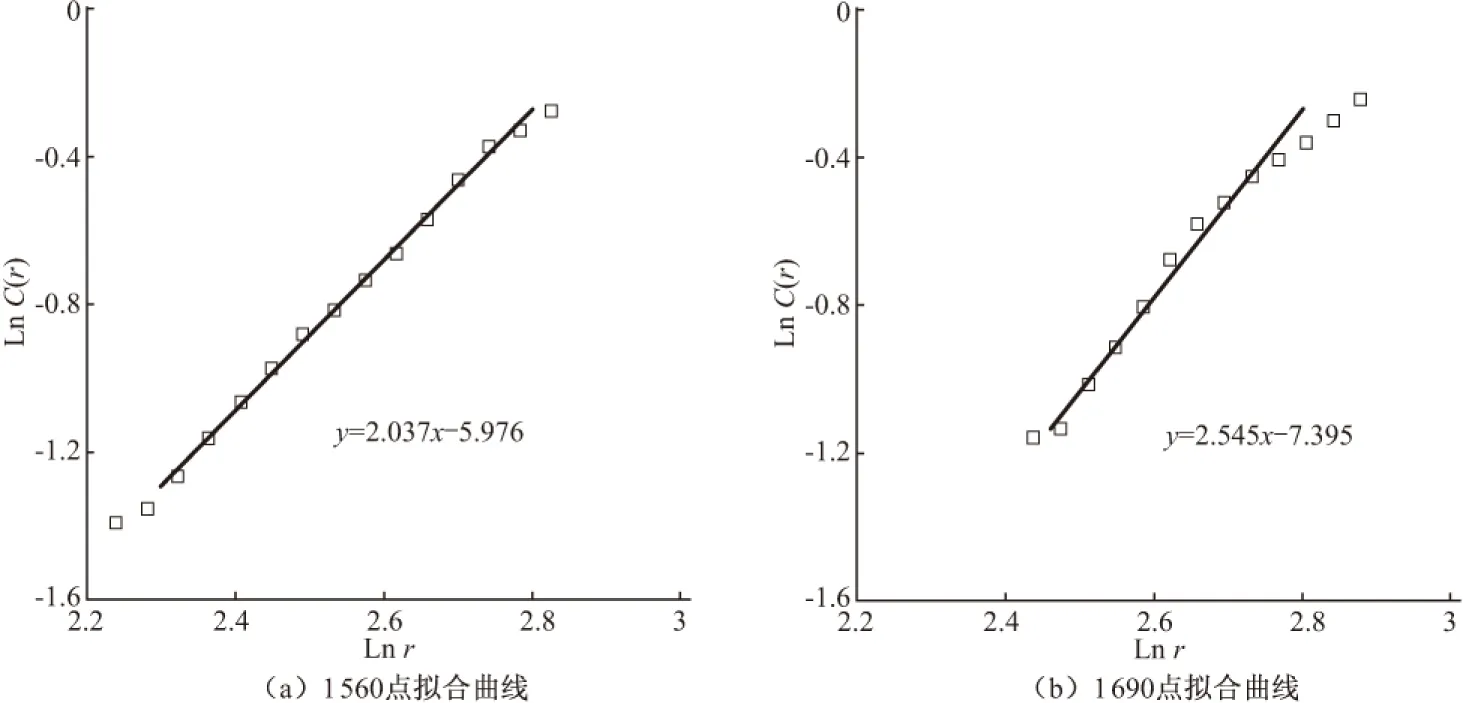
图3 Lnr-LnC(r)拟合曲线Fig.3 Lnr-LnC(r) fitting curve(a)1 560 fitting curve; (b)1 690 fitting curve

图4(b)是该测线根据测得的感应电动势计算得到的晚期视电阻率断面图(单位：Ω·m)，图中的1 590～1 830点之间为调查已知的采空区，晚期视电阻率等值线出现向下凹陷的现象；在1 460点附近存在高压线干扰，晚期视电阻率等值线较凌乱。图4(a)是根据测量得到的随时间变化的感应电动势求得的关联维数D2曲线。从图中可以看出，1 590～1 830点之间出现双峰型的高值异常区，与已知煤田采空区对应良好；1 460点附近出现突兀的单峰型异常，与高压线位置吻合。因此，根据野外获得的TEM信号可以快速计算关联维数D2，在一定程度上可以区分干扰，推断采空区分布范围。

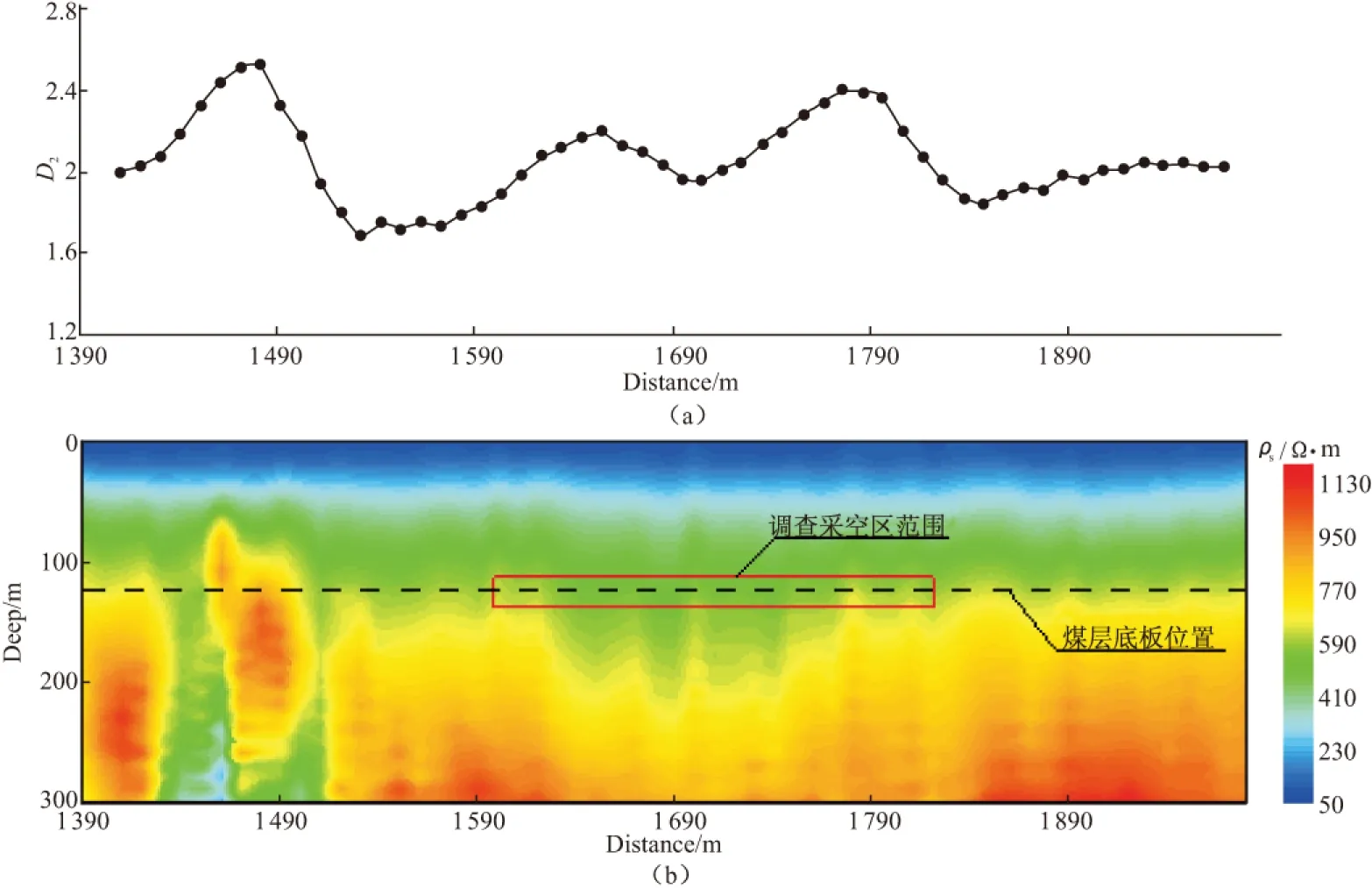
图4 关联维数D2曲线(a)和TEM晚期视电阻率断面(b)Fig.4 Correlation dimension of D2 curve (a) and the late apparent resistivity section diagram of TEM (b)

4 结 论

1)近地表地质灾害具有多期次和空间相关性等特点，它们所产生的地球物理场会呈现空间自相似性，满足多重分形理论，可以利用分形、分维方法进行地球物理数据处理分析。

2)对分形与分维方法在近地表地质灾害地球物理数据处理中的应用进行了分析，效果明显。将C-A多重分形模型应用到地裂缝放射性能谱勘探的数据处理中，确定了异常限，对测区进行了危险性评价；采用分维方法求取瞬变电磁信号的关联维，确定了煤田采空区位置。

3)分形与分维理论考虑了异常的空间形态和变化性以及地球物理场的各向异性和广义自相似性，可以分析地球物理场的空间分布，通过压制背景干扰来突出局部异常；可以借助分维数，表征空间不规则形体的复杂程度，揭示局部随机性和整体确定性特征。分形与分维理论为近地表地质灾害地球物理数据处理提供了十分有效的分析处理技术。

[1]许德树,卢景奇,李元厚,等.高精度重力测量在香港石硖尾滑坡治理区的应用[J].物探与化探,2004,28(4):345-348.

[2]邓居智,叶树林,刘庆成.氡及其子体测量方法在滑坡勘查中的应用研究[J].地质与勘探,2008,44(1):113-116.

[3]Guo Xiujun, Huang Xiaoyu, Jia Yinggang. Forward modeling of different types of landslides with mult-electrode electric method (English)[J]. Journal of Chinese Geophysical Society Applied Geophysics, 2005, 2(1):14-20+70.

[4]王国群.不同成因地裂缝探地雷达图像特征[J].物探与化探,2009,33(3):345-349.

[5]李忠生.构造地裂缝的成因与地震勘探[J].煤田地质与勘探,2004,32(4):54-56.

[6]韩许恒,郁春霞.氡射气测量在西安地裂缝勘察中的应用研究[J].工程地质学报,1997,5(1):66-72.

[7]冯兵,孟小红,张斌.TEM框内回线装置发射框边界影响及消除方法[J].煤田地质与勘探,2010,38(5):61-66.

[8]程建远,孙洪星,赵庆彪,等.老窑采空区的探测技术与实例研究[J].煤炭学报,2008,33(3):251-255.

[9]余传涛,刘鸿福,高建平.双频激电法在探测煤矿采空区的尝试[J].地球物理学进展,2008,23(5):1 603-1 609.

[10]王宾,韩晓南,王康东.综合物探方法在采空塌陷区地质灾害勘查中的应用[J].工程地球物理学报,2013,10(5):725-729.

[11]夏中广,郭莹.电法勘探在某辉锑矿采空区探测中的应用[J].工程地球物理学报,2013,10(5):676-682.

[12]薛国强,李貅.瞬变电磁隧道超前预报成像技术[J].地球物理学报,2008,51(3):894-900.

[13]钟世航.陆地声纳法的原理及其在铁路地质勘测和隧道施工中的应用[J].中国铁道科学,1995,16(4):48-55.

[14]孙怀凤,李术才,李貅,等.核磁共振测深进行隧道超前地质预报的可行性[J].山东大学学报(工学版),2013,43(1):92-97+103.

[15]Cheng Q, Agterberg F P, Ballantyne S B. The separation of geochemical anomalies from background by fractal methods[J]. Journal of Exploration,1994,51(2):109-130.

[16]成秋明.非线性成矿预测理论:多重分形奇异性-广义自相似性-分形谱系模型与方法[J].地球科学-中国地质大学学报,2006,31(3):337-348.

[17]成秋明,张生元,左仁广,等.多重分形滤波方法和地球化学信息提取技术研究与进展[J].地学前缘,2009,16(2):185-198.

[18]Lovejo y S, Schertzer D. Scaling and multifractal fields in the solid earth and topography. Nonlinear Processes of Geophysics，2007，14(4)：465-502.

[19]李庆谋,刘少华.地球物理信号能量(密度)多维分形及应用[J].地球物理学进展,2001,16(1):24-30.

[20]李庆谋,刘少华.分形噪声、(多维)分形滤波及地球物理测井曲线处理应用[J].物探化探计算技术,2001,23(1):37-42.

[21]石雨田,潘保芝.分维的应用——定量描述裂缝发育程度[J].物探与化探,2000,24(6):426-430+437.

[22]李学民,曹俊兴,刘柏红.分形理论在提取大地电磁资料构造信息中的应用[J].石油物探,2004,43(3):245-247.

[23]曹茂森,任青文,王怀洪.基于小波与分形理论的地震异常检测[J].地球物理学报,2005,48(3):672-679.

[24]梁齐端,赵世龙,丁忙生.自然伽马测井曲线的分形特征分析[J].物探与化探,2006,30(3):240-243.

[25]桂蕾,殷坤龙.基于多重分形理论的滑坡地表监测位移分析[J].中南大学学报(自然科学版),2014,45(11):3 908-3 914.

[26]王倩,陈建平.基于分形理论的遥感蚀变异常提取和分级[J].地质通报,2009,28(2/3):285-288.

[27]成秋明.空间自相似性与地球物理和地球化学场的分解方法[J].地球物理学进展,2001,16(2):8-17.

[28]张焱,周永章.多重地球化学背景下地球化学弱异常增强识别与信息提取[J].地球化学,2012,41(3):278-291.

[29]于青.关联维数计算的分析研究[J].天津理工学院学报,2004,20(4):60-62.

Geophysical Exploration of Geological Hazards Based on Multi-fractal Theory

Wang Meng1,Wang Junlu2，Shen Xiaoqun1,Feng Bing3，Zhou Xihua1

(1.ChinaAeroGeophysicsSurvey&RemoteSensingCenterforLandandResources,Beijing100083,China；2.InstituteofGeophysicalandGeochemicalExploration,CAGS,LangfangHebei065000,China；3.CollegeofGeologyEngineeringandGeomatics,Chang’anUniversity,Xi’anShanxi710054,China)

The near surface geological disasters have several stages and spatial correlation characteristics, and its geophysical field which shows the spatial self similarity to meet the multi-fractal theory. The multi-fractal theory and multi-dimension theory can be used in the geophysical data processing. C-A multi-fractal model can be applied to the data process from radioactive ground fissures exploration, and fractal dimension method can be applied to the data process from TEM coalfield goaf exploration. The effect is obvious. The theory of fractals and fractal dimension considered abnormal spatial form, spatial variability, anisotropic geophysical fields and generalized self-similarity. Using the multi-fractal method, the spatial distribution of geophysical fields can be analyzed, and the background signal suppressing can highlight the local anomalies. Using the fractal dimension, the complexity of the space of irregular form can be characterized, and the local randomness and the overall deterministic characteristics can be revealed. The theory of fractals and fractal dimension provides the very effective analytical processing technology for geophysical data processing about near-surface geological disasters.

fractal; fractal dimension; near-surface geological disasters; radioactive energy spectrum; TEM

1672—7940(2016)02—0202—06

10.3969/j.issn.1672-7940.2016.02.012

国家灾害地质调查项目(编号：1212010914013 )；国家高技术研究发展计划(编号：2013AA063902)

王 萌(1987-)，女，硕士，主要从事重磁数据处理与反演方面的研究。E-mail：mengmengcello@sina.com

P631

A

2015-07-10