几种典型内部排序算法性能分析
陶圣哲
摘要:目前排序算法的应用越来越广泛,其目的是方便记录的查找、插入及删除。本文从算法时间复杂度、空间复杂度及稳定性方面对冒泡排序、选择排序、插入排序以及归并排序进行了分析,并通过对比实验,对比了四种算法在不同数据规模时的对比次数、移动次数、交换次数以及时间,通过分析得出在数据量较大时选择归并排序,数据量较小时可以选择选择排序,数据大部分有序时可以选择插入排序的结论。
关键词:排序算法;性能;复杂度
中图分类号:TP311 文献标识码:A 文章编号:1009-3044(2016)26-0026-04
1绪论
近几年互联网的发展速度越来越快,涉及的领域越来越广,同时对计算机的性能要求也越来越高,基于目前硬件存储性能的限制,科研人员一直致力于计算机性能的优化,在目前的众多方法中,排序算法的优化及选择是研究的重点,排序算法的性能优劣直接影响到程序执行的性能。排序算法目前广泛应用于各个行业领域,例如网站搜索的排序,推荐的先后等等,重要性不言而喻。排序算法是依照一种规则对数据位置进行确定的算法,正是由于排序算法的重要性,人们对排序算法的研究从未停止,先后发明了适合于各种情况的排序算法。本文主要通过对几种典型的排序算法进行算法性能分析,通过算法执行的时间效率、空间效率以及算法稳定性对几种算法进行比较[1]。
2排序算法
排序算法数据处理规模的不同导致算法使用处理器的不同,一般将排序算法分为内部排序和外部排序。内部排序是指算法的整个处理过程完全在计算机内存中进行的排序算法,这是基于算法的数据估摸相对比较小,计算机内存能够满足计算机读取存储的需求,本文重点讨论的是内部排序中的冒泡排序、选择排序、插入排序、归并排序四种排序算法。外部排序一般需要处理的数据比较大,计算机内存无法满足待排序对象的一次存储,待排序记录需要在计算机内部存储器以及外部存储器之间进行切换来满足数据量的要求,进而实现对整个文件的排序[2]。
2.1冒泡排序
冒泡排序的基本思想是:通过不断比较相邻两个数的大小,并进行相应的调整使得最后所有数据达到有序,之所以称为冒泡排序是由于每一趟排序只比较出一个最大或最小的数出来,类似于冒泡。
具体排序过程如下:
1)在进行首次排序过程时将第一个数与第二个数比较,小数在前大数在后,之后是第二个数据和第三个数据按照相同的方式进行比较,同时按照小数在前大数在后的规则进行调整次序,不断进行比较交换调整直至最后两个数比较完毕最大的数据在最后一个,此时第一趟比较结束。
2)之后进行第二次排序,从第一个数据按照第一趟排序的规则依次比较排序直至倒数第二个数比较完毕,此时第二大的数据在倒数第二的位置。
3)之后按照相同的规则进行比较直到最后只剩下一个数据,此时排序完成。
冒泡排序算法的程序如下所示:
void paixu::bubblesort(int r[],long m,long n)
{for(i=m;i<=n-1;i++)
{for(j=n;j>=i+1;j--)
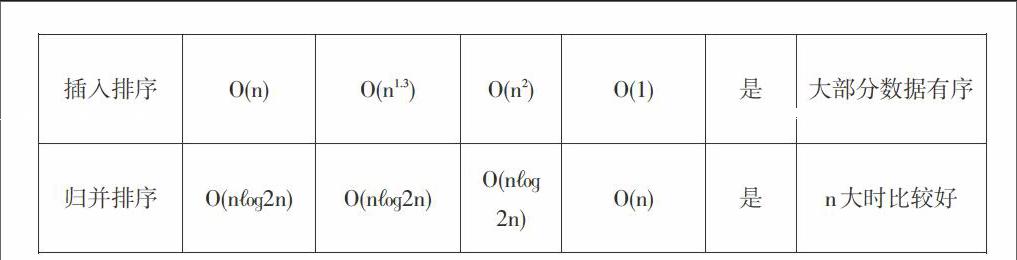
{if(r[j] {temp=r[j]; r[j]=r[j-1]; //交换 r[j-1]=temp; exchanges=1; exchange++;}} if(exchanges==0) //本趟无交换发生,则结束 return;}} 如果冒泡排序初始的数据所有的记录按照关键字有序的序列的话此时是最好的情况,只需进行一次冒泡,进行n-1次比较便可完成排序,由于所有记录均是关键字有序所以不需要进行移动,时间复杂度O(n);如果初始的正好相反所有的记录按照关键字有序的序列的话此时是最坏的情况需进行n-1趟冒泡,比较的次数n(n-1)/2,移动的次数是3n(n-1)/2,时间复杂度O(n2)。冒泡排序的空间复杂度并不随着处理数据量n的大小而改变,为O(1)。 2.2选择排序 选择排序的基本思想是:选择排序的主要排序方式是通过选择进行完成的。在初始待排序的数据中找到最小的数据,并把它和初始数据中第一个位置的数据进行交换,同时在剩余的所有数据中按照相同的方法找到最小的数据与初始数据中第二个位置的数据进行比较,按照这种方式对余下的数据进行排序直到所有的数据排序完成,算法结束。 具体的排序过程如下所示: 1)在第一次排序过程中,从所有的m个数sort[0]-sort[m-1]中找到最小的数sort[i],并将sort[i]于sort[1]进行交换。 2)在第二次排序过程中,从剩余的sort[1]-sort[m-1]中再次找到最小的数sort[i],并将sort[i]于sort[2]进行交换。 3)在第j次排序过程中,从剩余的sort[j-1]-sort[m-1]中再次找到最小的数sort[i],并将sort[i]于sort[j-1]进行交换。 4)直到所有数据均有序,算法结束。 选择排序算法的程序如下所示: void paixu::selectsort(int r[],long m,long n) {for(i=m;i<=n-1;i++) {k=i; for(j=i+1;j<=n;j++) {if(r[j] temp=r[i]; //将r[k]和r[i]交换 r[i]=r[k];
r[k]=temp;}}
通过选择排序的代码可以看出,选择排序的执行过程是两个for循环的查找过程,第一个过程是查找最小元素,第二个过程是m次循环过程,所以时间复杂度是O(n2),所需进行的关键字间的比较次数是n(n-1)/2,移动记录的次数,最小值为0,最大值为3(n-1) 。选择排序的空间复杂度并不随着处理数据量n的大小而改变,为O(1)。
2.3插入排序
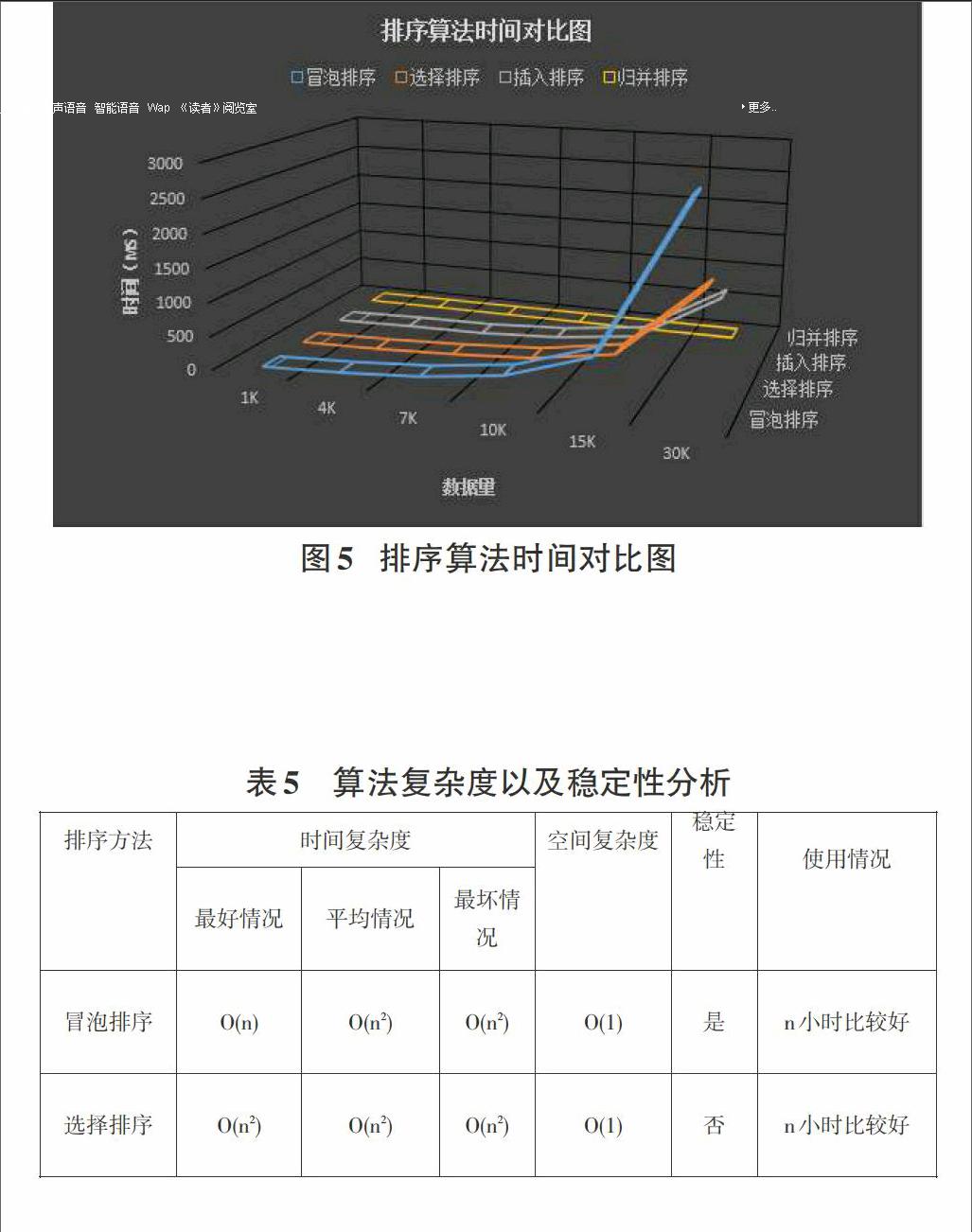
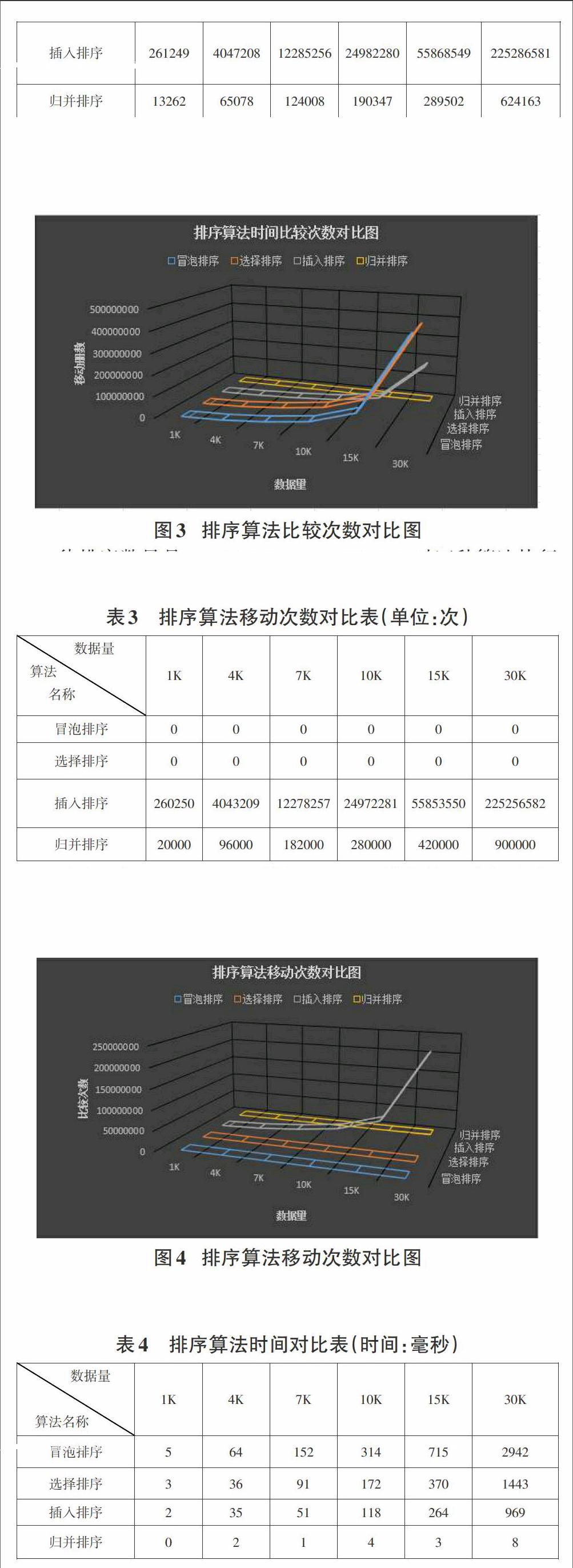
这里以希尔插入排序为例,希尔插入排序是对线性插入排序的一种改进,又称为缩小增量排序。希尔排序的基本思想是:对于一个记录数是m的待排序数据,首先选择一个增量dis1 具体的排序过程如下所示: 1)首先选取距离增量dis1,距离增量的初值小于记录数,之后以距离增量作为数据之间的距离,使得相同距离增量的数据分为同一组,并进行直接插入排序。 2)在上面排序结果的基础之后选择距离增量dis2,dis2增量的选取可以参照经典的二分法,向下取整二分dis1,按照步骤1的方式进行组内插入排序。 3)按照相同的距离增量选择原则进行排序直到距离增量为取值为1,此时相当于对一组数据进行直接插入排序,排序完成数据有序,算法结束。 希尔排序算法的程序如下所示: void paixu::shellsort(int r[],long m,long n) {gap=(n-m+1)/2; //增量的初值为n/2 while(gap>0) {for(i=gap+1;i<=n;i++) {j=i-gap; while(j>m-1) { if(r[j]>r[j+gap]) //交换r[j]和r[j+gap] {temp=r[j]; r[j]=r[j+gap]; r[j+gap]=temp; j=j-gap;} else j=m-1; //通过给j赋值而退出while循环}} gap=gap/2; //减小增量 }} 希尔排序是直接插入排序的改进,在性能上要优于直接插入排序。在希尔排序算法中如果初始的数据所有的记录按照关键字有序的序列的话此时是最好的情况,移动的次数为0,比较的次数在n~ n2之间;如果初始的数据所有的记录按照关键字逆序的序列的话此时是最坏的情况,移动次数和比较次数接近n2,但是在平均情况下希尔排序的比较次数和移动次数好于直接插入排序,为O(n1.3)左右。选择排序的空间复杂度并不随着处理数据量n的大小而改变,为O(1)。 2.4归并排序 归并排序采用的是分治思想,是将两个或多个有序序列合并成一个有序序列的过程。 具体的排序过程如下所示: 1)初始时,将每个记录看成一个单独的有序序列,则n个待排序记录就是n个长度为1的有序子序列; 2)对所有有序子序列进行两两归并,得到n/2个长度为2或1的有序子序列; 3)重复步骤2,直到得到长度为n的有序序列为止。 void paixu::sortmerge(int a[],long p1,long p2,int b[]) {//二路归并排序,将a[p1]~a[p2]中的元素排序,结果在b[0]~b[p2-p1]中 while(len {mmergesort(a,p1,p2,len,b); len=len*2; mmergesort(b,0,p2-p1,len,a+p1);}} void paixu::merge(int a[],long s,long m,long n,int b[]) {while(i<=m&&j<=n) { if(a[i]<=a[j])b[k++]=a[i++]; else b[k++]=a[j++];} while(i<=m){b[k++]=a[i++]; } while(j<=n){b[k++]=a[j++];} return;} 具有n个待排序记录的归并次数是㏒2n,而一趟归并的时间复杂度为O(n),则整个归并排序的时间复杂度无论是最好还是最坏情况均为O(n㏒2n)。在排序过程中,使用了辅助向量DR,大小与待排序记录空间相同,则空间复杂度为O(n)。归并排序是稳定的,归并排序的排序的空间复杂度和处理数据的规模n相关,为O(n)。 3实验验证 为了对比四种排序算法的性能,论文通过C++实现了一个验证程序。通过对比排序算法的交换次数、比较次数、移动次数以及排序时间来进一步分析算法性能。通过rand()函数模拟产生1000、4000、7000、10000、15000、30000不同规模的数据。 待排序数量是1K,4K,7K,10K,15K,30K时四种算法执行过程对应的交换次数如表1所示。 从表中可以看出插入排序以及归并排序并不进行交换,冒泡排序的交换次数规模是最大的,选择排序交换次数和算法数据规模基本相当。 待排序数量是1K,4K,7K,10K,15K,30K时四种算法执行过程进行的比较次数如表2所示。 从表2中可以看出冒泡排序以及选择排序的比较次数基本相同,插入排序以及归并排序的比较次数基本是比较少的。 待排序数量是1K,4K,7K,10K,15K,30K时四种算法执行过程进行的移动次数如表3所示。 从表3中可以看出冒泡排序以及选择排序并不进行移动,插入排序的移动次数规模是最大的,并且随着数据规模的增大增长速度也在变快,归并排序的移动次数相对较小。 待排序数量是1K,4K,7K,10K,15K,30K时四种算法执行过程进行的时间对比如表4所示。 从表4中可以看出当数据规模小于15K的时候,四种算法的耗时相对比较平稳,选择排序与插入排序耗时差别不大,冒泡排序相对较多,归并排序耗时相对其他三种算法不是一个数量级,数据规模大于15K时,归并排序的耗时基本变化不大,冒泡排序、选择排序以及插入排序的耗时成指数增长。 4性能分析 通过上述对冒泡排序、选择排序、插入排序以及归并排序算法的实验性能对比,并通过分析,列出表4.1中的性能对比。 其中整体来说在数据量比较大时归并算法的时间复杂度最低,但是以牺牲空间复杂度为代价的,插入排序和冒泡排序在数据初始正序时的时间复杂度较小,平均情况下插入排序和归并排序的时间复杂度较小,综上分析可以看出选择排序不稳定,冒泡排序、插入排序以及归并排序是稳定的。冒泡排序以及选择排序适合于数据量比较小的情况,归并排序适合数据量比较大的情况。 5结论 不同排序算法性能各有优劣,在选择排序算法时要综合排序算法的时间复杂度、空间复杂度、稳定性、适合的数据规模等各种因素。通过本文可以得出在数据量较大时选择归并排序,数据量较小时可以选择选择排序,数据大部分有序时可以选择插入排序。 由于本文只对冒泡排序、选择排序、插入排序以及归并排序四种典型的排序算法进行分析讨论,从而有一定的局限性,后续应对更多排序算法的性能进行分析比较。 参考文献: [1] 严蔚敏,吴伟民.数据结构[M].北京:清华大学出版社,1997:263-289. [2] 王晓东.计算机算法设计与分析[M].北京:电子工业出版社,2007:21-25.

