近岸波浪数值计算中两种动边界处理的比较
汪鸿,李训强,朱首贤,唐建,聂屿
(1.解放军理工大学气象海洋学院 南京 211101;2.河海大学海洋学院 南京 210098;3.海军南海舰队 湛江 524000)
近岸波浪数值计算中两种动边界处理的比较
汪鸿1,李训强1,朱首贤2,唐建3,聂屿1
(1.解放军理工大学气象海洋学院 南京 211101;2.河海大学海洋学院 南京 210098;3.海军南海舰队 湛江 524000)
在近岸波浪数值计算中,动边界处理是不可避免的问题。文章基于Boussinesq方程的FUNWAVE-TVD模式,引入窄缝法对波浪水槽实验进行数值模拟,比较窄缝法和干湿网格法的波浪数值计算结果;设计多种周期和波高的波浪数值试验,分析两种动边界处理下数值计算结果的差异。结果表明,两种动边界处理对近岸波浪破碎的数值模拟有影响,对波浪漫滩区的计算影响尤为显著。
动边界处理;波浪破碎;波浪漫滩;海洋动力学;数值模拟
1 引言
波浪在由深水向浅水传播过程中,由于水深变小,波陡不断增大至极限,导致波浪发生倒卷和坍塌的现象,称为波浪破碎[1-2]。波浪在破碎后向岸继续传播时,水陆分界线随波峰向岸推进、随波谷向海回退,在一个波动周期中滩地出现被海水淹没和露出水面的过程,称为波浪漫滩[3]。波浪漫滩的上界为波浪向岸爬高的最高位置,下界为波浪向海回退的最低位置,上界和下界之间的区域称为波浪漫滩区。随着科学技术的发展,人类对海洋资源的开发与利用显著增加[4-5],近岸海洋工程的建造与维护以及人员近岸活动需求也日益增多[6],近岸海洋活动和工程建筑的安全保障成为较为突出的问题。近年的很多研究表明,波浪破碎是近岸区域波浪运动最为剧烈的物理过程,其对波浪预警预报以及近岸岛礁的船只航行、工程建设和资源补给具有重要的安全威胁,因而一直受到广泛关注[7-8]。近岸波浪破碎带和波浪漫滩对近岸水动力有重要影响,是近岸泥沙运输的两个峰值区,是海滩泥沙侵蚀、搬运和地貌演变的重要机制[9-11]。一些研究表明,波浪漫滩区的泥沙输运有时可占整个近岸区域沿岸方向泥沙输运的50%[12-13]。深入研究近岸波浪演变有利于提高近岸波浪预警和保障水平,对维护近岸人员生命财产和国防安全具有重要意义。
数值计算是研究波浪近岸演变的重要手段,目前主要采用Boussinesq方程[14]和非线性浅水方程[15]进行近岸波浪的数值模拟研究。该类方程通过描述波动过程的水质点运动来计算波浪,一般要求网格步长远小于波长、时间步长远小于波动周期,计算量庞大,适用于计算小范围、短时间的波浪运动问题。这类模型在计算过程中,水陆间的动边界处理是不可避免的问题,有些模型直接忽略近岸水线的移动,采用在一定水深处设置固壁的方法简化处理边界移动过程,而更多的波动质点类模型采用的是干湿网格法[16-17]和窄缝法[18]处理波浪数值模拟过程中的动边界问题。在干湿网格法计算时,随着水陆交接位置的变化不断更新计算边界,并对有水区域重新进行网格划分;该方法在计算中需要不断重新划分网格,机时耗费太大,在重新划分网格时还容易出现病态的网格。Tao等[19]结合实际海岸中部分水体渗入滩地的情况提出窄缝法以处理近岸移动边界,假设岸滩内存在水流可以通过的窄缝,从而将动边界区域转化为始终有水的计算区域;该方法显著提高计算效率,但是窄缝的存在造成波浪水体质量和能量的损耗,这些效应对波浪计算的影响一直备受关注,也有学者做了大量工作[18]。对两种动边界处理下近岸波浪数值计算的差异进行研究很有意义但比较少见,本文采用Boussinesq方程的FUNWAVE-TVD模式,分别引入窄缝法和干湿网格法,对近岸波浪数值计算结果进行比较和分析。
2 近岸波浪数值计算的动边界处理
FUNWAVE-TVD模式是美国Delaware大学基于完全非线性Boussinesq方程建立的,该模式处理动边界过程采用的是干湿网格法,对近岸附近的波浪传播及演变具有较好的模拟效果[20],但计算机时耗费较大。对于FUNWAVE-TVD模式的方程和处理有不少文献介绍,本文不再赘述[14]。
窄缝法是目前处理动边界的另一种主要方法,该方法把整个计算区域作为具有窄缝或可渗透的海床,把固体海底假设成具有窄缝或渗透边界的活动型区域,使溢出的水位不会超过海滩高程(图1)。Madsen等采用窄缝法对Carrier和Greenspan的理论模型进行数值模拟,发现其最大波高与理论解存在10%的误差[21]。

图1 窄缝法示意
引入窄缝法时,窄缝的控制参数为:
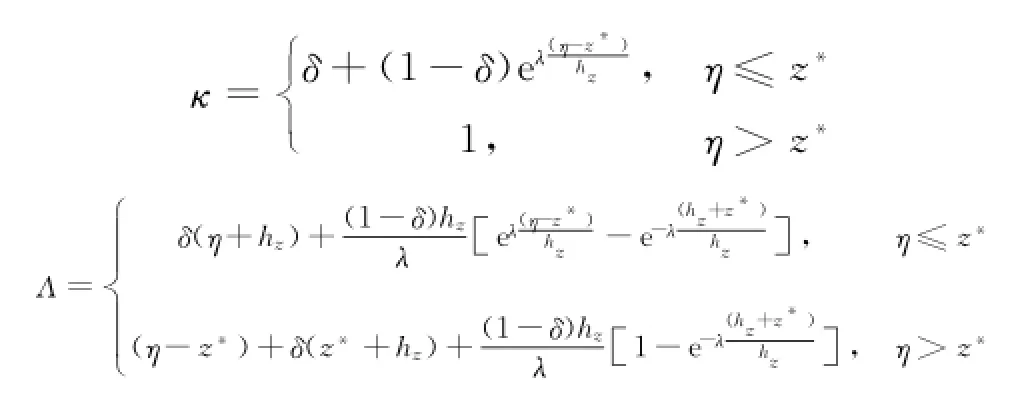
式中:κ为单位宽度上的窄缝宽;δ为最小缝宽;λ为窄缝的形状参数;hz为窄缝起始的水深值;Λ为考虑窄缝影响后的等效水深;η为波面水位。本文引入窄缝法时,z*取为:

式中:zs为陆地高程。
3 近岸波浪数值计算结果比较
Hansen和Svendsen设计一组规则波在斜坡地形上传播的水槽实验[14]。水槽左边的平底水深为0.36 m,右侧斜坡坡度为Slope=0.029 2,波浪的入射波高H=4.3 cm、周期T=3.33 s。实验主要测量波浪在斜坡上浅化传播的波高变化(图2)。
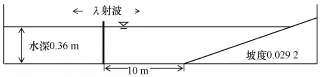
图2 数值地形设置
本文采用FUNWAVE-TVD模式对Hansen和Svendsen的波浪水槽实验进行数值模拟,数值模式的地形配置与波浪水槽实验完全相同。造波源函数采用双向造波法,造波源左端设置宽为1 m的海绵消波层以实现无反射造波,造波区位于斜坡左侧10 m远处。数值模型的网格距离为0.025 m× 0.10 m,时间步长为0.01 s。分别采用窄缝法和干湿网格法对波浪的动边界进行处理。本文中窄缝形状过渡参数为λ=20,窄缝宽度为δ=0.01 m,窄缝起始水深为hz=0.2 m,干湿网格判断的临界水深为0.001 m。模式计算20 s后,波面呈现很有规律的变化,波浪的波高基本保持稳定。
将数值模式稳定后30 s内平均的波高模拟值与观测数据比较,窄缝法和干湿网格法条件下的波高计算结果和实验测量结果如图3所示,其中横轴为不同测点位置的水深,纵轴为各水深处波浪平均波高,“*”为数值计算的波浪破碎位置。结果表明,采用窄缝法和干湿网格法对FUNWAVE数值模型模拟波浪破碎的影响不大,即在两种动边界处理下,模型都能模拟出波浪由于地形浅化作用在近岸区域发生堆积并破碎的现象。波浪的波陡是波浪破碎的关键指标,在实验测量数据中波浪破碎处波陡为0.029 6,采用干湿网格法和窄缝法计算的破碎波陡偏小,分别为0.027 3和0.024 5,证明计算的波浪破碎位置提前。在离岸较远的区域,动边界处理对波浪波高计算结果影响不大,随着离岸距离的减小,波高的计算差异逐渐增大,在波浪破碎区和漫滩区波高模拟的差异尤其显著。与干湿网格法计算结果比较,采用窄缝法处理动边界下模拟的破碎位置前移,而破碎波高相对减小,计算的波浪在破碎区后波高也偏小,这种差异可能是由于窄缝的存在,在波浪向岸传播过程中首先要填满窄缝,从而引起水体质量的损失并导致波浪能量的衰减,使波浪的破碎提前、破碎波高减小。与实验数据比较,采用窄缝法和干湿网格法计算得到的最大波高分别减小0.82 cm和0.70 cm,破碎水深分别增大0.021 m和0.007 m;采用干湿网格法计算的破碎波高和破碎位置与实验观测结果更为符合,但波浪破碎后的计算波高显著大于实测值。此外,与实验数据相比,图3中FUNWAVE模式波高的计算结果在破碎前偏大而破碎处偏小,Shi[14]和Kennedy[22]在采用Boussinesq方程计算波浪破碎时也出现破碎波高偏小的结果,Shi在模拟中提出该误差是由于Boussinesq模型的网格数值耗散导致的[14]。

图3 两种动边界下波高计算结果
波浪漫滩是近岸波浪运动的小尺度过程,水体的质量和水质点能量的变化对波浪漫滩过程的影响更为明显。本文在FUNWAVE模式中采用窄缝法和干湿网格法处理Hansen和Svendsen实验,分别计算波浪爬高的最高位置xh和回落的最低位置xl。采用窄缝法和干湿网格法处理动边界,波浪最高和最低位置时水槽中波浪的瞬时水位如图4所示。可知,采用窄缝法计算的波浪爬高最高位置xh相对干湿网格法计算的xh偏低,而波浪回落最低位置xl则相差不大,很明显是由于窄缝的存在,波浪在向岸爬升过程中水体的损失和能量的耗散导致的;图4(a)中,由于窄缝的存在,在斜坡内部仍然存在较小的水质点波动,对波浪破碎后能量的损耗有明显作用,这与实际观测是较为相符的。

图4 漫滩上下界位置两种边界计算水位分布
由于Hansen和Svendsen的实验中没有对波浪漫滩区进行观测,本文采用目前工程应用计算规则波爬高最多的Hunt经验公式计算Hansen实验的爬高位置。Hunt公式为:

式中:R为波浪爬高的垂直距离;T和H分别为波浪入射周期和波高;β为坡度角。
计算Hansen实验爬高位置所需的参数易由实验条件得到。Hunt公式计算的爬高最大位置R= 0.237 m,转化为沿波浪传播方向上,波浪爬高区长为0.863 m。两种动边界处理得到的漫滩区范围与Hunt经验公式结果的比较如表1所示,采用窄缝法和干湿网格法计算的波浪爬高区分别长0.675 m和1.30 m,与Hunt公式计算结果相比,波浪爬高区分别相差0.188 m和0.437 m,以Hunt公式计算结果为准的相对误差分别为21.78%和50.64%,采用窄缝法计算误差更小;结合图3中波高的计算结果,这是干湿网格法在近岸漫滩区附近波高显著偏大造成的。
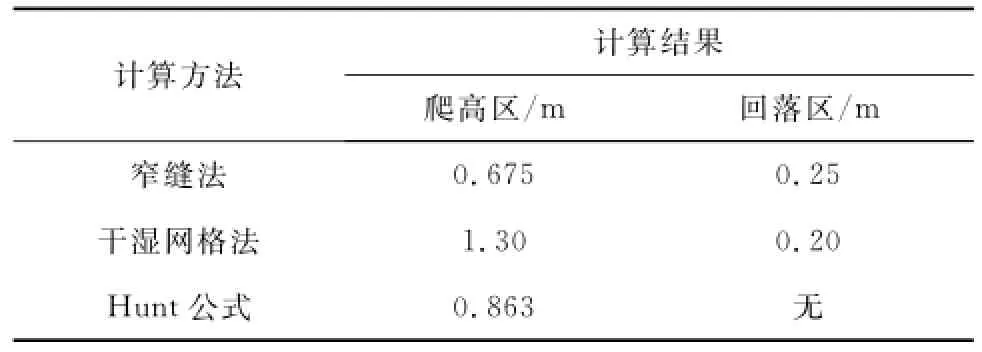
表1 Hansen实验漫滩区计算比较
4 不同入射条件下动边界处理对波浪漫滩计算的影响
一般而言,波浪的入射波高和周期对波浪漫滩区的分布有较大影响。本文通过改变上述实验的波高和周期,以Hunt公式计算的波浪爬高距离为标准,分别统计窄缝法和干湿网格法处理下不同入射条件得到的波浪爬高位置,并计算其与Hunt公式计算的爬高距离的相对误差(表2和表3)。由于Hunt公式仅能计算波浪爬高位置,本文未讨论两种动边界处理的波浪回落位置差异。

表2 入射周期不变(T=3.33 s)的波浪爬高
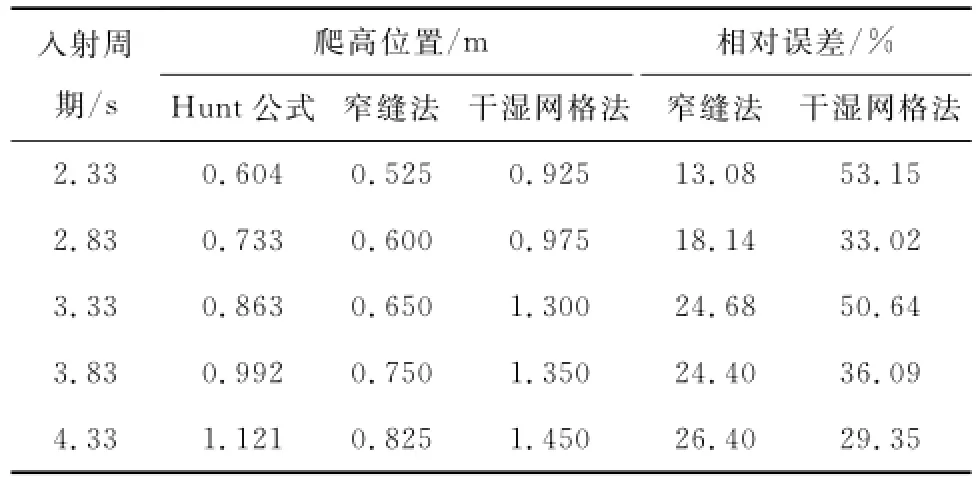
表3 入射波高不变(H=4.3 cm)的波浪爬高
表2保持波浪入射周期T=3.33 s不变,仅改变波浪入射波高;表3保持波浪入射波高H=4.3 cm不变,仅改变波浪周期。Hunt公式计算结果表明,随着波浪波高和周期的增大,波浪的爬高距离随之增加,采用窄缝法和干湿网格法都能较好地模拟出这种变化趋势;由不同入射条件下两种动边界处理的爬高位置与Hunt公式计算结果的相对误差可以发现,在本文选取的多种波浪入射条件下,采用窄缝法处理的爬高误差显著小于采用干湿网格法处理的爬高误差,且窄缝法处理的相对误差保持在20%左右,而干湿网格法处理的相对误差变化较大。
5 结论
本文采用FUNWAVE-TVD模式对Hansen水槽实验进行数值模拟,结果表明采用不同动边界处理对近岸波浪破碎区的计算有较大差异。采用窄缝法计算的波浪破碎波高偏小且破碎位置相对前移,该法不仅能减少模型计算机时消耗,而且对波浪漫滩区计算的准确性也有一定的提高;对多种入射波高和周期条件下波浪爬高的计算结果进行比较,结果表明采用窄缝法处理与经验公式的相对误差更小。在以后的工作中要加强对波浪爬高的现场观测,通过数值模拟与实测资料的对比,进一步分析两种动边界处理对近岸波浪数值计算的影响。
[1]CHEN Qin,KIRBY J T,DALRYMPLE R A,et al.Boussineso modeling of wave transformation,breaking,and runup.II:2D[J].Journal of Waterway Port Coastal& Ocean Engineering,2014,126(1):39-47.
[2]QIN C,KIRBY J T,DALRYMPLE R A,et al.Boussinesq modeling of longshore currents[J].Journal of Geophysical Research,2003,108(C11):211-227.
[3]PULEO J A,BUTT T.The first international workshop on swash-zone processes[J].Continental Shelf Research,2006,26(5):556-560.
[4]郑崇伟,潘静,孙威,等.经略21世纪海上丝路之海洋环境特征系列研究[J].海洋开发与管理,2015,32(7):4-9.
[5]郑崇伟,李训强,高占胜,等.经略21世纪海上丝路之海洋环境特征:风候统计分析[J].海洋开发与管理,2015,32(8):4-11.
[6]郑崇伟,李崇银.中国南海岛礁建设:风力发电、海浪发电[J].中国海洋大学学报:自然科学版,2015,46(9):7-14.
[7]郑崇伟,潘静,黎鑫,等.1988-2009年中国海及周边海域大浪频率对ElNino的响应[J].海洋通报,2014(2):140-147.
[8]ABADIE S C,GANDON S,GRILLI R,et al.3D numerical simulations of waves generated by subaerial mass failures:Application to La Palma case[C]//Proceedings of the 31st International Coastal Engineering Conference.Singapore:World Sci.,2008:1384-1395.
[9]HORN D P.Measurements and modelling of beach groundwater flow in the swash-zone:a review[J].Continental Shelf Research,2006,26(5):622-652.
[10]MASSELIND G,PULEO J A.Swash-zone morphodynamics[J].Continental Shelf Research,2006,26(5):661-680.
[11]BROCCHINI M.Integral swash-zone models[J].Continental Shelf Research,2006,26(5):653-660.
[12]WELLEN E V,BALDOCK T,Chadwick A,et al.STRAND:A Model for Longshore Sediment Transport in the Swash Zone[C].Proceedings of the 27th International Conference on Coastal Engineering.Sydney:Coastal Engineering,2001:3139 -3150.
[13]Elfrink B,Baldock T.Hydrodynamics and sediment transport in the swash zone:a review and perspectives[J].Coastal Engineering,2002,45(3):149-167.
[14]SHI F,KIRBY J T,HARRIS J C,et al.A high-order adaptive time-stepping TVD solver for Boussinesq modeling of breaking waves and coastal inundation[J].Ocean Modelling,2012,43-44(2):36-51.
[15]BROCCHINI M,PEREGRINE D H.Integral flow properties of the swash zone and averaging[J].Journal of Fluid Mechanics,1996,317(1):241-273.
[16]张文静,朱首贤,黄韦艮.卫星遥感资料在湛江港风暴潮漫滩计算中的应用[J].解放军理工大学学报:自然科学版,2009,10(5):501-506.
[17]吕新刚,乔方利,夏长水.胶州湾潮汐潮流动边界数值模拟[J].海洋学报,2008,30(4):21-29.
[18]陶建华.波浪在岸滩上的爬高和破碎的数学模拟[J].海洋学报,1984,6(5):692-700.
[19]TAO Jianhua,LI Qingxue,FALCONER R A,et al.Modelling and assessment ofwaterquality indicators in a semi-enclosed shallow bay[J].Journal of Hydraulic Research,2001(6):611-617.
[20]CHOI J,KIRBY J T,YOON S B.Boussinesq modeling of longshore currents in the Sandy Duck experiment under directional random wave conditions[J].Coastal Engineering,2015,101:17-34.
[21]CARRIER G F,GREENSPAN H P.Water waves of finite amplitude on a sloping beach[J].Journal of Fluid Mechanics,1958,4(1):97-109.
[22]KENNEDY B,CHEN Q,KIRBY J T,et al.Boussinesq modeling of wave transformation,breaking,and runup I:1D[J]. Journal of Waterway Port Coastal &Ocean Engineering,2002,126(1):39-47.
Comparison of Two Moving Shoreline Handling Method Results in near-Shore Wave Calculation
WANG Hong1,LI Xunqiang1,ZHU Shouxian2,TANG Jian3,NIE Yu1
(1.PLA University of Science and Technology,Nanjing 211101,China;2.Institute of marine,Hohai University,Nanjing 210098,China;3.Naval Nanhai fleets of PLA,Zhanjiang 524000,China)
Moving shoreline is an inevitable issue in numerical calculation nearing the surf zone. This paper laid slot method to the fully nonlinear Boussinesq model FUNWAVE-TVD to simulate flume experiment,then compared with the numerical result of slot and wet-dry method.Besides,series numerical calculations were designed to analyze the result of two shoreline handling method.The results showed that the impact of moving shoreline on wave shoaling and breaking calculation is obvious close,especially in the calculation of swash zone.
Moving-shoreline,Wave breaking,Swash,Ocean dynamics,Numerical simulation
P731
A
1005-9857(2016)09-0094-05
2016-04-11;
2016-07-25
国家自然科学基金(41206163,41376012,41076048);中央高校基本科研业务费项目(2011B05714,2014B06514).
汪鸿,硕士研究生,研究方向为海洋动力学与数值模拟,电子信箱:wanghong_92@126.com
李训强,副教授,硕士,研究方向为海洋动力学与数值模拟,电子信箱:lixunqaing@sina.com

