乳山震群震源谱参数的稳健反演

郑建常，王鹏，徐长朋，许崇涛，刘凯，李冬梅，李翠芹

1 山东省地震局，济南 2500142 五莲地震台，山东五莲 2623003 德州地震台，山东德州 253000



乳山震群震源谱参数的稳健反演

郑建常1，王鹏1，徐长朋1，许崇涛2，刘凯3，李冬梅1，李翠芹1

1 山东省地震局，济南 2500142 五莲地震台，山东五莲 2623003 德州地震台，山东德州 253000

本文引入截止频率fmax提出基于Brune模型的高频截止(High-Cut)模型，采用两步反演的方法来拟合求解震源谱的特征参数，并给出其误差范围；实际应用显示该模型的理论谱对观测谱有很好的拟合，可明显改善拐角频率识别的准确度.将该方法应用于2013—2015年的乳山震群，计算了乳山震群25次ML≥3.0事件的震源参数(地震矩、破裂半径、应力降等)，进一步对乳山震群的震源破裂特性进行了讨论.结果显示：拐角频率、应力降与震源尺度大小明显相关；高频衰减系数γ与震源破裂区的复杂程度以及破裂性质有关，当观测记录中混杂有其他事件的波形或微破裂时，高频衰减系数大于2，并且不确定性增大；截止频率fmax与地震大小存在一定相关性；使用Beresnev(2001)给出的震源半径计算公式，得到的乳山震群的结果显示与华北地区的经验关系较为一致；乳山震群的应力降明显偏小(最大不超过0.15 MPa)，一方面反映了震中区域的构造应力水平，另一方面可能还意味着此次震群是一个相对非耗散型的脆性破裂过程，属于低摩擦应力的断层作用.

震源参数；拐角频率；破裂半径；应力降；高频衰减系数

1 引言

根据台站记录波形的振幅谱反演求解地震事件的震源参数，在目前已经逐渐成为地震学中的日常工作；很多情况下，基于经典Brune模型由观测谱拟合得到的诸如应力降、视应力、破裂半径等参数在大震危险性估计、震后趋势判定方面有着重要的应用(如：Choy and Kirby,2004；易桂喜等，2011)，并且可以根据这些参数估计和分析断层的运动学和动力学特征(如：Jones and Helmberger,1998；周仕勇和许忠淮，2000；Stankova-Pursley et al.,2011).

由观测谱求解震源参数的工作自20世纪70年代Brune等给出理论解释(Brune,1970,1971;Hanks and Wyss,1972)并开始用于应用研究(陈运泰等，1976)；数十年来，随着数字地震仪的广泛布设，这项工作在全球范围内得到了广泛的开展(Sereno et al.,1988;秦嘉政等,2003;Shearer et al.,2006;Tusa et al.,2006;Allmann and Shearer,2009;赵翠萍等,2011;Lancieri et al.,2012;Zollo et al.,2014;Goebel et al.,2015)，震源谱参数的反演理论和方法也得到了长足的进展(Andrews,1986;Atkinson,1993;Moya et al.,2000;Izutani and Kanamori,2001;Baltay et al.,2013;Kaneko and Shearer,2015).

但是，伴随着这些进展，有关震源参数的反演仍存在很多争议(Ide and Beroza,2001；Beresnev,2001,2002,2009).

首先，从频谱图上，拐角频率一般很难测准(吴忠良，2003)；并且由于理论震源谱是简化的理想化模型，只有零频极值和拐角频率两个参数，自由度很低；更进一步，在由震源谱导出一些物理参数时，使用了许多经验的估计值以及经验关系(典型的如Brune(1970)给出的ωC=2.34×VS/R(VS为横波速度，R为破裂半径)，对这一系数不同的学者给出了不同的值，参见Kaneko和Shearer(2014，2015)的讨论和数值实验)，由于真实破裂过程的复杂性和不同震源模型的抽象化，很难说清这些参数本身的可靠性和可信度究竟有多大.有鉴于此，Kane等(2011)使用经验格林函数和小孔径台阵资料给出了震源谱参数不确定性的量化估计，Baltay等(2013)提出了基于波形记录谱的稳健应力降计算方法.

其次，本质上这些震源参数都基于震源谱的零频极值和拐角频率两个特征，这些参数之间通常不是相互独立的(吴忠良，2003)，大量的研究结果也显示诸多的波谱参数之间存在着明显的相关关系(Lyskova et al.,1998;张天中等，2000；Wu,2001；Drouet et al.,2005;Izutani,2008).Beresnev(2001，2002)通过理论分析认为，拐角频率和震源半径之间的关系从本质上是不清楚的，因此无法通过震源谱准确地确定震源尺度.

此外，在地面运动的加速度谱中，广泛地观测到频谱的另一个特征参数：频率上限(或截止频率)fmax，该参数究竟来源于震源过程或者由于地壳或近地表的高频辐射衰减和散射，目前尚没有统一的意见.一部分学者认为fmax是场地效应而不是震源破裂过程属性(如：Hauksson et al.，1987；Frankel，1995)，而更多的学者认为fmax与场地无关(如：Papageorgiou and Aki，1983；Papageorgiou，1988).Papageorgiou和Aki(1983)考虑了震源障碍体模型的特殊情形，通过分析推测fmax很可能来自于断层的非弹性，并认为与断层的黏合区的大小成反比.Iwakiri和Hoshiba(2012)使用ω2和fmax模型研究发现2011年日本“311”大地震的开始50 s波形中存在显著的10 Hz以上的高频成分，他们分析认为来自更深部区域的辐射可能是高频运动的主要原因.Wen和Chen(2012)通过强地面运动记录计算了汶川地震的频率上限fmax，结果显示fmax反映了震源复杂的破裂过程.

本文中，我们引入频率上限fmax给出了基于Brune模型的高频截止(High-Cut)模型，由此来拟合求解地震的谱参数和计算震源参数.在实际计算过程中，采用两步反演的方法，使用粒子群算法来稳健地获取震源谱的特征参数(零频极值、拐角频率、高频衰减系数、截止频率以及截止频率之上的衰减系数)，并给出其误差范围.最后将该方法应用于2013年活动至今的乳山震群，并基于相对可靠的震源谱参数计算乳山震群ML≥3.0事件的震源参数(地震矩、破裂半径、应力降等)，进一步对乳山震群的震源破裂特性进行了讨论.

由于在自相似的假设和Brune模型下，应力降与视应力存在成比例的线性对应关系(Singh and Ordaz,1994;Baltay et al.,2011)，因此本文中我们不再讨论视应力的问题.

2 理论与方法

2.1 震源谱理论

客观地，从震源谱中我们可以得到四个参数：零频极值Ω0、拐角频率fC、高频衰减系数γ以及频率上限(截止频率)fmax(陈运泰等，2000).但在日常的地震频谱分析和震源参数反演中，绝大多数的工作只考虑了前两项.在理论上，高频端的震源谱Ω(ω)以ω-γ的形式衰减(陈运泰等，2000)

(1)

式中，高频衰减系数γ被认为是与破裂的运动学性质有关的常数.

一次大的破裂往往是很多尺度更小的小破裂组成的，考虑这些小破裂遵循自相似原则，且定义断层面的分形维为D.则(陈运泰等，2000，公式5.232)

(2)

其中，η为Hurst指数.假定断层面上的应力降的随机起伏满足布朗运动分布，且应力降超出平均水平部分为“小地震”，则D=2-η，显然经典的Brune模型中，破裂面被理想化为圆盘状，分形维D=2，因此高频衰减系数γ也就被固定为2.

(3)

Brune模型提出后，在面向中小地震的研究应用中得到了极大的成功，当前在很多地震研究机构，根据Brune模型求解震源参数已经成为例行的工作内容(刘杰等，2003；华卫等，2009；王鹏和郑建常，2014).但正如我们在引言中所说，在实际的应用中，无论是理论谱的程序拟合或者手动选择，拐角频率的准确测定是很困难的.

关于震源谱，存在不同的理论模型(Atkinson and Boore，1998；Boore et al.，2014).为了解释台站观测到的加速度谱中截止频率之上的高频成分快速衰减的现象，Boore(1983)提出了高频截止模型.设ω为角频率，定义加速度谱A(ω)为(Boore，1983，公式(1))：

(4)

其中，R为圆盘模型的震源破裂半径，Q为介质品质因子，C为常数，

(5)

式中，Rθ φ为辐射因子，FS为自由表面的放大效应，PH为解释能量分解到两个水平分量的因子，ρ为介质密度，β为剪切波速度.公式(4)中S(ω)为典型的Brune模型震源谱，

(6)

其中ωC为角频率形式的拐角频率.P(ω)为与高频截止频率ωmax有关的高频衰减模型，

(7)

理论模拟和数值试验显示该模型可以很好地解释加速度观测谱(Boore，1983,2003；Boore et al.,1997).

参考Boore(1983)对高频地面运动的模拟，我们对中小地震，定义位移谱

(8)

式中，Ω0为零频极值，p为高于截止频率fmax部分的频谱衰减系数.在该模型中，充分考虑了理论震源谱的四个参数，或许可以更进一步地提高我们对震源过程的认识.

2.2 反演方法

根据前面所述的理论模型，我们采用了两步反演的方法.

在反演之前，台站记录经过去趋势、去均值，扣除仪器响应、消除几何衰减效应后，旋转到Z-R-T坐标系，根据台网观测报告的各个台站P、S到时按照到时关系法截取S波段，使用SH波进行分析.对观测数据进行余弦边瓣加窗，使用快速傅里叶变换得到观测谱.

首先，由至少4个以上的台站观测谱得到平均震源谱，由于一般测震台的地震仪均为速度计，将速度谱分别经过积分和微分得到位移谱和加速度谱，取最大速度谱值作为拐角频率fC初始值，最大加速度谱值对应的频率作为频率上限fmax的初始值.

反演过程中，第一步先使用初始fmax之内的频谱部分，设公式(8)中的γ=2，对其进行拟合，得到拐角频率值；第二步，使用该拐角频率值之后的高频部分，对公式(8)进行拟合，得到截止频率值；最后，取拐角频率和截止频率之间的频谱部分，以稳健回归的方法确定高频衰减系数γ的值.

在震源谱参数反演中通常使用的方法是对傅里叶谱的最小二乘拟合(Lindley and Archuleta，1992)，在本文的两步反演过程中，我们使用粒子群算法(郑建常和陈运泰，2012；郑建常等，2013，2015a)拟合公式(8)表示的理论谱，并进一步估计各项待求参数的95%置信区间，最后给出理论谱的95%置信范围(图1b)，这里确定95%置信区间时使用的是基于参数估计的渐进正态分布方法(Bates and Watts,1988).图2给出了2013年10月1日乳山ML3.8事件的例子，分别展示了位移和加速度的平均观测谱以及反演得到的高频截止模型的理论谱，可见理论谱对观测谱有很好的拟合效果.

2.3 震源参数

由震源谱本身的拐角频率、零频极值参数，可以进一步导出震源半径R、应力降Δσ等震源参数.在经典的Brune模型中，

(9)

图1 2013年10月1日乳山ML3.8地震位移谱(a)和加速度谱(b)拟合结果Fig.1 Theoretic (blue) and observed (magenta) spectra of displacement (a) and acceleration (b) of Oct.1,2013 ML3.8 Rushan event

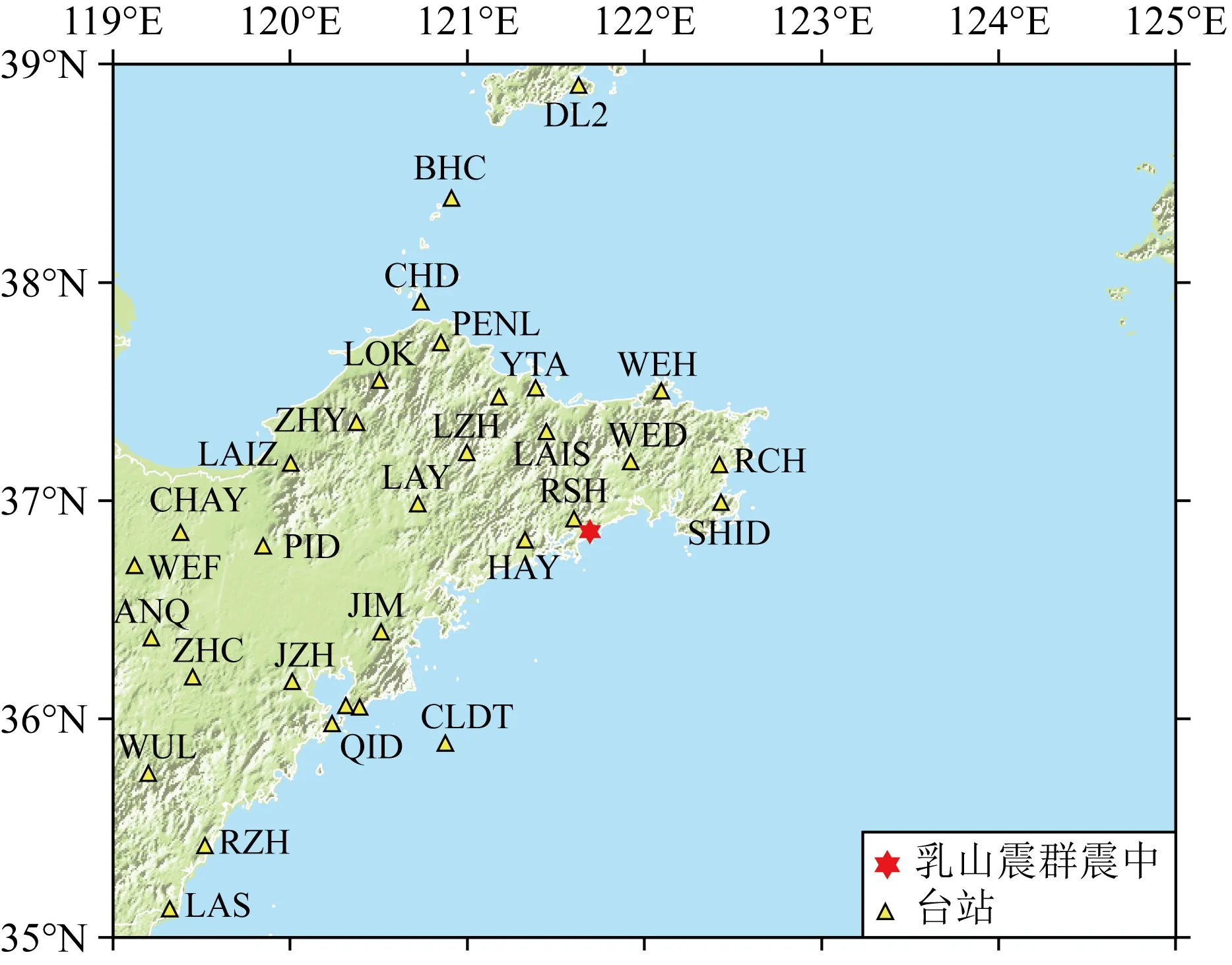
图2 乳山震群震中区及胶东半岛地区台站分布图Fig.2 Map showing locations of seismic stations (triangles) in Jiaodong Peninsula and the Rushan swarm (hexagram)

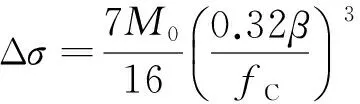
(10)

其中，M0为标量地震矩.

Beresnev(2001)经过讨论给出了更加合理的震源尺度与拐角频率之间的关系式：

(11)

式中，VR为破裂传播速度，L为断层破裂长度.式中“≈”是由于取VR≈0.8β(观测资料和大量研究显示，断层的破裂速度一般为剪切波速度的0.7～0.9倍).在本文中，我们依据公式(11)来计算破裂半径(对比公式(9)和公式(11)，两个关系式给出的震源半径相差约3.5倍).

3 数据与资料

乳山震群自2013年10月1日开始活动，截至2015年底，共记录到地震事件超过1万次，其中ML≥3.0有28次，最大为2015年5月22日4.6级地震.震中距200 km范围内有山东测震台网的固定台19个(图2)，另外如LAIS、PENL、CHAY等隶属于市地震局台网，SHID、CLDT、ZHCT等为山东局“十二五”项目建设，这些台在2014—2015年先后纳入山东台网.考虑到观测数据的连续性以及信噪比情况，我们选择了震中距150 km以内的HAY、LAY、LZH、YTA、WED、WEH、RCH、ZHY、LOK、QID、CHD等11个台的资料进行分析，RSH台震中过近(12 km)，因此没有选用.在扣除非弹性衰减效应的过程中，使用了石玉燕等(2008)给出的山东地区的研究结果：

(12)

4 结果分析

我们共反演了乳山震群25次ML≥3.0级地震的震源谱，结果见图3，并计算给出了这些震源谱的参数(表1).

4.1 拐角频率

拐角频率实际上是反映震源尺度大小的物理量，诸多的研究也发现，拐角频率和地震矩、震级之间存在相关关系(Lyskova et al.,1998;张天中等，2000；Drouet et al.,2005;Izutani,2008).从我们反演得到的结果也可以发现有较好的相关性(图4). 图5a给出了乳山震群拐角频率值随时间的变化曲线，并且给出了反演的fC值的不确定性范围.

图3 乳山震群25次ML≥3.0级地震位移谱拟合结果Fig.3 Theoretic (solid blue line) and observed (magenta) displacement spectra of 25 ML≥3.0 events of the Rushan swarm

发震时间yyyy-mm-ddHH:MM:SS震级MLMW地震矩M0(N·m)拐角频率fC(Hz)衰减系数γ截止频率fmax(Hz)p破裂半径R(m)应力降Eq.(9)Eq.(11)σ(MPa)2013-10-0112∶07∶553.83.237.711×10131.037±0.1142.224±0.08616.765±0.7392.6101256.9359.90.0172013-10-0511∶30∶023.22.414.559×10122.290±0.3962.146±0.11716.110±0.5942.553569.2163.00.0112013-12-0913∶38∶033.22.661.110×10131.543±0.2432.190±0.07912.276±0.8951.467844.6241.80.0082014-01-0722∶24∶074.73.633.163×10141.285±0.2492.460±0.69311.636±0.7531.4831014.7290.50.1322014-01-0916∶54∶303.52.641.036×10132.102±0.2612.255±0.11916.493±0.9361.847620.2177.60.0192014-02-2501∶50∶033.52.781.677×10131.465±0.3572.275±0.08716.883±0.4963.376889.9254.80.0102014-02-2505∶23∶013.52.721.357×10131.612±0.2761.922±0.33012.081±0.6271.918808.7231.60.0112014-02-2505∶23∶273.52.731.389×10131.686±0.4021.527±0.28111.974±0.6593.106773.3221.40.0132014-04-0400∶12∶164.43.561.764×10140.991±0.0922.185±0.13110.787±0.6823.4961315.7376.70.0342014-05-1821∶20∶013.02.313.279×10121.118±0.1131.887±0.10817.896±1.0884.9531166.0333.90.0012014-07-1600∶40∶243.52.801.770×10131.235±0.0681.707±0.20716.648±2.9193.3121055.8302.30.0072014-09-0309∶08∶353.42.547.320×10121.216±0.1611.572±0.51710.638±0.7124.3741071.8306.90.0032014-09-0309∶47∶223.22.465.498×10122.097±0.3712.154±0.17718.406±1.7552.176621.6178.00.0102014-09-0310∶25∶373.02.516.466×10121.261±0.4861.550±0.45012.648±0.5195.1831033.7296.00.0032014-09-0310∶30∶483.42.455.348×10121.347±0.0411.682±0.25918.504±3.4803.530967.3277.00.0032014-09-1614∶42∶584.13.227.461×10131.361±0.1271.892±0.24510.984±3.1482.465957.6274.20.0372014-09-1614∶43∶333.92.983.341×10131.551±0.1102.065±0.11013.488±0.5725.859840.2240.60.0252014-11-0607∶57∶293.12.363.870×10121.332±0.1631.643±0.18817.158±0.7823.682978.6280.20.0022014-12-1302∶03∶283.32.465.448×10121.680±0.1312.023±0.11218.691±1.0484.937776.0222.20.0052015-05-2200∶05∶324.83.981.040×10150.698±0.0491.958±0.18912.156±3.5522.4721867.8534.80.0702015-06-0922∶29∶083.72.791.711×10131.299±0.1211.966±0.14319.271±0.9103.1441003.3287.30.0072015-06-2023∶17∶543.02.262.702×10121.687±0.1151.742±0.14716.864±0.5033.363772.4221.20.0032015-07-0119∶31∶373.62.892.414×10131.469±0.3031.936±0.23312.840±3.7802.399887.3254.10.0152015-08-1415∶04∶213.62.731.407×10131.540±0.1291.805±0.12317.292±0.6683.477846.2242.30.0102015-09-1215∶51∶023.12.282.915×10121.578±0.1562.018±0.17519.699±1.1323.313826.3236.60.002

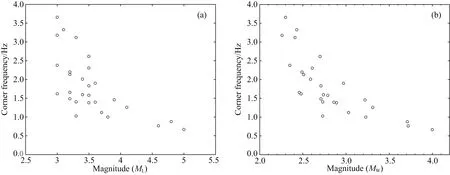
图4 反演得到的拐角频率与震级关系示意图Fig.4 Sketch of inverted corner frequency versus local magnitude (a) and moment magnitude (b)

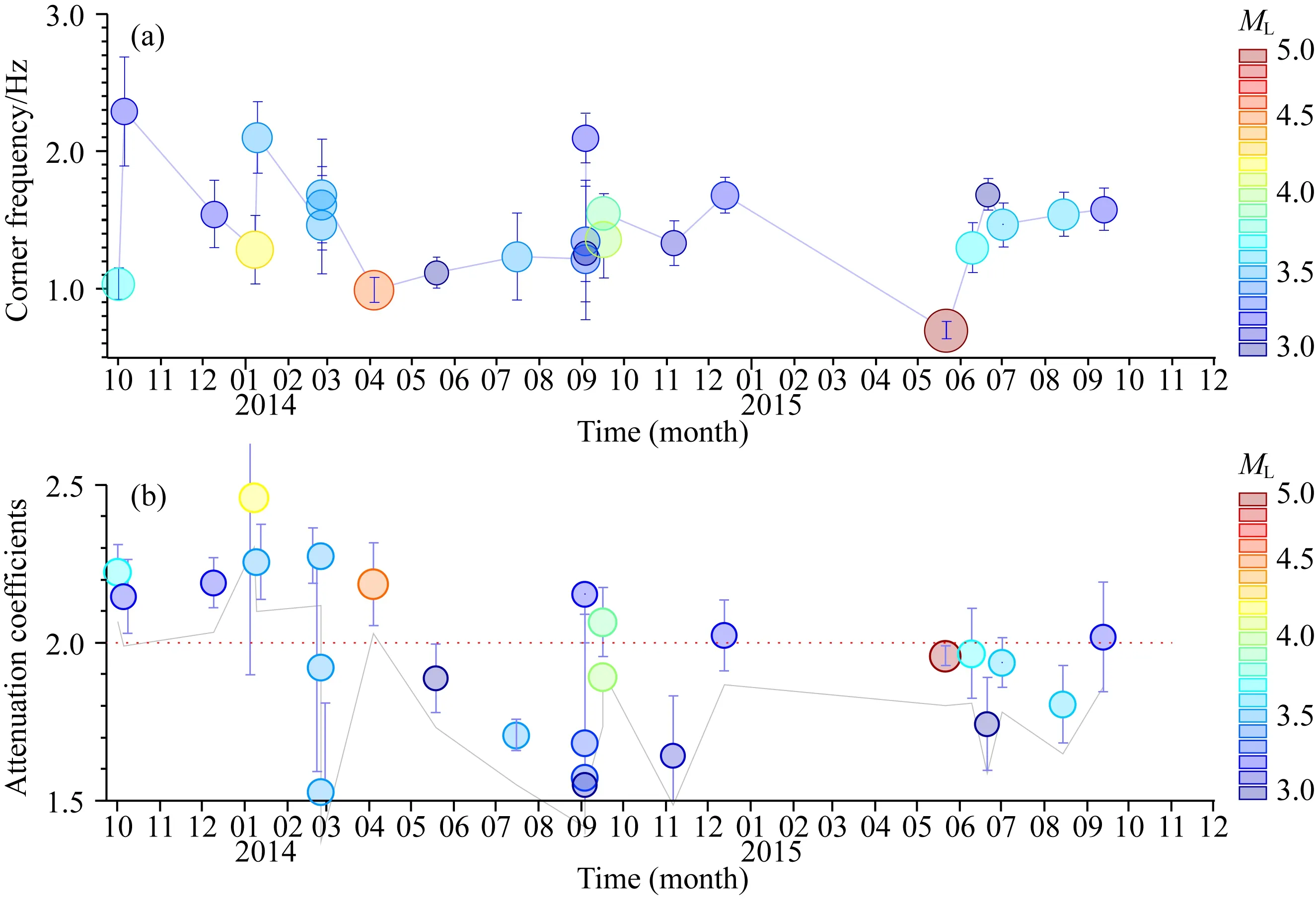
图5 乳山震群ML≥3.0事件的拐角频率(a)、衰减系数(b)随时间变化曲线Fig.5 Variations of corner frequency fC (a) and decay coefficients γ (b) with time

大体上说，受噪声干扰影响，震级越小，拐角频率的不确定性越大.与相同大小的余震事件相比，2013年10月1日ML3.8地震的拐角频率相对偏低，并且不确定性较小，这一现象或许和此次事件的性质(前震，其他相同大小事件均为余震)有关，也可能和震源区介质的破碎程度有关.

4.2 高频衰减系数

震源谱的高频衰减系数γ反映了地震破裂的运动学性质，反映了地震断层面的总体上的几何形态和地震破裂的传播过程，准确地测定这个常数在地震震源问题的研究中具有重要的实际意义(陈运泰等，2000).从反演结果来看，乳山震群的高频衰减系数大体在Brune理论设定的值γ=2附近.但伴随序列的发展，γ值存在显著变化：在序列前期γ>2，后期尤其是2014年4月4日ML4.4地震后γ值多小于2.这一现象，如前面所述，高频衰减系数γ的本质和断层面破裂的分形维有关，0<γ≤3，反映了断层破裂的复杂性，不同破裂模型的理论分析也证实了这一点*陈运泰，顾浩鼎．2007．震源理论基础(上册)．北京：中国科学院研究生院．1-191．.在经典的Brune模型下，断层面分形维D=2，γ=2；对于乳山震群前期的地震事件，γ>2，则D<2，说明这些事件的断层面模型相对简单；但到了震群活动的中后期，由于持续活动，震源区介质变得异常破碎，裂隙的扩展具有随机性，因此高频衰减系数γ<2，则断层面分形维D>2，说明这些事件的断层面上的破裂过程更加复杂.郑建常等(2015c)对2014年新疆于田7.3级地震序列的前震识别研究发现，与余震事件比较，可能由于障碍体的阻碍或者破裂不充分的原因，前震事件的高频成分更加丰富.由于γ在数学上等于频谱高频段拟合直线的斜率，因此γ值偏小，也就意味着频谱中高频成分的比例相对增加，与Chepkunas等(2001)对于前震得到的认识一致，这或许可以解释为乳山震群长时间持续活动的一个因素.

反演过程中我们注意到一个现象：2014年2月25日乳山震群发生多次ML3级余震，其中后两次事件γ值的不确定性明显偏大(±0.330和±0.281)，并且最后一次事件的高频衰减系数非常低(1.527).根据台网观测报告，后两次3级事件的发震时刻分别为：05∶23∶01.67和05∶23∶27.71，间隔仅26 s；因此波形记录变得复杂，以RCH台为例，由图6a可见后一次事件的记录中包含了前一次事件的尾波部分.可以认为，正是由于散射尾波的干扰，从而使高频衰减系数出现了异常的低值.

2014年2月25日乳山震群异常活跃，根据测震台网提供的观测报告，共记录到ML≥1.0级余震228次，其中ML≥0.0级126次，并且在05时23分之后的30 min内就记录到事件51次(图6).彭志刚等通过研究大震后的序列活动认为，较大地震发生后大量的微震事件被淹没了，因此他们通过较大事件的波形模版识别出了更多的微震(Peng et al.,2006,2007).可能正是因为这些震群剧烈活动时被淹没的微震事件，使得两次较大事件的高频衰减系数出现了小于2的低值和较大的不确定性.同样的现象也出现在2014年9月3日的4次ML3级余震的计算结果中(图5b)，这4次事件集中发生在从09时08分到10时30分的1.5 h内，这4次事件中有三次的高频衰减系数在1.6左右，不确定性大于0.25.

图6 2014年2月25日乳山震群M -t图(b)与RCH台05时23分两次事件波形(a)Fig.6 Raw observations of two horizontal components for the 2 events (a) at 05∶23 on Feb.25,2014 at the RCH station.Panel (b) gives the M -t plot of aftershocks occurred on this day

另外，由图5还可以看出，2月25日和9月3次两组低γ值出现的时段后，随即就是乳山震群两组显著的余震活动：2014年4月4日ML4.6和9月16日ML4.1、ML3.9地震.根据前面的分析，或许可以认为在震群发展过程中，随着震源区的不断破裂，由于较大障碍体的存在，破裂受到阻碍，使得发生破裂的断层面形态也趋于复杂，分形维升高，表现在震源谱上出现低γ值，随后较大障碍体发生破裂，发生几次显著的余震事件.

高频衰减系数与震源性质有密切的关系.吴忠良等(1999)把震源谱高频衰减常数及其随地震尺度的变化与应力降随地震尺度的变化联系起来.Patanè等(1994)对火山地区典型的流体侵入触发的微震事件的研究发现，这些事件的谱呈现ω-3的特征，也就是高频衰减系数γ≈3.我们利用乳山震群现场的密集台阵的到时资料研究发现，乳山震群可能存在流体触发的因素(郑建常等，2015b)；我们计算得到的乳山震群的γ值中有多次的95%置信下限大于2.0，最大值接近2.5.这些衰减系数偏高的事件，根据Patanè等(1994)的研究，则可能存在流体触发的因素.

4.3 截止频率fmax及其上的衰减系数p

从理论上说，截止频率fmax和地震发生的本质问题有关，即什么样的微破裂会最终导致地震？Fujiwara(1991)基于滑动弱化模型数值模拟研究了震源过程控制截止频率fmax的能力，假设非平面破裂存在凹凸体(asperities)的情况下，合成观测谱的高频端迅速下降，超过ω-2.Wen和Chen(2012)对汶川地震的计算结果中fmax在5～12 Hz，衰减系数p在2.0～4.0.在我们给出的模型中，p的值与他们的结果基本一致(2倍标准差范围约1.5～5.0，见表1).Fujiwara(1991)认为：如果设定地震由一组破裂和凹凸体组成，小的破裂和障碍体的相互作用确定了fmax，如果这些小的破裂和凹凸体的分布与震源大小独立，那么对所有地震，fmax将近乎常数.但从我们得到的结果来看，fmax好像与地震大小存在一定的相关关系(图7a1)，但随着震群的发展基本稳定(图7a2).

衰减系数p和震级的关系不明显(图7b1)，从随时间的变化来看，似乎与震群活动过程有关，但显然地，该参数受高频衰减系数γ的值及其不确定性的影响较大，因此图7b2显示出与图5b近乎反相关的变化.

4.4 破裂半径与应力降

虽然学术界对由震源谱导出的破裂半径的可靠性仍存在争议(Beresnev,2001,2002)，并且如前所述，不同的学者对导出破裂半径的关系式也给出了不同的系数，但鉴于研究的连贯性及便于和其他研究进行比较，我们在此处的讨论中仍然使用Brune给出的传统关系(公式(9))来估计破裂半径R.图8a给出了本文得到的破裂半径与矩震级的关系图，可以看出二者有很好的线性相关关系，与理论关系(陈运泰等，1976，图24)的形态也很一致.使用稳健回归拟合，得到二者的线性关系：MW=2.977+1.972×lgR.龙锋等(2006)通过1965年以来34次地震资料给出了华北地区面波震级和破裂长度的回归关系式：

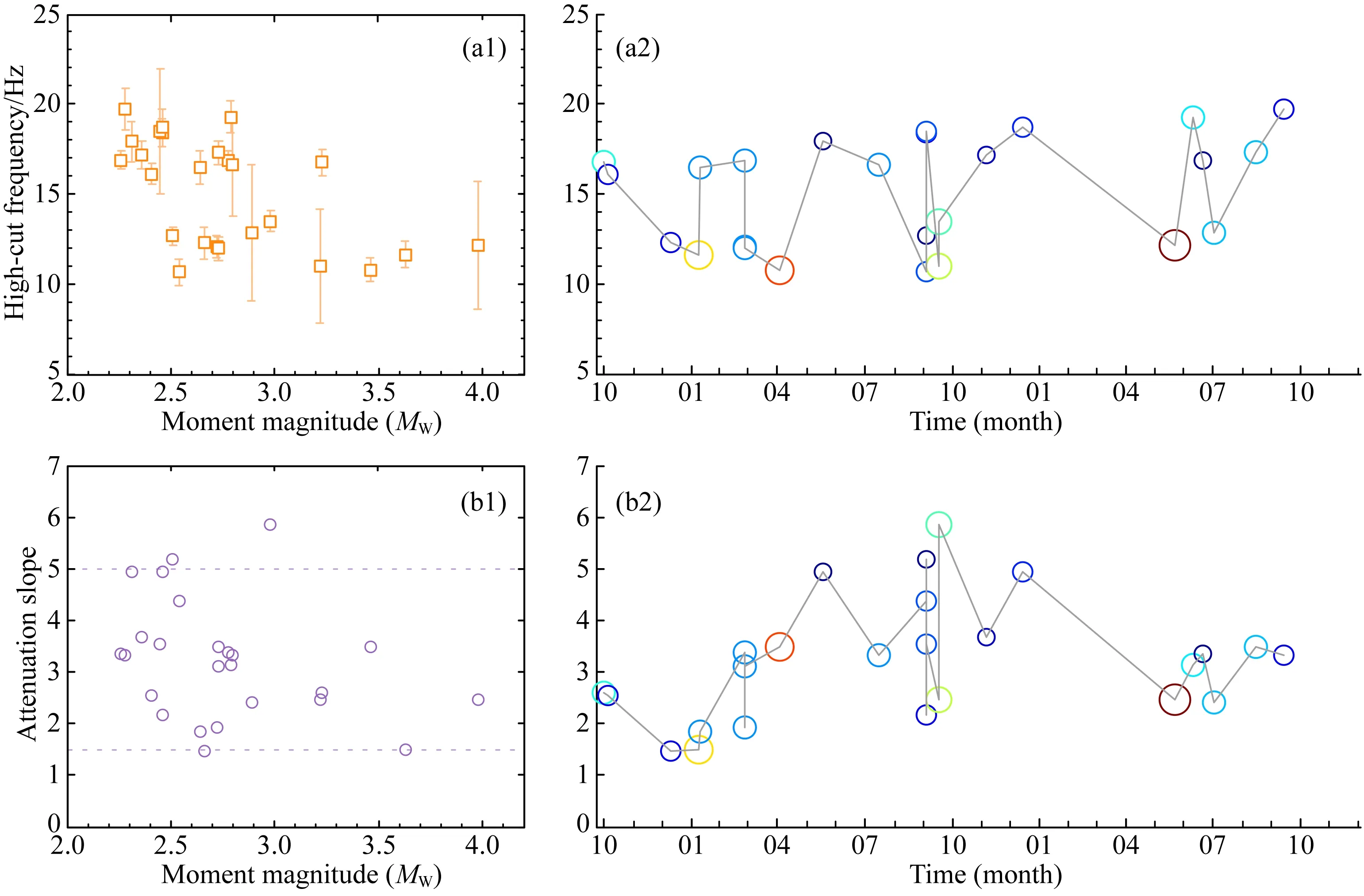
图7 反演得到的乳山震群ML≥3.0事件的截止频率fmax(上)以及衰减系数p(下)与震级关系图Fig.7 Inverted spectrum parameters of ML≥3.0 events of the Rushan swarm (a1) Variations of high-cut frequency fmax with moment magnitude;(a2) Variations of fmax with time;(b1) Variations of attenuation slope p beyond fmax with moment magnitude MW;(b2) Variations of p with time

图8 乳山震群ML≥3.0事件破裂半径(a)及应力降(b)与震级关系图Fig.8 Relationship between source parameters and moment magnitude derived from ML≥3.0 events of the Rushan swarm(a) Rupture radius R versus MW;(b) Stress drops σ versus MW.

MS=3.821+1.860×lgL.

(13)

按照该经验公式，对于一次MS3.0地震，其破裂长度L约362 m，设L=2R，则与我们根据公式(11)得到的反演结果有很好的一致性，说明由公式(11)给出的结果可能更接近实际的破裂尺度.以公式(11)得到的破裂半径结果进行拟合，得

MW=3.324+1.972×lgL,

(14)

与龙锋等(2006)的结果较为吻合.

一般情况下，由Brune模型以及经验关系导出的应力降与震级大小正相关(Harrington and Brodsky,2009).我们反演的结果也显示，应力降与震级之间有很好的线性关系(图8b).从数量级上看，我们反演的乳山震群25次ML≥3.0事件的应力降绝大多数不超过0.1 MPa，与其他学者得到类似大小地震的应力降值明显偏小(Harrington and Brodsky,2009)，郑建常等(2008)用Andrews谱积分法对相邻地区(同样位于胶东半岛，震中距约120 km，构造背景相近)的崂山震群应力降的计算结果显示，类似大小事件的应力降多在几个MPa；对于出现该差异的原因，一方面反映了不同区域构造应力水平的差异，另一方面，结合乳山震群活动持续时间长(2013年10月1日至今)、主震余震震级级差小的特点，可以认为这次震群活动属于低能量的破裂过程，这种低应力现象与乳山震群的弱衰减现象相一致.

de Lorenzo等(2004)研究意大利西西里岛东南地区的微震事件时也发现了类似的低应力降现象(259次事件，ML0.6～3.5，应力降在0.01～1 MPa，平均为0.1 MPa)，他们认为这些地震可能位于断层的弱化带(weakened zone)，无法积累较大的应力.从乳山震群的构造区域来看，胶东半岛位于胶辽断块，其周边的构造边界带如郯庐断裂带、蓬莱—威海断裂带及南黄海的千里岩断裂带等都是强震活跃区，历史上多次发生6、7级强(大)震，而胶东半岛的陆地区域有历史记载以来记录到的最大地震事件为51/2级，可能表明胶东半岛的构造特性和地质环境决定了该区无法积累大的应力.另外，对于乳山震群，我们研究未发现震中区有较大的断层展布(郑建常等，2015b)，通过精定位结果的分析认为可能是岩体边界的新生断裂活动，因此结合本文得到的低应力降结果，分析认为这可能意味着乳山震群是一个相对非耗散型(non-dissipative)的脆性破裂过程，属于Kanamori等(1998)提出的低摩擦应力的断层作用.

5 讨论与结论

本文引入频率上限fmax提出了基于Brune模型的高频截止(High-Cut)模型，采用两步反演的方法来拟合求解震源谱的特征参数，并给出其误差范围；实际应用显示该模型的理论谱对观测谱有很好的拟合，可明显改善传统方法得到的拐角频率识别的准确度.

将该方法应用于2013—2015年的乳山震群，并基于相对可靠的震源谱参数计算了乳山震群25次ML≥3.0事件的震源参数(地震矩、破裂半径、应力降等)，进一步对乳山震群的震源破裂特性进行了讨论.结果显示：

(1) 拐角频率、应力降与震源尺度大小明显相关.

(2) 拐角频率与截止频率之间高频衰减系数γ的大小，反映了震源偏离圆盘型破裂模型的程度，与震源区破裂复杂程度和破裂性质有关；混杂有微震破裂或其他事件波形的数据得到的γ<2，且不确定性变大.

(3) 截止频率fmax可能与组成地震的微破裂有关，反演结果显示该参数与地震大小存在一定相关性.

(4) 相比较Brune给出的公式，Beresnev(2001)给出的震源半径计算公式似乎更符合实际.乳山震群的研究结果显示，后者与华北地区的经验关系较为一致.

(5) 乳山震群的应力降明显偏小(最大不超过0.15 MPa)，一方面反映了震中区域较低的背景构造应力水平；另一方面，可能还意味着此次震群是一个相对非耗散型的脆性破裂过程，属于低摩擦应力的断层作用.

致谢 感谢两位匿名审稿人提出的建设性意见和建议！本文工作依托于山东省地震局“乳山台阵”项目，得到了山东省地震局刘敏、曲均浩、曲利、胡旭辉等以及乳山市科技局李英宇的大力协助，山东省地震预报研究中心赵金花、盖殿广、王庆林等在资料收集、报告整理方面也给予了很多帮助，在此深表感谢！

Allmann B P,Shearer P M.2009.Global variations of stress drop for moderate to large earthquakes.J.Geophys.Res.,114(B1):B01310,doi:10.1029/2008JB005821.

Andrews D J.1986.Objective determination of source parameters and similarity of earthquakes of different size.Geophysical Monographs,37(6):259-267.

Atkinson G M.1993.Earthquake source spectra in eastern North America.Bull.Seismol.Soc.Amer.,83(6):1778-1798.

Atkinson G M,Boore D M.1998.Evaluation of models for earthquake source spectra in eastern North America.Bull.Seismol.Soc.Amer.,88(4):917-934.

Baltay A,Ide S,Prieto G,et al.2011.Variability in earthquake stress drop and apparent stress.Geophys.Res.Lett.,38(6):L06303,doi:10.1029/2011GL046698.

Baltay A S,Hanks T C,Beroza G C.2013.Stable stress-drop measurements and their variability:Implications for ground-motion prediction.Bull.Seismol.Soc.Amer.,103(1):211-222,doi:10.1785/0120120161.

Bates D M,Watts D G.1988.Nonlinear Regression Analysis and Its Applications.New York:John Wiley &Sons,52-60.

Beresnev I A.2001.What we can and cannot learn about earthquake sources from the spectra of seismic waves.Bull.Seismol.Soc.Amer.,91(2):397-400.

Beresnev I A.2002.Source parameters observable from the corner frequency of earthquake spectra.Bull.Seismol.Soc.Amer.,92(5):2047-2048.

Beresnev I A.2009.The reality of the scaling law of earthquake-source spectra?.J.Seismol.,13(4):433-436,doi:10.1007/s1095-008-9136-9.

Boore D M.1983.Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra.Bull.Seismol.Soc.Amer.,73(6A):1865-1894.

Boore D M,Joyner W B,Fumal T E.1997.Equations for estimating horizontal response spectra and peak acceleration from western North American earthquakes:A summary of recent work.Seismol.Res.Lett.,68(1):128-153.

Boore D M.2003.Simulation of ground motion using the stochastic method.Pure Appl.Geophys.,160(3):635-676.

Boore D M,Di Alessandro C,Abrahamson N A.2014.A generalization of the double-corner-frequency source spectral model and its use in the SCEC BBP validation exercise.Bull.Seismol.Soc.Amer.,104(5):2387-2398.

Brune J N.1970.Tectonic stress and the spectra of seismic shear waves from earthquakes.J.Geophys.Res.,75(26):4997-5009.

Brune J N.1971.Correction [to “Tectonic stress and the spectra,of seismic shear waves from earthquakes”].J.Geophys.Res.,76(20):5002.

Chen Y T,Lin B H,Li X C,et al.1976.The determination of source parameters for small earthquakes in Qiaojia and Shimian and the estimation of potential earthquake danger.Chinese J.Geophys.(Acta Geophys.Sinica) (in Chinese),19(3):206-233.

Chepkunas L S,Rogozhin E A,Benikova V I.2001.Spectral characteristics of foreshocks preceding major earthquakes of the Kurile-Kamchatka Arc and their application to the prediction of the main shock time.Russian Journal of Earth Sciences,3(3):235-245.

Choy G L,Kirby S H.2004.Apparent stress,fault maturity and seismic hazard for normal-fault earthquakes at subduction zones.Geophys.J.Int.,159(3):991-1012.

de Lorenzo S,Di Grazia G,Giampiccolo E,et al.2004.Source and Qpparameters from pulse width inversion of microearthquake data in southeastern Sicily,Italy.J.Geophys.Res.,109(B7),doi:10.1029/2003JB002577.

Drouet S,Souriau A,Cotton F.2005.Attenuation,seismic moments,and site effects for weak-motion events:Application to the Pyrenees.Bull.Seismol.Soc.Amer.,95(5):1731-1748.

Frankel A.1995.Simulating strong motions of large earthquakes using recordings of small earthquakes:The Loma Prieta mainshock as a test case.Bull.Seismol.Soc.Amer.,85(4):1144-1160.

Fujiwara H.1991.High-frequency seismic wave radiation from antiplane cohesive zone model and fmaxas source effect.Bull.Seismol.Soc.Amer.,81(4):1115-1128.

Goebel T H W,Hauksson E,Shearer P M,et al.2015.Stress-drop heterogeneity within tectonically complex regions:A case study of San Gorgonio Pass,southern California.Geophys.J.Int.,202(1):514-528.

Hanks T C,Wyss M.1972.The use of body-wave spectra in the determination of seismic-source parameters.Bull.Seismol.Soc.Amer.,62(2):561-589.

Harrington R M,Brodsky E E.2009.Source duration scales with magnitude differently for earthquakes on the San Andreas fault and on secondary faults in Parkfield,California.Bull.Seismol.Soc.Amer.,99(4):2323-2334.

Hauksson E,Teng T L,Henyey T L.1987.Results from a 1500 m deep,three-level downhole seismometer array:Site response,low Q values,and fmax.Bull.Seismol.Soc.Amer.,77(6):1883-1904.

Hua W,Chen Z L,Zheng S H.2009.A study on segmentation characteristics of aftershock source parameters of Wenchuan M8.0 earthquake in 2008.Chinese J.Geophys.(in Chinese),52(2):365-371.

Ide S,Beroza G C.2001.Does apparent stress vary with earthquake size?.Geophys.Res.Lett.,28(17):3349-3352.

Iwakiri K,Hoshiba M.2012.High-frequency (>10 Hz) content of the initial fifty seconds of waveforms from the 2011 off the Pacific coast of Tohoku earthquake.Bull.Seismol.Soc.Amer.,102(5):2232-2238,doi:10.1785/0120110241.

Izutani Y.2008.Radiated energy from the Noto Hanto,Japan,earthquake of March 25,2007,and its aftershock.Earth,Planets and Space,60(2):145-150.

Izutani Y,Kanamori H.2001.Scale-dependence of seismic energy-to-moment ratio for strike-slip earthquakes in Japan.Geophys.Res.Lett.,28(20):4007-4010.

Jones L E,Helmberger D V.1998.Earthquake source parameters and fault kinematics in the eastern California shear zone.Bull.Seismol.Soc.Amer.,88(6):1337-1352.

Kanamori H,Anderson D L,Heaton T H.1998.Frictional melting during the rupture of the 1994 Bolivian earthquake.Science,279(5352):839-842.

Kane D L,Prieto G A,Vernon F L,et al.2011.Quantifying seismic source parameter uncertainties.Bull.Seismol.Soc.Amer.,101(2):535-543,doi:10.1785/0120100166.

Kaneko Y,Shearer P M.2014.Seismic source spectra and estimated stress drop derived from cohesive-zone models of circular subshear rupture.Geophys.J.Int.,197(2):1002-1015.

Kaneko Y,Shearer P M.2015.Variability of seismic source spectra,estimated stress drop,and radiated energy,derived from cohesive-zone models of symmetrical and asymmetrical circular and elliptical ruptures.J.Geophys.Res.,120(2):1053-1079.

Lancieri M,Madariaga R,Bonilla F.2012.Spectral scaling of the aftershocks of the Tocopilla 2007 earthquake in northern Chile.Geophys.J.Int.,189(1):469-480.

Lindley G T,Archuleta R J.1992.Earthquake source parameters and the frequency dependence of attenuation at Coalinga,Mammoth Lakes,and the Santa Cruz Mountains,California.J.Geophys.Res.,97(B10):14137-14154.

Liu J,Zheng S H,Wong Y L.2003.The inversion of non-elasticity coefficient,source parameters,site response using genetic algorithms.Acta Seismol.Sinica (in Chinese),25(2):211-218.

Long F,Wen X Z,Xu X W.2006.Empirical relationships between magnitude and rupture length,and rupture area,for seismogenic active faults in north China.Seismology and Geology (in Chinese),28(4):511-535.

Lyskova E L,Yanovskaya T B,Duda S J.1998.Spectral characteristics of earthquakes along plate boundaries.Geofizika,15(1):69-81.

Moya A,Aguirre J,Irikura K.2000.Inversion of source parameters and site effects from strong ground motion records using genetic algorithms.Bull.Seismol.Soc.Amer.,90(4):977-992.

Papageorgiou A S,Aki K.1983.A specific barrier model for the quantitative description of inhomogeneous faulting and the prediction of strong ground motion.I.Description of the model.Bull.Seismol.Soc.Amer.,73(3):693-722.

Papageorgiou A S.1988.On two characteristic frequencies of acceleration spectra:Patch corner frequency and fmax.Bull.Seismol.Soc.Amer.,78(2):509-529.

Patanè D,Ferrucci F,Gresta S.1994.Spectral features of microearthquakes in volcanic areas:Attenuation in the crust and amplitude response of the site at Mt.Etna,Italy.Bull.Seismol.Soc.Amer.,84(6):1842-1860.

Peng Z G,Vidale J E,Houston H.2006.Anomalous early aftershock decay rate of the 2004 Mw6.0 Parkfield,California,earthquake.Geophys.Res.Lett.,33(17),doi:10.1029/2006GL026744.

Peng Z G,Vidale J E,Ishii M,et al.2007.Seismicity rate immediately before and after main shock rupture from high-frequency waveforms in Japan.J.Geophys.Res.,112(B3),doi:10.1029/2006JB004386.

Qin J Z,Ye J Q,Qian X D,et al.2003.Source parameters of the Yao′an earthquakes in 2000.Chinese J.Geophys.(in Chinese),46(5):633-641,doi:10.3321/j.issn:0001-5733.2003.05.010.

Sereno Jr T J,Bratt S R,Bache T C.1988.Simultaneous inversion of regional wave spectra for attenuation and seismic moment in Scandinavia.J.Geophys.Res.,93(B3):2019-2035.

Shearer P M,Prieto G A,Hauksson E.2006.Comprehensive analysis of earthquake source spectra in southern California.J.Geophys.Res.,111(B6):B06303,doi:10.1029/2005JB003979.

Shi Y Y,Zheng S H,Hu X H,et al.2008.A study on seismic attenuation and site response in Shandong Area.South China Journal of Seismology (in Chinese),28(1):92-100.

Singh S K,Ordaz M.1994.Seismic energy release in Mexican subduction zone earthquakes.Bull.Seismol.Soc.Amer.,84(5):1533-1550.

Stankova-Pursley J,Bilek S L,Phillips W S,et al.2011.Along-strike variations of earthquake apparent stress at the Nicoya Peninsula,Costa Rica,subduction zone.Geochem.Geophys.Geosyst.,12(8):Q08002,doi:10.1029/2011GC003558.

Tusa G,Brancato A,Gresta S,et al.2006.Source parameters of microearthquakes at Mount St Helens (USA).Geophys.J.Int.,166(3):1193-1223.

Wang P,Zheng J C.2014.Temporal and spatial variation of apparent stress in Eastern Shandong Province.Earthquake (in Chinese),34(4):70-77.

Wen J,Chen X F.2012.Variations in fmaxalong the ruptured fault during the MW7.9 Wenchuan earthquake of 12 May 2008.Bull.Seismol.Soc.Amer.,102(3):991-998,doi:10.1785/0120110105.

Wu Z L,Chen Y T,Mozaffari P.1999.Scaling of stress drop and high-frequency fall-off of source spectra.Acta Seismol.Sinica (in Chinese),21(5):460-468.

Wu Z L.2001.Scaling of apparent stress from broadband radiated energy catalogue and seismic moment catalogue and its focal mechanism dependence.Earth,Planets and Space,53(10):943-948.

Yi G X,Wen X Z,Xin H,et al.2011.Distributions of seismicity parameters and seismic apparent stresses on the Longmenshan-Minshan tectonic zone before the 2008 Ms8.0 Wenchuan earthquake.Chinese J.Geophys.(in Chinese),54(6):1490-1500,doi:10.3969/j.issn.0001-5733.2011.06.008.

Zhang T Z,Ma Y S,Huang R L,et al.2000.The focus parameters and their correlation from small earthquakes before and after the 1995 Douhe earthquake.Acta Seismol.Sinica (in Chinese),22(3):233-240.

Zhao C P,Chen Z L,Hua W,et al.2011.Study on source parameters of small to moderate earthquakes in the main seismic active regions,China mainland.Chinese J.Geophys.(in Chinese),54(6):1478-1489,doi:10.3969/j.issn.0001-5733.2011.06.007.

Zheng J C,Pang Y S,Wan L C,et al.2008.Stress drop of the ML4.1 earthquake sequence in Laoshan,Qingdao.Seismological and Geomagnetic Observation and Research (in Chinese),29(4):17-23.

Zheng J C,Chen Y T.2012.Amplitude spectrum inversion for double-couple source model with particle swarm optimization algorithm.Acta Seismol.Sinica (in Chinese),34(3):308-322.

Zheng J C,Wang P,Lin M,et al.2013.Moment tensor inversion for 3 mid-strong earthquakes in U.S.using regional full waveforms.Progress in Geophys.(in Chinese),28(6):2825-2837,doi:10.6038/pg20130603.

Zheng J C,Lin M,Wang P,et al.2015a.Error analysis for focal mechanisms from CAP method inversion:An example of 2 moderate earthquakes in Jiaodong Peninsula.Chinese J.Geophys.(in Chinese),58(2):453-462,doi:10.6038/cjg20150209.

Zheng J C,Qu L,Qu J H,et al.2015b.Comparison of locations of Rushan earthquake swarm from Large and small network.Seismology and Geology (in Chinese),37(4):953-965.

Zheng J C,Wang P,Xu C T,et al.2015c.Spectral characteristics of 2014 Yutian MS7.3 earthquake sequence and its application in foreshock discrimination.Earthquake Research in China (in Chinese),31(2):253-261.

Zhou S Y,Xu Z H.2000.Fracture characteristics of the 1997 Jiashi,Xinjiang,China,earthquake swarm inferred from source spectrum.Acta Seismol.Sinica (in Chinese),22(2):113-124.

Zollo A,Orefice A,Convertito V.2014.Source parameter scaling and radiation efficiency of microearthquakes along the Irpinia fault zone in southern Apennines,Italy.J.Geophys.Res.,119(4):3256-3275.

附中文参考文献

陈运泰,林邦慧,李兴才等.1976.巧家、石棉的小震震源参数的测定及其地震危险性的估计.地球物理学报,19(3):206-233.

陈运泰,吴忠良,王培德等.2000.数字地震学.北京:地震出版社,1-171.

华卫,陈章立,郑斯华.2009.2008年汶川8.0级地震序列震源参数分段特征的研究.地球物理学报,52(2):365-371.

刘杰,郑斯华,黄玉龙.2003.利用遗传算法反演非弹性衰减系数、震源参数和场地响应.地震学报,25(2):211-218.

龙锋,闻学泽,徐锡伟.2006.华北地区地震活断层的震级-破裂长度、破裂面积的经验关系.地震地质,28(4):511-535.

秦嘉政,叶建庆,钱晓东等.2003.2000年姚安地震的震源参数.地球物理学报,46(5):633-641,doi:10.3321/j.issn:0001-5733.2003.05.010.

石玉燕,郑斯华,胡旭辉等.2008.山东地区地震动衰减和场地响应的研究.华南地震,28(1):92-100.

王鹏,郑建常.2014.鲁东地区视应力时空变化特征分析.地震,34(4):70-77.

吴忠良,陈运泰,Mozaffari P.1999.应力降的标度性质与震源谱高频衰减常数.地震学报,21(5):460-468.

吴忠良.2003.地震辐射能量和震源谱.∥中国地震局监测预报司.地震参数——数字地震学在地震预测中的应用.北京:地震出版社,1-163.

易桂喜,闻学泽,辛华等.2011.2008年汶川MS8.0地震前龙门山—岷山构造带的地震活动性参数与地震视应力分布.地球物理学报,54(6):1490-1500,doi:10.3969/j.issn.0001-5733.2011.06.008.

张天中,马云生,黄蓉良等.2000.1995年陡河地震前后小震震源参数及其相互关系.地震学报,22(3):233-240.

赵翠萍,陈章立,华卫等.2011.中国大陆主要地震活动区中小地震震源参数研究.地球物理学报,54(6):1478-1489,doi:10.3969/j.issn.0001-5733.2011.06.007.

郑建常,潘元生,万连初等.2008.青岛崂山ML4.1地震序列应力降变化研究.地震地磁观测与研究,29(4):17-23.

郑建常,陈运泰.2012.基于粒子群优化的双力偶模型振幅谱反演方法及应用.地震学报,34(3):308-322.

郑建常,王鹏,林眉等.2013.区域全波形反演美国三次中强地震的震源矩张量.地球物理学进展,28(6):2825-2837,doi:10.6038/pg20130603.

郑建常,林眉,王鹏等.2015a.CAP方法反演震源机制的误差分析:以胶东半岛两次显著中等地震为例.地球物理学报,58(2):453-462,doi:10.6038/cjg20150209.

郑建常,曲利,曲均浩等.2015b.乳山震群大小台网地震定位的对比研究.地震地质,37(4):953-965.

郑建常,王鹏,许崇涛等.2015c.2014年于田MS7.3地震序列的频谱特征分析及其前震识别.中国地震,31(2):253-261.

周仕勇,许忠淮.2000.由震源谱推断1997年新疆伽师强震群破裂特性.地震学报,22(2):113-124.

(本文编辑 何燕)

Robust inversion of seismic-source spectral parameters for the 2013—2015 Rushan swarm

ZHENG Jian-Chang1,WANG Peng1,XU Chang-Peng1,XU Chong-Tao2,LIU Kai3,LI Dong-Mei1,LI Cui-Qin1

1 Earthquake Administration of Shandong Province,Jinan 250014,China2 Wulian Seismic Station,Shandong Wulian 262300,China3 Dezhou Seismic Station,Shandong Dezhou 253000,China

Based on the Brune′s model,we propose a high-cut model by introducing the cut-off frequency-fmax.We use a two-step inversion method to fit the observed seismic-source spectra and resolve its characteristic parameters,i.e.corner frequency,low-frequency level,attenuation coefficient.Additionally,95% confidence level is given by a particle swarm nonlinear optimization algorithm.Tests on real data show that this method can improve the accuracy of spectra parameters significantly.This method is applied to the 2013—2015 Rushan swarm which has continued for over two years,including more than 10000 aftershocks recorded.Source parameters,such as scalar moment,rupture radius,and stress drop for 25 ML≥3.0 events of this swarm are calculated using the method aforementioned.The results show that (1) the corner frequency and stress drop are evidently correlated with the source scale or event size.(2) The attenuation coefficientγ,which implies the deviation to the Brune′s circular model,is related with the complexity and features of the rupture area.Examples show that if records are contaminated by other events or mixed with micro cracks,the high-frequency attenuation coefficientγis greater than 2 with larger uncertainty.(3) The cut-off frequency fmaxmight be connected with micro cracks of an event,and also has correlation with the event size.(4) The source radius derived from Beresnev′s formula (2001) is more suitable in North China,which is in agreement with previous study.(5) The Rushan swarm has obviously lower stress drops,implying this swarm is a relatively non-dissipative brittle rupture process,or a faulting with low frictional stress.

Source parameters;Corner frequency;Rupture radius;Stress drop;High frequency attenuation coefficients

郑建常，王鹏，徐长朋等.2016.乳山震群震源谱参数的稳健反演.地球物理学报，59(11):4100-4112,

10.6038/cjg20161114.

Zheng J C,Wang P,Xu C P,et al.2016.Robust inversion of seismic-source spectral parameters for the 2013—2015 Rushan swarm.Chinese J.Geophys.(in Chinese),59(11):4100-4112,doi:10.6038/cjg20161114.

中国地震局星火计划项目(XH15026)、山东省科技发展计划项目(2014GSF120007)与山东省地震局重点项目(SD1250501)联合资助.

郑建常，1978年生，山东临清人，副研，2011年于中国地震局地球物理研究所获博士学位，主要从事地震活动性及数字地震学研究.E-mail：zjcmail@yeah.net

10.6038/cjg20161114

P315

2015-09-27，2016-07-12收修定稿