基于神经网络的蓄电池荷电状态估算

戴武昌，王建国，徐天锡

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.国网淄博供电公司，山东 淄博 255000)



基于神经网络的蓄电池荷电状态估算

戴武昌1，王建国1，徐天锡2

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.国网淄博供电公司，山东 淄博 255000)

针对蓄电池荷电状态(SOC)的估算问题，将神经网络算法应用于此以估算蓄电池荷电状态。通过神经网络输入参数的选择建立了蓄电池SOC估算模型，并基于BP神经网络和RBF神经网络对蓄电池分别进行SOC的估算。结果表明：神经网络应用于蓄电池SOC估算所得的结果准确度高。通过比较可以得出，BP神经网络相对于RBF神经网络预测结果更准确，且具有相对较好的抗干扰能力，能够更加准确的估算出蓄电池SOC。

荷电状态；神经网络；估算；BP神经网络

蓄电池作为最常见的储能环节被应用在生产生活的各个方面：在清洁能源的开发利用中，电池储能技术可以用来平抑波动功率；在电动汽车中可以作为主电源为汽车提供动力支持；在变电站直流系统中作为备用电源保证变电站中的二次设备可靠运行等[1-2]。在实际应用中，时刻掌握蓄电池的剩余容量十分必要，蓄电池的剩余容量用SOC来表示。SOC即电池荷电状态，美国先进电池联合会(USABC)在《电动汽车电池实验手册》中做如下定义：在一定的放电倍率条件下，电池的剩余电量与相同条件下额定容量的比值，即：

SOC=Qc/CI，

(1)

式中:Qc为剩余电量；CI为电池以恒定电流I放电时具有的容量[3-4]。

目前SOC并不能被直接测量，只能通过电压、电流、温度、内阻等参数估算获得。常用的SOC估算方法有以下几种：①线性模型法：基于经验方程和等效电路或者数学模型的估计方法。这些方法对测量误差和错误的初始条件具有很好的鲁棒性，但是这种稳态模型却不能完全正确的适应电池的动态特性。②安时计量法：在提供SOC初值的情况下，通过计算放电的总电量得到当前SOC。在保证初值及测量精度的情况下，一定时间间隔内是一种简单且可靠的方法，否则误差将会累加。③开路电压法：蓄电池开路电压能够较为准确的反映蓄电池的SOC，并且简单易行，但是蓄电池需要长时间空载静置后才可获取，因此难以应用在实际中。④内阻法：此方法放电后期具有较高精度和较好适应性，但电池单体内阻检测困难，且放电初期内阻变化不大，因此测量难度大。⑤卡尔曼滤波法：对模型的精度要求非常高，计算量大且算法较为复杂。⑥阻抗谱方法：充、放电的电流强度以及蓄电池循环充、放电历史对其结果有一定的影响需要修正，且不适合实际应用[5-10]。

将神经网络方法应用于蓄电池SOC估算时，依靠神经网络的四个特性能够有效的解决上述问题的存在：①自学习和自适应性：当输入参数发生变化时，相当于给神经网络输入新的学习样本，网络能够自动调整结构参数，改变映射关系，从而对特定的输入产生相应的期望输出。②非线性性：神经网络将知识存储于连接权值中，可以实现各种非线性映射。③鲁棒性与容错性：神经网络具有信息存储的分布性，故局部的损害会使神经网络的精度适度减小，但不会对误差累加也不会产生灾难性的错误。④计算的并行性与存储的分布性：由于其并行结果决定了每个神经元都可以根据接受到的信息进行独立运算和处理，并输出结果，大大提升运算速度[11]。本文首先介绍了BP神经网络和RBF神经网络的特性并确定了神经网络的结构，而后依据选择的输入参数建立了估算模型，通过磷酸铁锂电池实验平台采集数据，最后通过仿真实验加以验证，并对结果进行分析。

1 神经网络

1.1 BP神经网络

BP神经网络，即误差反向传播算法的学习过程，由信息的正向传播和误差的反向传播两个过程组成。包括输入层、隐含层和输出层。输入层各神经元负责接收来自外界的输入信息，并传递给中间层各神经元；中间层是内部信息处理层，负责信息变换，根据信息变化能力的需求，中间层可以设计为单隐含层或者多隐含层结构；最后一个隐含层传递到输出层各神经元的信息，经进一步处理后，完成一次学习的正向传播处理过程，由输出层向外界输出信息处理结果。当实际输出与期望输出不符时，进入误差的反向传播阶段。误差通过输出层，按误差梯度下降的方式修正各层权值，向隐含层、输入层逐层反传。周而复始的信息正向传播和误差反向传播过程，是各层权值不断调整的过程，也是神经网络学习的过程，此过程一直进行到网络输出的误差减少到可以接受的程度，或者预先设定的学习次数为止。本文选择如图1所示的典型三层结构的BP神经网络。

图1 三层BP网络

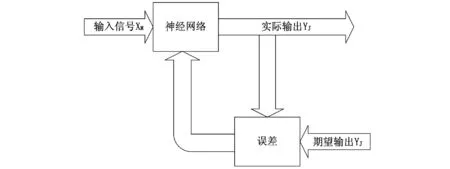
图2 网络学习原理

神经网络初始权值选择净输入为零点附近的极小值，并且保证初始权值数量正负各半。在神经网络中为了发挥网络适应性及搜索能力，隐含层传递函数选用Tan-Sigmod函数，使网络对任意输入量映射在-1到1之间，由于蓄电池SOC范围在0到1 之间，所以输出层采用Log-Sigmod函数将最终输出映射在0到1之间，可以加快收敛速度，提高收敛精度。

图2描述BP神经网络学习基本原理，通过对多个样本进行反复的学习并通过误差的反向传播来修改连接权值，它是沿着输出误差函数的负梯度方向对其进行改变，并且到最后使误差函数收敛于该函数的最小点。为了在修正权值时避免计算Hessian矩阵，减小计算量，加快收敛速度，优化误差反向传播算法鲁棒性差，易陷入局部最优等问题。本文采用L-M(Levenberg-Marquardt)算法优化网络学习过程，L-M算法根据下式修正网络权值：

ω(n+1)=ω(n)-ηn{H(n)+βnQ(n)}-g(n)，

(2)

式中：ω(n+1)为修正后的权值，ω(n)为当前权值，ηn为学习率，H(n)为传递函数在ω(n)处的二阶梯度矩阵，即Hessian矩阵，Q(n)为给定的正定矩阵，g(n)为传递函数在ω(n)处的梯度向量，当βn=0时，L-M算法变为牛顿法；当βn很大时，此算法相当于步长较小的梯度下降法，而雅克比矩阵比Hessian矩阵易于计算，因此收敛速度快。

1.2 RBF神经网络

RBF神经网络是有三层构成的前向网络：第一层为输入层，节点个数等于输入的维数；第二层为隐含层，节点个数视具体问题而定；第三层为输出层，节点个数等于输出数据的维数。RBF神经网络不同层有着不同的功能，隐含层是非线性的，采用径向基函数作为基函数，从而将输入向量空间转换到隐含层空间，使原来线性不可分的问题变得线性可分，输出层是线性的。RBF网络的基本思想是：用RBF作为隐含层单元的“基”构成隐含层空间，可以将输入矢量不通过权值连接而直接映射到隐含层空间。当RBF的中心点确定以后，映射关系则随之确定。而隐含层空间到输出空间是线性映射，即网络的输出是隐含层单元输出的线性加权和。可以通过修正此处的权值来学习网络。由此可见，从整体来看，网络由输入到输出的映射是非线性的，而网络输出对可调参数而言却又是线性的。这样网络的权值就可以通过求解线性方程获得，从而大大加快学习速度并避免局部极小问题。图3所示为RBF网络结构。

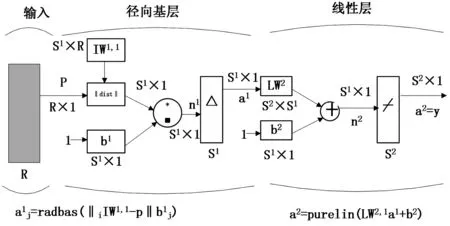
图3 径向基函数网络结构

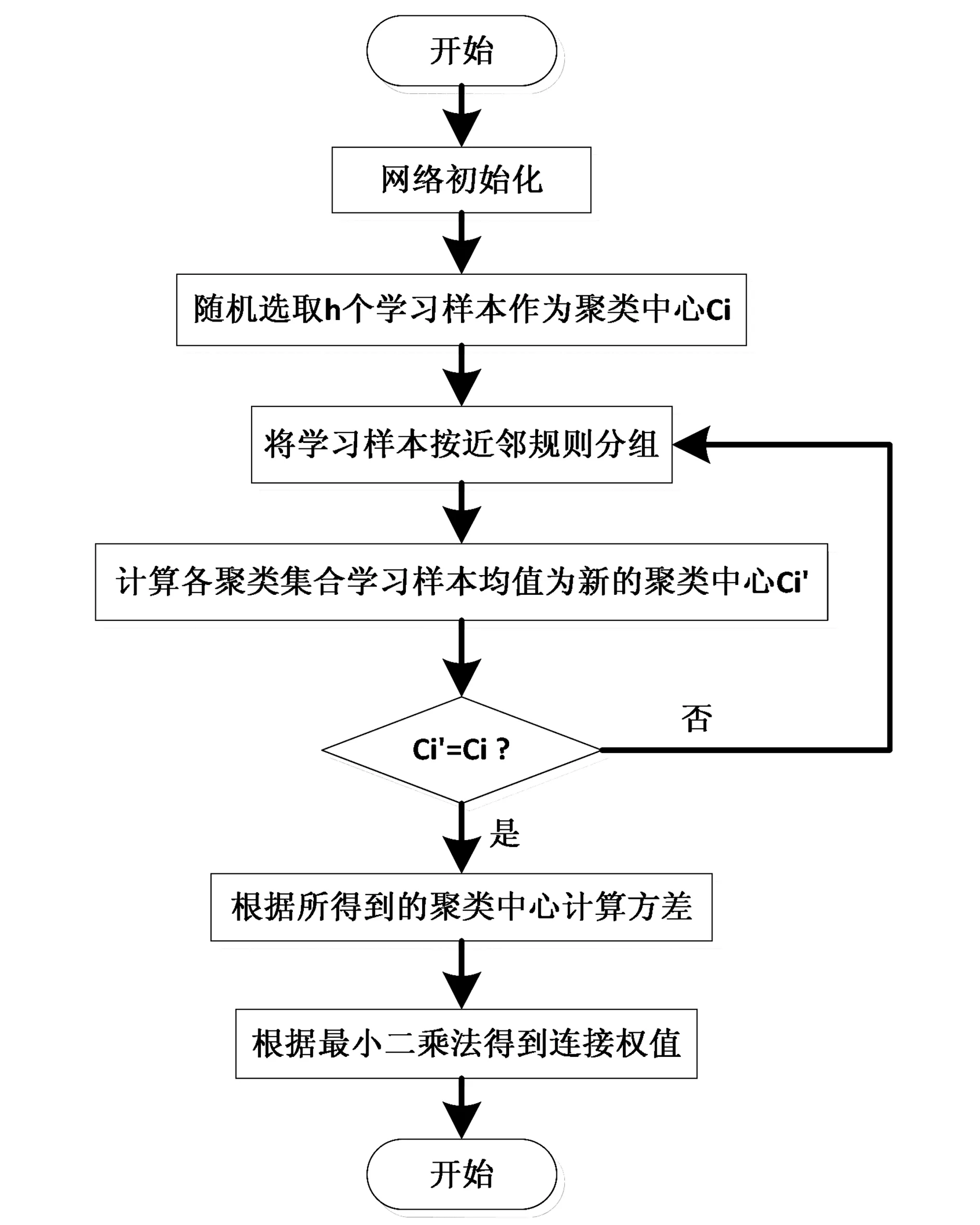
图4 RBF网络学习算法具体步骤

网络的输出为

a2=purelin(LW2a1+b2)，

(3)

a1=radbas(n1)，

(4)

(5)

式中：diag(x)表示取矩阵向量主对角线上元素组成的列向量；“∧”和“*”分别表示数量乘方和数量乘积(即矩阵中各对应元素的乘方和乘积)。

RBF神经网络的学习算法需要求解的参数有三个：基函数的中心、方差以及隐含层到输出层的权值。根据径向基函数中心选取方法的不同，RBF网络有不同的学习算法，常见的有随机选取中心法、自组织选取中心法、有监督选取中心法和正交最小二乘法等。本文将采用自组织选取中心的RBF神经网络学习算法。此学习算法由两个阶段组成：一是自组织学习阶段，此阶段为无监督学习过程，其任务是用自组织聚类方法为基函数确定合适的聚类中心，并根据聚类中心的距离确定其方差；二是有监督学习阶段，此阶段任务是用有监督学习算法修正隐含层到输出层之间的权值，通过权值的不断修正减小误差并提高收敛速度，提高网络预测精度。有监督学习算法具体步骤如图4所示。

2 SOC估算模型

蓄电池SOC是多种因素共同作用的结果，通常包括温度、充放电倍率、蓄电池SOH(健康状态)、电压、内阻等。而在生产生活中蓄电池的工作环境、工作条件各不相同。因此，准确计算SOC的难点在于SOC与各因素之间复杂映射关系的存在。传统的蓄电池SOC估算精度较差的原因在于其方法只针对一种因素寻找其映射关系，并未考虑其他因素对蓄电池SOC估算的影响，所以考虑并不全面。而神经网络在蓄电池SOC估算中可以针对多个输入量寻找其映射关系，故可以相对提高估算精度。本文选择蓄电池的工作电压、工作电流以及工作温度三个参数作为神经网络的输入并以蓄电池SOC作为输出，通过网络训练从而达到预期效果。构建如下式所示的蓄电池SOC估算模型：

SOC=f(V，I，T).

(6)

若要实现复杂的映射关系，则需要有足够的隐含层节点，在实际应用中往往根据经验和反复试验得到。下式为确定隐含层节点的常用公式：

I=2M+Q，

(7)

式中：I为隐含层节点数;M、Q分别为输入层、输出层节点数。依据式(7)初步确定隐含层节点数为7，并以网络的训练误差和训练次数为依据通过多次训练对其进行修正。如表1所示，当隐含层节点为7个和8个时训练次数相对较少，但是由于隐含层为8个节点时，误差最小，因此确定隐含层节点数为8个。

表1 不同隐含层节点数目训练效果

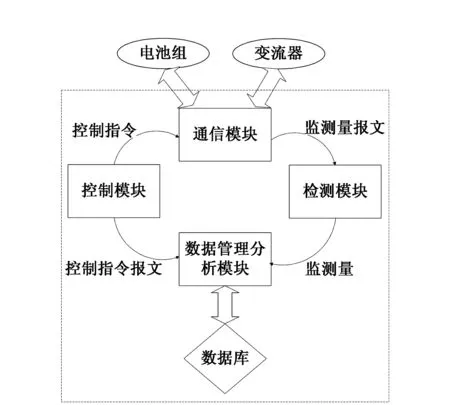
图5 ESMU结构

3 实验分析

3.1 数据采集以及处理

本文通过磷酸铁锂电池实验平台获得神经网络的样本数据，实验平台由磷酸铁锂电池、变流器以及锂电池能量管理系统组成。电池组由192节40 Ah磷酸铁锂电池串联而成，分为16箱，每箱12节；10 kW/20 kWh锂电池能量管理系统由储能管理单元(Energy Storage Manage Unit，ESMU)和电池管理单元(Battery Manage Unit，BMU)两部分组成，其中ESMU由通信模块、控制模块、监测模块和数据管理分析模块构成，可实现对电池的充放电控制、状态监测与数据管理分析。其具体结构如图5虚线框内所示：

将磷酸铁锂电池充满电后充分静置，进行一次放电实验，实时监测并记录电压、电流、温度以及SOC数据。采集得到300组数据，由于所得到的数据基本度量单位并不统一，同时为了加快网络训练的收敛速度，需要将数据进行归化处理，采用下式对电压、电流、温度数据进行归化处理，将输入样本数据归化到[0-1]之间。

(8)

3.2 仿真分析

将所得数据的2/3作为网络的训练样本，另外1/3用于检测训练效果。依据所建立的SOC估算模型，将用于测试网络训练效果的数据分别载入BP神经网络和RBF神经网络，所得到的SOC预测数据和两种模型下的误差见图6、图7所示：

图6 神经网络SOC预测结果图7 神经网络SOC预测误差

由图6、图7可以看出，当将同一组检测样本载入两种神经网络时，BP神经网络预测效果明显好于RBF神经网络预测效果，从均方误差来看，RBF网络预测误差相对较大，并且有很大的波动，而BP网络预测误差变化相对平缓，相对于RBF网络具有较好的抗干扰能力。

4 结 论

本文针对于蓄电池SOC估算问题，将BP神经网络和RBF神经网络应用于此。应用磷酸铁锂电池实验平台采集数据，将锂电池电压、电流、温度作为输入，将蓄电池SOC作为输出对网络进行训练，并用实测数据对网络进行检验预测锂电池SOC。仿真表明，神经网络应用于蓄电池SOC的估算具有很好的效果，可以满足蓄电池SOC估算要求，并且BP神经网络的预测效果明显优于RBF网络的预测效果。与此同时，神经网络训练速度快，适应性强，故可广泛应用于蓄电池SOC的在线估算，具有很好的实用价值与应用前景。

[1] 李军徽，冯喜超，朱星旭，等.10KW/20KWh锂电池能量管理系统的设计与实现[J].太阳能学报，2014，35(12):2490-2496.

[2] 吕帅帅，汪兴兴，倪红军，等.电动汽车能量管理系统的功能及研究进展[J].电源技术，2014，38(2):386-389.

[3] US Department of energy.USABC Electric Vehicle Battery Test Procedure Manaual[M].Washington:US Departmento f Energy，1996：33-135.

[4] 乔立彪.锂离子电池管理系统的研究与实现[D].济南:山东大学，2012.

[5] 乔波强，候振义，王佑民.蓄电池剩余容量预测技术现状及发展[J].电源世界，2012(2):21-26.

[6] 林成涛，陈全世，王军平，等.用改进的安时计量法估计电动汽车动力电池SOC[J].清华大学学报：自然科学版，2006，46(2):247-251.

[7] John Chiassion.Estimating the State of charge of a battery[J].IEEE Transactions on Control Systems Technology，2005，13(3):465-470.

[8] Taesic Kim，Wei Qiao.Online state of charge and electrical impedance estimation for Multicell lithium-ion batteries(C).IEEE Transportation Electrification Conference and Expo(ITEC)，2013:1-6.

[9] Novie Ayub Windarko，Jaeho Choi.Li-pb battery SOC estimation using extended kalman filter improved with variation of single dominant[J].Parameter Journal of Power Electronics，2012，12(1):40-48.

[10] 张金龙.动力电池组SOC估算及均衡控制方法研究[D].天津:天津大学，2011:5-23.

[11] 邢晓敏，刘洪涛，等.基于BP 神经网络的高精度基波频率检测方法研究[J].东北电力大学学报，2015，35(1):42-45.

[12] 朱政.磷酸铁锂电池荷电状态估计方法的研究[D].哈尔滨:哈尔滨工业大学，2013:1-116.

Estimation of Battery State of Charge Based on Neural Network

DAI Wu-chang1，WANG Jian-guo1，XU Tan-xi2

(1.School of Electric Engineering，Northeast Dianli University，Jilin Jilin 132012；2.State Grid Zibo Electric Power Company,Zibo Shan Dong 255000)

For the estimation of the state of charge(SOC) of the battery，The neural network algorithm is applied to estimate the residual capacity of the battery.In this paper，the selection of neural network input parameters to establish a battery SOC estimation model，and based on the BP neural network and RBF neural network to estimate the SOC.The results show that the neural network is more accurate in estimating the SOC of the battery.By comparison，it can be known that the BP neural network is more accurate than the RBF neural network，and it has a relatively good anti-interference ability，can more accurately estimate the battery SOC.

State of charge；Neural network；Estimation；BP neural network

2016-04-12

戴武昌(1963-)，男，吉林省吉林市人，东北电力大学电气工程学院研究员，主要研究方向：电机控制、储能技术.

1005-2992(2016)05-0001-06

TM912

A