多跨预应力混凝土桥梁结构动力特性研究

秦 力，张友奇，宫森保紀，Soumya Ranjan Harichandan

(1.东北电力大学 建筑工程学院，吉林 吉林 132012；2.北見工业大学 社会環境工学院，日本 北海道 0908507；3.印度科技大学 土木工程学院，印度 瓦朗加尔 506004)



多跨预应力混凝土桥梁结构动力特性研究

秦 力1，张友奇1，宫森保紀2，Soumya Ranjan Harichandan3

(1.东北电力大学 建筑工程学院，吉林 吉林 132012；2.北見工业大学 社会環境工学院，日本 北海道 0908507；3.印度科技大学 土木工程学院，印度 瓦朗加尔 506004)

基于振动理论的桥梁损伤检测方法需要精确提取桥梁的动力参数，动力参数识别是桥梁损伤检测的首要步骤。为了提取5跨预应力混凝土简支梁桥的动力参数，在桥梁上进行了两组振动试验，分别研究了每跨桥梁的动力特征和5跨桥梁的整体振动特性。所有单跨的4阶动力参数将根据智能无线传感器测量结果，应用快速傅立叶变换、半功率带宽法和交叉反应谱法计算得到。同时也讨论了振动传输，激励跨桥梁和非激励跨桥梁之间的关系。研究结果表明：桥墩长度会影响桥梁的自振频率；存在碎石均布荷载的情况下振动可以在所有跨桥梁之间传播；受竖向激励的一跨桥梁主振型为弯曲模态，非激励跨桥梁主振型趋向于扭转模态。研究结果将作为桥梁健康监测技术的基础研究。

多跨；预应力混凝土；桥梁；振动实验；动力参数；桥梁健康监测

随着桥梁技术的不断发展，桥梁结构的老朽化也越来越引起学者们的关注。发展桥梁结构健康监测技术，已经显得尤为重要。

如今，大多数桥梁结构健康监测研究主要集中在构件水平，如板式结构[1-3]，钢筋混凝土梁[4-5]等。构件的损伤检测实验可以有效地根据动力参数或换算参数的改变定位损伤。但由构件实验得出的结论是否可以应用到复杂的实际工程仍具有很大的不确定性。故仍然需要更多实际工程桥梁实验[6-8]来探究桥梁损伤定位的方法。

结构健康监测的主要目的之一是找到可以检测结构不可见损害的方法。然而，桥梁不可见损伤检测和定位是一个非常具有挑战的课题。目前，基于振动方式的损伤检测方法已经得到了广泛认可[9]，但由于结构的特异性，许多结论尚不能广泛应用，尚需要更多实际工程实验研究来完善损伤定位理论。实际工程桥梁结构的动力参数识别是损伤定位技术的首要步骤，动力参数识别的准确性直接关系到能否成功定位桥梁结构的损伤。

1 实验桥梁简介

无加川桥位于日本北海道北见市北部，如图1-3所示桥梁种类为5跨预应力混凝土简支梁桥，跨度为32.02 m，全长158.8 m。使用功能为铁路桥。桥梁建于1977年，现已停止使用，且桥上的铁轨和枕木已经拆除。跨与跨之间不连续，存在9cm的缝隙。在跨间伸缩缝处有金属盖板覆盖，整桥均布碎石荷载，如图4所示。

图1 无加川桥总览图

图2 无加川桥设计图

图3 桥基和桥墩高度详图

图4 碎石荷载

2 桥梁振动实验

2.1 实验简介

基于振动的桥梁结构损伤检测方法需要精确提取桥梁的动力参数，如自振频率、阻尼和主振型。桥梁结构动力参数提取的准确性直接关系到能否成功检测到桥梁结构的损伤。本次实验的目的为深入理解多跨预应力混凝土简支梁桥的动力特性，作为探索桥梁损伤定位方法的基础研究。

无加川桥梁结构动力特征的提取主要基于两组振动实验，每组实验中包括5次实验，总计10次实验。

第一组实验(实验1-实验5)主要目的为提取每一跨的自振频率、阻尼和主振型。传感器分布方式如图5-6所示，10个Imote2无限智能节点搭载SHM-H加速度传感器被安装在某一跨桥面的两侧，如图5所示。激励方式为两个成年人在跨中处起跳并大力着陆。

第二组实验(实验6-实验10)主要为了研究在某一跨上受到冲击荷载时，其他跨桥梁的振动情况。由于碎石均匀连续覆盖在桥面上，如果碎石的刚度和碎石与主梁之间的相互作用都被考虑，独立的5跨在一定程度上被连接成了一个整体结构。碎石使整个桥梁的结构形式和动力参数变的更加复杂。在第二组实验中，传感器分布方式如图5-6所示，10个Imote2无线智能节点搭载SHM-H加速度传感器被安装在整个桥梁结构上，每跨的中点的左右两侧各安放一个传感器。在第1跨、第2跨交界处和第4跨、第5跨交界处增设两个Imote2智能无线节点，用以保证长距离无线信号传输的稳定性。第二组实验激励方式同为两个成年人依次在各跨中处起跳并大力着陆。

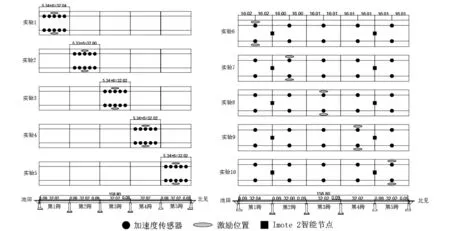
图5 传感器分布图

图6 传感器安装位置

2.2 数据处理方法

智能无线加速度传感器采样频率为280Hz，测量时间为60s，激励两次。每次实验可以得到十通道垂直方向的加速度数据。所有数据应用快速傅里叶变换得到振动的频域信息，自振频率由峰值拾取法获得，阻尼由半功率带宽法计算得到，主振型由交叉能量谱方法计算得到。

3 实验结果

3.1 第一组实验结果

定义无加川桥从池田方向到北见方向依次为第1跨到第5跨，由实际测量得到的各跨桥梁的自振频率和阻尼已列在表1中，实测得到各跨桥梁的主振型见表2。拾取到的4阶模态可以总结为：第一模态和第四模态为弯曲模态，第二模态和第三模态为扭转模态。由表1可知，第2跨和第3跨的第一模态和第二模态自振频率明显小于第1跨、第4跨和第5跨的第一模态和第二模态自振频率。5跨桥梁的设计相同，经过人工核查后，可以排除由施工误差引起的5跨之间的构造或尺寸差异导致较大的自振频率差异。所有跨桥梁都采用线支座，故由支座形式差异导致的自振频率差异也被排除。桥墩和桥基的不同高度将是导致这一现象的首要原因。由图3可知，桥墩4高度明显低于其它桥墩，当桥梁结构振动时，线支座的位移很小，可视其为固定支座。所以如果一跨主梁与其两侧的桥墩或桥基被视为一个框架结构，如图7所示，这个现象就很容易解释了。假设跨度是定值，桥墩越长，桥梁-桥墩整体框架结构的自振频率越低；桥墩越短，桥梁-桥墩整体框架结构的自振频率越高。经有限元模型验证，以上结论成立。

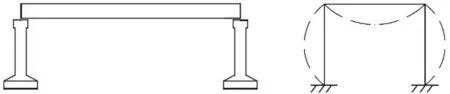
图7 主梁-桥墩刚架模型

跨模态1模态2模态3模态4自振频率阻尼自振频率阻尼自振频率阻尼自振频率阻尼14.20460.00737.6230.011221.33070.007627.65470.022223.93110.01247.17860.008821.29650.006428.37260.016833.99950.00956.83680.010121.33070.009928.06490.012644.34140.00628.40920.006721.98020.005729.94510.005554.17040.00718.40920.007321.98020.005130.18430.0093

表2 各跨主振型

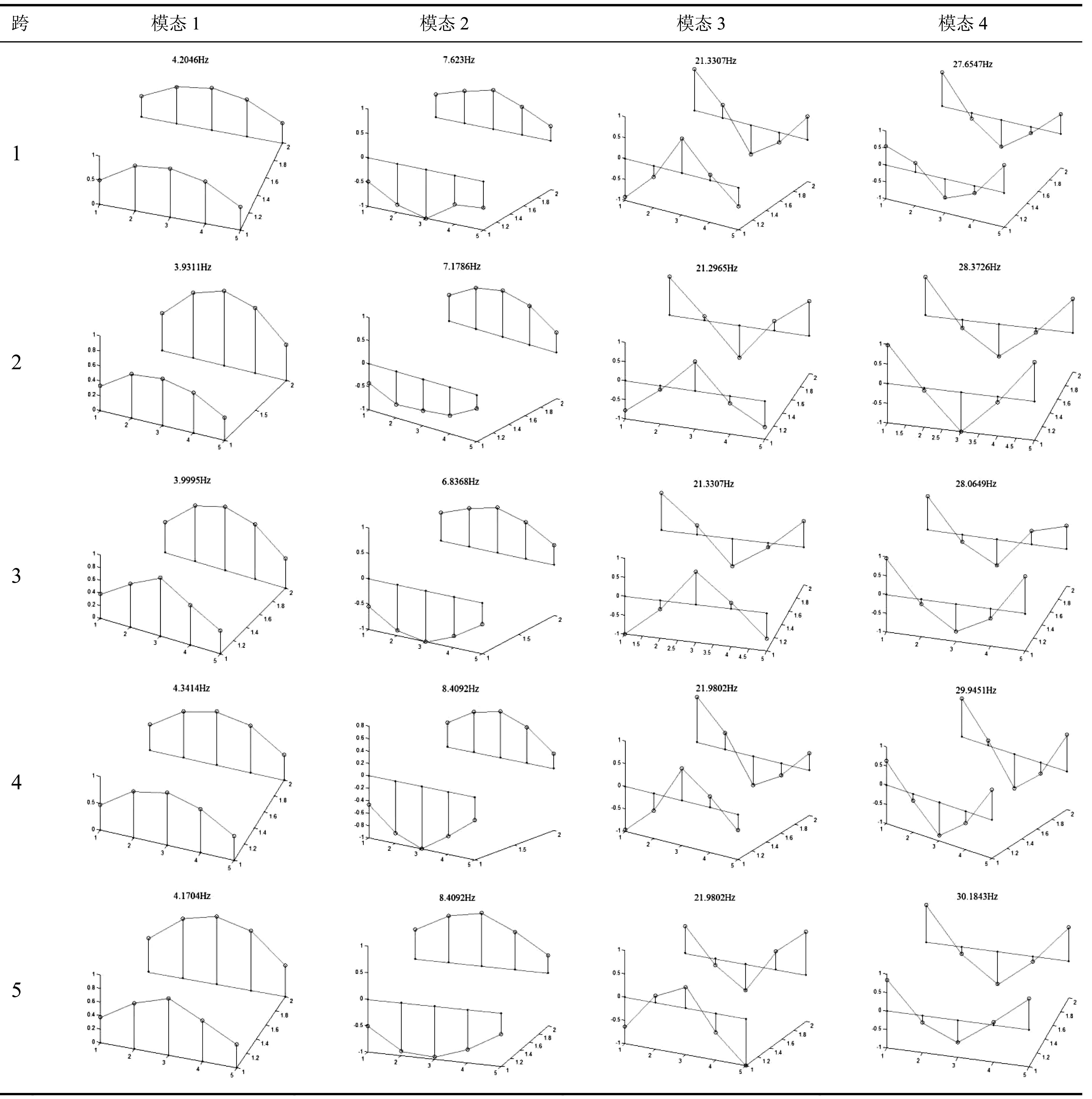
所有跨桥梁的第三模态和第四模态的自振频率也基本符合以上分析结论，第2跨和第3跨的第三模态和第四模态自振频率由于较高的桥墩导致自振频率低于第4跨和第5跨。第5跨桥梁因为与桥墩4和桥基相连，所以其第三模态和第四模态的自振频率都是最高的。第1跨的第三模态自振频率仅低于第2跨且和第3跨相同，第1跨的第4模态自振频率达到最低值，这与之前得出的结论有冲突。这一反常现象可能为以后的结构探伤研究提供线索，故在以后的研究中，第1跨桥梁应该优先进行探伤实验研究。

3.2 第二组实验结果

由第一组实验结果可得，所有跨的第一模态自振频率都在4 Hz左右，且第2跨的第一模态自振频率值最低。为了清楚的显示激励跨与非激励跨第一模态频率之间的关系，选取激励位置位于第2跨的实验7的功率谱作为研究对象，频率轴被指定为从3 Hz至5 Hz，如图8所示。因为每跨桥梁上安装了两个无线智能加速度传感器，所以每跨桥梁上将得到两个通道的数据。从图8中可以看出，在所有跨上的两个通道的功率谱中，都可以在3.931 1 Hz(第2跨第一模态自振频率)处清晰的拾取到峰值。这说明激励跨桥梁动力参数会对非激励跨桥梁造成影响，激励跨桥梁的自振将作为振源，其它跨桥梁在一定程度上将做受迫振动。在所有非激励跨桥梁的功率谱中，除了接收到激励跨桥梁的第一模态频率峰值外，每跨桥梁自身的第一模态振动频率也可以被清晰的拾取到，但其自身的第一模态频率峰值能量级数会随着与激励跨桥梁的距离增大而逐渐占优。例如在与第2跨桥梁相邻的第1跨和第3跨桥梁的功率谱中，第2跨桥梁的第一模态自振频率峰值将传播到第1跨和第3跨中，且第1跨和第3跨自身的第一模态自振频率4.204 6 Hz和3.999 5 Hz也可以清晰的拾取，但其自身的自振频率已不在占优，振动能量级数基本持平于传播来的第2跨第一模态自振频率，甚至被第2跨第一模态自振频率的能量级数峰值超过。而在距离激励跨更远的第4跨和第5跨桥梁中，其自身第一模态振动频率能量级数已明显超过第2跨桥梁的第一模态振动频率能量级数。总览图8，可以看出第二跨的第一模态自振频率峰值可以传播到其它非振动跨，在图8中已用竖线标出；其他非振动跨桥梁自身的第一模态振动频率峰值也将被保留。

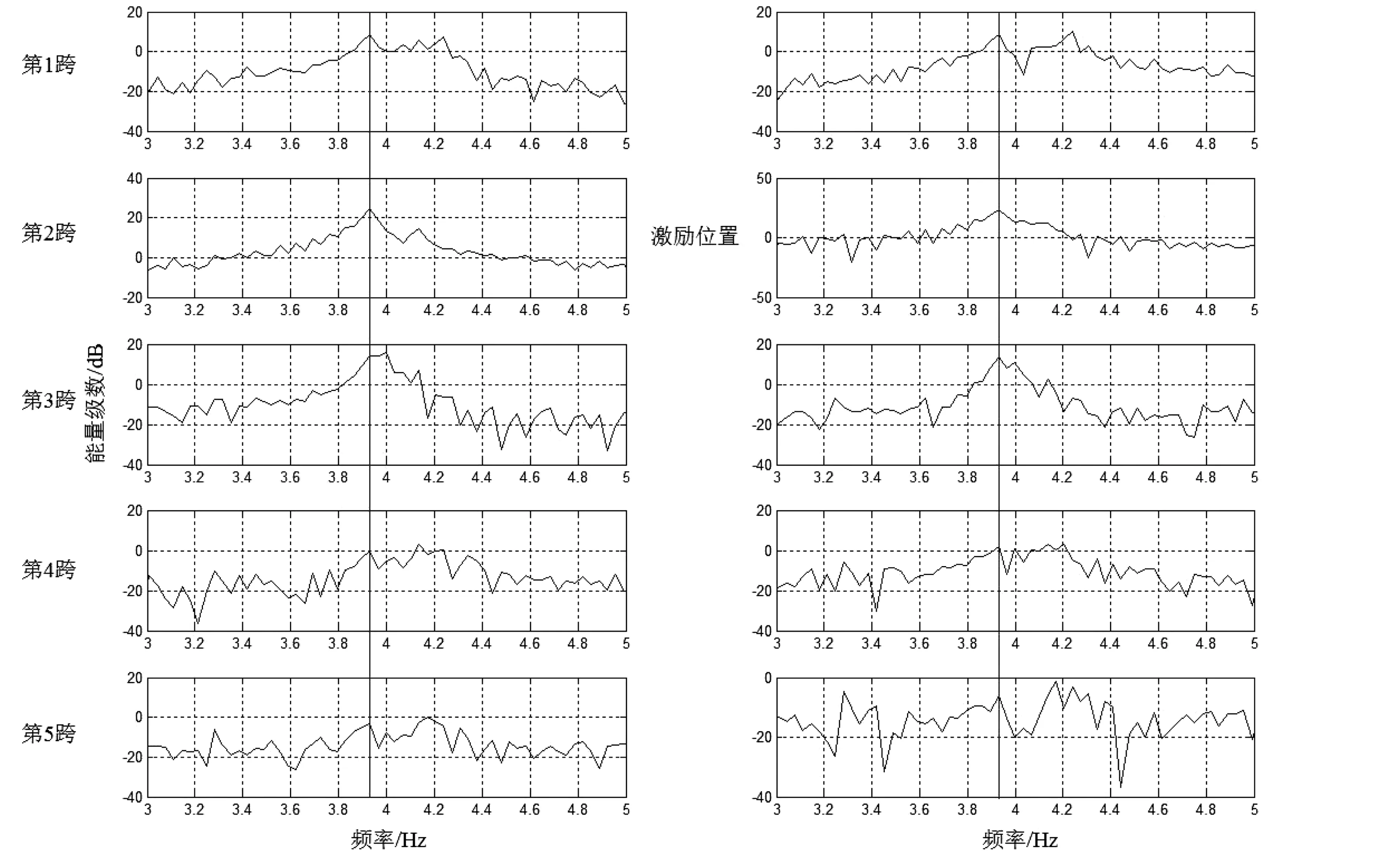
图8 实验7能量谱

在桥梁结构跨中位置垂直方向激励的冲击荷载所引起的振动，一般情况下主要振动模态都是一阶对称弯曲模态，其次是一阶反对称扭转模态。在激励跨中，能量谱上可以清晰的反映出第一模态(一阶对称弯曲模态)峰值能量级数大于第二模态(一阶对称弯曲模态)峰值能量级数。而在非激励跨中，主要振型随着与激励跨距离的远近而变化。如激励跨相邻的跨中，第一模态和第二模态都可能成为主要模态，频率峰值能量级数差别不大，而在距离激励跨更远端的非激励跨，第二模态成为主要模态。图9为实验6十通道能量谱的总览，频率轴范围指定为3 Hz-10 Hz，图9符合以上规律，即在第1跨中第一模态为主要模态；第2跨中第一模态和第二模态的能量级别基本相同，无法清晰的识别主要模态；第3跨至第5跨中第二模态为主要模态。

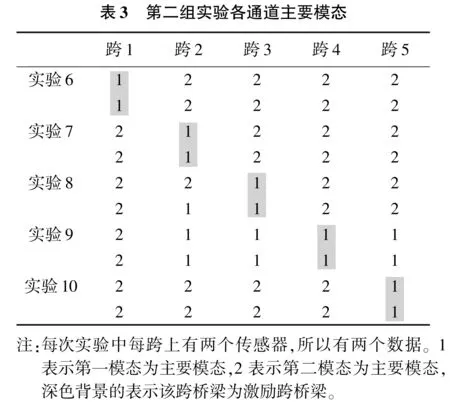
在第二组实验的5次实验中，每次实验每跨的主要模态情况已被归纳在表3中。从表3和图9可以得出：在激励跨桥梁中，第一模态频率峰值的能量级数明显高于非激励跨，且第一模态为该跨的主要模态。在与激励跨桥梁相邻跨桥梁中，主要模态可以为第一模态和第二模态，但第二模态是主要模态的概率稍大。在距离激励跨桥梁更远的跨中，第二模态成为主要模态。总览表3可以得到如下结论：从激励跨桥梁到远端非激励跨桥梁，主要模态情况将呈现从第一模态向第二模态逐步转变的趋势。呈现这一现象的原因非常复杂，这需要掌握桥墩振动的详细情况，了解振动如何从桥面传递到桥墩中，并从桥墩传递到下一跨桥面，还需要更多实验研究。

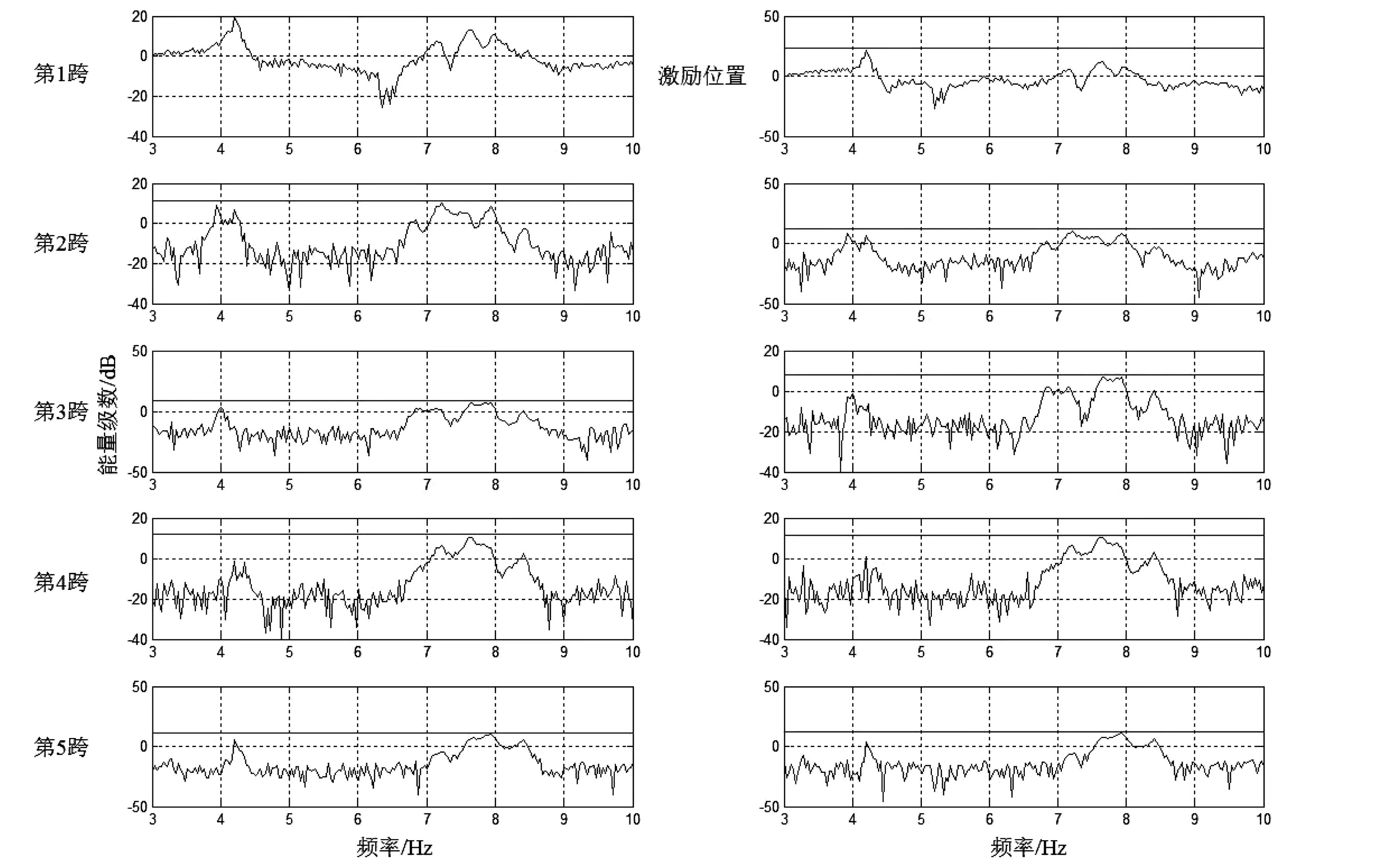
图9 实验6能量谱

4 结 论

以下结论基于5跨预应力混凝土简支梁桥的振动实验。

第一部分着力于精确提取每一跨桥梁的动力参数，包括自振周期、阻尼和主振型。从实验结果中可以得出以下结论：(1)在一个多跨预应力混凝土简支梁桥的实际工程中，自振频率计算需要将主梁、桥墩和桥基同时考虑成门式框架结构，以达到精确计算的目的。相同设计的主梁，不同高度的桥墩或桥基也会得到不同的实测自振频率。(2)第1跨高阶模态自振频率的异常可能对桥梁损伤探测给出提示，还需要更加深入的研究。

第二部分着重研究了跨与跨之间的动力反应和相互作用。可以得到以下两点结论：(1)激励跨桥梁和非激励跨桥梁的动力行为关系可以归纳为：激励跨桥梁的第一模态频率峰值可以传播到其他非激励跨桥梁，同时其他非激励跨桥梁也将保持其自身的第一模态频率峰值。(2)从激励跨桥梁向远端非激励跨桥梁，主要模态呈现从第一模态向第二模态逐渐过渡的趋势。

多跨预应力混凝土简支梁桥的动力参数研究将作为桥梁健康监测技术的基础研究。动力参数的识别和分析也是开展桥梁损伤定位的首要步骤。在将来的研究中，还需要对此多跨预应力混凝土简支梁桥的动力参数进行更加深入的研究，为损伤识别技术能在实际工程中广泛应用打下良好基础。

[1] Wei F.，Qiao P.A 2-D continuous wavelet transform of mode shape data for damage detection of plate structures[J].International Journal of Solids & Structures，2009，46(46):4379-4395.

[2] Lopes H.M.R.，Santos J.V.A.D.，Soares C.M.M.，et al.A numerical-experimental method for damage location based on rotation fields spatial differentiation[J].Computers & Structures，2011，89(19/20):1754-1770.

[3] Sbarufatti C.，Manson G.，Worden K.A numerically-enhanced machine learning approach to damage diagnosis using a Lamb wave sensing network[J].Journal of Sound & Vibration，2014，333(19):4499-4525.

[4] Tondreau G.，Deraemaeker A.Automated data-based damage localization under ambient vibration using local modal filters and dynamic strain measurements:Experimental applications[J].Journal of Sound & Vibration，2014，333(26):7364-7385.

[5] Kim J.T.，Park J.H.，Hong D.S.，et al.Hybrid health monitoring of prestressed concrete girder bridges by sequential vibration-impedance approaches[J].Engineering Structures，2010，32(1):115-128.

[6] Siringoringo D.M.，Fujino Y.，Nagayama T.Dynamic Characteristics of an Overpass Bridge in a Full-Scale Destructive Test[J].Journal of Engineering Mechanics，2013，139(6):691-701.

[7] Türker T.，Bayraktar A.，Bayraktar A.Structural safety assessment of bowstring type RC arch bridges using ambient vibration testing and finite element model calibration[J].Measurement，2014，58(8):33-45.

[8] Dilena M.，Morassi A.Dynamic testing of a damaged bridge[J].Mechanical Systems & Signal Processing，2011，25(5):1485-1507.

[9] Boller C.，Chang F.，Fujino Y.Encyclopedia of Structural Health Monitoring[M].A John Wiley And Sons，Ltd，2009.

Study on Dynamic Characteristics of a Muti-Span PC Bridge

QIN Li1，ZHANG You-qi1，MIYAMORI Yasunori2，SOUMYA Ranjan Harichandan3

(1.Archstecture Engineering College，Northeast Dianli University，Jilin Jilin 132012；2.Society and Environment Engineering，Kitami Institute of Technology College，Hokkaido Japan，0908507；3.Civil Engineering College，National Institute of Technology，Warangal India 506044)

Bridge damage detection method based on vibration theory needs to accurately extract the dynamic parameters of the bridge，and dynamic parameter identification is the first step of bridge damage detection.In order to extract the dynamic parameters of 5-span pre-stressed concrete simply supported beam bridge，two groups of vibration tests were carried out.The dynamic characteristics of every single span and the overall vibration characteristics of the all spans were studied.4 dynamic modal parameters of every single span were calculated with peak picking method，half power method and cross spectrum method based on the smart wireless sensor measurement results.At the same time，the vibration transmission，the relation between the excitation span and the no excitation spans were also discussed.Results show that:the length of the pier had effect to the natural frequencies；vibration can spread across all spans with ballast uniformly distributed load；the predominant mode of the span with vertical excitation was bending mode，and the predominant mode of no excitation spans more likely behave the torsional mode.The research results will be used as the foundation study of the bridge health monitoring technology.

Multi-span；Pre-stressed concrete；Bridge；vibration experiment；Dynamic parameters；Health monitoring

2016-03-10.

日本学術振興会JSPS Grant-in-Aid for Scientific Research(C) Grant Number 15K06176

秦 力(1972-)，男，辽宁省葫芦岛市人，东北电力大学建筑工程学院教授，博士，主要研究方向:高性能混凝土与结构理论研究，输电线路工程研究.

1005-2992(2016)05-0073-07

TP29

A