电缆载流量试验热稳定判据及试验误差的研究

鲁志伟，张 航，敖 明，于 海，李艳飞

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.吉林省电力有限公司 电力科学研究院，长春 130021；3.国网淄博供电公司，淄博 255000；4.广东电网公司广州供电局，广州 510620)



电缆载流量试验热稳定判据及试验误差的研究

鲁志伟1，张 航1，敖 明2，于 海3，李艳飞4

(1.东北电力大学 电气工程学院，吉林 吉林 132012；2.吉林省电力有限公司 电力科学研究院，长春 130021；3.国网淄博供电公司，淄博 255000；4.广东电网公司广州供电局，广州 510620)

运行中电力电缆线芯温度随负荷电流和电缆本体及周围媒质热特性参数的变化而变化，准确地确定电缆暂态温度场和线芯温度是提高电缆输送能力的基础。针对有限差分法计算电缆温度场难以处理电缆圆形边界和周围土壤矩形边界的问题，采用阶梯直线代替电缆圆形边界，在直角坐标系中直接求解电缆暂态温度场。基于坐标组合的有限差分法和大电流模拟试验验证该方法的有效性和实用性。计算程序分析了恒定负荷电流下电缆线芯的温升过程和载流量试验误差。计算结果表明：电缆线芯温升速度随土壤热阻系数的增加和电缆根数的增加而减慢，目前载流量试验中采用的热稳定判据可以使载流量试验值显著高于载流量实际值。

电力电缆；暂态温度场；有限差分法；载流量试验；热稳定判据；试验误差

在人口稠密的大城市，电力通常通过电力电缆传输[1]。为确保电缆安全运行和降低电缆使用成本，对电力电缆输送能力进行数值计算和试验研究具有重要意义[2，3]。载流量试验研究时对电缆施加恒定电流，电缆线芯温度逐渐上升并趋于稳定，并规定当线芯温度在4 h内变化≤1.0 ℃时，电缆线芯温度达到稳定状态[4，5]。电缆线芯温升速度取决于系统热时间常数，其值为电缆的状态监测及故障预警提供理论依据[6]。研究热稳定判据及可能带来的载流量试验误差，需对电缆暂态温度场进行数值计算。国际电工委员会推荐的载流量计算方法(IEC-60287)使用方便，适用于均匀土壤[7-9]，对于有回填土的不均匀土壤，使用修正系数进行修正，但其计算精度与回填土热阻系数和电缆回路数密切相关[10]。与IEC计算方法比较，数值计算方法精度高，适用于各种复杂工况，但编程繁琐且计算速度慢。电缆温度场数值计算通常采用边界元法[11]、有限元法[12-15]和有限差分法[16-21]。边界元法处理多回路电缆敷设问题时，边界过多使得计算量变大。有限元法可以灵活布置网格和节点，对复杂区域和复杂边界问题具有很好的适应性，在电缆温度场的计算中得到了广泛的应用。使用有限差分法计算电缆温度场时，一般同时采用极坐标系和直角坐标系，该方法被称为坐标组合法。极坐标易于处理电缆圆形边界，而直角坐标易于处理土壤区域外边界。坐标组合法在迭代过程中通过插值将两种坐标相结合，因此编程复杂，计算速度低。本文使用直线阶梯拟合曲线的方法对电缆圆形边界进行网格划分，将电缆影响区域全部划分到直角网格内，编程简单并且有较高的精度，便于大规模电缆集群敷设后的暂态温度场的数值采集及计算。

1 电缆暂态温度场计算模型

1.1 电缆暂态温度场的数学模型

由于电缆轴线方向温度几乎不变化，故可以采用二维计算模型，并采用有限差分法离散计算区域[22，23]。在图1直角坐标网格系统中，二维温度场暂态导热方程为：

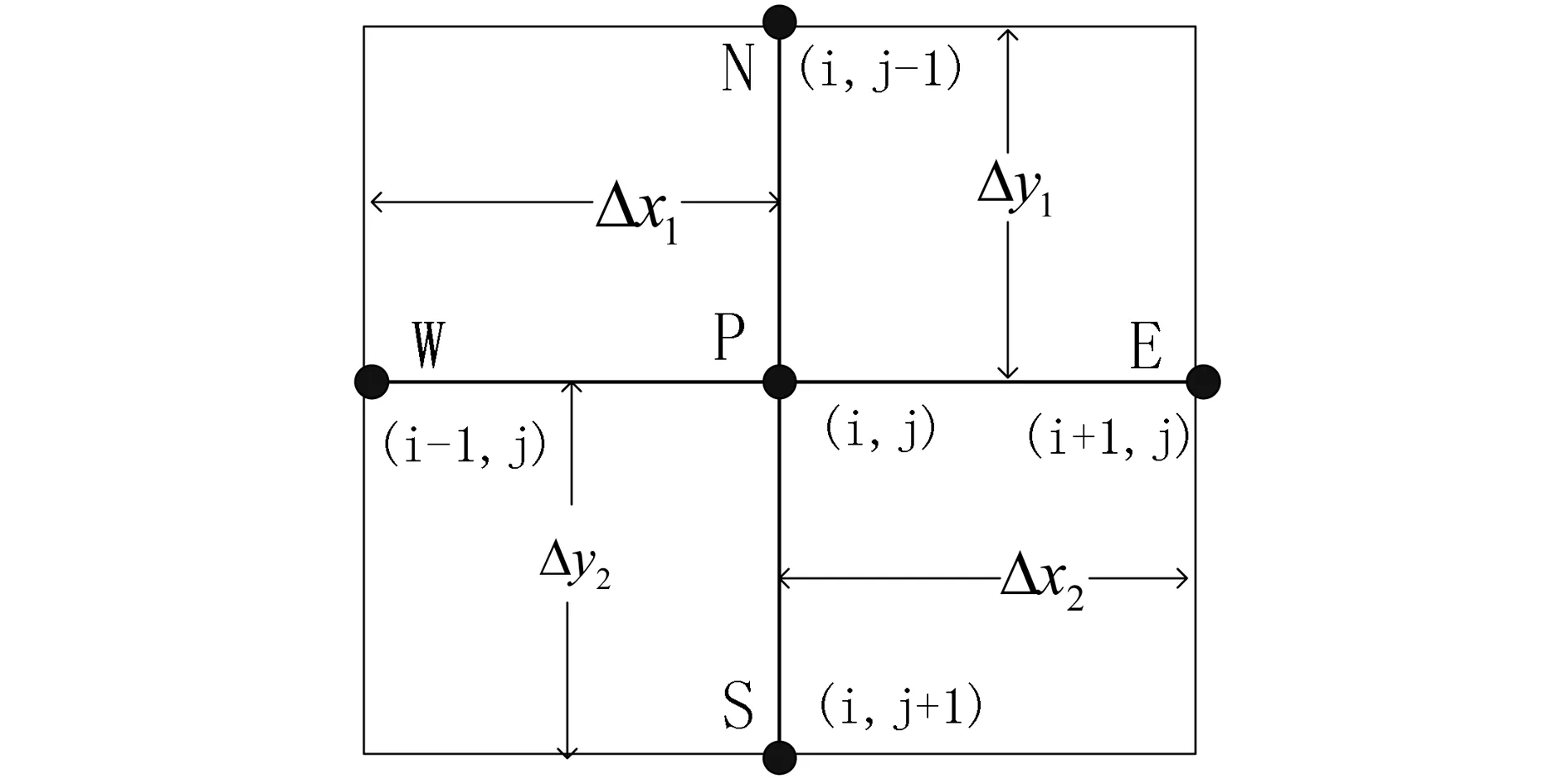
图1 直角坐标的网格系统

(1)

式中：ρ、Cp、K分别为材料的密度、比热及导热系数;T为电缆及土壤不同位置的温度;Q为热源。

传热学中边界条件可归纳为三类：第一类为已知边界温度；第二类为已知边界法向热流密度；第三类为已知界面上的流体温度和对流换热系数。计算中足够深度的土壤下边界为第一类边界，左右边界两条垂直线为第二类边界条件，地面土壤和地表空气层为第三类边界。

应用变步长离散导热方程为：

(2)

式中：i、j分别代表x、y坐标;T0代表上一时层的温度;Δt为离散的时间步长。式(2)可以进一步写成：

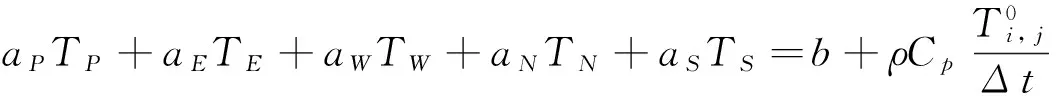
(3)

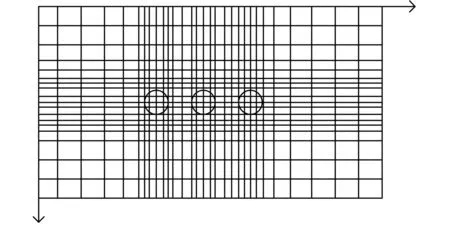
图2 电缆温度场不同区域网格划分

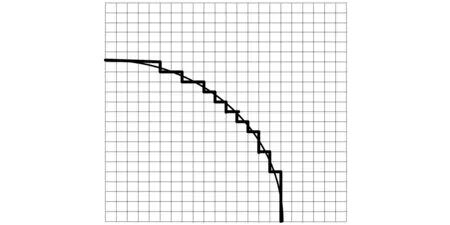
图3 电缆内部区域网格划分

1.2 电缆圆形边界的处理

适当的网格划分是计算电缆温度场中一个重要的前处理过程。梯形网格和不均匀网格可以简化编程，提高计算速度。如图2所示，整个计算区域分为加密区域和非加密区域，水平加密区域和竖直加密区域的交集为电缆所在区域。以电缆每一层作为划分对象，加密区域网格间距为2 mm，最后一个网格可以不足2 mm。若电缆某层厚度小于2 mm，以该层厚度作为网格间隔进行划分。非加密区域网格离电缆越远间距越大，可采用等比递加算法进行划分，间隔范围最大至200 mm。电缆附近温度梯度较大，采用加密网格提高了计算精度。离电缆较远的区域温度梯度较小，采用稀疏网格提高了计算速度。

在对物理问题作理论分析时，理想的坐标系是坐标轴与计算区域的边界相符合，称该坐标系是所计算区域的适体坐标系。矩形区域的适体坐标系是直角坐标系，圆形区域的适体坐标系是极坐标系。由于直角坐标系简单方便，在直角坐标系中进行复杂问题的数值计算较为容易便捷，电缆圆形边界采用如图3所示阶梯型网格进行划分[24]。阶梯型网格使圆形边界变为带直角尖峰的锯齿状粗糙边界，通过细化网格能够降低粗糙边界的影响。

2 方法验证

2.1 电缆稳态载流量计算结果比较

本文对单回和双回110 kV直埋电缆载流量进行了数值计算，验证了该方法在圆形边界处理上的正确性。采用交联聚乙烯绝缘电缆，铜线芯截面积为800 mm2，线芯最高允许温度为90 ℃。电缆平行敷设，其中双回电缆采用一字型排列，埋深为0.7 m，相邻相间的中心距离为0.2 m，铝护套采用三段交叉互联接地方式，每段为800 m。25 ℃时土壤热阻系数为1 K·m/W，空气和土壤的对流换热系数为12.5 W/(m2·K)，空气温度为40 ℃，土壤温度为25 ℃。在实际工程中，为了防止电缆敷设区域土壤发生形变而损坏电缆，在电缆周围回填砂土，回填土热阻系数为3 K·m/W。单回路时回填土区域横向0.8 m，纵向1.2 m(从地面到地下1.2 m)；双回路时回填土区域横向1.4 m，纵向1.2 m。在横向方向上，电缆位于回填土区域的中央。在相同的敷设条件下，分别采用文献[18]的坐标组合法与本文算法计算载流量，计算结果如表1所示。表1中I1为单回路载流量，I2为双回路载流量，δ为以坐标组合法为准则的本文算法计算载流量的相对误差。

从数学建模角度讲，模型对所研究问题的物理原型假设越少，模型误差越小。坐标组合法分别采用极坐标和直角坐标计算电缆内部和电缆外部温度场，避免了对电缆圆形边界的等效，计算结果较为准确。IEC方法假设电缆表面为等温面、电缆周围土壤温度相等、电缆放置在无限大媒质中以及土壤表面为等温线。本文方法采用阶梯形直线代替圆形曲线。所以，IEC和本文算法都会产生一定的模型误差。由表1可见，本文方法与坐标组合法的计算结果吻合。

表1 载流量计算结果比较

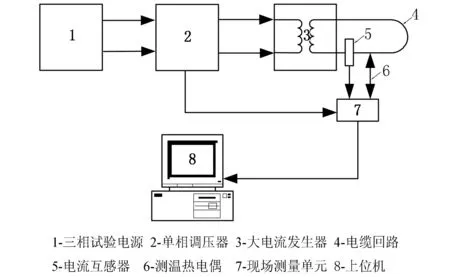
图4 电缆温升试验示意图

2.2 试验验证

2.2.1 恒定负荷电流温升试验

大电流试验是验证数值计算正确性最有效和最直接的方法。课题组在东北电力大学高电压与绝缘技术实验室外进行了66 kV直埋电缆大电流温升试验，试验验证了单芯电缆暂态温度场数值计算的正确性。

试验接线如图4所示，试验方法与文献[3]相似，通过电子测温系统实时测量线芯、铝护套、外护层表面和环境温度。试验电缆采用YJLW03-48/66 1×240，埋深为0.8 m，土壤热阻系数为2.44 K·m/W，密度为1 400 kg/m3，深层土壤温度为15.5 ℃。土壤比热容与导热系数kt关系为[25]：

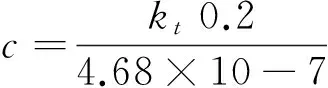
(4)

表2给出了66 kV电缆结构和参数。图5给出了电缆施加了168小时600 A的恒定电流的温升曲线。由图5中可见，数值计算结果与试验结果较为吻合，线芯计算温度和试验温度最大相差3.0 ℃，外护层表面计算温度和试验温度最大相差3.3 ℃。接近稳态时，线芯计算温度和试验温度相差0.11 ℃。

表2 电力电缆参数

图5 恒定负荷电缆温升试验

2.2.2 变负荷电流温升试验

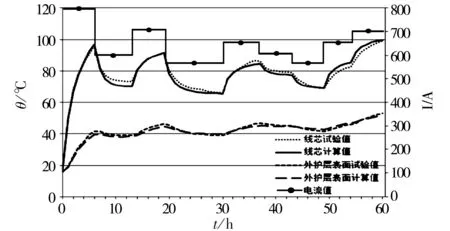
图6 变负荷电缆温升试验

图6给出了线芯电流阶梯状变化时，线芯和外护层表面温升试验测量值和数值计算值，试验持续时间为60 h。由图6可见，数值计算与试验较为接近，线芯计算温度和试验温度最大相差3.5 ℃，外护层表面计算温度和试验温度最大相差2.5 ℃。所以，本文所述数值计算方法可以计算任意负荷下的电缆暂态温升。

3 电缆载流量试验中热稳定判据及试验误差的研究

3.1 文献[3]单根电缆载流量试验结果分析

电缆载流量对电缆线路设计、敷设和运行都具有重要意义，试验是确定其值最有效和最直接的方法。载流量实际测定时，在电缆中通过恒定负荷电流。由于电缆本体和周围土壤热阻及热容的存在，电缆线芯温度逐渐升高并无限趋近于理论稳定状态。文献[3，4]在载流量试验研究中规定：当电缆线芯温度在4 h内升高不超过1 ℃时，电缆温升达到稳定状态。

文献[3]载流量试验研究中110 kV单根电缆直埋敷设如图7所示。电缆埋设深度1 m，回填土宽度0.8 m。回填土热阻系数0.819 K·m/W，母土热阻系数0.545 K·m/W。电缆结构参数见文献[3]中的表1。该电缆施加的恒定负荷为1 330 A，104 h内缆芯温升试验曲线和本文计算曲线如图8所示。由图8可见，本文计算结果与试验结果基本吻合，温升初始阶段最大相差约为5.5 ℃，100 h后最大相差约为1.0 ℃。

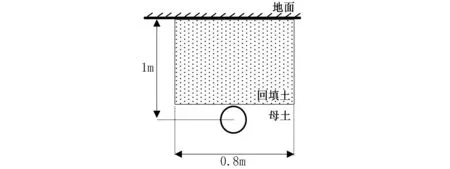
图7 电力电缆载流量试验布置图

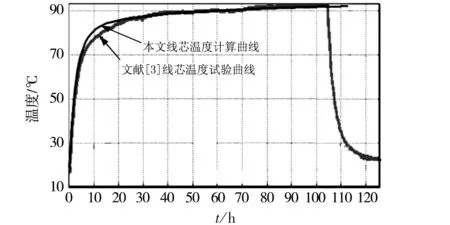
图8 单根直埋电缆温升曲线

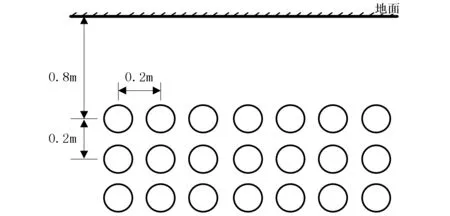
图9 电缆敷设示意图

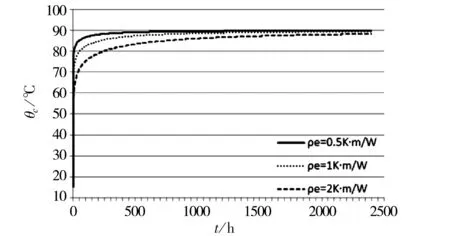
图10 不同热阻系数线芯温升曲线

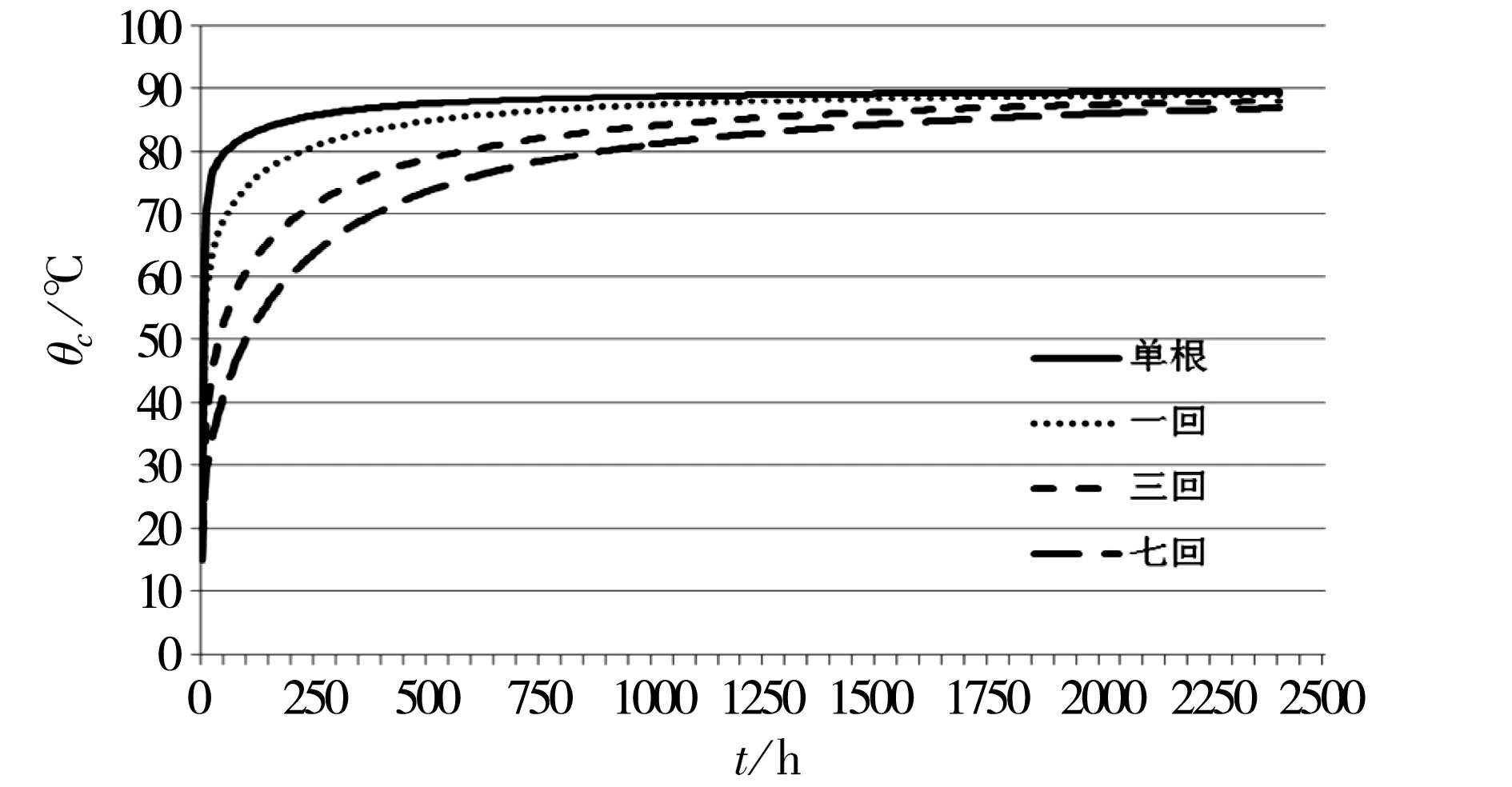
图11 不同电缆布置方式下的电缆线芯温升曲线

文献[3]建议电缆线芯4 h内温升≤1.0 ℃作为热稳定状态的判断标准，并依据图8的试验曲线认为104 h达到热稳定状态。针对该载流量试验，本文的数值计算结果表明：(1)电缆计算载流量为1 253 A。电缆线芯在1 330 A电流下100 h-104 h中的4 h温升仅为0.13 ℃，在104 h后的线芯温升为92 ℃，其后线芯温升十分缓慢，3 000 h后(视为最终稳态)温度为99.5 ℃，即试验结束后线芯尚可有7.5 ℃的温升。若1 330 A在104 h达到稳态温度92 ℃，则1 312 A在104 h达到90 ℃，此次载流量试验误差4.7%；(2)在恒定负荷载流量1 253 A，以4 h温升不大于1 ℃作为热稳定判据，热稳定时间为21 h，相应线芯温度为78 ℃，载流量试验误差为8.9%。

3.2 恒定负荷下电缆温升速度及影响因素的研究

采用热路方法分析电缆暂态过程，其热过程应为一链形网络，电缆及其周围媒质应是一分布参数，电缆线芯温升曲线并非单纯指数函数，而是多个指数函数的叠加。

本文采用上述电缆暂态数值计算程序，分析了均匀土壤中电缆在恒定负荷电流下土壤热阻系数和电缆根数对缆芯温升速度的影响。以66 kV/240 mm2直埋单芯交联聚乙烯电缆为例，土壤密度为1 400 kg/m3，深层土壤温度为15 ℃。单根、单回路、三回路和七回路电缆敷设条件如图9所示。计算时单根和单回路(横向排列)电缆位于图9中最上层，多回路电缆纵向排列，试验电缆间距均为0.2 m。

图10给出了当土壤热阻系数ρe分别为2.0 k·m/W、1.0 k·m/W和0.5 k·m/W时，直埋单根电缆在相应的载流量下2 400 h线芯暂态温升曲线。2 400 h时热稳定温度分别为88.8℃、89.6 ℃和89.9 ℃。图11给出了单根、单回路、三回路和七回路电缆在土壤热阻系数1.0 k·m/W的均匀土壤中，加载恒定负荷的载流量下2 400 h线芯暂态温升曲线，其中多根电缆为最热线芯温度。2 400 h时单根、单回路、三回路和七回路电缆的最热线芯温度分别为89.6 ℃、89.1 ℃、88.0 ℃和86.8 ℃。继续计算表明，三回路和七回路电缆在7 200 h时线芯的温度分别达到89.85 ℃和89.68 ℃。

由图10和图11可见，电缆系统温升速度随土壤热阻系数增大和电缆根数的增加而变慢。这是因为土壤热阻系数增加，导致土壤热阻增加和热容略有减小，热阻与热容的乘积增大；电缆根数增加时，电缆的热影响区域(即决定电缆系统温升过程的有效土壤区域)增大，相应的土壤热阻和热容增加，温升更加缓慢。

3.3 载流量试验热稳定判据及试验误差的研究

表3给出了本文试验所用电缆在不同敷设方式(ρe=1.0 k·m/W)和不同土壤热阻系数下(单根电缆)，计算载流量I、热时间常数τ和n小时线芯温升Δθn≤1℃为热稳定判据时，计算载流量下的线芯热稳定温度θc、试验载流量Is(视在热稳定点出现在90 ℃)及其试验误差δ和试验载流量下电缆到达视在稳态时间t。由表3可见:

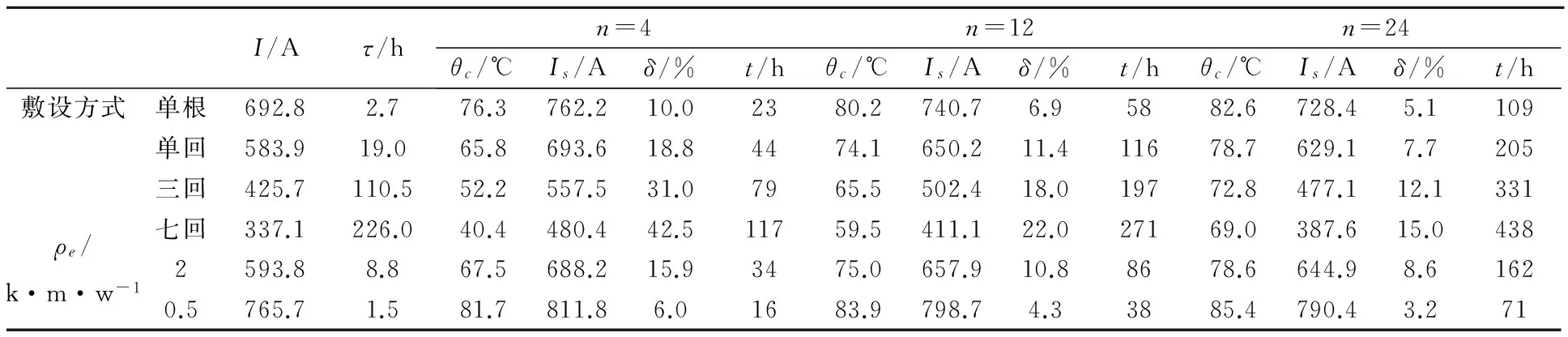
表3 均匀土壤中热稳定判据与载流量的测量误差

(1)热时间常数越小，即电缆温升速度越快，相同的热稳定判据下达到热稳定时间越短，试验误差越小；

(2)n小时线芯温升Δθn≤1 ℃为热稳定判据时，n越大试验时间越长，载流量试验误差越小；

(3)载流量计算值下线芯稳定温度θc与90 ℃的差异越大，载流量试验误差越大。采用Δθ4≤1 ℃作为热稳定判据，单根、单回路、三回路和七回路电缆达到稳态时最热线芯温度分别为76.3 ℃、65.8 ℃、52.2 ℃和40.4 ℃，载流量的试验误差分别为10.0%、18.8%、31.0%和42.5%；采用Δθ12≤1℃作为热稳定判据，单根、单回路、三回路和七回路电缆达到稳态时最热线芯温度分别为80.2 ℃、74.1 ℃、65.5 ℃和59.5 ℃，载流量试验误差分别降至6.9%、11.4%、18.0%和22.0%；采用Δθ24≤1 ℃作为热稳定判据，单根、单回路、三回路和七回路电缆达到稳态时，最热线芯温度分别为82.6 ℃、78.7 ℃、72.8 ℃和69.0 ℃，载流量试验误差分别降至5.1%、7.7%、12.1%和15.0%。所以，电缆根数越多，恒定负荷下温升越缓慢，采用Δθ4≤1 ℃作为热稳定判据的载流量试验误差越大；(4)土壤热阻系数分别为2 k·m/W，1.0 k·m/W和0.5 k·m/W时，采用Δθ4≤1℃作为热稳定判据，单根电缆达到热稳定时相应的线芯温度分别为67.5 ℃、76.3 ℃和81.7 ℃，载流量的试验误差分别为15.9%、10.0%和6.0%。而采用Δθ12≤1 ℃作为热稳定判据，达到热稳定时线芯温度分别为75.0 ℃、80.2 ℃和83.9 ℃，载流量试验误差分别为10.8%、6.9%和4.3%。采用Δθ24≤1 ℃作为稳定判据，达到热稳定时线芯温度分别为78.6 ℃、82.6 ℃和85.4 ℃，载流量试验误差分别为8.6%、5.1%和3.2%。土壤热阻系数越大，恒定负荷下电缆温升越缓慢，采用Δθ4≤1 ℃作为稳定判据的载流量试验误差越大。

4 结 论

本文采用阶梯型网格划分电缆圆形边界，只在直角坐标系中离散导热方程，编程简便且计算速度快。该方法可以准确计算任意复杂土壤条件下电缆暂态温度场，具有较高的工程实用价值。采用该程序计算恒定负荷电流下电缆暂态温升过程，计算结果表明：1)当土壤热阻系数的增大时，土壤热阻增加而热容略有减小，土壤热阻与热容乘积增大，电缆线芯温升变慢，热时间常数加大；2)当电缆根数增加时，电缆热影响区域增大，土壤的有效热阻和热容增加，电缆线芯温升变慢，热时间常数加大；3)若采用n小时温升Δθn≤1 ℃为热稳定判据，载流量试验可能造成的误差与电缆温升速度有关，电缆线芯温升速度越慢，载流量试验误差越大。目前载流量试验中Δθ4≤1℃的热稳定判据将可能造成较大的试验误差，增大n值可显著降低载流量试验误差。

[1] 娄娟，周天鸿，张光普，等.220kV电力电缆本体热阻特性的试验研究[J].东北电力大学学报，2013，33(1/2)：72-75.

[2] 雷成华，刘刚，阮班义，等.根据导体温升特性实现高压单芯电缆动态增容的实验研究[J].高电压技术，2012，38(6)：1397-1402.

[3] 刘刚，雷成华.提高单芯电缆短时负荷载流量的试验分析[J].高电压技术，2011，37(5)：1288-1293.

[4] 赵健康，雷清泉，王晓兵，等.复杂运行条件下交联电缆载流量研究[J].高电压技术，2009，35(12)：3123-3128.

[5] 汤毅，王晓兵，陈燕萍，等.10kV三芯交联电缆载流量的试验研究[J].高电压技术，2009，35(11)：2807-2812.

[6] 张尧，周鑫，牛海清，等.单芯电缆热时间常数的理论计算与试验研究[J].高电压技术，2009，35(11)：2801-2806.

[7] 马国栋.电线电缆载流量[M].北京：中国电力出版社，2003.

[8] International Electrotechnical Commission.IEC 60287-1.Calculation of current rating part 1:(100% load factor) and calculation of losses[S]，2001.

[9] 刘刚，雷成华，刘毅刚.根据电缆表面温度推算导体温度的热路简化模型暂态误差分析[J].电网技术，2011，35(4)：212-217.

[10] 鲁志伟，于建立，郑良华，等.交联电缆集群敷设载流量的数值计算[J].高电压技术，2010，36(2)：481-487.

[11] Gela G，Day J J.Calculation of thermal fields of underground cables using the boundary element method[J].IEEE Transactions on Power Delivery，1988，3(4):1341-1347.

[12] 梁永春，柴进爱，李彦明，等.基于FEM的直埋电缆载流量与外部环境关系的计算[J].电工电能新技术，2007，26(4)：10-13.

[13] GJ.Anders，M.Chaaban，N.Bedard.New approach to ampacity evaluation of cables in ducts using finite element technique [J].IEEE Transactions on Power Delivery，1987，2(4):969-975.

[14] 王有元，陈仁刚，陈伟根，等.有限元法计算地下电缆稳态温度场及其影响因素[J].高电压技术，2008，34(12)：3086-3092.

[15] 付永长，张文斌，陈涛，等.不规则排列电缆温度场及载流量计算[J].电网技术，2010，34(4)：173-176.

[16] M.A.Hanna，A.Y.Chikhani，and M.M.A.Salama.Thermal analysis of power cables in multi-layered soil Part 1:Theoretical model [J].IEEE Transactions on Power Delivery，1993，8(3):761-771.

[17] 郑良华，于建立，周晓虎，等.直埋电缆群载流量和稳态温度场计算新方法[J].高电压技术，2010，36(11)：2833-2837.

[18] 曹惠玲，王增强，李雯靖，等.坐标组合法对直埋电缆与土壤界面温度场的数值计算[J].电工技术学报，2003，18(3)：59-63.

[19] 鲁志伟，于建立，葛丽婷，等.管道内填充导热介质提高电缆载流量[J].高电压技术，2009，35(11)：2826-2831.

[20] Carlos Gaggido，Antonio F.Otero，and José cidrás.Theoretical model to calculate steady-state and transient ampacity and temperature in buried cables[J].IEEE Transactions on Power Delivery，2003，18(3):667-677.

[21] 于建立，常树生，牛远方，等.地下电力电缆温度场及载流量的数值计算[J].东北电力大学学报，2008，28(4)：62-65.

[22] 鲁志伟，马溯，李艳飞.直埋电缆载流量及稳态温度场新算法[J].中国科技投资，2012，33：61-62.

[23] 于建立，隋琳琳，田际平，等.基于有限容积的电缆群载流量计算和分析[J].东北电力大学学报，2012，32(4)：94-98.

[24] 陶文铨.数值传热学[M].西安：西安交通大学出版社，2007.

[25] H.J.Li，Estimation of soil thermal parameters from surface temperature of underground cables and prediction of cable rating.IEE Proc.-Gener.Transm.Distrib.，2005，152(6):849-854.

Research of Thermal Time Constant and Steady Criterion used in the Power Cables Ampacity Test

LU Zhi-wei1，ZHANG Hang1，AO Ming2，YU Hai3，LI Yan-fei4

(1.Elec.Eng.College，Northeast Dianli University， jilin，132012，China；2.The Research Institute of Jilin Electric Power Co.，Ltd.，Changchun，130021，China；3.State Grid Zibo Power Supply Company，Zibo，255000，China；4.Guangzhou Power Bureau of Guangdong Power Grid Company，Guangzhou，510620，China)

The conductor temperatures of power cables change with load current as well as thermal characteristic parameters of power cables and surrounding medium.For the safety and the economy of transmission，it is meaningful to accurately predict the transient state thermal field of underground cables.Determining conductor temperatures is the basis of improving the current-carrying capacity.The finite difference method has shown difficulty in dealing with circular boundary of power cables and rectangular boundary of the surrounding soil when calculating temperature field of power cables.In this paper，ladder straight lines are adopted to substitute circular boundary of power cables，and temperature fields as well as ampacity are solved in Cartesian coordinate system.Numerical calculation results of finite difference method，which are based on the combinatorial coordinate and the temperature rise tests of the constant as well as variable load current，have proved that the method presented in this paper is effective to calculate the temperature fields of underground cables.The ampacity of power cables is often determined by experimental test.The present experimental ampacity，and the temperature rise of power conductors of constant load current，are studied based on the method presented in this paper.The results show that the temperature rise speed of power conductors slows when the soil thermal resistivity and the power cables increase.The tested ampacity may be much higher than the real ampacity because of the thermal steady criterion used in the test.

Power cables；Transient temperature field；Finite difference method；Ampacity test；Thermal steady criterion；Test error

2016-04-12

吉林省科技发展计划项目(20130101071JC)，吉林省电力有限公司科技项目(2013-39)

鲁志伟(1963-)，男，吉林省吉林市人，东北电力大学输变电学院教授，博士，主要研究方向：接地技术，电力电缆运行和电介质材料.

1005-2992(2016)05-0025-07

TM76

A