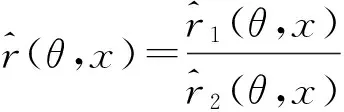单函数指标非参数回归估计的一致几乎完全收敛
伍雪洁, 许 谦, 凌能祥
(合肥工业大学 数学学院,安徽 合肥 230009)
定义1(α混合的定义) 过程{(Xi,Yi),i≥1}被称为α混合或者强混合,且混合系数为α(n),如果
单函数指标非参数回归估计的一致几乎完全收敛
伍雪洁, 许 谦, 凌能祥
(合肥工业大学 数学学院,安徽 合肥 230009)
文章研究了单函数指标非参数回归模型的估计问题,利用Kolmogorov熵的方法,基于时间序列函数型数据,在α混合相依序列下,获得了模型中非参数回归函数算子核估计的一致几乎完全收敛及其收敛速度,推广了现有文献中的相关结果。
单函数指标模型; 时间序列函数数据;Kolmogorov熵;一致几乎完全收敛速度
随着计算机的快速发展和信息技术的不断进步,在自然科学、工程技术及人文社科等诸多领域所收集到的观测数据具有函数特征,常常称之为函数型数据,如不同地区的多期降雨量曲线数据、用电负荷量曲线数据等。因此,函数型数据被看作是连续时间随机过程的一条样本轨道。关于函数型数据分析及应用参见文献[1-2],而有关非参数函数型数据的统计推断参见文献[1]。
另一方面,由于单指标模型在非参数回归中处理高维数据问题是非常有用的,被许多学者广泛研究过。通常情况下,在多维非参数回归中模型是将多维的解释变量X引入一个单指标参数向量θ,利用θTX形成一元指标,不仅大大降低了维数,而且还能够抓住高维数据的本质特征,所以它早已被广泛地研究和应用,例如文献[3]通过选取适当的窗宽对单指标模型参数做了最优估计;文献[4]利用迭代的方法对单指标模型如何选择参数系数进行了改进。
最近,基于单函数型指标模型的非参数统计推断受到很多学者的关注。文献[5]构建了固定参数θ下单函数型指标模型;文献[6]给出了独立样本下,单函数型指标模型中条件密度函数非参数估计量的收敛速度;文献[7]研究了固定单指标参数时,基于α混合函数型数据,获得了非参数回归函数算子的逐点收敛;文献[8]采用交叉验证的方法对单函数指标模型参数θ进行了估计;文献[9]给出了单指标模型在α混合条件下条件密度函数及条件众数的几乎完全收敛速度;文献[10]证明了单指标参数固定时,单指标模型在α混合条件下条件密度函数和条件众数的渐近分布。
受上述研究文献的启发,本文利用Kolmogorov-ε熵的方法,进一步研究了基于α混合相依函数型时间序列数据时,单函数型指标模型非参数回归函数算子估计问题,在一定条件下获得了估计量的一致几乎完全收敛速度,推广了文献[7]中的相关结果。
1 模 型
定义1(α混合的定义) 过程{(Xi,Yi),i≥1}被称为α混合或者强混合,且混合系数为α(n),如果

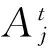
本文首先假设{(Xi,Yi),1≤i≤n}为同分布于(X,Y)的α混合函数型序列,且混合系数α(n)满足∃C>0,α(n)≤Cn-a,参数a>0。其次, 假设Xi、X取值于Hilbert空间H,且其内积是〈·,·〉;Yi、Y取值于实数空间R1。另外,类似于文献[5]的模型,本文通过一个确定的函数型指标θ(θ∈H)来构造Y关于X的条件期望,即
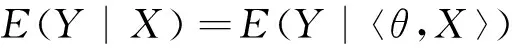
(1)
关于(1)式模型的进一步介绍,可以参考文献[5-6,8]。
一般地,为了通过函数型变量X来预测响应变量Y,基于非参数回归算子r为

(2)
利用文献[1]的思想,类似地建立回归函数r(x)的非参数核估计如下
(3)
其中,K为核函数;窗宽h=hn为正的实数序列,并且当n→∞时,h→0。
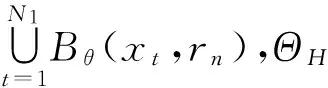
令Nε(SH)为H中覆盖SH所需要的半径为ε的开球的最小个数时,数量
(4)
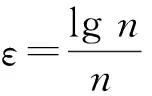
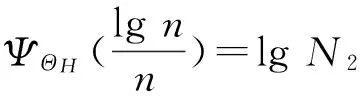
2 基本假设和主要结果
为了叙述方便,首先引入几个记号,对于∀x∈SH,有
另外,记
其中
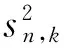
本文中出现的C为正常数,它在不同的情形可以取不同的值。
为了给出本文的主要结果,作如下基本假设。
H1 ∀x∈SH,存在函数φθ,x(·),有P(X∈Bθ(x,h))=φθ,x(h),当h→0,φθ,x(h)→0。
H2 核函数K在支撑集[-1,1]非负有界。
H3 ∃β>0,对于∀(x1,x2)∈SH×SH,回归函数r满足|r(θ,x1)-r(θ,x2)| H4 ∃b>2,a>1,有 当n充分大时,SH、ΘH的Kolmogorov熵ΨSH、ΨΘH满足: (3)nφθ,x(h)=O(lg2n)。 H1、H2为非参数函数型数据分析中的常见假设,参见文献[1];H3为刻画回归函数的连续条件,参见文献[7];H4类似于文献[9-10]的假设,是给出在相依条件下的协方差结构;H5为构造收敛速度的技术性条件,参见文献[9]。 本文的主要结论如下。 定理1 在假设H1~H5下,当n→∞,有 (5) 推论1 在定理1的条件下,对于固定的θ0,则有 2017年的春节,位于中蒙边境的独立营三连家家户户张灯结彩,汉族职工与哈萨克族职工就像一家人一样一起吃着团圆饭,喝着额河酒,边吃边唱其乐融融,这样的春节聚会在这个连队已经延续了十几年,这样各民族亲如一家,和谐共融的连队在这个团场还有14个。自2016年“民族团结一家亲”活动开展以来,一八三团举全团之力打造“123456示范工程”,创建“民族团结一家亲”先进集体,“各民族都是一家人,一家人都要过上好日子”成为团场各民族职工群众的共同信念。 (6) 文献[7]研究的是在固定的θ0下回归函数的逐点收敛,而推论1是在固定的θ0下回归函数的一致收敛。 事实上,类似于文献[1]的思想,有如下的分解式 (7) 其中 引理1 在条件H1、H2、H4、H5下,当n→∞时,则有 (8) 证明 类似于文献[9]的思想,有如下的 (9) 首先考虑A3。对于ε0>0,有 根据文献[1]中的命题A.11(ii)及Kolmogorov熵的定义,取r=lg2n以及q=a+1,由H1、H5)(1)(3)有: (10) (11) 这里,一方面,∃η>0,满足b>b-η>2;另一方面,由H5(1)(3)可得: (12) 于是,有 (13) 由(13)式和条件 H5(2),即得: (14) 考虑A1,在条件H1、H2下,有 (15) 类似于A3的证明,可得: (16) 另外,由于A4≤A2,A5≤A1。因此,当n→∞时,也有: (17) 综上所述,由(9)式、(14)式、(16)式和(17)式,引理3成立。 引理2 如果假设H2、H3满足,当n→∞时,有 (18) 证明 因为 在假设H2、H3下,有 所以引理2成立。 引理3 在引理3的条件下,当n→∞,有 (19) 证明 在引理1中,取Yi=1,即能得到引理3成立,具体的证明过程省略。 根据引理1~引理3以及(7)式可证明定理1成立。 [1] FERRATY F,VIEU P.Nonparametric functional data analysis:theory and practice[M].New York:springer,2006. [2] RAMSAY J O,SILVERMAN B W.Functional data analysis[M].New York:Springer,1997. [4] HISTACHE M,JUDITSKY A,SPOKOINY V G.Direct estimation of the index coefficient in a single-index model[J].The Annals of Statistics,2001,29(3):593-623. [5] FERRATY F,PEUCH A,VIEU P.Modèle àindice fonctionnel simple[J].Comptes Rendus Mathematique,2003,336(12):1025-1028. [6] ATTAOUTI S,LAKSACI A,OULD-SAID E.A note on the conditional density estimate in the single functional index model[J].Statistics and Probability Letters,2011,81(1):45-53. [7] AIT-SAIDI A,FERRATY F,KASSA R.Single functional index model for a time series [J].Revue Roumaine de Mathematique Pures et Appliquees,2005,50(4):321-330. [8] AIT-SAIDI A,FERRATY F,KASSA R,et al.Cross-validated estimation in the single functional index model [J].Statistics,2008,42(6):475-494. [9] LING N X,LI Z H,YANG W Z.Conditional density estimation in the single functional index model for α-mixing functional data[J].Communications in Statistics: Theory and Methods,2014,43(3):441-454. [10] LING N X,XU Q.Asymptotic normality of conditional density estimation in the single index model for functional time series data[J].Statistics and Probability Letters,2012,82(12):2235-2243. [11] FERRATY F,LAKSACI A,TADJ A.Rate of uniform consistency for nonparametric estimates with functional variables[J].Journal of Statistical Planning and Inference,2010,140(2):335-352. (责任编辑 张 镅) Uniform almost complete convergence of nonparametric regression estimate in single function index model WU Xuejie, XU Qian, LING Nengxiang (School of Mathematics, Hefei University of Technology, Hefei 230009, China) In this paper, the estimation of nonparametric regression in single function index model is investigated based on time series functional data by the Kolmogorov's entropy. With theαmixing dependent sequence, the uniform almost complete convergence rate of the kernel estimation of nonparametric regression function is obtained, extending the related results of the existing literature. single function index model; time series functional data; Kolmogorov's entropy; uniform almost complete convergence rate 2013-02-12; 2015-11-20 安徽省自然科学基金资助项目(11040606M03) 伍雪洁(1988-),女,安徽阜阳人,合肥工业大学硕士生; 凌能祥(1964-),男,安徽合肥人,合肥工业大学教授,硕士生导师. 10.3969/j.issn.1003-5060.2016.09.027 O212.7 A 1003-5060(2016)09-1292-05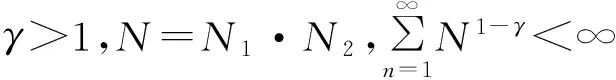
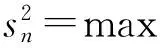
3 若干引理及证明