蓬莱19-3溢油运移与归宿数值模拟和分析
匡翠萍, 谢华浪, 苏 平, 陈 括
(1. 同济大学 土木工程学院, 上海 200092; 2. 广西壮族自治区交通规划勘察设计研究院, 广西 南宁 530029)
蓬莱19-3溢油运移与归宿数值模拟和分析
匡翠萍1, 谢华浪1, 苏 平2, 陈 括1
(1. 同济大学 土木工程学院, 上海 200092; 2. 广西壮族自治区交通规划勘察设计研究院, 广西 南宁 530029)
通过耦合水动力模型建立渤海海上溢油运移与归宿数学模型,包含漂移、扩散、蒸发、乳化等过程,通过拉格朗日方法模拟漂移过程、蒙特卡罗方法模拟油粒子扩散的随机性,采用变化的紊动扩散系数使溢油所受紊动扩散作用随时间变化.通过率定得到蓬莱19-3溢油模拟中风拖拽系数和扩散系数校正参数b的合理取值范围分别为1.4%~2.3%和0.38~0.42.对蓬莱19-3溢油事故进行了模拟,通过溢油附岸位置与时间验证了模型的准确性.模拟结果表明: 由于风速较大、方向变化较小,风对漂浮于水面上的溢油产生较大作用,且溢油漂移方向与主风向一致;渤海海域内的潮流以往复流、旋转流为主且余流小使其对溢油运移的作用弱于风;溢油初期的蒸发速度较快,后期因挥发组分的减少以及乳化作用使溢油含水率增大使得蒸发速度明显减小;蒸发和附岸是溢油漂浮组分减少的主要原因,也是溢油的主要归宿.
渤海; 海上溢油; 运移; 数值模拟
目前,海上石油污染已成为一种全球性海洋污染[1].海上溢油以其突发性、污染的严重性以及应急处理的艰巨性使其在过去的几十年里成为海洋生态环境最大的破坏因素,且呈现越来越严重的趋势[2].尤其当溢油事故发生于近岸或河口水体环境时,被污染的水体及近岸环境将受到惨重的破坏[3].2011年渤海蓬莱19-3溢油事故造成了极其恶劣的环境破坏,海水污染面积高达4 900 km2,造成的海洋生态损害价值总计16.83亿元[4].根据康菲公司公布数据,本次事故溢油量为500 t,然而多数研究学者认为实际溢油量甚至高达该数据的十倍以上[5].
海上溢油属于突发性的海洋污染事故,且传播速度快、影响范围大.但由于海洋环境复杂多变,溢油事故发生于不同的时间和地点都可能产生不同的漂移轨迹和污染范围[6].因此,对海上溢油进行数值模拟,有利于预测溢油变化趋势,制定合理的治理方案,及时采取应对措施,最大程度地减少溢油事故带来的破坏和损失.徐青等[7]通过GNOME导入潮流和风建立了渤海溢油模型,通过将溢油油膜概化为由多数圆形斑点组成,并采用拉格朗日方法模拟了渤海蓬莱19-3溢油事故6月11—19日中部分油膜的漂移过程.邓增安等[3-6]考虑了风、潮流、波浪等因素,研发了嵌套于中国数字海洋原型系统(CDOPS)中的BSOSSM溢油模拟服务组件,并对蓬莱19-3溢油事故进行了模拟.汪守东[8-9]与王金华等[10]将海上溢油分为表层浮油和悬浮油滴,通过离散颗粒的拉格朗日算法进行计算,考虑了溢油的漂移、扩散、蒸发和乳化等过程,建立了渤海海域溢油模型.毕海普等[11]建立了三峡水库溢油模型,通过在模型中设置一个衰减参数来模拟与分析三峡水库溢油事故发生后各溢油组分在机械回收和投放分散剂、乳化剂等紧急措施影响下的变化情况.李燕等[12]建立了三维的拉格朗日随机步溢油模型,并研究了在不同方案下油粒子垂直扩散的变化情况.总体来说,目前各种溢油模型所采用方法与考虑因素各有不同.其中,对溢油的漂移过程模拟均采用拉格朗日方法,计算中主要将风和潮流的作用作为溢油漂移的主要影响因素.半封闭的渤海海域中风对溢油漂移的影响是最重要的,一般认为风拖拽系数取值范围在1%~3%之间,但对渤海区域风拖拽系数的取值尚未有详细的讨论和研究.另外,多数溢油模型由于对模拟粒子数限制较大,以至于对大规模的溢油模拟未能形成一个较为直观的溢油平面密度分布场.
利用Delft3D通过对水动力模型进行耦合建立了渤海海上溢油模型,模型计算包括漂移、扩散、蒸发、乳化等变化过程.本模型将溢油作为离散化的油粒子,通过拉格朗日方法模拟漂移过程、蒙特卡罗方法模拟湍流扩散过程,且采用随时间变化的紊动扩散系数使溢油所受湍流作用亦随时间变化,使得大规模的涡流和环流对溢油的扩散作用得以体现出来,并采用大量的油粒子进行模拟使溢油分布密度具有较高分辨率,对于判断不同区域的污染程度差异更为清晰直观.通过模型率定得到了风拖拽系数和扩散系数校正参数b的合理取值范围,在此基础上对2011年蓬莱19-3溢油事故进行了验证模拟,研究了渤海海域风和潮流对溢油运移的影响,并分析了溢油归宿的变化特征.
1 数学模型
1.1 Delft3D-FLOW水动力模型
FLOW模型的基本方程为二维或三维的非线性浅水方程,采用浅水假定和布西奈斯克(Boussinesq)近似由不可压缩流体的三维Navier-Stokes方程推求得出.由于垂向加速度远远小于重力加速度,故在垂直方向上的动量方程中忽略了垂直加速度的影响,并由此推导出在静压假定下的水流方程[13].平面二维水动力模型的基本方程为
(1) 连续方程

(1)
式中:ζ为水位;d为基准面下的深度,总水深H=d+ζ;u和ν分别表示水平方向上ζ和η向的流速分量;Gξξ和Gηη分别为正交曲线坐标系和Cartesian坐标系之间的转换系数;Q为单位面积的源汇项.
(2) 动量方程
ξ方向的动量方程
(2)
η方向的动量方程
(3)式中:ξ和η为平面曲线坐标;f=2Ωsinφ,为科氏力参数,由地球自转角速度和纬度值决定;ρ0为水的密度;Pξ和Pη为压力梯度;Fξ和Fη为水平雷诺应力的不平衡性;Mξ和Mη为外来源汇项引起的附加动量.
1.2 Delft3D-PART模块
Delft3D-PART模型是一个包含随机运动的粒子追踪模型,它将溶解或悬浮于水中的物质通过一定数量离散的油粒子来表示,每个油粒子代表一定质量的溢油.油粒子的运动包括漂移与扩散.漂移主要由流和风的作用引起;扩散则主要由湍流引起[14].本溢油模型计算还包括蒸发和乳化等变化过程.
1.2.1 漂移
漂移包括平流与风的拖拽产生的移动.每一个油粒子的平流速度通过所在计算网格节点的速度(由潮流模型获得)线性内插得到.风的拖拽计算中,风的影响仅仅作用于溢油,而对流场不再产生影响.风的拖曳作用,即将溢油因风产生的速度增量表达为风速的百分比进行计算,其关系见式(4).漂移过程通过拉格朗日方法进行模拟,其表达式如式(5)所示.
(4)

(5)

1.2.2 扩散
在释放粒子后的初始阶段,粒子团相对较小,这时粒子的扩散作用只是由小规模的湍流作用引起.当“粒子云团”充分扩散开来,大规模的涡流将对粒子的扩散产生明显的影响.故本模型采用随时间变化紊动扩散系数D,使得模拟溢油所受湍流过程亦随时间变化,以更好地模拟大规模涡流和环流对后期溢油的扩散作用.紊动扩散系数D的幂函数表达式为
D=atb
(6)
式中:t为时间,以粒子释放时间为初始时刻(t=0);a和b为紊动扩散系数的校正参数,且0 湍流扩散是在水动力速度场的基础上使油粒子产生一个附加位移.这个附加位移的方向是随机选取的,通过蒙特卡罗方法来模拟.蒙特卡罗方法即利用计算机通过构造符合一定规则的随机数以模拟随机现象进行近似计算的方法.在紊动扩散的过程中,其随机性的模拟基于一个白噪声过程,其随机数的取值范围为-1~+1,且均值为0.每个油粒子在一个时间步长Δt内的扩散位移为 (7) 式中:ΔS为单位时间步长的扩散位移;R为随机数,取值范围为[-1,1]. 1.2.3 蒸发 PART溢油模型将溢油分为挥发组分与不挥发组分,不挥发组分不发生蒸发过程,挥发组分将产生一阶衰减的蒸发过程.表达如下: (8) 式中:Fvol为挥发组分分数;Fv为已经蒸发掉的组分分数;k为蒸发率. 1.2.4 乳化 乳化过程本身是相对快速的,在实验室中乳化过程从发生到乳化完成大约需要0.1~3 h[15].但形成油包水乳化物的最长时间一般在10~100 h之间,这主要是因为溢油发生后往往要经过一段时间乳化作用才逐渐发生.乳化几乎是一个不可逆转的过程,它使溢油变为密度较大、具有高粘度的半固体物质.乳化过程根据Mackay等人[16]所提出的算法进行计算,其吸水率为 (9) 乳化过程不仅起到改变粘度的作用,它还将影响到溢油的蒸发过程和水下分散过程.根据Fingas[17]的研究,乳化过程能够使溢油粘度增大2~3个数量级,溢油扩散到水体中的过程减慢,而蒸发过程将近停止.为了使乳化过程和蒸发过程之间形成关联,计算中乳化物的含水率的增大将减小蒸发率,模型通过减小溢油中蒸发组分的大小来实现,相应的计算公式如下: (10) 式中:Fvol为乳化发生前溢油的蒸发组分;Few为乳化发生后溢油的蒸发组分.当乳化物达到最大含水率时,Few取值为0,蒸发过程终止. 1.2.5 附岸 附岸过程即溢油粘附于岸边并不再进入水体的过程.当溢油进入近岸海域后将发生附岸过程,并对海岸生态环境造成一定的破坏.本模型通过设定一个粘附概率进行模拟.当油粒子进入岸边或沉至床底时会获得一个介于0~1之间的一个随机数,当随机数小于粘附概率时则油粒子粘附于岸上并不再参与计算. 本模型计算范围为以大连—烟台为开边界的整个渤海海域,采用正交曲线网格,网格尺度约为1 000 m.计算网格与边界如图1所示. 图1 计算区域与网格 2.1 水动力模型及验证 水动力模型通过环渤海多个测站的潮位潮流资料进行了验证.以下仅列出2011年5月20—21日秦皇岛与山海关的潮位验证如图2和图3所示,以及2011年5月20日11点~21日11点V01和V10测站的潮流验证(图4). 图2 秦皇岛潮位验证(2011-05-20—21) 图3 山海关潮位验证(2011-05-20—21) 图4 V01和V10潮流流速流向验证 (2011-05-20 11:00—5.21 11:00) 采用Willmott[18]的统计学方法对水动力模型计算结果进行效率评价,计算公式如下: (11) 图5与图6分别为2011年6月4日涨急时刻与落急时刻渤海流场图.渤海湾、辽东湾和莱州湾潮流以往复流为主,渤海湾涨落潮流以W—E向为主,辽东湾涨落潮流以NE—SW向为主,莱州湾涨落潮流以SW—NE向为主,近岸海域由于岸线影响复杂多变.渤海中北部以旋转流为主,潮流流向呈顺时针旋转,涨落潮流向以NW—SE向为主.秦皇岛海域的潮流具有明显的往复流特征,涨、落潮方向与岸线平行,涨潮方向为西南方向,落潮方向为东北方向,涨、落潮平均流速均较小,并且差别不大.空间分布上,不同海域涨落急时刻并不同步,在三大海湾内涨落潮流速变幅较大,而渤海中部区域宽阔,流速变幅较小,秦皇岛海域处于无潮点附近,潮流流速变幅更小.总体上一个潮周期内渤海的余流较小. 图5 2011年6月4日涨急时刻流场 图6 2011年6月4日落急时刻流场 2.2 溢油模型 溢油模型将溢油概化为大量的油粒子,每个油粒子代表一定质量的溢油, 在拉格朗日方法的基础上增加了蒙特卡罗法计算溢油扩散随机性.根据国家海洋局调查报告[4],蓬莱19-3(图1)溢油事故发生于2011年6月4日,6月21日基本控制溢油,之后较长时间内仍有少量溢油溢出.2011年7月中下旬在东戴河岸滩发现长约4 km,宽约0.5 m呈不均匀带状分布的油污带;在昌黎黄金海岸岸滩高潮线附近发现长约1.2 km零星分布的油污带;在河北唐山浅水湾岸滩高潮线附近发现长约500 m,宽约1~1.5 m呈带状分布的油污带,低潮线附近有长约300 m,宽约1.5~2 m的油污带.即蓬莱19-3溢油最终在7月中下旬进入东戴河至浅水湾沿岸一带.根据溢油最终附岸的时间与位置对模拟结果进行验证. 2.2.1 基本参数设置 模拟对象为2011年蓬莱19-3溢油事故,作为连续溢油进行考虑,溢油释放时间为6月4日—7月31日,溢油总量为500 t,总粒子数为50 000个.溢油密度参数采用了蓬莱19-3油田中未熟-低熟油密度值(935 kg·m-3)[18].具体参数设置如表1所示,其中蒸发率为每天的蒸发部分所占比例. 表1 模型参数设置 2.2.2 风拖拽系数、扩散系数校正参数b率定 溢油运动包括漂移与扩散两部分:漂移主要由风应力和潮流引起,其中风应力起着非常关键的作用;扩散主要为紊动扩散,在初始阶段由小规模的湍流作用引起,当粒子“云团”充分扩散开来后,大规模的涡流将对粒子的扩散产生明显的影响.紊动扩散所引起的附加位移方向是随机的,可用随机扩散作用来模拟.在溢油数值模拟中,风拖拽系数和扩散系数对溢油的运移与扩散起着关键性的作用.不同的石油具有不同的组分和性质,同一环境条件下性质不同的溢油在漂移、扩散等变化过程中也会呈现出不同的结果.对于不同性质的溢油,其风拖拽系数和扩散系数是时空变化的,但是在一定的范围内变化需要通过率定确定. 由于风在溢油的漂移当中起着最重要的作用,风拖拽系数的大小对于溢油模拟的准确性也非常关键.在以往经验当中,风拖拽系数一般在1~3%之间进行取值,根据不同的溢油性质进行选择和校准[14].为了探索渤海风拖拽系数的合理范围,本次研究设置了不同的风拖拽系数,根据溢油的附岸时间与实际情况进行比较来确定.从图7可以看出,在6种风拖拽系数下的模拟结果均与实际情况较为接近,当Cωd=1.4%~2.3%时,溢油在7月中下旬进入东戴河至浅水湾沿岸一带,与实际情况较为相符;而当Cωd=1.1%、Cωd=2.6%时,溢油略微偏早或偏晚进入近岸海域.在适当范围内对风拖拽系数进行取值对于溢油的漂移路径没有太大影响;而由于较大的拖拽系数下溢油的漂移速度较快,在漂移相同的距离下向两边扩散的范围较小,故溢油的分布形状较为狭长.根据模拟结果与实际情况的对比,对密度大、粘度高的蓬莱19-3溢油进行溢油模拟时,风拖拽系数应取1.4%~2.3%.以下蓬莱19-3溢油模拟计算中风拖拽系数取值为Cωd=2%. b Cωd=1.4% c Cωd=1.7% d Cωd=2.0% e Cωd=2.3% f Cωd=2.6% 紊动扩散系数式(6)中含两个可变参数a和b.根据式(6)可知:参数a的影响较小,可取默认值1.0;对于时间跨度较长的溢油模拟,参数b起主要作用.本文主要针对参数b的影响进行探讨,通过设置不同的参数b进行模拟与对比,根据溢油的附岸范围和实际情况进行比较以确定合适的参数范围.模拟结果如图8所示,结果表明:参数b的改变对溢油的漂移速度和路径影响不大,对溢油的扩散范围影响较大.当b=0.38~0.42时,溢油于东戴河至浅水湾沿岸一带附岸,与实际情况相符;当b=0.3,0.35时,浅水湾沿岸未出现溢油附岸,溢油扩散范围偏小;当b=0.45时,溢油附岸范围两端分别略微超出了东戴河与浅水湾,扩散范围偏大.因此,在利用本模型对密度大、粘度高的蓬19-3溢油进行模拟时,参数b合理的取值范围为0.38~0.42.以下蓬莱19-3溢油模拟取b=0.4.经计算,时间步长设为1 h,则1 h后紊动扩散系数D=26.5,则最大扩散位移ΔS=756 m;24 h后D=94.3,则ΔS=1 427 m;10 d后D=236.9,ΔS=2 262 m;50 d后D=451.0,ΔS=3 122 m.模拟期间紊动扩散系数取值大概在26.5~500范围内.由于扩散位移的方向是随机选取的,故扩散位移主要使扩散范围逐渐增大,对溢油质心位移的影响较小.可见,溢油后期的紊动扩散系数增大,油粒子的扩散位移也明显增大.这样大涡促使溢油后期迅速扩散的作用便得以体现出来. a b=0.3 b b=0.35 c b=0.38 d b=0.4 e b=0.42 f b=0.45 模拟采用风场由美国NOAA提供的9个渤海及临近区域站点的风场数据,其中渤海中部站点(120°E,39.047°N)的风速风向如图9所示,平均风速为4.10 m·s-1,最大风速为12.04 m·s-1;常风向为南向,南向风占总数的25.4%,平均风速为5.02 m·s-1;南偏东、南、南偏西风向占总数的57.3%,平均风速为4.61 m·s-1. 在前面参数率定(即风拖拽系数Cωd=2%、扩散系数校正参数b=0.4)的基础上,对蓬莱19-3溢油事故进行模拟,结果如图10.溢油发生后扩散范围逐渐增大,前端扩散面积较大,平面分布密度较小,约为0.000 02 kg·m-2.溢油平台周围及其北偏西方向溢油分布密度较大,大约为0.000 05~0.000 5 kg·m-2.结合图9与图10进行分析可知:6月22日以前以南风为主,溢油运移方向与风向大致相同为正北方向;6月22日—7月4日,风向以东南偏东向和南向为主,溢油逐渐转为向西北方向运移,并靠近西北沿岸一带;7月4日—7月16日,风向以南向为主,溢油往北运移进入东戴河至黄金海岸沿岸一带;7月16日—7月22日,风向以南偏东向为主,溢油往西北方向运移,附岸范围向南扩展至浅水湾沿岸;随后风向以南向为主,溢油扩散范围略微往北偏移.总体上,溢油油污于7月中下旬进入浅水湾至东戴河沿岸一带,其中东戴河与黄金海岸沿岸一带受到的溢油污染最为严重,浅水湾受到的污染较轻,模拟结果与实际情况相符. 渤海海域夏季以南风和东南风为主,风速较大且风向较为稳定,溢油的漂移方向与主风向大致相同,表明风对漂浮于水面上的溢油的运移起着很明显的作用.然而,渤海海域的潮流流速不大,尤其是秦皇岛海域处于无潮点区域,潮流流速更小.渤海潮流以往复流和旋转流为主,涨潮潮流与落潮潮流流向大致相反,且流速差异不明显.一个潮周期内溢油在涨落潮流的作用下会来回摆动,余流小、净位移小.因此,在渤海海域内潮流对溢油的漂移不及风的作用. 图9 风速风向过程 (2011-06-04—7.31) a 6月14日 b 6月24日 c 7月4日 d 7月14日 e 7月24日 f 7月31日 溢油模型计算过程中,溢油主要分为漂浮组分、蒸发组分和附岸组分.图11为整个溢油模拟过程中各组分的质量变化图.其中溢油总量设定为线性增长,16 d(6月19日)基本控制溢油,溢油总量达290 t;后期依然持续有少量溢油溢出.在溢油前期,溢油漂浮组分和蒸发组分占溢油总量的绝大部分.漂浮组分在初始阶段随着溢油的发生呈线性增长,36 d(7月10日)达到最大值204 t,约占溢油总量的50.2%.之后随着漂浮于水面的溢油逐渐发生蒸发与附岸使其逐渐下降,第56 d(7月31日),漂浮组分下降至约155.0 t,占溢油总量30.6%.溢油的蒸发主要发生于溢油初期,由于前25 d溢油量较大,故蒸发量增长较快,于第25 d便达到约160 t,约占溢油总量48.2%;之后随着溢油挥发组分减少,且乳化过程使溢油含水率增大,使得蒸发在溢油的后期阶段速度减缓,第57 d(7月31日)蒸发量达到最大值约为223 t,占溢油总量的44.0%.其中,第22 d(6月26日)出现了12.04 m·s-1的最大风速,溢油的蒸发出现了短暂的陡增,漂浮组分也随之出现骤减,可见风对促进溢油蒸发也有一定作用.至第35 d(7月9日)之后,溢油进入沿岸海域并逐渐发生附岸,于7月31日达126 t左右,占溢油总量的24.9%. 图11 溢油组分质量变化图 通过Delft3D中的FLOW模块建立了渤海水动力模型,在水动力模型的基础上利用PART模块耦合建立了渤海海上溢油模型.率定了该溢油模型中风拖拽系数、扩散系数校正参数b的合理范围,对2011年蓬莱19-3溢油事故进行了模拟与验证,并对溢油运移与归宿进行了相关探讨.得出以下结论: (1) 渤海海域潮流以往复流和旋转流为主,其中渤海中北部以旋转流为主,呈顺时针旋转,涨落潮流向以NW-SE向为主.渤海海域潮流流速较小,且涨落潮流速相差小,变幅也小.其中,秦皇岛海域处于无潮点附近,潮流流速更小. (2) 对于密度大粘度高的蓬莱19-3溢油风拖拽系数合理范围为1.4~2.3%;扩散系数公式中校正参数b对溢油的扩散范围影响较大,其合理取值范围为0.38~0.42. (3) 渤海夏季风速较大、风向较为稳定的南风和东南风对漂浮于水面上的溢油作用较大,且溢油漂移方向与主风向大致相同.而渤海潮流以往复流和旋转流为主,溢油在涨落潮流的作用下会出现来回摆动,净位移小,潮流对溢油的漂移不及风的作用. (4) 溢油初期的蒸发速度较快;由于挥发组分的减少以及乳化作用使溢油含水率增大,溢油后期的蒸发速度明显减小.进入沿岸海域后溢油容易发生附岸,附岸和蒸发使得溢油漂浮组分逐渐减少.最终,漂浮组分、蒸发组分和附岸组分分别占溢油总量的30.6%、44.0%和24.9%,蒸发和附岸是溢油的主要归宿. [1] 张丽萍,王辉.不同海面状况海洋石油污染处理方法优化配置[J].海洋技术,2006,25(3):1. ZHANG Liping, WANG Hui. Optimization design of countermeasures to cleanup the marine oil pollution in different sea surface conditions.[J].Ocean Technology,2006,25(3):1. [2] 徐艳东.海上溢油风化过程及其预测模型研究[D].青岛:中国海洋大学,2006. XU Yandong. A study on theweathering and predicting model of spilled oils at sea[D]. Qingdao: Ocean University of China,2006. [3] DENG Zenggan, YU Ting, JIANG Xiaoyi,etal. Bohai Sea oil spill model: a numerical case study[J]. Marine Geophysical Research.2013,34(2):115. [4] 国家海洋局.蓬莱19-3油田溢油事故联合调查组关于事故调查处理报告[R].北京:国家海洋局,2011[2015-02-03]. http://www.soa.gov.cn/xw/hyyw_90/201211/t20121109_884.html. State Oceanic Administration People’s Republic of China. The joint investigation group report on the investigation and handling of the Penglai 19-3 oil spill accident[R].Beijing: State Oceanic Administration People’s Republic of China, 2011[2015-02-03]. http://www.soa.gov.cn/xw/hyyw_90/201211/t20121109_884.html. [5] KUANG Cuiping, PAN Yi, HU Ying,etal. Primary analysis of the 2011ConocoPhillips oil spill in Bohai Bay, China [C]// Advances in Biomedical Engineering——2012 Asia Pacific Conference on Environmental Science and Technology (APEST 2012). Kuala Lumpur: Information Engineering Research Institute,2012:1-5. [6] DENG Zenggan, YU Ting, SHI Suixiang,etal. Numerical study of the oil spill trajectory in Bohai Sea, China[J]. Marine Geodesy,2013,36(4): 351. [7] XU Qing, LI Xiaofeng, WEI Yongliang,etal. Satellite observations and modeling of oil spill trajectories in the Bohai Sea[J]. Marine Pollution Bulletin,2013,71(1/2):107. [8] WANG Shoudong, SHENYongming, ZHENG Y.H. Two-dimensional numerical simulation for transportand fate of oil spills in seas[J]. Ocean Engineering,2005,32(13):1556. [9] WANG Shoudong, SHEN Yongming, GUO Yakun,etal. Three-dimensional numerical simulation for transport of oil spills in seas[J]. Ocean Engineering,2008,35(5): 503. [10] WANG Jinhua, SHEN Yongming. Development of an integrated model system to simulate transport and fate of oil spills in seas[J].Sciences China-Technological Sciences,2010,53(9): 2423. [11] BI Haipu, SI Hu. Numerical simulation of oil spill for the Three Gorges Reservoir in China[J]. Water and Environment Journal,2014,28(2):183. [12] LI Yan, ZHU Jiang, WANG Hui. The impact of different vertical diffusion schemes in a three-dimensional oil spill model in the BohaiSea[J]. Advances in Atmospheric Sciences,2013, 30(6): 1569. [13] WL|DelftHydraulics. User manual Delft3D-FLOW[M].Delft: WL|Delft Hydraulics, 2013. [14] WL|DelftHydraulics. User manual D-WaqPART[M].Delft: WL|Delft Hydraulics, 2013. [15] Fingas M, Filedhouse B, Mullin J. Water-in-oil emulsions results of formation studies and applicability to oil spill modeling[J].Spill Science & Technology,1999,5(1): 81. [16] Mackay D, Paterson S, Trudel K. A mathematical model of oil spill behavior on water with natural and chemical dispersion. [R]. Ottawa: Environment Canada, 1977. [17] Fingas M F. Chemistry of oil and modelling of spills[J].Journal of Advances in Marine Technology Conference,1994, 11: 41. [18] Willmott C J. On the validation of models[J].Physical Geography,1981, 2(2):184. [19] 王广源,周心怀,王昕,等.蓬莱19-3/25-6油田未熟-低熟油特征与成因[J].石油实验地质, 2014,36(2):231. WANG Guangyuan, ZHOU Xinhuai, WANG Xin,etal. Characteristics and genesis of immature and low-matire oils in Penglai 19-3/25-6 oilfields[J]. Petroleum Geology & Experiment, 2014, 36(2):231. Numerical Simulation and Analysis of Transport and Fate of Penglai 19-3 Oil Spill KUANG Cuiping1, XIE Hualang1, SU Ping2, CHEN KUO1 (1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. Guangxi Communications Planning Surveying and Designing Institute, Nanning 530029, China) The numerical model of oil spill transport and fate in the Bohai Sea is set up by coupling with the hydrodynamic model. The change processes of spilled oil included in the model are drift, dispersion, evaporation, emulsification and so on. The drift process is simulated by the Lagrange method, while the turbulent dispersion process is considered by using the ‘Monte Carlo method’, turbulent dispersion of spilled oil changes over time by using the time-varying turbulent dispersion coefficient. The reasonable ranges of wind drag coefficient and the dispersion correction parameterbfor Penglai 19-3 oil spill model obtained by calibration are 1.4~2.3% and 0.38~0.42, respectively. Then, the Penglai 19-3 oil spill accident in the Bohai Sea is used to verify the oil spill model by comparing the time and location of spilled oil arrival at shore, and the simulation results are consistent with the actual situation. The numerical results show that the wind, because of its large velocity and small change in direction, plays a major role on the drift of spilled oil floating on the water surface, and the drift direction of spilled oil is roughly the same with the main direction of wind. The effect of the tidal current, which is dominated by reversing current and rotary current with a very weak residual current, to the drift of spilled oil in Bohai Sea is less than the effect of the wind. The evaporation rate of spilled oil is quite large in the initial stage after oil spill, but significantly reduced in the later stage as a result of the reduction of the volatile fraction and the increase of the water content caused by emulsification. The reduction of floating oil is mainly caused by evaporation and sticking that are also the main fates of spilled oil. Bohai Sea; oil spill; transport and dispersion; numerical simulation 2015-02-06 国家海洋公益项目(201305003) 匡翠萍(1966—),女,教授,博士生导师,工学博士,主要研究方向为河口海岸工程和环境.E-mail:cpkuang@tongji.edu.cn X55; P76 A
2 数学模型建立与验证


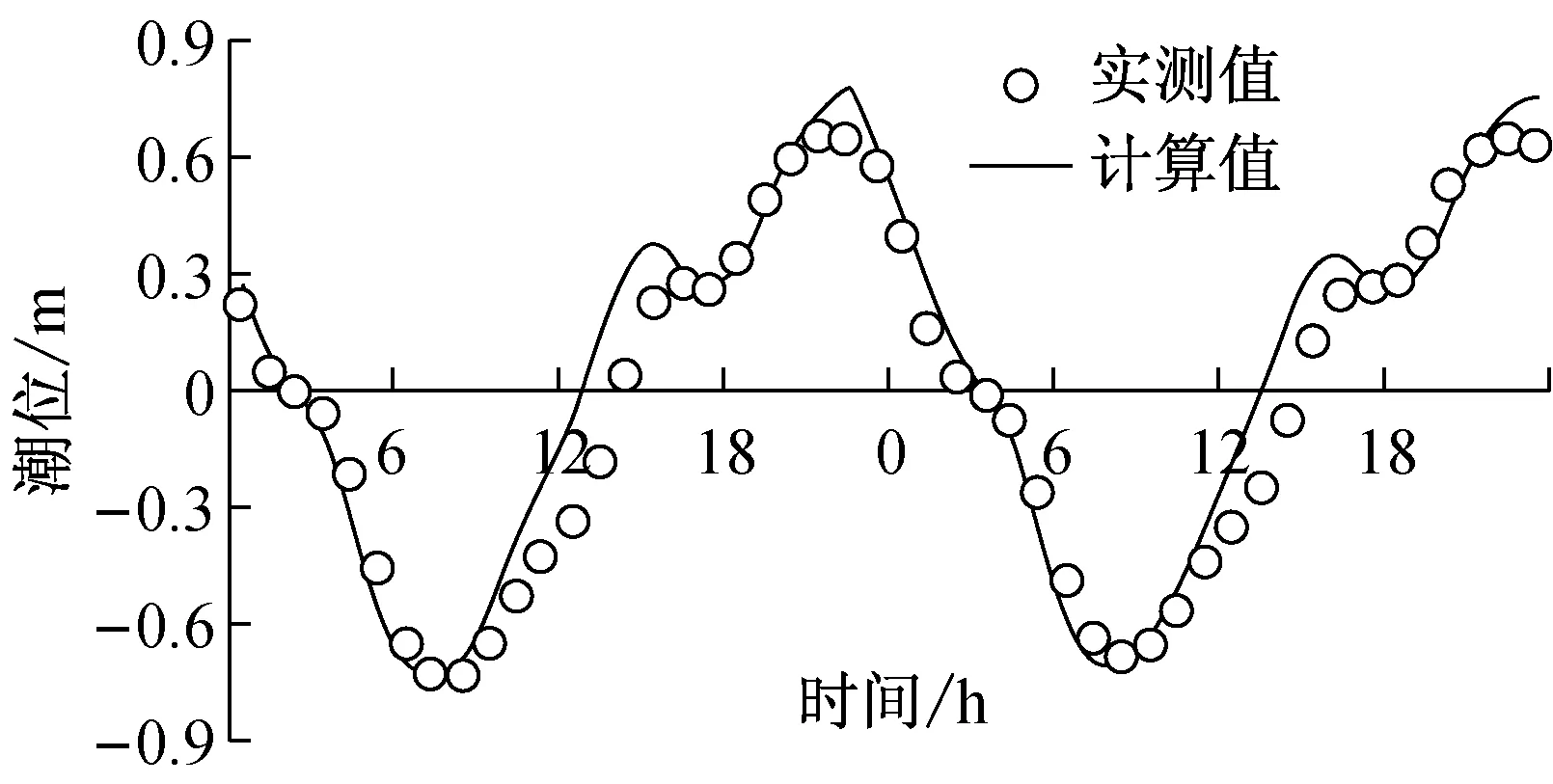



















3 模拟结果与分析








4 结论

