基于稀疏表示和近邻嵌入的图像超分辨率重构
常志国,郭茹侠,李 晶,胡云鹭
(长安大学 信息工程学院,西安 710064)
基于稀疏表示和近邻嵌入的图像超分辨率重构
常志国,郭茹侠,李晶,胡云鹭
(长安大学信息工程学院,西安710064)
提出基于稀疏表示和近邻嵌入的单帧图像超分辨率重构算法;为低分辨率和高分辨率图像块训练两个基于稀疏表示的过完备字典,在训练的低分辨率图像块和高分辨率图像块中分别选取与这两个字典原子最近的图像块近邻,通过图像块近邻来计算构图像块的权重;一旦得到权重矩阵,高分辨率重构图像块可以由低分辨率图像块与相应权重相乘来表示;与之前的算法相比,所提出的算法在计算字典原子与图像块距离的时候不是逐个图像块进行计算,而是先将图像块聚类,计算字典原子与类中心的距离,在距离最近的一类中选取图像块;计算权重矩阵的时间可以大大减少,提高计算效率;所得到的PSNR与其它算法相比,也有一定提高。
超分辨率重构;稀疏表示;过完备字典;图像块近邻;权重
0 引言
图像超分辨率放大能够将低分辨率图像放大又能够恢复图像的高频细节。当然图像超分辨率放大是一个病态问题,因为根据图像放大的倍数,会将一个低分辨率像素点映射成多个高分辨率像素点。
近邻嵌入的方法就是为了降低图像超分辨率重构的时间复杂度和存储需求。近邻嵌入假设低分辨率块和高分辨率块在低维空间具有相似的局部纹理,使用与低分辨率图像块相同的插值系数产生高分辨率输出块。NE+LLE[18]对于重构的低分辨率图像块,在训练的低分辨率图像块集合中寻找K个近邻,将K个近邻线性组合来表示重构的低分辨率图像块,得到这个线性组合系数即权重,最小化重构误差,最后使用相应的K个高分辨率图像块近邻和权重计算高分辨率输出图像块。权重的限制条件一般为近邻的权重之和为1,在NE+NNLS[19]中,为了降低算法复杂度,将权重的限制条件改为非负数,即权重大于零。近邻嵌入算法与稀疏表示相比可以明显降低算法的复杂度和内存需求,然而由于缺乏先验知识,重构的效果并不比稀疏表示的好。将稀疏表示模型与近邻嵌入模型结合起来,既能够降低算法复杂度图像的重构结果又较好。Timofte提出的ANR[20]结合了这两种算法。ANR[20]为每个输入块计算它在字典中的最近邻原子,只使用近邻的字典原子而不是整个字典,大大降低了计算复杂度和重构时间。为了建立图像块与字典之间的联系,Timofte提出了A+[21]算法,使用Zedey方法训练的字典,计算训练的图像块与字典原子之间的近邻,选择K个近邻高分辨率和低分辨率图像块计算映射的权重矩阵。建立在稀疏表示和近邻嵌入基础上的算法,能够减少计算复杂度,加强图像的表示能力。
本文中采用的算法也是由近邻嵌入和稀疏表示结合起来的。我们的算法中先分割图像块,使用Zedey训练字典的方法训练高分辨率和低分辨率字典,计算切割的图像块与字典原子之间的距离。这里与A+算法的不同之处在于图像块的选择。A+算法中逐个计算图像块与字典原子之间的距离,选择K个图像块近邻。然而由于图像块过多,在计算欧几里得距离时花费时间过长,而且很容易导致内存溢出。我们的算法先将图像块聚类,计算类中心与字典原子之间的距离,在与字典原子最近的类中选择K个图像块。与A+相比计算时间大大减少,而与ANR相比,图像的PSNR也有所提高。
1 稀疏表示模型
图像超分辨率型可以表示为y=βx,其中x表示高分辨率图像,y表示低分辨率图像,β表示对高分辨率图像x进行的模糊和下采样操作,通过这个操作使低分辨率和高分辨率图像保持一致。现在已知低分辨率图像y,为了得到高分辨率图像x,可以通过最小二乘法来求解此式
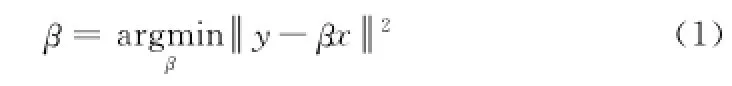
为了避免方程出现病态过拟合问题,加入正则项l1范数,可以得到(2)式
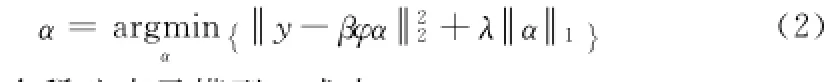
这是一个稀疏表示模型,式中
x=φα(3)
图像块可以表示为过完备字典和稀疏系数的线性组合[5],φ是具有K个原子的过完备字典,α是稀疏表示系数,其大部分元素为0。即在过完备字典中选择合适的原子可以对图像块进行稀疏表示。(2)式求解的方法。字典学习的方法也有很多种,如在线字典学习[25],K-SVD算法等。一旦得到一对过完备字典,将输入的低分辨率图像块表示为低分辨率字典和稀疏系数的乘积,则高分辨率图像块就可以通过高分辨率字典和稀疏表示系数重建。
2 图像块近邻嵌入模型
假设有一组高分辨率图像x1,x2,x3…xN,使用双三次插值下采样再上采样得到其相应的低分辨率图像y1,y2,y3…yN。将两组图像切割成小块,图像块大小为m×M。得到集合Ω={~xi,~yi},其中~xi,~yi分别表示切割的第i个高分辨率和低分辨率图像块,i=1…P,P为图像切割的总块数。将一个低分辨率输入图像块L表示为权重与图像块近邻的乘积,图像块的近邻是在集合Ω中选取的,通过计算输入的图像块与集合中的图像块之间的欧几里得距离来得到图像块的近邻。假设在集合中选取了图像块的K个近邻,则权重的计算方法可以由(4)式给出

j=1…K表示图像块的K个近邻。如果(~yjT~yj)-1存在,则方程的代数解为(5)式
ω=(~yjT~yj)-1~yjTL(5)
为了避免方程出现病态过拟合问题,给此权重加入正则项,可以得到(6)式

由(6)式可以得到权重的代数解(7)式
ω=(~yjT~yj+λΙ)-1~yjTL(7)
一旦得到权重系数矩阵,则高分辨率图像块可以通过(8)式重建
H=~xjω(8)
式中,H表示重建的高分辨率图像块,~xj表示集合Ω中相应于低分辨率图像块~yj的高分辨率图像块。
3 基于稀疏表示和图像块近邻的图像超分辨率重构
稀疏表示模型虽然能够很好地表示图像块,但是字典训练会花费很长时间,内存占用过大;近邻嵌入模型能够很好地解决图像超分辨率重构的时间复杂度和存储需求。将这两种方法结合起来。设第i高分辨率和相应的低分辨率图像块分别为~xi,~yi,则由公式(2)可以得到公式(9)

αi为低分辨率图像块的稀疏表示系数,使用OMP求解αi,固定αi,对低分辨率字典φy用K-SVD算法进行逐列更新。使用同样的方法可以得到高分辨率字典φx。
由公式(7)和公式(8)可以得到公式(10)
H=x~j(~yjTy~j+λΙ)-1~yjTL(10)
如果给输入的低分辨率图像块L乘以一个矩阵,就可以得到要重构的高分辨率图像块。这个矩阵是由图像块近邻构成的,将其称为映射矩阵,乘以这个矩阵就可以将低分辨率图像块映射为高分辨率图像块,即公式(11)
Pj=xj~(~yjTyj~+λΙ)-1yj~T(11)
由于映射矩阵Pj是在未知低分辨率图像块L的情况下事先计算好的,要得到低分辨率图像块的近邻y~j和相应的高分辨率近邻x~j就不能使用近邻嵌入的方法。Timofte在ANR[20]中结合了字典训练[12]的思想,为事先训练好的低分辨率字典φy和高分辨率字典φx中的每个原子计算K′个近邻,用字典原子近邻来代替图像块近邻,得到每个字典原子的映射矩阵Pl,l =1…K′表示计算的K′个近邻。最后通过为每个输入块计算它在字典中的最近邻原子,使用这个原子对应的映射矩阵将其映射到高分辨率空间。
为了加强图像块与映射函数之间的联系,Timofte在A+中同样使用了Zedey训练的高分辨率和低分辨率字典。计算图像块集合Ω={x~i,~yi}中,低分辨率图像块y~i与每个低分辨率字典原子之间的欧几里得距离,在低分辨率图像块中选择与字典原子最近的K个低分辨率图像块,和相应的高分辨率图像块,可以得到公式(11)中的映射函数。
由于要计算每个图像块与字典原子之间的距离,当图像块数量较大时,计算这个距离所花费的时间较长。本文中为了降低算法的运行时间同时保证重构图像块的PSNR不会骤降,事先将切割的高分辨率和相应的低分辨率图像块使用k—means进行聚类,聚类之后我们只计算聚类中心与字典原子之间的欧几里得距离,最后在距离字典原子最近的一类中选择K个低分辨率和相应的高分辨率图像块,这将会大大降低算法复杂度,减少运算时间。
4 算法流程
基于稀疏表示和图像块近邻的单帧图像超分辨率重构算法流程如图1所示。

图1 基于稀疏表示和图像块近邻的图像超分辨率重构算法流程图
算法步骤如下。
输入:高分辨率训练图像和低分辨率待重构图像;
输出:高分辨率重构图像。
1)将高分辨率训练图像双三次插值下采样再上采样得到其相应的低分辨率图像,
两组图像切割成m×M的小块,得到高分辨率和低分辨率图像块集合Ω={~xi,~yi}。
2)使用Zedey的算法分别对图像块训练高分辨率字典φx和低分辨率字典φy
3)将集合Ω中的高分辨率和低分辨率图像块分别聚类,聚类个数为~K。我们使用K-means聚类,首先初始化~K个聚类中心,计算图像块与聚类中心的距离,图像块聚类后,求得每类的均值,作为新的聚类中心,不断重复迭代,直到均方差收敛。
4)使用欧几里得距离公式计算每个聚类中心与低分辨率字典φy中的每列字典原子之间的距离。
5)将计算的距离按从小到大顺序排序,选择距离字典原子最近的一类C。
6)在最近的一类C中选取K个低分辨率近邻图像块和相应的高分辨率图像块。
7)使用公式(11)计算映射函数Pj。
8)将输入的低分辨率图像转化到YCbCr空间,对亮度图像进行双三次插值放大,
用f1=[-1,0,1],fT1=[-1,0,1]',f2=[1,0,-2,0,1],fT2=[1,0,-2,0,1]'特征算子与亮度图像卷积,得到一阶二阶水平和垂直梯度图,将梯度图切割成m×m的小块,重叠像素为ω。
9)为输入的图像块计算其在字典中的最近邻原子,找到此原子对应的映射矩阵,与图像块相乘得到重建的高分辨率图像块。
10)所有高分辨率图像块恢复后,使用重叠像素ω重建高分辨率图像。
5 实验结果分析
5.1参数设置
试验中我们将低分辨率图像放大3倍。基于人眼对亮度信息敏感这个条件,我们将待重构的图像转化到YCbCr空间,只对亮度通道进行超分辨率放大。为了能够更好地求得图像块与字典原子之间的最近邻,图像块要尽可能多地切割。对25幅图像进行大小为3×3的块切割,重叠像素为2。字典的大小设置为1 024,图像块聚类个数~K为50,选取K为1 024个与字典原子近邻的图像块。公式(11)中λ的值是为了平衡公式之间的关系,防止出现奇异值。这里λ的值与A+设置相同为0.1。
5.1.1图像块大小以及重叠像素的影响
对于近邻嵌入来说,图像块的大小有着很重要的影响。因为要在切割的图像块库中选择与字典原子的近邻图像块。如果图像块过大,则选择的图像块多样性会变少,不能保障选取的图像块就是距离原子最近的图像块,图像块切割过小重构会引入人工痕迹。实验中分别采用3×3,5×5,7×7的图像块,由图2可以看出,随着图像块的增大,重构图像的PSNR会减小。重叠像素越大,重构图像越平滑,图像PSNR越大。因此实验中选择大小为3×3,重叠像素为2的图像块。
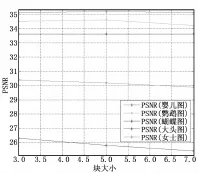
图2 不同图像块大小对图像PSNR的影响
5.1.2近邻数目K的影响
近邻个数的选取对实验结果也具有很大的影响。给字典原子在图像块中选择近邻,选择的近邻与字典原子越接近,近邻个数越多,图像的重构效果越好。图3分别是给字典选择1 024和2 048个图像块近邻,重构图像的PSNR。虽然字典原子的图像块近邻越多,重构效果越好,但是图4可以看出图像块越多,在计算映射函数时花费的时间也越长,为了平衡PSNR与时间复杂度之间的关系,我们在实验中选择1 024个图像块近邻。
5.1.3字典大小的影响
实验中将字典的大小分别设置为256,512,1024,以评估字典大小对实验数据的影响。由图5可以看出字典越大,重构图像的PSNR越好。这是因为字典原子越多,对图像的表示越准确,字典原子的关系与图像块的关系也越密切。然而随着字典原子的增大,所占的内存空间也会增加,影响计算时间。由于图像块聚类减少了计算时间,这里不将牺牲字典原子作为节省时间的代价,因此设置字典的大小为1 024。
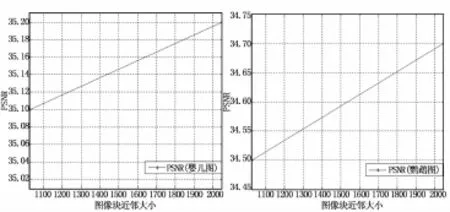
图3 图像块近邻大小对图像PSNR的影响
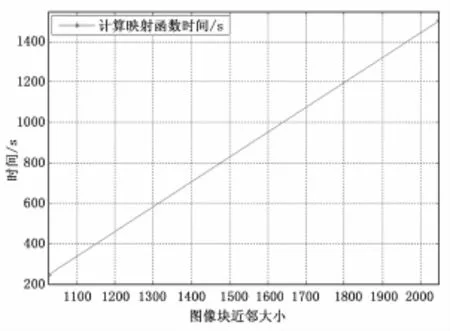
图4 图像块近邻大小对计算映射函数时间的影响
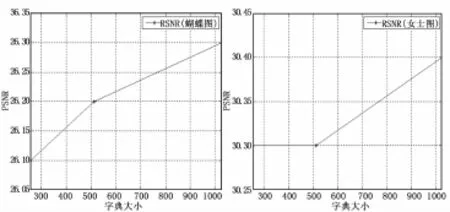
图5 字典大小对图像PSNR的影响
5.2实验结果对比
我们从客观和主观方面对图像的重构结果进行评估。客观方面通过峰值信噪比(PSNR)和时间复杂度对所提出的算法进行评估。PSNR越大,说明图像恢复的越好。主观方面可以从重构图像的纹理恢复程度,边缘恢复程度以及引入人工痕迹的程度进行评估。表1分别将所提出的算法与双三次插值,杨的算法,Zedey的算法,ANR算法,NE+LLE,NE+NNLS,A+算法作比较。从表1和图6,图7可以看出,近邻嵌入较稀疏表示而言,具有更好的重构效果;A+算法与其它算法比较具有更好的重构效果。我们的算法是在A+的基础上改进了计算映射函数的时间。从表1和表2(选择1024个图像块近邻,A+算法与我们算法在计算映射函数时间上的比较)看出,虽然和A+相比,PSNR并没有提升,但是在保证PSNR不会明显下降的情况下,减少了运行时间,这对于实际的工程应用来说是很重要的。从视觉角度来看,图像重构后的效果也比较好。

表1 三倍超分辨率放大结果比较
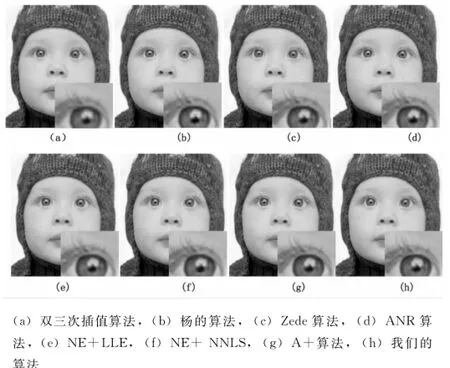
图6 婴儿图像放大三

图7 蝴蝶图像放大三

表2 计算映射函数所用时间
6 结论
本文提出基于稀疏表示和图像块近邻的单帧图像超分辨率重构算法,这个算法是在已有的算法基础上为了节省运行时间而提出来的。实验结果表明,所提出的算法在减少计算时间的情况下对图像的恢复程度也具有较好的效果。未来图像超分辨率放大技术不仅可以用于图片的超分辨率放大,也可以用于对视频图像的处理,然而如何降低学习的算法复杂度使其能够更好地适应环境变化以及实时处理图片和视频仍然是一个待解决的问题。
[1]Sun J,Xu Z,Shum H-Y.Image super-resolution using gradient profile prior[A].IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR)[C].Anchorage:IEEE,2008:1-8.
[2]D G,S B,Michal I.Super-resolution from a single image[A].The 12th International Conference on Computer Vision[C].Kyoto:IEEE,2009:349-356.
[3]Jianchao Y,John W,Thomas H,Yi M.Image super-resolution as sparse representation of raw image patches[A].IEEE Conference on Computer Vision and Pattern Recognition(CVPR)[C].Anchorage:IEEE,2008:1-8.
[4]Sun J,Zhu J,F TM.Context-constrained hallucination for image superresolution[A].IEEE Conference on Computer Vision and Pattern Recognition(CVPR)[C].San Francisco:IEEE,2010:231-238.
[5]Jianchao Y,John W,Thomas H,Yi M.Image Super-Resolution Via Sparse Representation[J].IEEE Transactions on Image Processing,2010,19(11):2861-2873.
[6]Jianchao Y,Zhaowen W,Zhe L,Xianbiao S,Thomas H.Bilevel sparse coding for coupled feature spaces[A].IEEE Conference on Computer Vision and Pattern Recognition(CVPR)[C].Providence:IEEE,2012:2360-2367.
[7]Jianchao Y,Zhaowen W,Zhe L,Scott C,Thomas H.Coupled Dictionary Training for Image Super-Resolution[J].IEEE Transactions on Image Processing,2012,21(8):3467-3478.
[8]Shenlong W,Lei Z,Yan L,Quan P.Semi-coupled dictionary learning with applications to image super-resolution and photo-sketch synthesis[A].IEEE Conference on Computer Vision and Pattern Recognition(CVPR)[C].Providence:IEEE,2012:2216-2223.
[9]Elad M,Aharon M.Image Denoising Via Sparse and Redundant Representations Over Learned Dictionaries[J].IEEE Transactions on Image Processing,2006,15(12):3736-3745.
[10]Weisheng D,Lei Z,Guangming S,Xin L.Nonlocally Centralized Sparse Representation for Image Restoration[J].IEEE Transactions on Image Processing,2013,22(4):1620-1630.
[11]Sulam J,Ophir B,Elad M.Image Denoising Through Multi-Scale Learnt Dictionaries[A].IEEE International Conference on Image Processing[C].Paris:IEEE,2014:808-812.
[12]Zeyde R,Elad M,Protter M.On Single Image Scale-Up Using Sparse Representations[C].Curves and Surfaces Avignon,2010:711-730.
[13]X J.Image Super-resolution by Mid-Frequency Sparse Representation and Total Variation Regularization[J].Journal of Electronic Imaging,2015,24(1):13-39.
[14]Pati Y C,Rezaiifar R,Krishnaprasad P S.Orthogonal matching pursuit:recursive function approximation with applications to wavelet decomposition[A].Conference Record of The Twenty-Seventh Asilomar Conference on Signals,Systems and Computers[C].Asilomar:IEEE,1993:40-44.
[15]Mallat S G,Zhang Z.Matching pursuits with time-frequency dictionaries[J].IEEE Transactions on Signal Processing,1993,41(12):3397 -3415.
[16]Aharon M,Elad M,Bruckstein A.K-SVD:An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation[J]. IEEE Transactions on Signal Processing,2006,54 (11):4311-4322.
[17]Rubinstein R,Zibulevsky M,Elad M.Efficient implementation of the K-SVD algorithm using batch orthogonal matching pursuit[R].2008.
[18]Hong C,Dit-Yan Y,Yimin X.Super-resolution through neighbor embedding[A].IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR)[C].New York:IEEE,2004:275-282.
[19]Bevilacqua M,Roumy A,Guillemot C,Alberi M.Low-Complexity Single-Image Super-Resolution based on Nonnegative Neighbor Embedding[A].The British Machine Vision Conference(BMVC)[C].Guildford 2012:1-10.
[20]Timofte R,De Smet V,Van Gool L.Anchored Neighborhood Regression for Fast Example-Based Super Resolution[A].International Conference on Computer Vision(ICCV)[C].Sydney:IEEE,2013:1920-1927.
[21]Timofte R,De Smet V,Van Gool L.A+:Adjusted Anchored Neighborhood Regression for Fast Super-Resolution[A].Asian Conference on Computer Vision(ACCV)[C].Singapore,2014:111-126.
[22]Daubechies I,Defrise M,Mol CD.An Iterative Thresholding Algorithm for Linear Inverse Problems with A Sparsity Constraint[J].Communications on Pure and Applied Mathematics,2004,57(11):1413-1457.
[23]LCombettes P,Wajs VR.Signal Recovery by Proximal Forwardbackward Splitting[J].Soc Ind Appl Math J Multiscale Model Simul,2005,4(5):1168-1200.
[24]Zibulevsky.M,Elad.M.L1-L2 Optimization in Signal and Image Processing[J].IEEE Signal Processing Magazine,2010,27(3):76-88.
[25]Julien Mairal,Francis Bach,Jean Ponce,Sapiro G.Online dictionary learning for sparse coding[A].Proceeding of the 26th International Conference on Machine Learning(ICML)[C].Montreal ACM,2009:689-696.
Image super-resolution Reconstruction Based on Sparse Representation and Neighbor embedding
Chang Zhiguo,Guo Ruxia,Li Jing,Hu Yunlu
(School of Information Engineering,Chang'an University,Xi'an710064,China)
A single frame image super-resolution reconstruction algorithm based on sparse representation and neighbor embedding was proposed.Two complete dictionaries based on sparse representation were trained for low and high resolution image patches,in which the closest image patches to the two dictionary atoms were chosen.The weight of reconstructed image patches was represented by image patches neighbor.Once weight matrix was gotten,High resolution image patch can be expressed as low resolution image patch multipling by the corresponding weight.Compared with previous algorithms,when calculating the distance between the dictionary atoms and image patches,the proposed algorithm is not each image patch to calculate.Instead image patches are clustered,and calculate the distance between dictionary atoms and the clustering center,then select image patches in the closest category.Calculated time of weight matrix can be greatly reduced,and improve the computational efficiency.The resulting PSNR compared with other algorithms,there are also improved obviously.
super-resolution reconstruction;sparse representation;complete dictionaries;neighbor embedding;weight
1671-4598(2016)05-0173-05
10.16526/j.cnki.11-4762/tp.2016.05.050
TP3
A
2015-10-21;
2015-12-08。
常志国(1976-),男,汉,山西,博士,副教授,主要从事视频图像处理方向的研究。

