基于节点吸引力的可调参数复杂网络模型

孙睿， 罗万伯

(1.成都师范学院 计算机科学系， 四川，成都 611130；2.成都大学 四川省模式识别与智能信息处理重点实验室，四川，成都 610106；3.四川大学 计算机学院， 四川，成都 610041)



基于节点吸引力的可调参数复杂网络模型

孙睿1，2， 罗万伯3

(1.成都师范学院 计算机科学系， 四川，成都 611130；2.成都大学 四川省模式识别与智能信息处理重点实验室，四川，成都 610106；3.四川大学 计算机学院， 四川，成都 610041)

针对真实网络的生长演化规律，以及BA无标度网络模型和原始的节点吸引力模型在择优连接以及生成网络统计特征方面所存在的问题，综合考虑复杂网络生长演化过程中节点度和节点吸引力的择优连接特性，提出了一种基于节点吸引力的可调参数复杂网络模型. 理论研究与仿真实验分析表明，基于节点吸引力的可调参数复杂网络模型可以有效生成结构稳定并与实际网络统计特征很接近的复杂网络，通过调节模型参数可以灵活调整网络的生长演化过程. 模型生成的网络度分布仍然服从幂律分布，并且具有较高的群集系数和平均路径长度.

复杂网络；节点吸引力；可调参数；节点度分布

现实世界中的诸多复杂系统都以网络的形式存在[1]，比如社会系统中的人际关系网、科学家合作网、世界贸易网和流行病传播网；生态系统中的食物链网、神经元网、新陈代谢网和蛋白质相互作用网；信息系统中的论文引用网、因特网和万维网；人工技术系统中的电话网、电力网和交通运输网等. 经过对真实网络的大量研究，Watts和 Stregatz以及Barabasi和Albert提出了WS小世界(small world) 网络模型[2]和BA无标度(scale free)网络模型[3]. 小世界效应、无标度特性以及社区结构(community structure)[4]等重要的拓扑结构属性的发现与研究，使得复杂网络的研究跨越了从20世纪60年代开始的以随机图理论[5]为主导的研究而进入了一个崭新的纪元，各种宏观性质的微观生成机制以及网络的演化规律等一系列问题的研究成为科研学者广泛关注的热点. WS模型和BA模型都具有非常简明的生成规则，但是同时也不可避免忽略了影响实际网络生长的因素，使得某些统计性质与实际网络相比有较大的偏差[6]. 比如WS小世界网络模型虽然具有现实网络的高聚类特征，但是其网络度分布近似于泊松分布；BA无标度网络模型的度分布服从幂律分布，这与现实网络是一致的，但其聚类效应却并不明显并且幂指数固定为常数3，这与实际网络幂指数通常在[1，3]的范围内不符.

近年来，为了克服上述的这些问题，学术界提出了许多相应的改进模型. Dorogovtsev[7]最早提出了原始节点吸引力模型(简称为Dorogovtsev模型)，Dorogovtsev模型规定网络中所有节点的初始吸引力都相等，网络的生长演化受节点吸引力的影响，此模型较好的解决了现实网络中孤立节点也会被连线的问题. 陶少华等[8]提出了一种基于节点吸引力的复杂网络模型(简称为NAM模型)，该模型以网络中的节点在单位时间内所获得的连接数作为节点的吸引力，同时假设各节点有同等的连接机会，模型的择优连接概率由节点吸引力和节点度共同决定. 田生文等[9]针对原始节点吸引力模型及其扩展模型普遍具有较小的群集系数这一缺陷，提出了一个具有聚类效应的节点吸引力复杂网络模型(简称为CALW模型). CALW模型分析了真实网络中择优连接的局域性特点，将节点的吸引力定义为随时间变化的函数，实验结果表明此模型具有较高的群集系数，更吻合实际网络的拓扑结构和统计特性. 本文在以上研究的基础上提出了一种基于节点吸引力的可调参数的复杂网络模型.

1 可调参数的节点吸引力模型

1.1 节点吸引力

许多真实网络都展现了择优连接的特征，这说明节点的连接概率与节点度是有关的，但是节点择优的选择标准并非都简单如BA模型所描述的只是选择节点度大的节点. 例如，在社交网络中每个人结交新朋友的速率并不完全相同，有些魅力十足的人会更容易的交友，而这样的人有时往往并不是在网络中非常活跃并广泛交流的人；在科研合作网络中，一个新加入的人员选择合作的对象既要是在网络中已经有很高的成就和威望的学者，又要是在与新加入者感兴趣领域近期比较活跃而有较多贡献的人员；在舆情网络中，一个节点如果是一个舆论观点的发起者或者是一个鲜明观点的支持者，那么它可能在短期内以更高的速率获得其他人的关注与联系. 以上的例子都说明在复杂网络的增长演化过程中，新节点的择优连接是普遍存在的，但选择的标准除了考虑节点的度还要考虑其他吸引因素.

定义吸引因子β，用来具体量化网络中节点对新节点的吸引力的大小，则每个节点的吸引因子表示为βi. 吸引因子βi的计算公式为

(1)

表示单位时间内节点获得连接数量的多少，其中ΔT=t-ti，ti表示节点vi在ti时刻加入网络，ni为节点vi在ΔT时间内获得的连接数量.

节点的度表示的是节点在网络中的拓扑位置，是某一时刻静态的度量，节点吸引力描述的是节点在一段时间内的连接变化，是一个对于动态过程的度量.

1.2 算法描述

对于真实复杂网络的大量实证研究表明，择优连接机制是具有普适性的复杂网络生长演化特性. BA模型是最具代表性的网络择优连接的生长模型，但是BA模型只考虑了节点度的择优连接，而完全忽略了节点吸引力的连接因素. Dorogovtsev模型则正好相反，它只依照节点吸引力的大小择优连接网络节点，而不考虑节点度的大小. CALW模型虽然具有聚类的特点，使生成的复杂网络具有与实际网络相似的较高的群集系数，但是CALW模型同样仅仅只以节点吸引力作为择优连接的标准. NAM模型虽然同时考虑了节点度和节点吸引力的择优连接，但是此模型中节点的连接概率只是这两者的简单线性相加，明显缺乏灵活性，这也极大地限制了模型的适用范围. 因此，针对以上的分析，本文在同时考虑节点度和节点吸引力这两个重要的择优连接因素的基础上，进一步设置了两个可调参数，用于根据复杂网络生长的真实环境来调节节点度和节点吸引力这两者在节点连接概率中所占的比重. 比如，因特网的网络生成过程往往更看重节点的度的大小，也就是新节点在加入网络时更偏重连接具有“明星效应”的节点，此时就可以相应增大模型中节点度的比例系数而生成更接近于真实的因特网拓扑属性的复杂网络；同理，在社交网络中，人们则更偏向于与对自己有足够吸引力的节点相连接，那么此时也可以减小节点度的参数值而增大节点吸引力的参数值，以此择优连接概率生成的网络就会更符合社交网络的真实情况.

可调参数的节点吸引力复杂网络模型的具体算法描述如下.

初始条件：初始时，网络是由m0个节点和e0条边组成的无向无权网络.

增长机制：在每个时间步，一个新节点vj加入到网络中，这个节点与网络中已经存在的m(m≤m0)个节点相连接.

择优连接：每个新节点vj与网络中旧节点vi相连的概率服从如下的规则

(2)

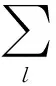
(3)

1.3 节点吸引力模型的度分布

假设新加入节点vj与原有节点vi相连接，则节点vi将会依照式(2)成比例的增加其度数ki，根据平均场理论[10]，则有

(4)

∂ki∂t=mαki+γβi∑l(αkl+γβl)=mαki+γβi2αmt+γ∑lβl.(5)

其初始条件是节点vi在ti时刻进入网络，其度数ki(ti)=m. 故方程(5)满足初始条件的解为

(6)

在ki≥0的部分，可将ki(t)的概率表示为

(7)

因为时间t是服从均匀分布的，所以

(8)

代入式(7)可得

(9)

因此，节点的度分布为

(10)

当t→+∞时，

(11)

所以，当α=1，γ=0时，模型退化为BA模型，P(k)≈2m2k-3；当α=γ=1/2时，P(k)≈2(m+βi)2(k+βi)-3，这与文献[8]所描述的情况相同，模型即为NAM模型；当α=0，γ=1时，网络择优连接完全按照节点吸引力的变化而变化，此时类似于文献[9]的模型中初始节点吸引力都相同的情况，模型退化为Dorogovtsev模型. 因此，本文提出的基于节点吸引力的可调参数复杂网络模型是一个综合了节点度择优连接以及节点吸引力连接的复杂网络生长演化的统一模型.

2 仿真实验与分析

根据本文提出的基于节点吸引力的可调参数复杂网络模型，利用计算机仿真实验，分别从度分布、群集系数、平均路径长度等复杂网络的特征参数与BA模型、NAM模型以及Dorogovtsev模型进行比较.

2.1 度分布

节点度是指网络中节点与其他节点间的连边数. 度分布则是节点恰好有k条连边的概率，用节点度的概率分布函数P(k)表示. 对真实复杂网络的实证研究表明，大多数复杂网络中节点度分布服从幂律分布，即P(k)～k-γ，其中2<γ≤3.

图1给出了几种模型的节点度分布情况，其中，网络模型参数为节点总数N=3 000，初始节点数m0=5，每个新节点的连接数m=3，可调参数α=1，γ=0；α=γ=1/2；α=0，γ=1；α=1/4，γ=3/4以及α=3/4，γ=1/4. 从图1可以看出，可调参数的节点吸引力模型与其他模型一样，其节点度分布服从幂律分布. 由此可见，虽然可以灵活调整模型的参数值，使其生成机制发生了相应的变化，但是网络的最终整体拓扑结构并没有发生太大的变化. 这表明同时考虑节点度与节点吸引力的择优连接机制是可以有效的生成结构稳定并与现实情况更接近的复杂网络的.

2.2 群集系数

图2是网络规模N取不同值时，几种模型群集系数C的比较. 从图2可以看出，本文提出的模型与其他模型生成网络的群集系数在变化趋势上基本一致，即随着网络规模的增大，群集系数降低；在同等的网络规模下，几种模型的群集系数差别不大，但是通过调整模型参数可以在一定程度上改变生成网络的群集系数. 当网络规模N=3 000时，群集系数C大致在0.012～0.017的范围内，基本与同等规模的实际复杂网络相吻合.

2.3 平均路径长度

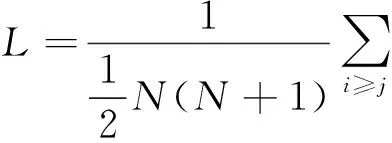
图3是网络规模N取不同值时，几种模型平均路径长度L的比较. 从图3发现几种模型的平均路径长度的增加速率大致相同，均与网络规模的对数成正比关系，这与现实世界中大多数复杂网络的特性相符合. 在同等的网络规模下，本文模型与BA模型、NAM模型的平均路径长度很接近，改变模型参数取值可以适当改变其平均路径长度，但是Dorogovtsev模型生成网络的平均路径长度明显要大于其他模型，这主要是因为Dorogovtsev模型在网络增长时只考虑节点吸引力因素而忽视了节点度的大小，模型更不易于聚集. 当网络规模N=3 000时，本文模型的平均路径长度L≈3.8，与同等规模的实际复杂网络大致相同.

3 结 论

研究了真实网络的生长演化规律，针对BA模型和原始的节点吸引力模型所存在的问题，提出了一种基于节点吸引力的可调参数复杂网络模型. 该模型考虑了网络演化过程中节点度与节点吸引力变化对于择优连接机制的影响. 理论研究与仿真实验分析表明，通过调节模型参数可以灵活调整网络的生长演化过程，使之更加符合真实网络的拓扑结构和统计特性.

[1] Sole R V. Complex networks: structure， robustness and function[M]. Cambridge: Cambridge University Press， 2012.

[2] Watts D J， Strogatz S H. Collective dynamics of small world networks[J]. Nature， 1998，393(4):440-442.

[3] Barabasi A L， Albert R. Emergence of scaling in random networks[J]. Science， 1999，286(5439):509-512.

[4] Nadakuditi R R， Newman M E J. Graph spectra and the detectability of community structure in networks[J]. Physical Review Letters， 2012，108(18):188701.

[5] Karrer B， Newman M E J. Random graphs containing arbitrary distributions of subgraphs[J]. Physical Review E， 2010，82(6):066118.

[6] Li M， Gao L， Fan Y， et al. Emergence of global preferential attachment from local interaction[J]. New Journal of Physics， 2010，12(4):043029.

[7] Dorogovtsev S N， Mendes J F F， Samukhin A N. Structure of Growing Networks with Preferential Linking[J]. Physical Review Letters， 2000，85(21):4633-4636.

[8] 陶少华，杨春，李慧娜，等.基于节点吸引力的复杂网络演化模型研究[J].计算机工程，2009，35(1):111-113.

Tao Shaohua， Yang Chun， Li Huina， et al. Research on complex networks evolution model based on node attraction[J]. Computer Engineering， 2009，35(1):111-113. (in Chinese)

[9] 田生文，杨洪勇，李阿丽，等.基于聚类效应节点吸引力的复杂网络模型[J].计算机工程，2010，36(10):58-60.

Tian Shengwen， Yang Hongyong， Li Ali， et al. Complex network model based on node attraction with clustering effect[J]. Computer Engineering， 2010，36(10):58-60. (in Chinese)

[10] Buice M A， Chow C C. Beyond mean field theory: statistical field theory for neural networks[J]. Journal of Statistical Mechanics: Theory and Experiment， 2013(3):P03003.

(责任编辑：刘芳)

Complex Network Model Based on Node Attraction with Tunable Parameters

SUN Rui1，2， LUO Wan-bo3

(1.Department of Computer Science， Chengdu Normal University， Chengdu, Sichuan 611130， China;2.Key Laboratory of Pattern Recognition and Intelligent Information Processing， Institutions of Higher Education of Sichuan Province， Chengdu University， Chengdu, Sichuan 610106， China;3.School of Computer Science， Sichuan University， Chengdu, Sichuan 610041， China)

According to the evolution rule of real-world networks and aiming at the problems existing in preferential attachment and statistical characteristics of network in BA model and initial attractive model, taking into account preferential attachment of node degree and node attraction in the evolution process of complex network, a complex network model based on node attraction with tunable parameters was proposed. Theory research and simulation analysis show the fact that the complex network model based on node attraction with tunable parameters can effectively generate networks with stable structure and actual statistical characteristics. Specifically, the degree distribution of networks still follows power-law distribution, while clustering coefficient and average path length are high.

complex network; node attraction; tunable parameters; degree distribution

2013-07-31

四川省教育厅自然科学重点资助项目(15ZA0330)；四川省教育厅创新团队资助项目(15TD0038)；成都师范学院培育资助项目(CS14ZD03)；成都师范学院高层次引进人才专项科研资助项目(YJRC2015-7)；成都大学模式识别与智能信息处理四川省高校重点实验室开放资助课题

孙睿(1982—)，男，博士，讲师，E-mail:cug123456@126.com.

TP 311； N 94

A

1001-0645(2016)01-0059-05

10.15918/j.tbit1001-0645.2016.01.011