云南省昭通市多尺度极端降水时空特征分析

李绅东

(云南省水文水资源局 昭通分局，云南 昭通 657000)



云南省昭通市多尺度极端降水时空特征分析

李绅东

(云南省水文水资源局 昭通分局，云南 昭通 657000)

为分析云南省昭通市多尺度极端降水时空特征，收集整理昭通市19个雨量站1969—2014年分时段逐年降水数据，并计算不同时间尺度(1，6，24 h)的年极端最大降水量，采用反距离加权法(IDW)插值展示其空间分布特性。在此基础上，对3个典型雨量站(鱼洞、新华、牛街)的极端最大降水进行深入分析，采用Mann-Kendall趋势检验及小波变换方法的趋势与周期分析，量化极端降水事件的时间分布特征。结果表明：昭通地区极端降水事件的空间分布规律为从北向南逐渐减少，且南北极端降水量相差较大，空间分布差异明显；3个典型雨量站多尺度极端降水变化趋势不显著(p>0.05)，其序列变化存在30，15，5～7 a 3个明显变化周期。

极端降水；时空特征；Mann-Kendall趋势检验；小波变换；昭通市

1 研究背景

近年来，受全球气候变化的影响，极端气候事件频繁发生[1-2]。暴雨，即极端降水事件，是极端气候事件的一种，且在近些年来发生频率更高、发生范围更广、影响范围更大，易造成山洪、泥石流、城市内涝等多种灾害，给人民生产、生活造成了严重影响[3-4]。昭通市位于云南省东北部，地处山区，气候、地形条件复杂多变，暴雨洪水灾害是昭通频繁发生、造成损失最惨重的自然灾害，严重制约了该市经济的发展和农村脱贫致富的进展。从20世纪80年代以来，昭通市发生洪灾频率有加大的趋势，给该市的防灾减灾工作带来了极大的难度[5]。因此，探讨昭通市极端降水的时空分布特征对部署防洪减灾工作及水资源充分利用具有十分重要的意义。

许多学者对昭通地区的暴雨特征进行了分析。宋昭义等[6]对昭通市昭阳区“7·14”特大暴雨进行了详细分析，并从地形、环流、河道形态等方面进行了成因分析，提出了有关防灾建议；罗奕群[7]从地形及天气系统两方面详细分析了昭通市的暴雨特性；姜云君等[8]利用常规气象观测资料，对2012年9月11日出现在滇东北的区域性暴雨天气过程进行诊断分析。在研究内容上，以上研究主要针对典型场次暴雨进行分析，并从地形、气候等方面研究暴雨成因，鲜有利用历年长序列降水实测数据分析地区极端降水的分布规律。在研究方法上，以上研究主要采用基本统计方法对暴雨特征进行简要分析，鲜有利用时间序列分析方法对降水数据的周期、趋势等规律进行分析，从而忽略了降水数据本身可能蕴含的潜在信息。同时，对昭通市极端降水空间分布特征的探索相对较少。

因此，在其他学者研究的基础上，本文重点关注昭通市极端降水的发生及分布规律，并侧重于对雨量站实测降水数据的挖掘。利用昭通市境内19个雨量站1969—2014年实测降水数据进行极端降水的时空分布特征分析，并选取昭阳区鱼洞站、绥江县新华站、彝良县牛街站3个代表雨量站时段(1，6，24 h)最大降水实测数据，采用Mann-Kendall趋势检验及小波变换等时间序列分析方法，分析降水序列周期与趋势变化规律，随后采用反距离加权插值方法进行极端降水特征空间分布规律分析，以期为昭通地区暴雨灾害风险规避提供科学依据。

2 研究方法

2.1 Mann-Kendall趋势检验

Mann-Kendall趋势检验方法(简称MK趋势检验)是非参数检验方法的一种，该方法不需要时间序列样本遵从某种特定的分布且其计算过程简便，故在水文领域内应用很广[9-10]。该检验方法的具体计算过程[11]如下。

对原始时间序列(x1,x2, … ,xn)，统计检验量S按式(1)计算。

(1)

式中Sgn为符号函数，根据式(2)计算。

(2)

统计检验量S服从正态分布，根据Var(S)=n(n-1)(2n+5)/18计算统计检验量S的方差。

若n>10，则标准的正态系统变量通过式(3)计算。

(3)

2.2 小波变换

有研究表明，Mexhat小波函数因其能满足容许性条件，因此能够更加精确地展现暴雨过程周期的时序性质[12-13]。鉴于该优点，本文研究中采用该小波函数对降水时间序列的变化进行研究，其函数表达式为

(4)

则降水时间序列f(t)∈L2(R)的离散Mexhat小波变换为[14]

(5)

式中：Wf(a,b)为小波变换系数；a为尺寸因子，反映周期长度；b为时间因子，反映时间上的平移。以b为横坐标、a为纵坐标可绘制关于小波变换系数的二维等值线图，该等值线图称为小波变换系数时频图。该图中等值线聚集的极大值点所对应的时间尺度即为该时间序列的周期。

将小波变换系数的平方值在b域上积分，可以得到小波方差，即[15]

(6)

小波方差随尺度a的变化过程，称为小波方差图，它能反映信号波动的能量随尺度a的分布，极大值处对应时间序列的周期，小波方差越大，该周期的强度越大。因此，可将小波方差图与小波系数时频分布图对比，验证小波变换分析的准确性。

2.3 反距离加权插值法

为分析昭通地区降水序列的空间分布特征，需采用空间插值方法将点降水数据插值到面上。在空间插值中，采用较多的是反距离加权插值法(Inverse Distance Weighted，IDW)、克里金插值法及样条插值法等。彭晓芬等[16]对云南省年均降雨量空间插值的研究中认为反距离加权插值法精度最高，而虎雄岗等[17]对云南省降雨量空间插值研究结果表明普通克里金与协克里金方法的插值精度较高。由于观测数据疏密程度对各种插值方法的结果影响较大，故不同学者采用不同站点数据可能得出不同的插值结果。因此，本文选取IDW方法进行空间插值，该方法原理简单(“相近相似”)、公式简便，在ArcGIS软件中操作方便，并被其他学者研究证明该方法能够描述云南地区降水的空间分布形态。

IDW插值公式[18]为

(7)

式中：Z为待插值点的估计值；Zi为第i个样本点的实测值；Di为第i个样本点与待插值点之间的距离；n为样本总数；p为距离的幂。p的大小会直接影响插值的效果，且p越大，插值结果越平滑。参考其他学者的研究，将IDW方法在云南降水插值进行应用，本文研究中p取值为2。

3 昭通市极端降水时空分布特征

3.1 研究区概况

昭通市位于云南省东北部，地处云、贵、川3省接合部，南北长234 km，东西宽241 km，周边长1 482 km，国土面积23 021 km2[19]。昭通市地理位置及县界区划如图1所示，其境内水系均属于长江水系，全市不同水系的径流面积总计约22 400 km2。本文在分析降水序列的时间变化特征时，根据现有观测资料中各站点所处的地理位置和观测雨量数据的完整性，选取昭阳区鱼洞站、绥江县新华站、彝良县牛街站3个代表性雨量观测站的降水数据进行MK检验以及小波变换的分析。

图1 研究区概况Fig.1 Overview of the study area

从图1可以看出，3个代表站点的地理位置分别位于昭通市的北、西南及东部，该三角形分布能够在一定程度上较全面反映全市极端降水序列的时间特性。本文在分析降水空间变化特征时，采用图1中所示全部19个站点1969—2014年实测极端降水量的均值进行反距离加权插值，进而得到降水的空间分布图并分析其特征。

3.2 极端降水时间分布特征

3.2.1 MK检验分析

根据3个代表雨量站1，6，24 h 3个时段的最大降水量统计，采用MK趋势检验方法分析3个代表站点的极端降水数据长期变化趋势，统计检验量如表1所示。

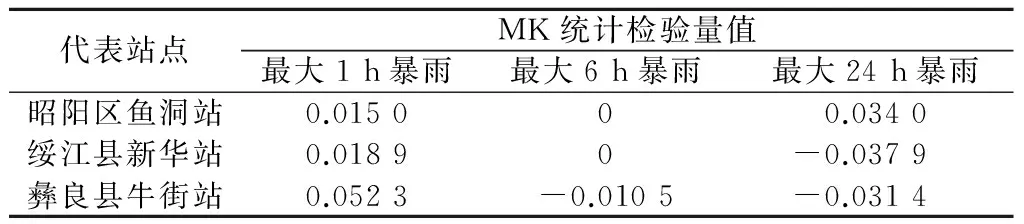
表1 代表站点MK趋势检验结果

通过MK检验可知，3个代表站点不同时段最大降水的趋势检验结果都处于0附近，说明各站点降水序列变化趋势不明显。其中，最大1 h降水量呈现上升趋势，最大6 h降水量无明显变化趋势。除鱼洞站最大24 h降水量呈现上升趋势，其他2站最大24 h降水量均呈现下降趋势。图2为3个雨量站3个时段内最大降水量的多年过程图。从图2中可以看出，随着时间的变化，各个站点的降雨序列的变化较为稳定。

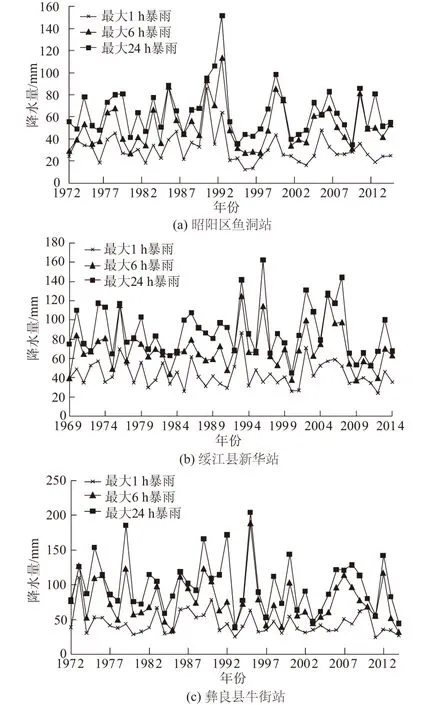
图2 昭通市3个站点暴雨量多年过程曲线Fig.2 Time-history curves of rainstorm for three typical stations in Zhaotong

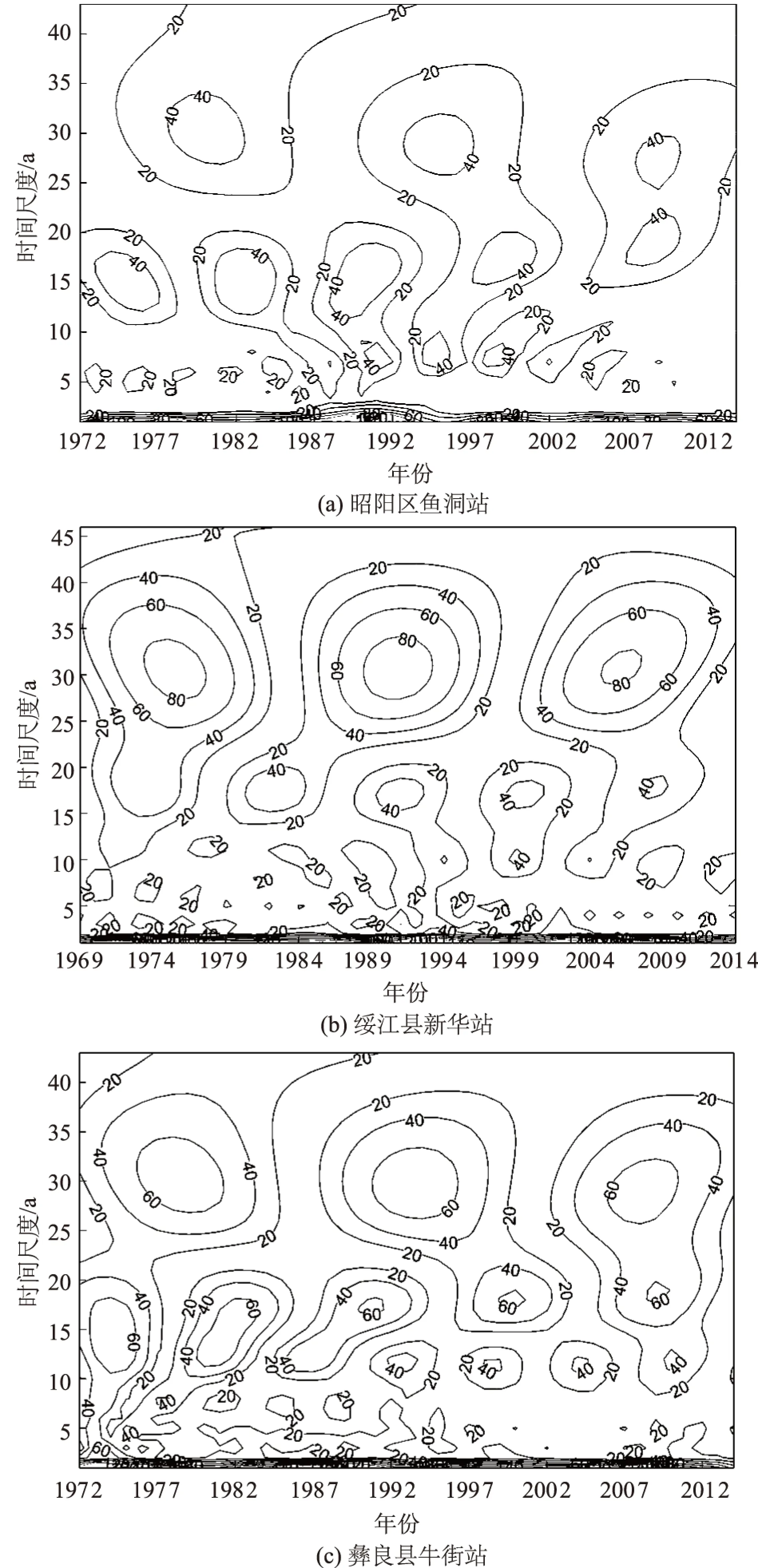
图3 昭通市3个站点小波系数时频分布Fig.3 Temporal frequencies of wavelet coefficients for three typical stations in Zhaotong

3.2.2 小波变换分析

运用小波变换方法对3个代表雨量站的1 h最大降水量进行周期特征分析。图3，图4分别为3个站点的小波系数时频图和小波方差图，结合图3和图4能够分析降水序列的周期变化规律。

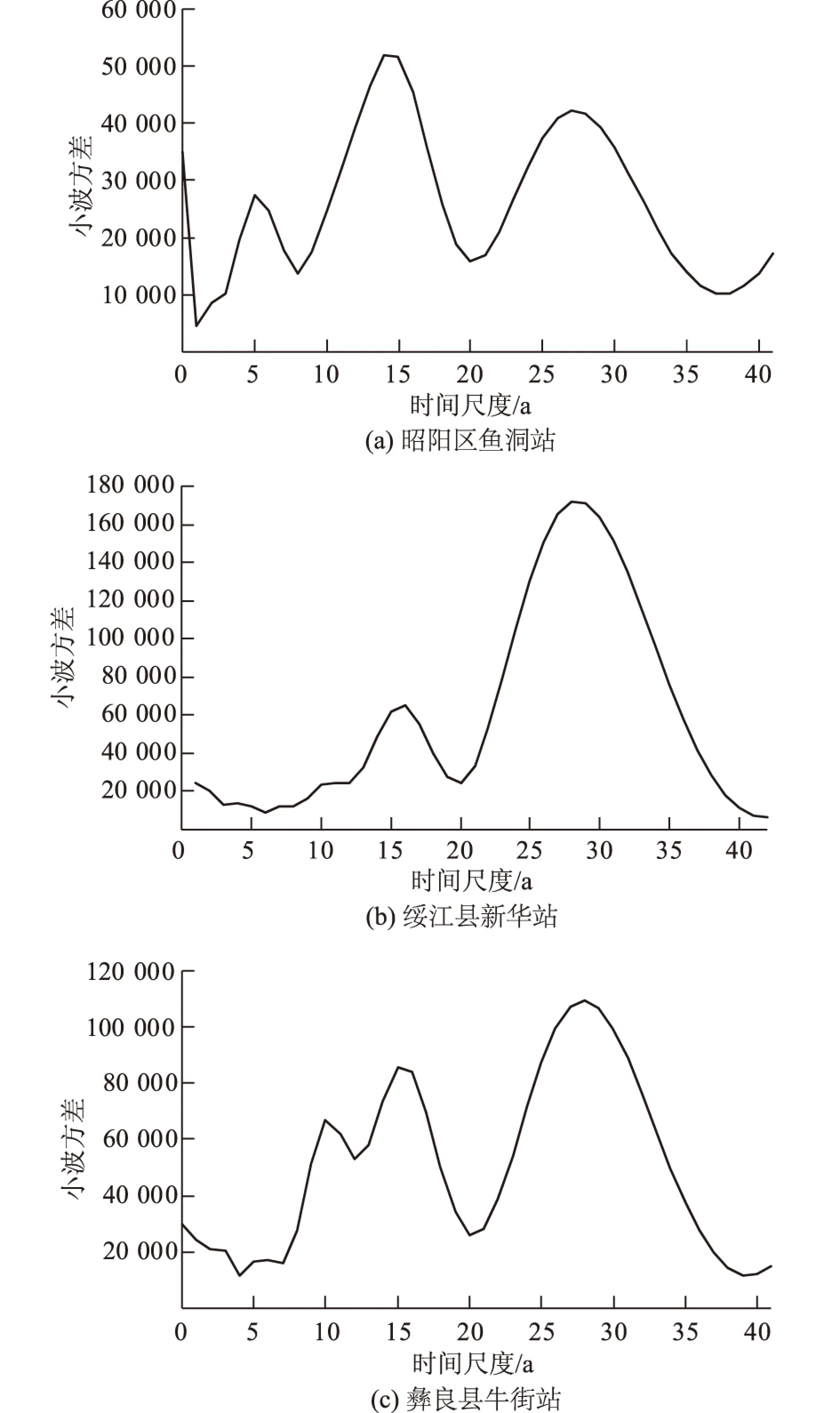
图4 昭通市3个站点小波方差Fig.4 Wavelet variances for three typical stations in Zhaotong

从图3中可以看出，鱼洞站降水序列存在约为30，15，5 a的变化周期；新华站存在约为30，17，7 a的变化周期；牛街站存在约为30，15，7 a的变化周期。从图4可以看出，鱼洞站降水序列的小波方差在5，15，30 a存在极值；新华站降水序列的小波方差在15，30 a存在极值；牛街站降水序列小波方差在10，15，30 a存在极值。由此可以看出，3个站点降水序列的小波系数时频分布图与小波方差图所反映的周期大致相同，说明小波变换方法能够有效分析序列的周期特征。对于整个昭通市来说其降水变化序列的周期约为30，15～17，5～7 a。

从上述3个站点的小波变换时频图及小波方差图的对比中可以看出，新华站和牛街站在30 a左右的变化周期非常明显，而鱼洞站的大尺度周期特征不如新华、牛街站显著。总体而言，新华站与牛街站的周期变化规律更为相似。

3.3 空间分布

根据昭通地区19个雨量站1969—2014年1，6，24 h的最大降水实测数据，对各站点历年实测数据求均值，并采用反距离加权插值法将点数据插值到空间，得到昭通市最大1 h、最大6 h、最大24 h降水空间分布，如图5所示。

从图5可以看出，昭通市1 h最大降水量的范围为30～50 mm，6 h最大降水量的范围为50～80 mm，24 h最大降水量的范围为60～110 mm；1，6，24 h最大降水量的空间分布特征相似，即从昭通市的东北部向西南部呈现依次减少的规律。其中，极端降水量最大的区域位于以彝良县牛街雨量站为中心的区域，极端降水量最小的区域为巧家县的南部地区。南北极端降水量差异较大，1 h最大降水量南北差异达到20 mm，6 h最大降水量南北差异达到30 mm，而24 h最大降水量南北差异高达50 mm之多。

图5 昭通市极端降水空间分布Fig.5 Spatial distribution of extreme precipitation in Zhaotong

结果显示的降水量呈现北多南少的主要原因为：昭通市处于云贵高原向川南丘陵的过渡带，山地高差悬殊，台阶地形迭置，垂直气候带显著，立体气候明显。由于“一带三台”及朝向北方的弧形地势及气流被北部坡面的抬升、阻挡、辐合及越过坡顶后的下沉、扩散影响，极端降水的分布也呈现自北向南逐渐减少的分布状况。

结合MK趋势检验及小波变换分析的结果，新华站与牛街站的周期变化特征更为相似，而鱼洞站与它们存在一定的差异；变化趋势上，同样是新华站与牛街站趋势相同，而鱼洞站存在一定差异。这可能是由于新华站与牛街站的空间位置处于相同的雨量带上，其空间属性相似，故时间变化规律相似。而鱼洞站所处的雨量带极端降水值偏小，故其周期特征差异较大。

4 结 论

本文利用昭通市境内19个雨量站1969—2014年降水实测数据进行极端降水的时空变化特征分析，着重选取昭阳区鱼洞站、绥江县新华站、彝良县牛街站3个代表雨量站1，6，24 h最大降水数据进行分析，分别采用Mann-Kendall趋势检验及小波变换方法，分析降水序列时间变化周期与趋势，最后采用反距离加权插值法进行极端降水空间特征分析，结果表明：

(1) 各代表站点降水序列变化较为平缓，趋势特征不明显。

(2) 3个代表性站点的最大1 h降水序列均存在约为30，15～17，5～7 a的3个变化周期。

(3) 昭通市极端降水在空间上呈现出由东北向西南依次减少的分布规律，且南北极端降水量相差较大，空间差异明显。

对昭通市极端降水时空特性的分析，能够在一定程度上掌握该市降水的基本特征，从而为未来的暴雨预测提供较大的帮助，进而减少因暴雨带来的洪涝灾害等及其他由此引发的次生自然灾害，为建设防灾安全措施提供了理论基础，更加有效地保障人民的生命和财产安全。

[1] 于文金, 阎永刚, 邹欣庆. 太湖流域暴雨时空特征研究[J]. 自然资源学报, 2012, 27(5):766-777.

[2] 崔肖林，陆建忠，陈晓玲，等. 不同气候条件的抚河流域SWAT径流模拟与验证[J]. 长江科学院院报，2015, 32(9): 14-20.

[3] 李 芸, 穆文彬. 西南地区暴雨时空分布特征分析[J]. 黑龙江大学工程学报, 2014，5(2):37-42.

[4] 周北平，史建桥，李少魁，等. 近53年长三角地区极端降水时空变化分析[J]. 长江科学院院报, 2016, 33(9): 5-9.

[5] 舒远华. 云南昭通市暴雨洪水特性分析[J]. 人民长江, 2012，43(增2):51-52，83.

[6] 宋昭义, 李晓燕, 宗德孝. 昭通市昭阳区盘河乡”7·14”特大暴雨洪水分析[J].水资源研究,2009,30(3):29-31.

[7] 罗奕群. 昭通市暴雨特性分析[J]. 水资源研究, 2011, 32(3):13-14.

[8] 姜云君, 付 靖, 刘少荣. 昭通一次区域性暴雨天气过程分析[J]. 云南地理环境研究, 2013, 25(3):34-38.

[9] 魏凤英. 现代气候统计诊断与预测技术[M]. 北京: 气象出版社, 2007.

[10]GERSTENGARBE F W, WERNER P C. Estimation of the Beginning and End of Recurrent Events within a Climate Regime[J]. Climate Research, 1999, 11(2):97-107.

[11]刘惠英, 丁文峰, 张平仓. 香溪河流域1965—2010年径流的变化趋势及突变分析[J]. 长江科学院院报, 2014, 31(4): 12-16.

[12]WANG H R, YE L T, LIU C M,etal. Problems Existing in Wavelet Analysis of Hydrologic Series and Some Improvement Suggestions[J]. Progress in Natural Science, 2007, 17(1):80-86

[13]李 淼，夏 军，陈社明，等. 北京地区近300年降水变化的小波分析[J]. 自然资源学报, 2011, 26(6): 1001-1011.

[14]彭 薇, 霍军军, 许继军. 鄱阳湖枯水期入湖径流变化特征分析[J]. 长江科学院院报, 2016, 33(3): 19-22.

[15]唐 见, 陈 进, 周建中. 长江上游保护区径流变化特征及其对气候因子响应的区域差异性研究[J]. 长江科学院院报, 2015, 32(6): 110-115.

[16]彭晓芬, 黄甫则, 周汝良. 云南省年均降雨量空间插值模拟方法比较[J]. 西南林学院学报, 2010, 30(5):25-28.

[17]虎雄岗, 谈树成, 金艳珠,等. 基于地形高程的云南省降雨量空间插值方法研究[J]. 热带地理, 2012, 32(4):370-377.

[18]李 新, 程国栋, 卢 玲. 空间内插方法比较[J]. 地球科学进展, 2000, 15(3): 260-265.

[19]昭通市年鉴编辑委员会. 昭通年鉴(2014)[R]. 云南芒市: 德宏民族出版社, 2014.

(编辑：黄 玲)

Spatial-temporal Distribution of Multi-scale Extreme Precipitationin Zhaotong City, Yunnan Province

LI Shen-dong

(Zhaotong Branch of Hydrology and Water Resources Bureau of Yunnan Province, Zhaotong 657000, China)

In this paper, the spatial and temporal distribution of extreme precipitation in different time scales(1 h, 6 h, 24 h) in Zhaotong, Yunnan Province were analyzed based on the data from 19 meteorological stations during 1969-2014. The Mann-Kendall trend test and wavelet transform were used to analyze the period and trend characters of three typical stations (Yudong, Xinhua, and Niujie). Then the Inversed Distance Weight method was used to interpolate the point data into the area. The results show that the trend of extreme precipitation from three typical stations is not obvious (p>0.05). The periods for these three typical stations are 30 a, 15 a and 5-7 a,respectively. The spatial distribution of the extreme precipitation differs greatly from north to south, which is larger in the North and smaller in the South.

extreme precipitation; spatial and temporal distribution; Mann-Kendall trend test; wavelet transform; Zhaotong City

2016-07-07；

2016-08-23

李绅东(1964-)，男，云南镇雄人，高级工程师，主要从事水文水资源研究与应用，(电话)13887065689(电子信箱)lshd789@126.com。

10.11988/ckyyb.20160686

2016,33(11):127-132

P333.2

A

1001-5485(2016)11-0127-06