试点情况下省域间碳汇量控制的合作微分博弈分析

余光英

摘要：发展林业碳汇不仅对林业投融资具有重要作用，而且对减缓和适应气候变化是一个不可或缺的工具或渠道。因为土地资源的有限性，发展林业碳汇需要逐步规划。采用随机微分博弈模型分析省域间在碳汇试点情况下的合作博弈情况，利用HJB方程解出反馈那什均衡解，然后利用数值仿真模型分析5种因素变化对林业碳汇量的影响，最后认为，对林业碳汇的发展需要立足当前做好工作，需要长期规划分阶段实施，需要提高管理能力及风险防范措施。

关键词：碳汇量；合作随机微分博弈；HJB方程；仿真

中图分类号：F326.2 文献标识码：A 文章编号：0439-8114（2016）04-1079-05

DOI：10.14088/j.cnki.issn0439-8114.2016.04.064

The Cooperative Differential Game Analysis of the Carbon

Sequestration Pilot between Provinces

YU Guang-ying

（Institute of Acounting and Finance， Wuhan College， Wuhan 430079， China）

Abstract：The development of forestry carbon sequestration plays an important role in forestry investment and financing，and it is also an indispensable tool or channel for mitigation and adaptation to climate change. Because of scarcity of resources， the development of forestry carbon sequestration need planning step by step. Based on stochastic differential game model，the cooperative game between provinces was analyzed，and then using the HJB equation to work out the feedback equilibrium solution，using the numerical simulation model to analyze five kinds of factors affecting the quantity of forestry carbon sequestration. Finally in view of forestry carbon sequestration，the suggestions of long-term plan and implement in stages， strengthening forestry carbon sequestration management and risk prevention measures，planning based on the current job were put forward.

Key words： carbon sequestration； the cooperative stochastic differential game； the Hamilton-Jacobi-Bellman equation； the simulation

1 研究综述

1.1 随机微分博弈研究的主要内容

随机微分博弈研究的内容主要体现在两方面。一是随机微分博弈的形式，这方面的研究主要围绕随机微分方程形式而进行。随机微分方程一般由两部分组成，即漂流项和随机项。一般随机微分方程的随机运动有布朗运动、高斯噪声、跳扩散等。对于随机运动的研究，有研究带跳的随机微分方程的，如王馨、郭冬梅等、阎登勋等[1-3]；有研究一类连续时间带切换参数的线性二次零和随机微分博弈问题的，如朱怀念等[4]；有研究一类连续时间不定仿线性二次型随机微分博弈的鞍点均衡问题的，如朱怀念等[5]；还有研究随机微分方程的随机指数稳定性问题的，如韩艳丽等、朱伏波、张微、宗小峰等[6-9]。二是随机微分博弈解的研究。微分博弈的解法分为开环纳什均衡（Open-loop Nash equilibrium）、闭环纳什均衡（Closed-loop Nash equilibrium）和反馈纳什均衡（Feedback Nash equilibrium）三种[10]。随机微分方程的解如果足够光滑，一般可以运用HJB方程进行；如果扩散项是退化的，则 HJB方程没有经典解，就要考虑粘性解等，如魏立峰等[11]对此类问题进行了研究。

1.2 随机微分博弈在碳汇相关领域的研究

碳汇相关领域中运用随机微分博弈进行研究的主要集中在以下几个方面。一方面是运用随机微分博弈模型研究排污税、碳税及环境政策，如Benchekroun等、Rubio等、Yanas等[12-14]对此进行了研究。另一方面是运用随机微分博弈模型研究二氧化碳交易许可证的规则问题，如Germain等、Bernard等[15，16]对此进行了研究。再另一方面是运用微分博弈模型研究气候变暖问题，如Rubio等[17]对此进行了研究。另外就是在酸雨、污水排放中的研究，如Fernandez[18]对此进行了研究。

梳理已有文献，可以发现在碳汇相关领域运用随机微分博弈进行研究主要限于环境及可持续方面，将其运用于研究碳汇量的控制中并不多。由于碳汇的供给及交易都具有随机的特性，可以借鉴随机微分博弈，所以在借鉴随机微分博弈的已有研究成果基础上本研究从合作微分博弈的角度研究碳汇交易机制中的碳汇量的控制，以期为碳汇市场的发展提供可参考的建议。

2 基本模型

2.1 基本情况

要解决碳汇交易机制的问题，就要解决交易的标底、交易的主体、交易的平台等问题。欧洲排放交易系统中碳排放许可发放太多，以致于市场没有流动性，影响了碳交易市场的发展。所以要保证碳市场的平稳发展，确定要排放的额度非常重要，林业碳汇的发展也不例外。

有限的土地资源要在农用地、建设用地等方面平衡，必须要进行合理的规划。但是无论怎样规划，用以发展林业碳汇的资源是有限的。国家林业局公布的第八次全国森林资源清查成果显示，中国森林覆盖率为21.63%；从中国国土资源部查得资料表明2013年中国未利用地为27.9%。虽然中国森林覆盖率低于世界平均水平，国家规划要逐步提高森林覆盖率，但不是无限制的，所以林业碳汇的总量是有限的，因此规划及规划后的管理非常重要。由于中国是按省进行土地利用规划、植树造林地规划，所以本研究以省区域为例来进行碳汇量目标优化分析。

2.2 基本假定

假定1，在试点情况下，有些省份是额定的任务，而有的省份则是弹性的，但各省份在碳汇发展方面是有规划的。在此考虑两个省份在博弈中为参与人i，i=1，2。

假定2，假定两省份是单一经济（环境）模型。

假定3，假定考虑的时间是t，t∈[0，T]。

假定4，参与人i在时间t的碳汇造林面积为qi（t），i=1，2，t∈[0，T]。

假定5，参与人i有碳汇造林面积qi（t）时所能吸收的净碳汇为ei，ei=hi（qi（t）），i=1，2。假定碳汇量随着碳汇林业面积的增加而严格递增，即ei是严格递增的。

假定6，参与人i碳汇造林面积qi（t）时，所带来的净收入为ri（qi（t））。由于 ei=hi（qi（t）），qi（t）=hi-1ei（t），故 ri（qi（t））=ri（hi-1ei（t））。记Ri（ei（t））=ri（hi-1ei（t）），是递增的凹函数，收益最终会下降，且Ri（0）=0，i=1，2。假定：Ri（ei（t））=αi ei（t）-■e■■（t）。

假定7，B（t）是维纳过程。

假定8，在时间t的林业碳汇存量为s（t）。这是由以前植树造林、林业维护及砍伐等因素造成的，是已有造林碳汇理论上的存量。

假定9，由于维护林业碳汇存量参与人i所花费的成本为Di（s（t）），假定其为单调递增的凸函数，i=1，2。Di（s（t））=■βis2（t）。假定参与者2是在试点范围内有额定的减排量或碳汇量，参与者1不在指定的进行碳汇减排的范围内，但其可以参与其他地区碳汇交易。这样参与者1便存在一个搭便车的行为，假定其维护成本为0，即假定β1=0，β2≠0。

假定10，贴现率为r。e-rt是贴现因子。

假定11，参与人i的林业碳汇的边际影响均是相同的，均为1，即碳汇量的值就是效用的值。

假定12，碳汇存量从理论转化为实际的转化率为常数？着，？着>0。

假定13，由于现实中有些不可预知的突发事件，比如天气、自然灾害、人为因素等，假定这些因素对林业碳汇存量的影响为常数？滓，？滓≥0。

2.3 合作随机微分博弈模型

某时刻碳汇量=林业碳汇的增加量（边际量）+已有碳汇林的转化量+由于自然灾害/人为灾害/管理的变化/政策的变化等导致的林业碳汇的变化量。

假设下面的线性微分方程为净碳汇积累的动态过程：

ds（t）=（e1（t）+e2（t））+？着s（t）+？滓s（t）dB（t）

s（0）=s0

假定参与人i，i=1，2的期望目标函数为：

J1+J2=■E{■■[e-rt（Ri（ei（t））-Di（s（t）））dt]}

3 合作博弈解

考虑下面情况的反馈纳什解。

ds（t）=u（e1（t）+e2（t））+？着s（t）+？滓s（t）dB（t） （1）

s（0）=s0 （2）

J1+J2=■E{■■[e-rt（Ri（ei（t））-Di（s（t）））dt]}（3）

命题1策略{？准■■（t，s），？准■■（t，s）}构成随机微分博弈问题（1）（3）的一个反馈纳什均衡，如果存在连续函数w（t，s）：[0，T]×R→R，且有连续偏导数ws（t，s），wss（t，s），i=1，2满足以下Hamilton-Jacobi-Bellman-Fleming方程。

rw（t，s）-■wss（t，s）=■E{■[？琢i ei（t）-■e2i（t）-■？茁is2（t）]+ws（t，s）[（e1（t）+e2（t）+？着s（t））]}

w（T，s）=2gs2

？准■■（t，s）是参与人i，i=1，2的最优控制。

命题2对合作随机微分博弈（1）（3）博弈的参与人1和参与人2的反馈纳什均衡解分别为：

e1（t）=？琢1+[？琢s（t）+b]

e2（t）=？琢2+[？琢s（t）+b]

w（t，s）=■as（t）2+bs（t）+c

其中0=（r-？滓2-2？着）a-2？琢2+（？茁1+？茁2） （4）

0=rb-（？琢1+？琢2）？琢-2？琢（t）b（t）-？着b （5）

0=rc-■（？琢12+？琢22）+（？琢1+？琢2）b-b2 （6）

因为ei严格递增，由（4）得：

a=■

由（5）得：

b=■

由（6）得：

c=■

由命题2中e1（t），e2（t）的表达式知道，反饋纳什均衡策略e1（t），e2（t）和当前时间和状态s有关，与状态s的过去值无关。所以，反馈策略e1（t），e2（t）是马尔科夫的。

4 數值仿真分析

本研究数值仿真用matlab2012b完成。根据对ds（t）影响的因素不同，仿真分5种情况进行，具体5种情况的赋值见表1。

4.1 t值不同

根据表1，假定时间分别是10个月，50个月，100个月，其他要素相同，采样步长取1，得到图1中的a，b，c图。图形表明，如果规划的时间越长，碳汇存量越是集中在最后的时间增多，规划的时间越短，越是早点开始增加，规划的时间与突击应付的程度相关。

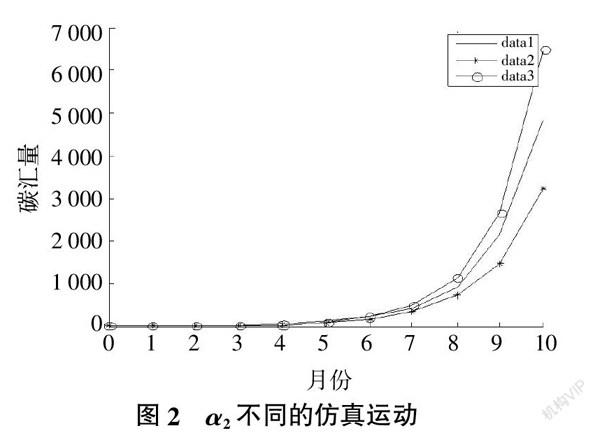
4.2 系数？琢2不同

根据表1，假定？琢2分别为0.6，0.7，0.8，步长为1，时间为10个月，其他要素相同，得到图2的三条仿真曲线。从图形中可以看出，在前面5个月，碳汇存量的增加非常小。从五月开始，碳汇量开始迅速增加，越是接近规划结束的时间，增加得越大。并且碳汇量增加与？琢2的大小不存在严格的相关关系。

4.3 ？着值不同

根据表1，？着取0.8，0.7，0.6，其他要素相同时仿真图形分别是图3中的值1，值2，值3对应的图形，从图3可以看出，在前面5个月，碳汇存量的增加非常小，随后碳汇量开始迅速增加，特别是接近规划结束的一个月增加得更多。？着值的大小对碳汇存量的影响在起初的很长一段时间内不具有相关性，但是临近规划结束的时候却呈现了相关性，此时？着越大，碳汇存量越小。

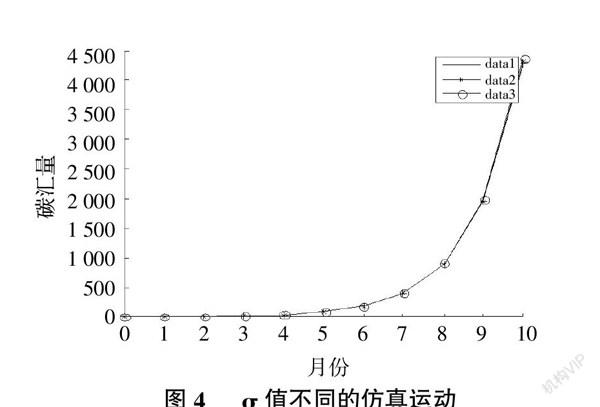
4.4 ？滓值不同

根据表1，？滓分别取0.2，0.1，0.01，其他要素相同，步长取1，得到值1，值2，值3的仿真图形（图4）。从图4中可以看出这三条线几乎是重合的，所以说？滓值的大小对碳汇存量的影响不随其值的大小而产生明显的影响。

4.5 ？茁2值不同

根据表1，假定？茁2分别为0.4，0.3，0.2，步长为1，时间为10个月，其他要素相同，得到图5。从图5中可以看出，前面5个月碳汇存量的增加非常小。从五月开始，碳汇量开始迅速增加，越是接近规划结束的时间，增加得越多。但碳汇量的增加与？茁2的大小不存在相关关系。

5 结论及建议

5.1 立足当前采取措施

根据反馈那什均衡解是马尔科夫的，过去的状态对现在的影响不大。无论该省过去在碳汇上采取何种策略和处于何种地位，对当前都没有明显的激励或者鞭策作用。那么碳汇的发展就应该立足当前采取措施。在中国还没有强制减排的情况下，对于林业碳汇的态度和策略是和二氧化碳减排紧密相连的，所以在立足当前采取措施时，特别需要与碳减排协同创新。

5.2 长期规划分阶段执行

t值越小，即规划的时间越短，能够进行拖延的时间就越有限，碳汇开始大幅增加的时间相对长期而言就越早；t值越大，即规划的时间越长，碳汇开始大幅增加的时间就越晚，即有大量的时间等待或观望，在临近规划结束要检查成果时会有大量的增加。综合这两种情况，碳汇发展的规划应该长期规划，短期分阶段执行，以便让碳汇量尽早地可持续增加，而不是在规划期临近结束时突然大幅增加。

5.3 提高管理能力做好风险防范

？滓2越大，碳汇存量越大，这与碳汇的收入效应相关，这需要整个碳汇体系良好的发展。晚期的？着值越大，碳汇存量越小，因此晚期需要防范管理的疏忽或懈怠。？滓值的大小与碳汇存量的多少没有严格的相关关系。所以综合这些情况，说明需要做好碳汇控制与发展中的风险管理与防范，勿因林业的自然灾害或其他灾害在发展碳汇林业方面畏首畏脑。

需要说明的是本结论是在单一经济、合作情况的假定下得出的，与现实不完全相符，因此需进行进一步的研究。

参考文献：

[1] 王 馨.非Lipschitz条件下带跳的随机微分方程解的轨道唯一性和非爆炸性[D].北京：北京理工大学，2015.

[2] 郭冬梅，井 帅，汪寿阳.带跳的分数倒向重随机微分方程及相应的随机积分偏微分方程[J].中国科学数学，2014，44（1）：73.

[3] 阎登勋.带泊松跳的随机时滞发展方程的适定性、稳定性、整体吸引集和可控性[D].南京：南京师范大学，2014.

[4] 朱怀念，植璟涵，张成科，等.带Markov切换参数的线性二次零和随机微分博弈[J].系统科学与数学，2013，33（12）：1391-1403.

[5] 朱怀念，张成科，李云龙，等.一类不定仿线性二次型随机微分博弈的鞍点均衡策略[J].广东工业大学学报，2012（3）：35-38.

[6] 韩艳丽，高 岩.线性微分博弈系统的识别域判别[J].控制与决策，2015，30（7）：1329-1332.

[7] 朱伏波.Markov切换随机系统的稳定性与镇定性研究[D].上海：上海交通大学，2014.

[8] 张 微.非耦合、弱耦合正倒向随机微分方程的高阶数值方法及误差估计[D].济南：山东大学，2014.

[9] 宗小峰.随机微分方程的数值分析及随机稳定化[D].武汉：华中科技大学，2014.

[10] 于 伟.一类非对称环境问题的随机微分博弈研究[D].天津：天津大学，2011.

[11] 魏立峰.随机最优控制相关的HJB方程及弱解研究[D].济南：山东大学，2009.

[12] BENCHEKROUN H，LONG N V. Efficiency-inducing taxation for polluting oligopolists[J]. Journal of Public Economics， 1998， 70（2）：325-342.

[13] RUBIO S J，ESCRICHE L. Strategic pigouvian taxation，stock externalities and polluting non-renewable resources[J].Journal of Public Economics，2001，79：297-313.

[14] YANASE A.Dynamic games of environmental policy in a global economy：Taxes versus quotas[J].Review of International Economics，2007，15（3）：592-611.

[15] GERMAIN M，STEENBERGHE V V. Constraining equitable allocations of tradable CO2 emission quotas by acceptability[J]. Environmental and Resource Economics，2003，26（3）：469-492.

[16] BERNARD A，HAURIE A，VIELLE M，et al. A two-level dynamic game of carbon emission trading between Russia，China， and annex B countries[J]. Journal of Economic Dynamics & Control，2008，32（6）：1830-1856.

[17] RUBIO S，CASINO B. Self-enforcing international environmental agreements with a stock pollutant[J]. Spanish Economic Review，2005，7（2）：89-109.

[18] FERNANDEZ L. Trades dynamic solutions to trans boundary pollution[J].Journal of Environmental Economics and Management，2002，43（3）：386-411.