相关高维数据流在线监控方法研究
卞水仙,訾雪旻
(天津职业技术师范大学理学院,天津300222)
相关高维数据流在线监控方法研究
卞水仙,訾雪旻
(天津职业技术师范大学理学院,天津300222)
针对高维数据流在线监控问题,对其所对应的控制图方法进行研究,阐述了在高维数据流存在相关性的情况下,以CUSUM控制图为基础,采用在高维数据流相互独立的条件下提出的4种方法,根据单边统计量检验和给定实际变点,找出漂移大小不同情况下控制图的报警时间。经过多次模拟并运用统计学理论,比较4种方法的稳健性与灵敏度,得出拟合优度方法能较好地平衡失控时控制图统计量的灵敏度与稳健性,总体上达到最优。
相关性;CUSUM;拟合优度;异致性混合检验;次序统计量
随着工业的迅速发展,近年来对于高维数据流监控问题的研究逐渐成为热点[1-4]。工业上为减少资源的浪费及提高产品合格率,其相关控制图的选取就变得尤为重要。控制图的作用就是当事故发生时,能够从控制图中很快找到报警时间,减少损失。Healy[5]与Croisier[6]研究了当数据流在相互独立的情况下的多元累计和控制图[7]。Cai J和Jin[8]及Donoho和Jin[9]研究了在异质性与异方差性的参数下,数据流不受影响的概率比例问题。本文在已有研究的基础上,将此方法运用到相关高维数据流的研究中。Cai Jeng和Jin分析了在稀疏与稠密情况下,不受影响的因素对异质性混合问题难度的影响,并以似然比检验为基础准确给出了数据流的可检测范围与不可检测范围。以上研究均是通过假定数据流是相互独立的情况下,运用多种控制图进行监控。而实际中,这些数据流往往是具有相关性的。因此,本文对已有的4种方法进行分析,并通过多次模拟比较它们的稳定性与灵敏度,进而寻求最优方法。
1 提出模型
假定在t时刻监控p个数据,记为Xt=(X1t,X2t,…,Xp)tT,满足模型Xt=U+Zt。其中U是可控时p条数据流的均值向量可控情况下Zti~idN(pμ0,,似然比检验统计量为(σii=1),由于其对称且正定的性质,可分解为Σ= LTL。根据蒙特卡罗产生相关随机数的方法[10],假定Xkt表示第k条数据流在t时刻的观测值,其中1≤k≤p。假定Xk在t=τk时刻发生变化,均值从0漂移到μk,此时可以考虑2种情况:①p条数据流在同一时刻发生漂移;②数据流发生漂移时刻不同。假定报警时间为T,本文的目的是在数据流发生漂移后,尽快找出报警时间T。
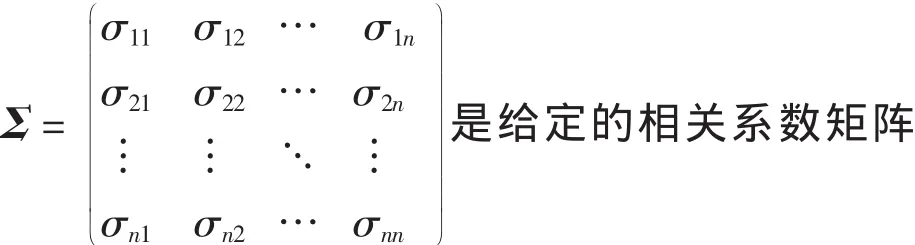

2 异质性混合检验
2.1高标准统计量
在文献[8-9]中,作者分析了在稀疏与稠密2种情况下,采用似然比检验的方法,确定了数据流的可检测范围和不可检测范围并给出其不受影响的比例公式。假定H0:u=0、H1:u>0,当可控时Xk~N(p0,Σ),失控时Xk~N(pμk,Σ)。高标准统计量公式为:式中为Xk的累积分布函数,且p(1)<p(2)<…p(n)是次序统计量。当统计量很大时,拒绝原假设,则报警时间
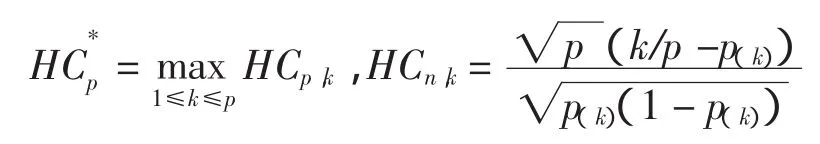
2.2拟合优度检验
Zhang J[11]与文献[12]在似然比检验的基础上提出了更加稳健的拟合优度检验。结合文献[11]中的方法和高标准统计量的可检测范围,可以定义拟合优度的单边统计量[13-14]为:
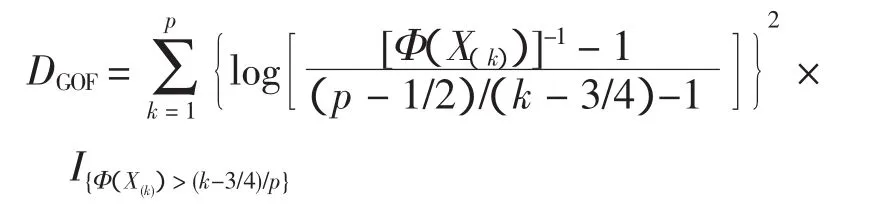
式中:(I·)表示示性函数;(k-3/4)/p与X(k)的累积分布函数相关,且X(1)<…<X(p)是次序统计量。
用S(kt)代替X(kt),可得等式为:
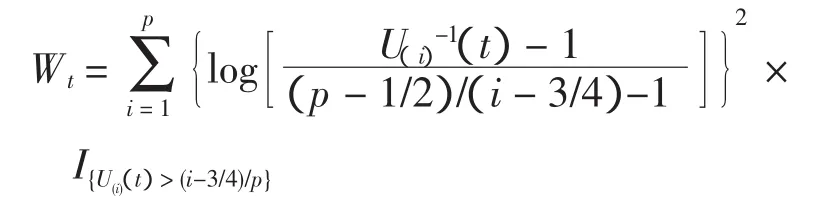
式中:U(it)是关于S(kt)与uk的函数且为S(kt)的累积分布函数,U(1t)<…<U(pt)为次序统计量。
定义报警时间为Tnew=inf{t:Wt≥L},在不同控制图中,L分别取可控情况下95%的上分位点。
3 大量数据流在线模拟
根据蒙特卡罗的方法选取多维相关数据流,生成Xp×t的矩阵。可控时,失控时是相关系数矩阵;之后根据CUSUM统计量的原理,得到CUSUM统计量S(kt),经过n次重复得到前2种方法的控制线L(取可控时统计量的95%)。假定实际变点发生的时刻为τk,重复以上模拟,记,计算其方差及错误率。根据异质性混合检验,将S(1t),S(2t),…,S(pt)与X1,X2,…,Xt的问题联系起来,可用S(kt)代替单边统计量Dhc与DGOF公式中的X(kt),分别求出可控时的单边控制线L,再经过多次模拟,计算报警时间及其方差与错误率[15]。在不同的漂移大小情况下,比较4种方法的稳健性与灵敏度。时刻t=2时CUSUM统计量(u= 0)如图1所示。图1给出了可控条件下,在某一时刻的p个CUSUM统计量。时刻t=102时,CUSUM统计量(u=0.5)如图2所示。
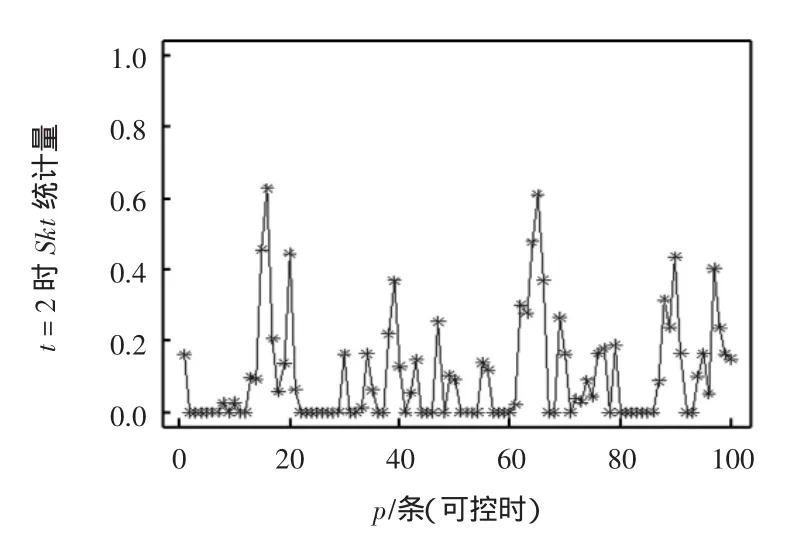
图1 时刻t=2时CUSUM统计量(u=0)

图2 时刻t=102时,CUSUM统计量(u=0.5)
由图1与图2的对比可知,随着漂移的发生,CUSUM统计量波动增大,总体上取值增大。
uk=0.2、μk=0、p=100时,4种方法的单边统计量如图3所示。由图3知,在可控情况下,Dsum与DGOF灵敏度较好,Dhc最差。

图3 uk=0.2、μk=0、p=100时4种方法的单边统计量
uk=0.2、p=100、μk=0.5、变点τ=100时,4种方法的单边统计量如图4所示。由图4可知,Dsum与DGOF较为灵敏,Dmax稳健但不够灵敏。

图4 uk=0.2、p=100、μk=0.5、变点τ=100时4种方法的单边统计量
不同漂移大小得到的报警时间T如表1所示。由表1可知,Tsum表现较好;但随着漂移的逐渐增大,拟合优度的报警时间逐渐趋于最优;Tmax对于漂移较小时性能较好,但反应不灵敏;Tnew在Thc的基础上进行改进,性能较好。
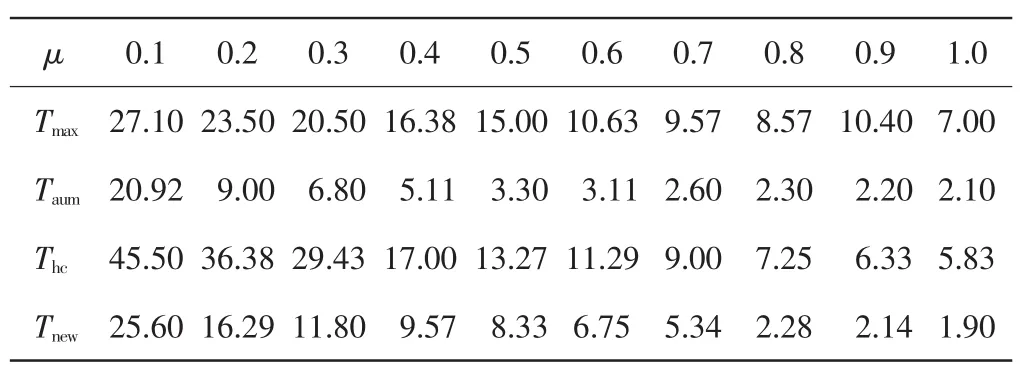
表1 不同的漂移大小μ得到的报警时间T
4 结束语
本文通过蒙特卡罗方法生成随机变量,进行多次模拟分别计算在不同漂移大小情况下的Dsum、Dmax、Dhc和DGOF,并根据设定的控制线找出报警时间,比较几种方法的稳健性与灵敏度。结果表明:当漂移0<μ<1时,随着漂移逐渐增大,Tnew逐渐趋于最小,Tsum在漂移较小时表现一直最好,但随着漂移的逐渐增大,Tsum逐渐次于Tnew。同时根据图3和图4可知,Dsum的稳健性最差,Dhc的稳健性最好但反应不灵敏,总体上DGOF能做到灵敏度与稳健性较好地平衡,因此拟合优度的方法较为合理。
[1]吴庆耀.高维数据流的若干分类问题及算法研究[D].哈尔滨:哈尔滨工业大学,2013.
[2]周彦.基于经验似然的拟合优度检验及推广应用[D].长春:东北师范大学,2008.
[3]于怡.高维数据变量选择的几点研究[D].上海:复旦大学,2013.
[4]赵俊琴.基于Lasso的高维数据线性回归模型统计推断方法比较[D].太原:山西医科大学,2015.
[5]HEALY J D.A note on multivariate CUSUM procedure[J]. Technometrics,1987,29(4):409-412.
[6]CROISIER R B.Multivariate generalizations of cumulative sum quality control schemes[J].Technometrics,1988,30(3):291-303.
[7]GOLOSNOY V,RAGULIN S,SCHMID W,et al.Comparison of multivariate cusum charts[J].AStA Advances in Statistical Analysis,2009,93(3):263-279.
[8]CAI T T,JENG X J,JIN J S.Optimal detection of heterogeneous and heteroscedastic mixtures[J].Journal of the Royal Statistical Society:Series B,2011,73(5):629-662.
[9]DONOHO D,JIN J.Higher criticism for detecting sparse heterogeneous mixtures[J].The Annals of Statistics,2004,32(3):962-994.
[10]文德智.蒙特卡罗模拟中相关变量随机数序列的产生方法[J].物理学报,2012,61(22):41-48.
[11]ZHANG J.Powerful goodness-of-fit tests based on likelihood ratio[J].Journal of the Royal Statistical Society:Serie B,2002,64(2):281-294.
[12]彭超.拟合优度检验统计量的研究及在质量控制中的应用[D].秦皇岛:燕山大学,2012.
[13]杨振海.拟合优度检验[M].合肥:安徽教育出版社,1994.
[14]王重,刘黎明.拟合优度检验统计量的设定方法[J].统计与决策,2010(5):154-156.
[15]WANG K B,JIANG W.High-dimensional process monitoring and fault isolation via variable selection[J].Journal of Quality Technology,2009,41(3):247-258.
[16]薛毅,陈立萍.统计建模与R软件[M].北京:清华大学出版社,2007.
Online monitoring methods for correlated high-dimensional data streams
BIAN Shui-xian,ZI Xue-min
(School of Science,Tianjin University of Technology and Education,Tianjin 300222,China)
As to the problem of the online monitoring of the correlated high-dimensional data streams,corresponding control charts are analyzed in this article.When the existing correlation of the data streams,based on CUSUM(cumulative sum),four charts are used,namely the maximum of CUSUM statistics,sum of CUSUM statistics,higher criticism statistic,good-offit test statistic to solve the problem of alarming time out of control.According to the one-side statistic test,the true change point is given to find the alarming time of the control charts for different drifts.After many simulations,by using the statistics theory,the robust and sensitivity of four methods are compared.The research shows that the good-of-fit test statistic can better balance the sensitivity and robust of the control charts for out of control.In a word,the good-of-fit method is better to achieve the optimal overall.
correlation;CUSUM;good-of-fit test;heterogenous mixture test;order statistics
TP277
A
2095-0926(2016)03-0047-03
2016-06-12
国家自然科学基金资助项目(11271205).
卞水仙(1990—),女,硕士研究生;訾雪旻(1977—),女,副教授,博士,研究方向为数理统计.
——拟合优度检验与SAS实现

