基于自适应纯形模拟退火法一维大地电磁测深视电阻率和相位反演研究
孙欢乐,王世彪,郭荣文,周绍民,柳建新*
(1.中南大学 a.地球科学与信息物理学院,b.有色资源与地质灾害探查湖南省重点实验室,长沙 410083;2.广东有色工程勘察设计院,广州 510080)
基于自适应纯形模拟退火法一维大地电磁测深视电阻率和相位反演研究
孙欢乐1a,1b,王世彪2,郭荣文1a,1b,周绍民1a,1b,柳建新1a,1b*
(1.中南大学 a.地球科学与信息物理学院,b.有色资源与地质灾害探查湖南省重点实验室,长沙 410083;2.广东有色工程勘察设计院,广州 510080)
针对大地电磁测深反演中线性化方法容易陷入局部极值,而全局优化方法收敛慢等问题,这里采用自适应纯形模拟退火综合优化方法进行大地电磁测深数据反演。该优化方法综合了下降纯形法和模拟退火法各自的优点,已被证明具有全局搜所能力和收敛速度快的特点,并且实现了视电阻率和相位同时反演,减小多解性的同时提高了反演的分辨率。通过H、K和HKH型模型的数值计算,验证了这种综合优化方法的搜索效率和全局收敛性;所有模型合成数据的反演结果都能较好地反映真实模型的结构特征。对于中间层为相对高阻的模型,虽然相对其他层结构恢复差些,但是反演后该层结构基本得到恢复。
大地电磁; 视电阻率; 相位; 下降纯形法; 模拟退火法; 自适应纯形模拟退火法
0 引言
大地电磁测深(MT)是发展较早的一种地球物理勘探方法,在探测地热、金属矿勘探和地震预报等方面得到广泛地应用[1-2]。近些年来该方法发展迅速,许多学者一直致力于大地电磁测深反演方法的研究,对于一维MT,目前应用最多的反演方法大都属于线性或拟非线性方法(马夸特方法和广义逆矩阵法)[3-4]。但是大地电磁测深反演问题是非线性问题,而且具有非唯一性,线性或拟非线性反演方法依赖于初始模型的选择,容易陷入局部极值,最终把局部最优解当作全局最优解,导致后期资料的解释不准确[5]。由此,专家学者们提出了应用非线性全局最优方法求解地球物理反演问题[6],其中,模拟退火法得到了许多地球物理学家的关注和重视[7]。模拟退火法受统计热力学现象的启发[8],1953年Metropolis等人[9]将模拟退火算法的思想提出,但当时并未得到广泛地应用,30年后,Kirkpatrick等人[10]将模拟退火法的思想成功地应用于组合优化问题,随后模拟退火法得到了很大的发展。在地球物理领域,Rothman[11-12]在地震资料处理的剩余静校正问题中首次应用了模拟退火法的思想,其后Sen和Stoffa等人[13-14]将其用于一维地震波形反演、一维电测深反演。后来,模拟退火法在MT[15]、重力磁法勘探资料等反演问题中[16]得到了广泛研究与应用。
实际中的地球物理反演是一个多参数、非线性优化问题,所采用的目标函数,即衡量由理论模型得出的正演响应值与观测值的吻合程度,常具有多个局部极值[17],虽然模拟退火法随机搜索,可以避免局部极小值的影响,最终得到全局最优解,但是模拟退火法优化方法是在可行解空间中随机搜索,通过Metropolis法[18]来控制新解的取舍,所以其迭代速度相对较慢。此外,模拟退火法是否收敛于全局最优解受多种因素的影响,比如初始温度的选择、温度的下降模式、随机扰动的方式等。温度选择越高,下降越慢,模型空间搜索的越彻底,可以避免陷入局部极小模型,但是耗费大量的计算时间,所以模拟退火法的全局收敛较慢。
针对上述问题,作者在研究地球物理各种优化算法的基础上,引进了自适应纯形模拟退火综合方法(Adaptive simplex simulated annealing,ASSA),该方法是纯形下降优化方法和模拟退火法的有机结合,最初由Press等[19]提出解决NLP问题。纯形下降法最早由 Spednley等人提出,Nelder 等[20]作了改进,纯形下降优化方法可以实现直接快速地搜索到极小值,但是容易受到局部极小值的影响,所以容易陷入局部极值。因此,可以结合二者的优点,协同快速地求解反演问题的全局最优解,自适应纯形模拟退火优化方法已在一维声波和地声学反演方面得到了成功地应用[17,21]。一维MT反演通常只利用视电阻率或者阻抗幅值,往往忽略阻抗相位,其实阻抗相位包含着大量的地下电性信息。对于一维地电结构来说,相位和视电阻率资料不是相互独立的,其具有一定的相关性[2]。作者利用视电阻率数据和阻抗相位数据进行同时反演,二者同时反演可以减小反演的多解性,提高分辨能力,还对压制静态位移具有积极的意义。这里通过对一维大地电磁数据测深反演,验证了自适应纯形模拟退火综合反演方法的全局搜索能力和效率,同时验证了视电阻率数据和阻抗相位数据同时处理可以提高反演的精度。
1 一维大地电磁测深正演
1.1 正演公式
假设地下电性结构是水平层状分布的,如果地电结构共有n层,则有2n-1个参数, hi(i=1,2,…,n-1)代表第i层的厚度;ρi(i=1,2,…,n)代表第i层的电阻率,最后一层为均匀半空间,则hn=∞。计算视电阻率ρs和阻抗相位φ的表达式如式(1)、式(2)所示[2-3]。
(1)
(2)
其中:ω表示角频率;μ0表示导磁率;Z表示地面的波阻抗值。
公式(3)建立了视电阻率、阻抗相位和频率及层参数间的关系[5]。
ρs=f(h1,ρ1,h2,ρ2,…,hn-1,ρn-1,ρn,f)
φ=g(h1,φ1,h2,φ2,…,hn-1,φn-1,φn,f)
(3)
1.2 目标函数
目标函数(能量函数)[22]通过模型正演响应值、观测值及其数据噪声的标准差来建立,具体表达式如式(4)所示。
(4)
其中:ρdi和φdi分别为频点fi的观测视电阻率值、观测阻抗相位值;ρmi和φmi分别为频点fi的模型视电阻率值、模型阻抗相位值;σρi和σφi分别表示相应第i个视电阻率或相位数据噪声的标准方差;n为频点个数。
2 模拟退火算法
模拟退火法(Simulated Annealing, SA)来源于热力学的退火原理[23-25]:高温物体具有一定的自由能,物体内部晶体杂乱无序,处于十分不稳定的状态;不断地降低物体的温度,随着温度的降低物体的自由能也有所下降,物体内部晶体从无序逐渐有规则的排列。当温度下降到最小值时,此时物体内部的自由能达到最小,物体内部的晶体有序排列,整个物体处于一种非常稳定的状态。温度最低时,物体所具有的最小自由能就是优化问题所求得最优解。
模拟退火算法的实现步骤为:
1)设置全局可行解的搜索空间。在可行解的空间中初始化一个模型M0、设定起始温度T0、最大迭代次数NT、拟合误差阀值e、已迭代次数k等参数并令k=0。设定温度下降方式,不同反演问题选择不同的温度下降方式(指数下降型和双曲线下降型)。
2)对第k次迭代的模型参数值Mk,计算温度Tk和目标函数值E(Mk),对模型Mk在可行解搜索空间里进行随机扰动形成新模型Mk+1,并计算目标函数E(Mk+1),E为目标函数。
3)采用Metropolis抽样准则对模型选择。令ΔE=E(Mk+1)-E(Mk),若ΔE<0,新模型Mk+1被接受;否则,新模型Mk+1按照概率P(ΔE)=exp(-ΔE/T)被接受,产生随机数η,η∈[0,1],若η≤P,则新模型Mk+1被接受,否则,拒绝接受新模型Mk+1,转步骤2)。
4)计算目标函数E(Mk+1),如果E(Mk+1) 下降纯形法(Downhill Simplex, DS)是一种高效的近似梯度寻优方法,该方法不需参数空间导数或灵敏度矩阵[26-27]参加运算,可以直接、快速地沿极小值的方向搜索,但容易陷入局部的极小值。其思想是在R维模型空间中,假定一个由R+1个点组成的初始纯形空间(如图1(a)R=3),每个点都对应一个函数值并按照其大小依次排列[21],得到最高点(函数值最大)和最低点(函数值最小),然后对纯形进行反射、收缩及延伸等步骤并计算对应的函数值,舍弃恶化点,保留优化点,最终构造成新的纯形空间,由此逐步逼近极小值点。 下降纯形法步骤为[21,28]: 1)算法开始,具有最大函数值的点(高点)通过R维单纯形的背向面移到另一侧(图1(b))以改善高点的函数值。 2)若反射后的函数值比最大值要小,那么这个点就被接受。若反射后的函数值在纯形中最小,那么新的点将从高点的背向反射并延伸两倍(图1(c))。 图1 下降纯形法示意图[19]Fig.1 Downhill simplex method diagram(a)初始纯形; (b)反射;(c)反射和延伸;(d)收缩;(e)多向收缩 3)若新的点在纯形中仍然具有最大的函数值,那么这个反射后的点将被丢弃,同时从高点沿反射面方向的收缩(图1(d))。 4)若上述所有的步骤都无法使函数值降低到比最大值小,那么纯形上R个点将沿低点方向进行两倍的收缩(图1(e))。 重复以上四个步骤直到在纯形中最高点函数值Ehigh和最低点函数值Elow之间满足式(5)收敛标准[27]。 (5) 在反演中,这里采用ε=10-5。 自适应纯形模拟退火法(ASSA)是一种综合优化算法,综合了下降纯形法(DS)和模拟退火法(SA)[29]。模拟退火法是一种利用Metropolis准则在可行解空间随机搜索的优化方法,它可以避免局部极小值的干扰,最终可以搜索到全局最优解,但其耗费大量时间、收敛速度慢[28]。下降纯形法能直接、快速地搜索到极小值,但当目标函数有不止一个极小值时,不同的初值选择会导致不同的反演结果,容易导致局部最优解代替全局最优解[30]。因此,综合二者的优点,既可以提高搜索效率,又避免了陷入局部极小值。 自适应纯形模拟退火法的基本思想为对于初始模型M0,首先采用纯形下降法沿着梯度方向搜索到一个极小值点,然后利用模拟退火法在可行解空间内随机搜索,使其跳出该局部极小值点,当搜索到一个比该极小值点更小的点时,立刻以新的极小值点为初始点再次采用纯形下降法搜索新的极小值点附近的另外一个极小值点,如此交叉进行纯形下降法和模拟退火法,直到满足精度终止条件,算法结束。 自适应纯形模拟退火优化算法的实施步骤[28]: 1)设定初始值。设置控制参数T(温度)的初值T0、初始步长V0、控制精度τ、最大迭代次数NT、已迭代次数k等参数并令k=0。随机产生R+1个点的初始模型,其中能量值最小模型为M0,令EOPT=E(M0),MOPT=M0。 2)下降纯形法搜索。以M0为初始点,采用下降纯形算法搜索该点周围的一个极小值Mmin,并令Mk=Mmin,E(Mk)=E(Mmin),MOPT=Mmin,EOPT=E(Mmin)。 3)模拟退火法。以Mk为初始点采用模拟退火算法,计算温度Tk,在可行解搜索空间随机产生新点Mk+1=Mk+rV0,其中r为随机数,r∈(-1,1),计算E(Mk+1)。 4)Metropolis接受准则。若E(Mk+1)≤E(Mk),新解Mk+1被接受;否则,新解Mk+1按照概率P(ΔE)=exp(-Δ/T)被接受:产生随机数η,η∈[-1,1],若η≤P,则新解Mk+1被接受。 5)重复步骤3)和步骤4),直到E(Mk+1) 6)改变温度Tk+1=update(Tk),并令k=k+1。 自适应纯形模拟退火优化当中,下降纯形法反射、延伸和收缩等每个步骤的函数值计算之前,对该模型的各参数设置Cauchy分布的扰动[21,26]。 (6) c=λ1tan(λ2π/2) (7) 式中:λ1和λ2是随机分布在[-1,1]上的变量。 温度的下降方式影响到自适应纯形模拟退火法的收敛性,ASSA中温度利用指数下降模式,比较符合退火的实质[21],即 Tk=αkT0 (8) 式中:k为迭代次数(降温次数);α是小于1的常数;T0为初始温度,初始温度应该使80%以上的随机扰动都被接受;Tk为迭代k次时的温度;这里α取值0.998。 为了验证自适应纯形模拟退火法优化方法的搜索能力和全局收敛性,作者设计H型、K型和HKH共3个地电模型,模型参数设置如表1所示。频率点数为40个,本文中的电阻率的单位为Ω·m,层厚度单位m。 表1 模型参数 5.1 计算实例对比 我们选择一个H模型,参数设置如表1所示,分别利用下降纯形法、模拟退火法和自适应纯形模拟退火法进行反演,试比较三者的反演速度和拟合精度。实际采集的野外资料都含有一定的噪声,这里采用理论合成模型加入适当的噪声模拟野外实测数据,对该模型的正演响应(视电阻率和相位)加入2%的高斯噪声后再反演,三种反演方法结果如表2所示。 从表2可以看出,对于H型曲线三种反演方法都可以找到一个合适的结果,但在个别参数上存在一些误差。DS反演中最佳模型参数和真值相差最大不到10.09% ,拟合差为40.57 ,反演时间相对较短;SA反演中最佳模型参数和真值相差最大不到9.89% ,拟合差为39.36 ,反演时间相对较长;ASSA反演中最佳模型参数和真值相差最大不到6.95% ,拟合差为30.17,反演时间相对适中。可以看出,综合考虑反演速度和拟合精度,自适应纯形模拟退火法相对于下降纯形法和模拟退火法具有一定的优越性。作者着重讨论自适应纯形模拟退火反演算法。 表2 对H型理论曲线反演结果 5.2 ASSA反演(加2%高斯噪声) 分析研究自适应纯形模拟退火法,我们对表1的2个三层模型和1个五层模型的正演响应(视电阻率和相位)分别加入2%的高斯噪声后再反演。H、K、HKH模型分别经过11 189、10 164、10 506次迭代,最终的拟合差依次为:30.17、36.19、32.74。反演结果如表3所示,反演模型基本反映了真实模型结构,最佳模型参数和真值相差最大不到13%。从表3可以看出,对于三层模型,反演后结果显示,K型的中间层分辨率不是很高,H型模型反演结果与真实模型基本吻合。五层模型的反演结果显示第三层的深度和电阻率反演效果相对略差,但基本反映出该高阻异常体,反演结果显示出地电结构的变化。图2(a) ~图2(c)分别对应H、K、HKH型地层反演后模型响应和合成数据。从图2可以看出,反演后的响应曲线与合成数据拟合较好,阻抗相位的拟合度比视电阻率的拟合度略差。在反演中,为了检验该方法的全局性,我们采用了不同的随机初始模型,进行多次的反演计算,所有反演计算结果都收敛于同一模型的最优解,整个算法在计算机上的运行时间为60 s左右,时间很短,反演效率比较高。 表3 加入2%高斯噪声反演结果 5.3 ASSA反演(加5%高斯噪声) 对加入2%高斯噪声电磁数据的反演效果良好,我们将噪声干扰增加到5%的高斯误差。H、K、HKH模型分别经过9 514、8 290、8 559次迭代,最终的拟合差依次为:37.52、43.81、40.49。反演模型参数如表4所示,反演模型参数值和真值相差不大,最佳模型参数和真值相差最大不到23%。图3(a)~图3(c)为合成数据曲线与反演的响应曲线的拟合对比图,拟合效果相对于加2%高斯噪声的情况略差,但整体的数据变化趋势基本一致。对于K型 图2 合成曲线(加2% 高斯噪声)与反演的响应曲线对比图Fig.2 Synthetic(2% gaussian noise) and inversion responses(a)H型;(b)K型;(c)HKH型 参数ρ1ρ2ρ3ρ4ρ5h1h2h3h4搜索范围[11000][11000][11000][11000][11000][110000][110000][110000][110000]H型107.0710.499.01//1014.883897.84//K型21.05103.5220.41//1045.654573.40//HKH型253.1722.1093.4611.2826.67614.911087.214033.855875.55 模型的中间频率段拟合相对于低频和高频段比较差,不过电性结构还是很清楚的体现出来了;对于HKH型模型,低频部分(深部)的拟合情况相对比较差,其原因为从地下深部返回的地电信息相对较弱,当观测资料含有与高频相同水平的噪声时,使得这些信息的信噪比大大降低,造成深部的反演结果变差。但是整体的拟合情况还是很好的,说明了该反演方法对于噪声有一定的抑制作用,所有的反演都基本搜索到了模型的全局最优解。此外,随着噪声的增加,收敛时拟合值增大,但是不影响该反演方法的全局收敛性。 图3 合成曲线(加5% 高斯噪声)与反演的响应曲线对比图Fig.3 Synthetic(5% gaussian noise) and inversion responses(a)H型;(b)K型;(c)HKH型 作者采用了模拟退火法和下降纯形法的非线性综合优化方法,综合二者的优点,实现快速有效地搜索全局最优解。为了减小大地电磁测深反演的多解性和提高分辨率,进行了视电阻率和阻抗相位的同时反演。 首先对比了下降纯形法、模拟退火法和自适应纯形模拟退火法,突出了自适应纯形模拟退火法的反演速度和拟合精度的优越性。然后采用自适应纯形模拟退火反演方法对三层H、K和五层HKH等模型进行了数值试验,检验了不同随机初始模型对反演结果的影响,我们对每个模型的合成数据进行多次的反演计算,所有的反演计算最终都收敛至同一最优解,不受初始模型选择的影响;加入2%高斯噪声的情况下,H型频段中间频段和HKH型的中间频段反演效果略差,其他各层电性结构得到较好的恢复;在加入5%高斯噪声的情况下,同样H型频段中间频段和HKH型的中间频段的反演结果相对较差,说明数据对这些结构反映不敏感,其它各层结构都得到较好的恢复。正演曲线和反演的响应曲线基本吻合,反演结果基本反映模型的地电结构变化。 数值试验过程中,反演后模型的分辨率随着噪声强度的增大都有所降低,其中H和HKH型的分辨率降低地比较明显,H型中频段和HKH型中频段的分辨率随着噪声的增强逐步降低,这是视电阻率和相位对中频段高阻层变化的不灵敏,这也是物理规律本身决定的。 这里所利用的反演方法是综合利用局部和全局最优的搜索方法,采用阻抗相位和视电阻率的同时反演,大大降低了解的非唯一性,提高了反演的精度和可靠性,是一种值得推广的混合优化算法,同时也为后续贝叶斯反演理论的研究奠定了良好的基础。 [1] 孙正江,王华俊.地电概论[M].北京:地震出版社,1984. SUN Z J,WANG H J. Overview of geoel- ectric[M].Beijing: Earthquake Press,1984.(In Chinese) [2] 柳建新.大地电磁测深法勘探-资料处理、反演与解释[M].北京:科学出版社,2011. LIU J X.Exploration of magnetotelluric sounding method[M].Beijing:Science Press,2011.(In Chinese) [3] 陈乐寿.大地电磁测深资料处理与解释[M].北京:石油工业出版社,1989. CHEN L S. Magnetotelluric sounding data processing and interpretation[M].Beijing: Oil industry Press,1989. (In Chinese) [4] 王家映.地球物理反演理论[M].北京:高教出版社,2007. WANG J Y.Geophysical inversion theory [M]. Beijing:HighereducationPress,2007.(In Chinese) [5] 刘云峰,曹春蕾.一维大地电磁测深的遗传算法反演[J].浙江大学学报,1997,31(3):300-305. LIU Y F,CAO C L. Genetic algorithm inversion of one-dimensional magnetote- lluric sounding[J].Journal of zhejiang university.1997,31(3):300-305. (In Chinese) [6] 杨文釆.非线性地球物理反演方法回顾 与展望[J].地球物理学进展,2001,17(2):255-261. YANG W C. Retrospect and prospect non-linear geophysical inversion methods[J]. Earth physics reviewed,2001,17(2): 255-261. (In Chinese) [7] 姚姚.蒙特卡洛非线性反演方法及应用[M].北京:冶金工业出版社,1997. YAO Y. The monte carlo nonlinear invers-ion method and its application[M].Beijing:Metallurgical industry Press,1997.(In Chinese) [8] KIRKPATRICK S,GELATT JR CD,VECCHI M P.Optimization by simulated annealing[J]. Science,1983,220:671-680. [9] METROPOLIS N,ROSENBLUTH A,R OSENBLUTH M,et.al. Equation of state calculations by fast computing machines[J].J .Chem Phys,1953,21:1087-1092 . [10]KIR KPATRICK S,CELATTCD,VECCHI M P.Optimization by simulated annealing[J].Sciences,1983,220:671-680. [11]ROTHMAN D H .Nonlinear inversion,stati-stical mechanics,and residual statics esti-mation[J]. Geophysics,1985,50(12):2784 -2796. [12]ROTHMAN DH.Automatic estimation of large residual statics correction[J]. Geop-hysics ,1986,51(2):337-346. [13]SEN M K , STOFFA P L .Nonlinear one-dimensional seismic wave form inversion using simulated annealing[J].Geophysics,1991,56(10):1624-1638. [14]SEND M K ,BHATTACHARYA B B,STOFFA P L. Nonlinear inversion of resistivity sounding data[J]. Geophysics, 1993,58(4): 496-507 . [15]师学明,王家映.一维层状介质大地电磁模拟退火反演法[J].地球科学-中国地质大学学报,1998,23(5):543-545. SHI X M,WANG J Y. one-dimensional layered media magnetotelluric simulated annealing inversion method[J]. Journal of China university of geosciences,1998,23(5): 543-545. (In Chinese) [16]于鹏,王家林,吴健生,等.重力与地震资料的模拟退火约束联合反演[J].地球物理学报, 2007, 50(2):529-538. YU P,WANG J L,WU J S,et,al. Gravity and simulated annealing constrained joint inversion of seismic data[J]. J. geophys,2007, 50(2):529-538. (In Chinese) [17]刘鹏程,纪晨.改进的模拟退火法-单纯形综合反演方法[J].地球物理学,1995, 38(2): 199-205. LIU P C.JI C. Improved simulated annea-ling method and simplex inversion meth-od[J].Geophys,1995,38(2):199-205. (InChinese) [18]HOLLAND,J.H.Adaptation in natural and artificial systems[M].University of Michigan Press,Ann Horbor, Michigan,1975. [19]PRESS, W. H., TEUKOLSKY, S.A..Simulated annealing optimization over continuous spaces[J]. Comput Phys, 1991(5): 426-450. [20]NELDER, J. A., MEAD, R. A simplex method for function minimization[J]. computer Journal,1965(7):308-313. [21]DOSSO SE,WILMUT M J,LAPINSKI A L S.An adaptive-hybrid algorithm for geoacoustic inversion[J]. IEEE Journal of Oceanic Engineering,2001, 26(3): 324-336. [22]刘文劼.频率和空间相关性观测数据条件下的大地电磁贝叶斯反演[D].长沙:中南大学.2012. LIU W J. Frequency and spatial correla-tion under the condition of the earth obs-ervation data and electromagnetic bayesi-an inversion[D]. Changsha:Central south university,2012. (In Chinese) [23]康立山.非数值并行算法(第一册)模拟 退火算法[M].北京:科学出版社,1997. KANG L S. Numerical parallel algorithm of simulated annealing algorithm[M]. Beijing: Science Press,1997. (In Chinese) [24]师学明,王家映.一维层状介质大地电磁模拟退火反演法[J].地球科学-中国地质大学学报,1998,23(5):543-545. SHI X M,WANG J Y. One-dimensional layered media magnetotelluric simulated annealing inversion method[J].Journal of China university of geosciences,1998, 23(5):543-545. (In Chinese) [25]师学明,王家映.地球物理资料非线性反演方法讲座(三)模拟退火法[J].工程地球物理学报,2007,4(3):165-174. SHI X M,WANG J Y. Geophysical data nonlinear inversion method lecture - the simulated annealing method[J].Journal of engineering geophysics,2007, 4(3): 165-174. (In Chinese) [26]郭荣文.贝叶斯MT反演的非线性和不确定度分析[D].长沙:中南大学, 2011. GUO R W. Bayesian MT inversion of the nonlinear and uncertainty analysis[D].Chang sha:Central south university,2011. (In Chinese) [27]范鸣玉,张莹. 最优化技术基础[M].北京:清华大学出版社,1982. FAN M Y,ZHANG Y. Optimization technology base[M].Beijing: Tsinghua university Press,1982. [28]席自强.单纯形-模拟退火法[J].湖北工学院学报,2000,15(1):27-29. XI Z Q. Simplex simulated annealing method[J].Journal of hubei institute of technology,2000,15(1):27-29.(In Chinese) [29]刘丽,苏敏. 基于改进模拟退火算法的医学图像配准[J].计算机应用及软件, 2008,25(5):223-259. LIU L,SU M. Based on improved simu-lated annealing algorithm of medical imageregistration[J].Computer applicat-ions and software,2008,25(5):223-259.(In Chinese) [30]曹治国,汪勇.基于模拟退火-单纯形法的目标函数的优化[J].华中科技大学学报: 自然科学版, 2005,33(6):67-68. CAO Z G,WANG Y. Based on simulated annealing, the objective function of opti-mization of simplex method [J] .Journal of huazhong universityof science and technology,2005,33(6):67-68. (In Chinese) One dimensional magnetotelluric sounding apparent resistivity and phase inversion of adaptive simplex simulated annealing study SUN Huan-le1a,b, WANG Shi-biao2, GUO Rong-wen1a,b,ZHOU Shao-min1a,b, LIU Jian-xin1a,b* (1.Central South University a.School of Geosciences and Info-Physics, b.Key Laboratory of Non-ferrous Resources and Geological Detection,Ministry of Hunan province,Changsha 410083,China; 2.Guang Dong Nonferrous Metals Engineering Investigation Design Institute,Guangzhou 510080,China) In order to avoid the linear inversion of MT falling into local extremum,and slow convergence rate of global optimization method, the authors adopt a comprehensive optimization method of adaptive simplex simulated annealing to the inversion of MT.On the one hand,this method could combine the advantages of both downhill simplex and simulate anneal arithmetic,which is proved to be a good way with global search capability and high-speed convergence.On the other hand, it achieved the simultaneously inversion of apparent resistivity and phase, which leads to the result of reducing the multi solutions and increasing resolution. Through numerical calculation of H,K and HKH models,this method shows high search efficiency and global convergence of comprehensive optimization method.The structure characteristics of real model could be reflected by inversion result of all the model synthetic data.As for some intermediate layers are relative high resistance models,the structures still could recover after inversion even if they are relative bad to other layers. magnetotelluric; apparent resistivity; phase; downhill simplex; simulated annealing; adaptive simplex simulated annealing 2015-08-11 改回日期:2015-09-24 国家科技基础专项(2013FY110800);国家自然科学基金(41174103);青年自科基金(41204081) 孙欢乐(1990-),男,硕士,从事电磁法正反演研究与应用, E-mail:miaomis@163.com。 *通信作者:柳建新(1962-),男,教授,博士生导师,从事电磁法理论与应用研究,E-mail:ljx6666@126.com。 1001-1749(2016)05-0584-09 P 631.4 A 10.3969/j.issn.1001-1749.2016.05.023 下降纯形法
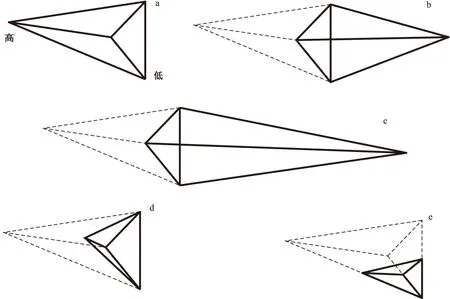
4 自适应纯形模拟退火法
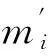
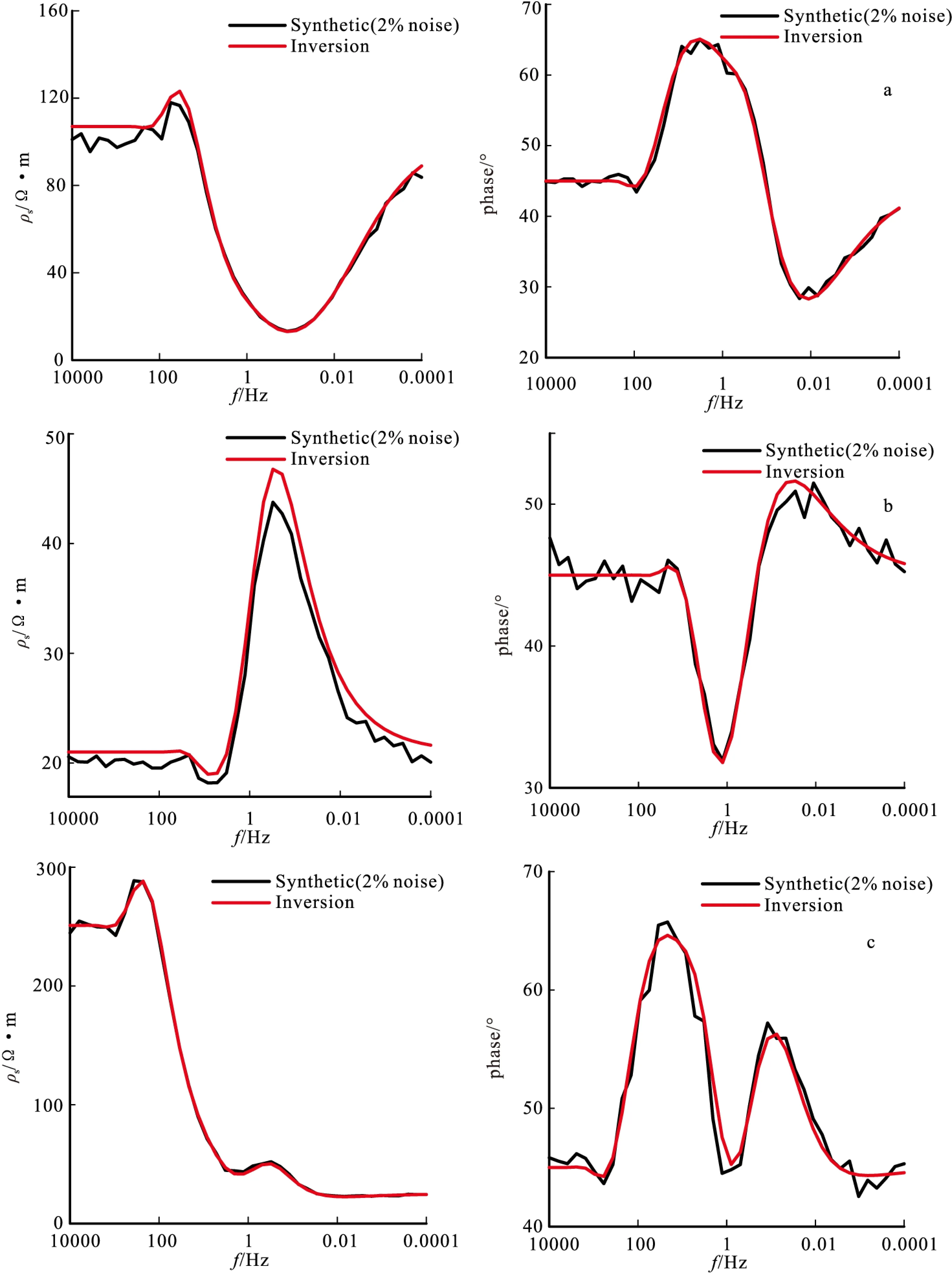
5 数值模拟计算实例




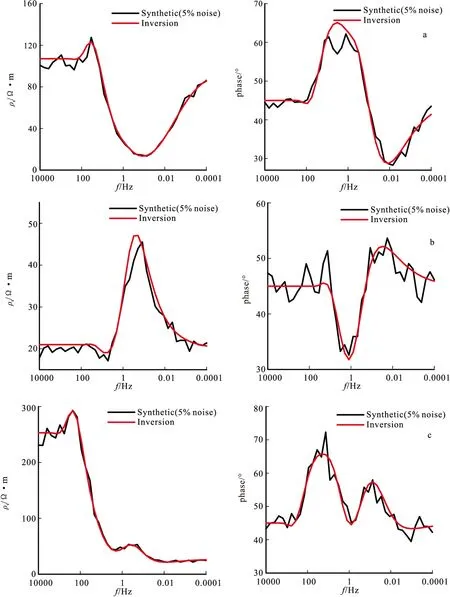
6 结论

