余热锅炉单相受热面动态建模与模型参数优化
李金波,程林
余热锅炉单相受热面动态建模与模型参数优化
李金波,程林
(山东大学热科学与工程研究中心,山东济南 250061)
作为余热利用环节中最重要的部分,余热锅炉的启动、变工况运行和停机特性直接决定锅炉的寿命及效率。基于工质热力学性质和质量、动量及能量守恒方程,以Matlab/Simulink为平台,构建了余热锅炉单相受热面的动态仿真模型。结合某水泥厂自主设计的直流余热锅炉实验数据,基于遗传算法和粒子群算法,对动态模型进行了参数优化。结果表明,经过优化后,余热锅炉动态模型与实验数据匹配程度高,模拟与实验结果的误差为0.93%~4.39%。因此,本文所建立的单相受热面变工况动态模型可以准确反映余热锅炉受热面动态特性。两种算法的对比表明,粒子群算法适应度函数收敛更优;在收敛迭代次数上,粒子群算法在54~64代达到收敛,遗传算法在93代后达到收敛。粒子群算法在参数优化方面优于遗传算法。
动态仿真;参数优化;实验验证;粒子群算法;遗传算法
引 言
能源问题一直是困扰社会发展的严峻问题。能源回收已成为能源行业最为关注的焦点。当今社会,高品质余热回收技术已经相当先进,而低品质余热回收问题仍旧需要进一步优化和解决。余热锅炉是低品质热源回收中最重要的部件,因此余热锅炉运行的分析和优化也成为众多余热产生行业研究的重点[1]。同时,随着余热锅炉结构系统的复杂化及工况的多变性,研究其动态特性及瞬态工况对余热锅炉的安全运行具有重要意义[2]。
在前人的研究中,对于余热锅炉变工况的研究主要分为数值计算与动态仿真。在数值计算研究方面Ray等[3]基于Shang[4]的超临界直流余热锅炉动态模型,构建了亚临界直流锅炉动态热工水力模型方程,并通过方程离散及电厂实验数据计算和对比不同工况不同受热面的运行情况。Rovira等[5]针对超临界压力下的锅炉,列举并求解了一维数学模型,同时以此模型为基础求解了部分负荷和满负荷时锅炉温度变化。张学镭等[6]以单压余热锅炉汽水系统为例,建立余热锅炉过热器、蒸发器和省煤器设计工况和变工况数学模型,通过编程求解计算模型方程,模拟锅炉汽水温度变化,并分析余热锅炉效率的影响因素。国内外学者基于不同的软件工作环境对余热锅炉整体及受热面进行过动态仿真。Alobaid等[7-8]利用相同的数据基于Advanced Process Simulation Software(APROS)和Advanced System for Process Engineering(ASPEN)软件对联合循环电厂余热锅炉启动过程的动态与静态建立仿真模型,并将结果进行对比。高建强等[9]基于一体化模型开发平台(IMMS),采用集总参数法建立了三压再热余热锅炉中单相工质受热管的动态数学模型,并开发了通用化的仿真算法及工程模块化的仿真模型。Benato等[10]分别基于Dynamic Modeling Laboratory(DYMOLA)商业建模软件和Matlab/Simulink对联合循环电厂整体进行动态建模和仿真,并对比分析了两种仿真方法所得结果的区别。
相关研究多数是仅基于余热锅炉受热面数学方程进行动态仿真,或是结合实验工况对数学方程进行调节。但是仍然存在一些问题,例如,模型仅局限于联合循环电厂的余热锅炉,数学方程简化程度较大,动态模型的准确性较低及模型对变工况下锅炉运行模拟适应度较低。
水泥行业是一个高能耗、高污染的行业。在典型水泥生产过程中,用于熟料冷却的篦冷机出口热风温度一般为200~500℃,余热品质低,温度波动大[11]。以该种热风作为热源,余热锅炉的动态特性需要得到准确的分析和不同工况预测,以保证锅炉的安全运行。同时由于水泥回转窑工况不稳定性,余热锅炉启停次数较多,因此分析余热锅炉受热面启停的动态特性尤为重要。
Matlab/Simulink是一款功能强大的动态仿真软件,计算效率高,速度快。其优势是在基于非线性方程构建动态模型的基础上,通过其嵌入的遗传、粒子群等优化算法,对方程中的参数进行优化,使模拟结果尽可能与实验相匹。
本文基于工质热力学性质及质量、动量和能量的数学方程,在Matlab/Simulink环境下,构建余热锅炉单相受热面动态数学模型,模拟瞬态工况。利用遗传算法和粒子群算法对模型参数进行优化,并与余热锅炉的实验结果相对比,建立了更准确的数学模型。基于两种优化算法所得数学模型,本文分析了余热锅炉单相受热面启停及变工况运行基本特性。
1 余热锅炉实验简介
根据某水泥厂余热的基本特征,本课题组设计并安装了U形立式直流余热锅炉。余热锅炉由8级受热面构成,分别命名为蒸发器1~3和省煤器4~8。各个受热面内布置有38 mm蛇形管管屏。烟气由蒸发器1上部入口竖直向下进入;经过省煤器4和底部灰斗后热风方向改为竖直向上;经过后4级受热面后从省煤器8上部出口排出,再经由除尘器进行尾气处理后排放到大气中。U形直流余热锅炉实验现场及余热发电系统结构如图1所示。
实验系统由容积为32 m3的圆柱型水箱供水,由两台额定流量32 m3·h−1的立式离心水泵提供循环动力,通过阀门控制水流量。给水加压后进入余热锅炉省煤器,经过受热面加热从蒸发器出口流出,进入挡板式汽水分离器进行蒸汽和饱和水的分离。随后汽、水分别由蒸汽管路进入汽轮机低压缸做功,及由回水管路返回水箱,进行新一轮的循环实验。
为测量不同工况下余热锅炉换热及蒸汽产量变化,在每个受热面的上下部位分别布置有6个热电阻,测量烟气、给水及蒸汽温度变化。为保证温度测量准确性,取平均值作为实验温度。在余热锅炉给水入口处安装涡轮流量计,汽水分离器出口蒸汽段安装涡街流量计,分别测量余热锅炉给水及蒸汽量。实验仪器详细参数见表1。
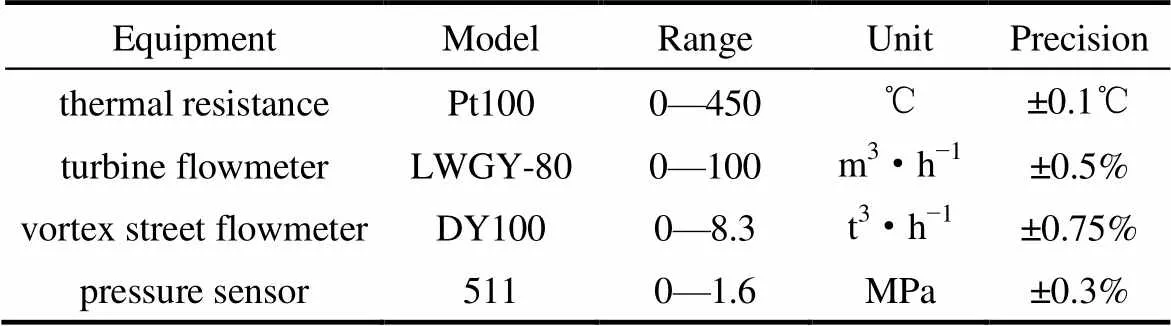
表1 实验仪器型号、量程及精度
为模拟余热锅炉不同单相受热面模型启动、停机及变工况运行,本文选取4种工况实验数据对模型进行参数优化与验证,具体实验工况参数见表2。其中Case 1为省煤器4受热面高温、高流量烟气工况,用于模型参数优化。Case 2为相同受热面不同工况的数据,验证模型及优化参数。Case 3和Case 4分别为省煤器5受热面低温、低流量烟气工况下用于参数优化和模型验证的实验数据。

表2 受热面模型进口参数
结合Case 1和Case 3数据,高、低温烟气工况下,受热面入口烟气、给水温度数据随时间变化如图2、图3所示。
2 单相受热面动态模型建立
根据余热锅炉主要受热部件换热管内工质状态,其分为单相受热面和两相受热面。省煤器、过热器为单相受热面。对于实验研究余热锅炉单相受热面,其整体尺寸2.5 m×2.5 m×2.5 m。换热管顺列布置,受热面由48件38 mm×3.5 mm蛇形管管屏和两联箱构成,结构如图4所示[12]。
单相受热面模型质量、动量、能量守恒方程及金属管壁热平衡方程如下[13-14]。
2.1 质量守恒方程
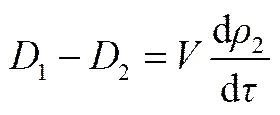
式中,1和2分别为单相受热面入口和出口工质流量;为受热面换热管容积;2为出口工质密度。
2.2 工质侧能量平衡方程
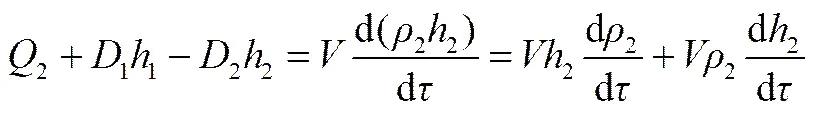
式中,2为整个区域管壁金属向管内介质传热量;1及2为换热管进出口工质焓值。
(3)
在省煤器中,水为不可压缩流体,根据实验数据,其压力可以认为恒定,动量方程可忽略。式(3)中,d2/d2=c2,c2为出口工质比定压热容。联立式(1)~式(3)得出口工质温度变化如式(4)所示
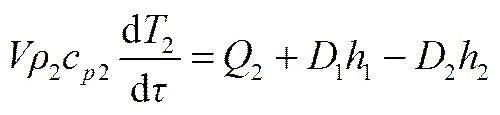
2.3 烟气侧能量平衡方程
(5)
式中,g、g及cg分别为烟气侧容积、烟气密度和比热容。以水泥窑低温余热锅炉流体成分为依据,热源为篦冷机冷却熟料所得热空气,所以气相可视为空气介质进行计算[15-16]。g1及g2分别为受热面烟气进出口温度。g为烟气流量,为保热系数,其值根据余热锅炉受热面实际结构决定。
2.4 传热方程
根据实验测得,余热锅炉入口烟气温度变化范围为250~300℃,省煤器入口烟气温度变化范围为150~200℃。因此仅考虑烟气、换热管壁与工质之间的对流换热,忽略辐射换热。
烟气侧换热基本方程为
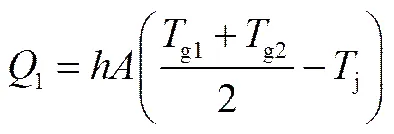
式中,为受热面对流传热系数;为受热面总换热面积;j为金属管壁温度。烟气在过热器、再热器、省煤器等单相受热面中,横向冲刷换热管,对于顺列管束,根据Zhukauskas公式可得[17-18]
(7)
其中
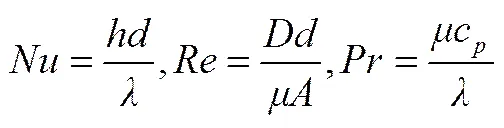
式中,为换热管内径;为工质热导率;为工质动力黏度;z为沿烟气流向的管排数的修正系数,当管排数大于10时,z=1.0;s为换热管修正系数,其值与管排横向、纵向间距有关。因此式(7)化简得
(8)
烟气与金属管壁的对流换热方程如式(9)
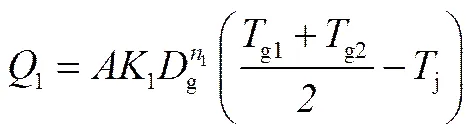
给水在单相受热面中,纵向冲刷换热管,对于顺列管束,根据Dittus-Boelter公式,换热基本方程及计算公式如下[17-18]
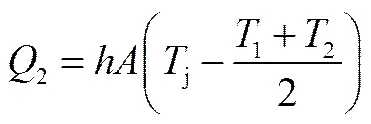
(11)
则对流传热系数表达式如下
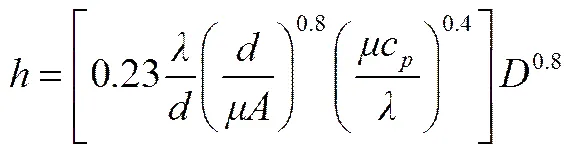
由此可得,金属管壁与介质的对流换热方程如下
(13)
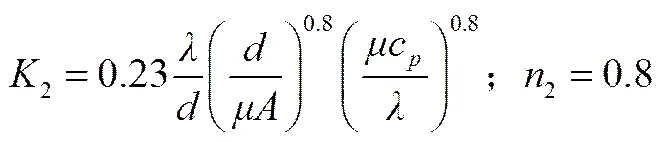
其中,1及2为倍率系数。
2.5 金属蓄热方程
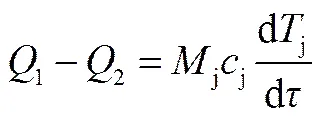
式中,j、j分别为区段内金属总质量及金属比热容。由式(6)~式(14)联立可得金属管壁温度变化式。
以上各个符号的取值见表3。

表3 模型物理量参数
3 模型仿真与参数优化方法
3.1 模型的Matlab/Simulink仿真
基于上文中简化得到的烟气、金属及给水温度变化微分方程,余热锅炉单相受热面动态模型由Matlab/Simulink软件模拟,图5为对应的Simulink框图。在图5所示模型中,由上到下可分为3部分,分别对应给水吸热、烟气放热及金属蓄热方程。其中水的热力性质函数是基于IF97标准并嵌入Simulink框图中;烟气密度与比热容性质函数由实验数据拟合为方程并嵌入Simulink模型[19]。由于微分方程考虑了受热面金属换热管蓄热,模型可以更好反映出烟气、给水与金属管壁之间的温差变化情况,避免了将金属管壁与给水等效为同样温度进行计算的假设所造成的误差。根据实验数据,在任何工况下,金属管壁的温度应低于该位置烟气的温度,同时高于给水温度。出口烟气、给水温度初始值根据不同工况下实验温度进行设定,根据不同模拟需求和实验数据设定模拟时间和工况。本文模拟工况分别为:冷启动-稳定;冷启动-稳定-停机;冷启动-变工况-停机。
3.2 模型参数优化
由前介绍,在单相受热面的微分方程中保热系数,倍率系数1及2均由受热面结构决定。因此其取值影响动态仿真模型与实验数据的契合精度,需要对其取值进行优化以达到模型与实验结果相一致的要求。Holland[20]设计的遗传算法是一种非常适合此种计算的方法。基于达尔文适者生存的生物理论,对于不同的工程优化及非线性问题,遗传算法优势明显,更多的介绍见文献[21-22]。结合余热锅炉受热面实验结果,适应度函数为烟气和工质实验值与误差值的二阶范数,如式(9)所示
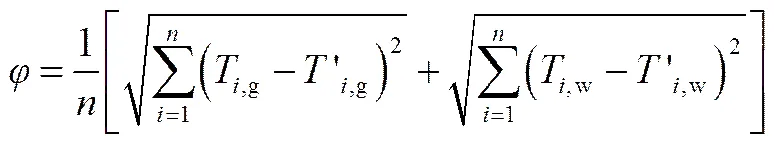
式中,T,g、′,g分别为相同时刻下受热面烟气出口温度模拟值与实验值;T,w′,w分别为相同时刻下受热面工质出口温度模拟值与实验值。适应度函数最小值所对应的、1及2,表示在整个模拟过程中,模拟值与实验值吻合程度最高,模型参数准确度最高。
为对比优化算法的模拟结果,同时使用粒子群算法(PSO)对受热面动态仿真模型进行优化。粒子群算法由Kennedy等[23]于1995年提出。其理论基础是昆虫群居的社会行为,是基于多代迭代的优化算法。在同一代中,每个个体在搜索空间中有一个位置和速度,在每次迭代后更新。同时在算法中,还使用了一些控制参数的更新速度和位置的方法,以避免局部极小。粒子的速度和位置求解公式如下所示[24-25]
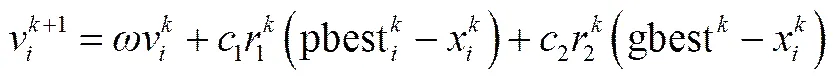
(17)
式中,v 、x分别为第步计算过程中第颗粒的速度和位置;pbest为第步计算结果中颗粒最优值,gbest为整个计算过程中颗粒最优值。、、分别为控制参数,其中为惯性权重;为在第步从0到1的随机数;为学习因子。表4为遗传算法和粒子群算法相关参数选择。图6为遗传算法及粒子群算法优化流程。
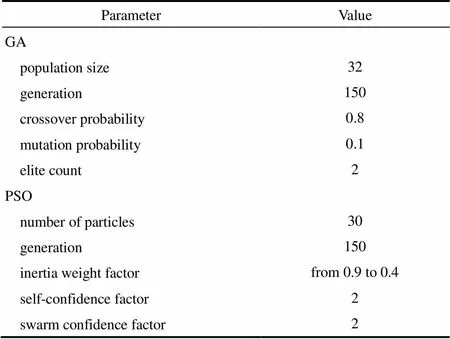
表4 遗传算法与粒子群算法优化参数的设定
由于实验数据是离散的过程,模拟数据则是在整个时间段内的连续过程,因此在基于优化算法得到结果后根据实验时间对模拟结果进行插值计算,得到与实验数据相同时刻的模拟结果。在优化过程中变量的变化是一个随机过程,但每个变量均存在各自的合理范围。这些范围的求解是基于模型运行符合实际的条件。在余热锅炉受热面中,烟气加热给水,因此热量应保证从烟气传导至给水。为满足上述条件,变量范围及限制条件如下
80%<<100%
0<1<0.015
0<2<5
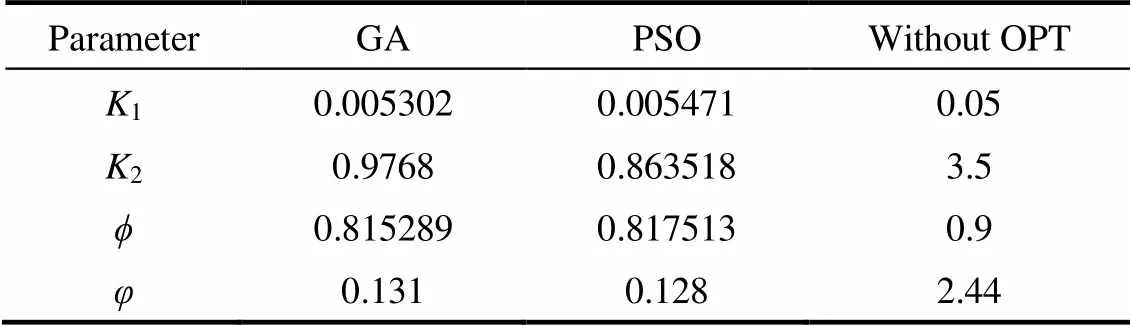
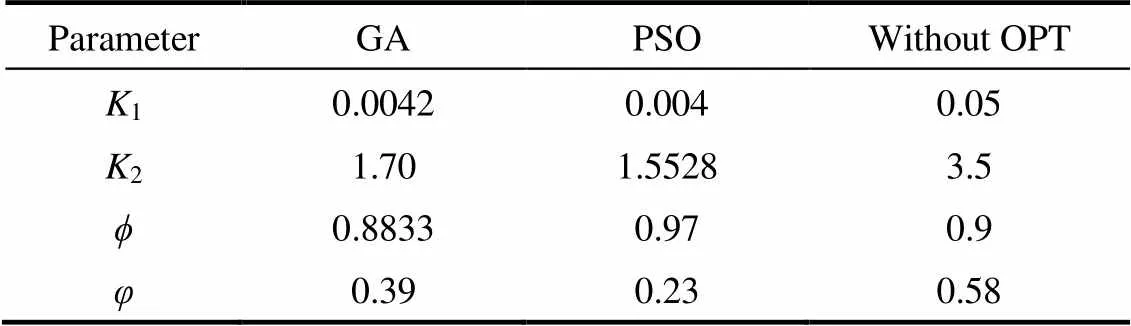
1 1范围选择是基于式(5)、式(9),满足 2取值范围是基于式(9)、式(13),满足 (19) 分析了烟气流量(标况下)17000~32000 m3·h-1,给水流量3~15 t·h-1多种工况下余热锅炉省煤器4和5受热面冷启动、停机及变工况运行的过程。入口烟气温度及水温采用余热锅炉实验温度,并将优化后出口温度与各个工况下实验数据进行对比分析。优化后模型与实验结果更为吻合,准确度更高,具体结果及分析如下。 4.1 Case 1受热面省煤器4参数优化及对比 由表5、图7(OPT-算法优化;EXP-实验研究)启动段动态仿真优化结果可得,采用遗传算法和粒子群算法对Matlab/Simulink模型进行优化后,余热锅炉动态模型与实验数据匹配程度高,模型与实验的平均误差为0.93%~4.39%。因此,可以用该模型参数模拟余热锅炉受热面冷启动过程。同时,在冷启动过程中水温变化与烟气温度变化具有相同的增加趋势,但是水温变化相对于烟气温度变化具有一定的延迟,具体体现在烟气温度变化曲线斜率大于给水温度变化斜率。 表5 省煤器4受热面优化前后参数对比 遗传算法和粒子群算法优化速度及收敛值如图8所示。由适应度函数收敛过程可得,两种优化方法适应度函数收敛值近似,偏差2.29%,粒子群算法收敛值0.128;在收敛迭代次数上粒子群算法在54~64代达到收敛,遗传算法在93后代达到收敛。因此,在Simulink动态仿真模型算法优化过程中,遗传算法优化收敛较为缓慢。 4.2 Case 2受热面省煤器4优化参数实验验证 针对于Case 1省煤器4受热面优化参数,选取该受热面其他工况下实验结果进行检验,验证优化参数的普遍性,结果如图9所示。由图可得,采用Case 1所得优化参数在相同受热面其他工况的模拟中同样有效,模型可以较好反映出实验工况下受热面冷启动的过程。 4.3 Case 3受热面省煤器5参数优化及对比 采用同样方法对该余热锅炉省煤器5受热面进行建模与优化,具体参数及结果如表6和图10所示。 由图可得,模型优化后可以较好反映余热锅炉的受热面启停过程。对比该余热锅炉启动和停机时间,停机时间约为启动时间的2倍。停机过程温度变化呈现先迅速下降、后缓慢下降的过程。在余热锅炉停机所导致的降温过程中,给水延迟性尤为明显,出口烟气低于出口给水,但最终烟气与给水温度降至近似相同的温度,逐渐冷却至环境温度。 表6 省煤器5受热面优化前后参数对比 4.4 Case 4受热面省煤器5优化参数实验验证 Case 4选择相同受热面,不同工况下的实验结果,作为Case 3的验证,同时对该模型进行受热面变工况运行的模拟,其结果如图11所示。 Case 1~Case 4 分别对应高温工况余热锅炉启动、低温工况余热锅炉启动与停机以及变工况运行。对比以上4种工况可得,余热锅炉单相受热面启动过程与所需时间近似,即启动过程所需时间与烟气量、烟气温度相关性小;通过对比Case 1和Case 3的优化结果可知,省煤器4受热面保热系数较低,说明在运行过程中,烟气热量较多散至空气中去,因此应对其增强保温措施。 基于工质热力学性质及质量、动量、能量守恒方程建立了余热锅炉单相受热面Matlab/Simulink动态仿真模型。主要结论如下。 (1)结合余热锅炉单相受热面的实验数据,采用遗传算法和粒子群算法对动态仿真模型进行参数优化,确定受热面守恒方程中相关参数。经过算法优化后,余热锅炉动态仿真模型与实验结果更加吻合,仿真模型可用于预测不同工况下余热锅炉的实际性能。两种优化方法适应度函数收敛值近似,偏差2.29%。PSO算法收敛值更低,收敛时间更短,在余热锅炉参数优化方面,其优于GA算法。 (2)余热锅炉停机时间约为启动时间的2倍。停机过程温度变化先迅速下降,后缓慢下降。在冷启动与停机过程中水温变化呈现与烟气温度变化相同的趋势,但相对于烟气温度变化具有一定延迟。 (3)单相受热面启动过程所需时间与烟气量、烟气温度相关性小;省煤器4受热面保热系数较低,因此应对其增强保温措施。 A——受热面总换热面积,m2 cj——金属比热容,kJ·kg−1·K−1 cpg——烟气比热容,kJ·kg−1·K−1 cp2——出口工质比定压热容,kJ·kg−1·K−1 Dg——余热锅炉烟气流量,m3·h−1 D1, D2——分别为余热锅炉受热面进、出口给水流量,m3·h−1 h——受热面对流传热系数,W·m−2·K−1 h1, h2——分别为换热管进、出口工质焓值,kJ·kg−1 K1, K2——倍率系数 Mj——金属质量,kg n1, n2——补偿系数 Q2——管壁金属向管内介质传热量,kW Tg1, Tg2——分别为受热面进、出口烟气温度,℃ Tj——金属管壁温度,℃ T1, T2——分别为受热面进、出口给水温度,℃ V——单相受热面换热管容积,m3 Vg——烟气侧容积,m3 λ——工质热导率, W·m−1·K−1 ρg——烟气密度,kg·m−3 ρ2——出口工质密度,kg·m−3 φ——适应度函数 ϕ——保热系数 [1] BEHBAHANI-NIA A, BAGHERI M, BAHRAMPOURY R. Optimization of fire tube heat recovery steam generators for cogeneration plants through genetic algorithm [J]. Applied Thermal Engineering, 2010, 30(16): 2378-2385. [2] SINDAREH-ESFAHANI P, HABIBI-SIYAHPOSH E, SAFFAR-AVVAL M,. Cold start-up condition model for heat recovery steam generators [J]. Applied Thermal Engineering, 2014, 65(1/2): 502-512. [3] RAY A, BOWMAN H F. A nonlinear dynamic model of a once-through subcritical steam generator [J]. Journal of Dynamic Systems MeasurementControl, 1976, 98(3): 332-339. [4] SHANG T L. A Dynamic Model of Once-Through Supercritical Pressure Boiler [M]. Saarbrücken: Juris-Verlag, 1971. [5] ROVIRA A, VALDES M, DURAN M A D. A model to predict the behavior at part load operation of once-through heat recovery steam generators working with water at supercritical pressure [J]. Applied Thermal Engineering, 2010, 30(13): 1652-1658. [6] 张学镭, 王松岭, 陈海平, 等. 非补燃余热锅炉变工况性能计算模型及分析[J]. 华北电力大学学报(自然科学版), 2010, 37(4): 53-58. ZHANG X L, WANG S L, CHEN H P,. Calculation and analysis model of off-design performance for heat recovery steam generator without supplementary firing [J]. Journal of North China Electric Power University, 2010, 37(4): 53-58. [7] ALOBAID F, STARKLOFF R, PFEIFFER S,. A comparative study of different dynamic process simulation codes for combined cycle power plants (Part A): Part loads and off-design operation [J]. Fuel, 2015, 153: 692-706. [8] ALOBAID F, STARKLOFF R, PFEIFFER S,. A comparative study of different dynamic process simulation codes for combined cycle power plants (Part B): Start-up procedure [J]. Fuel, 2015, 153: 707-716. [9] 高建强, 郝娜, 范晓颖, 等. 余热锅炉单相受热面动态数学模型及仿真[J]. 华北电力大学学报(自然科学版), 2009, 36(3): 68-71. GAO J Q, HAO N, FAN X Y,. Dynamic mathematical model and simulation for single-phase heat exchanger of heat recovery steam generator [J]. Journal of North China Electric Power University, 2009, 36(3): 68-71. [10] BENATO A, STOPPATO A, BRACCO S. Combined cycle power plants: a comparison between two different dynamic models to evaluate transient behaviour and residual life [J]. Energy ConversionManagement, 2014, 87: 1269-1280. [11] SUI X, ZHANG Y, SHAO S,. Exergetic life cycle assessment of cement production process with waste heat power generation [J]. Energy ConversionManagement, 2014, 88: 684-692. [12] 杜文静, 王沛丽, 程林. 一种新型受热面传热和流动特性的数值模拟及实验研究[J]. 化工学报, 2015, 66(6): 2070-2075. DU W J, WANG P L, CHENG L. Numerical simulation and experimental research on novel heat transfer surface [J]. CIESC Journal, 2015, 66(6): 2070-2075. [13] ALOBAID F, STROHLE J, EPPLE B,. Dynamic simulation of a supercritical once-through heat recovery steam generator during load changes and start-up procedures [J]. Hydrotechnical Construction, 2009, 86(7/8): 1274-1282. [14] SIIKONEN T. Numerical method for one-dimensional two-phase flow [J]. Numerical Heat Transfer Applications, 2007, 12(1): 1-18. [15] MANSOURI M T, AHMADI P, KAVIRI A G,. Exergetic and economic evaluation of the effect of HRSG configurations on the performance of combined cycle power plants [J]. Energy ConversionManagement, 2012, 58(3): 47-58. [16] AHMADI P, DINCER I. Thermodynamic analysis and thermoeconomic optimization of a dual pressure combined cycle power plant with a supplementary firing unit [J]. Energy ConversionManagement, 2011, 52(5): 2296-2308. [17] 杨世铭, 陶文铨. 传热学[M]. 2版. 北京: 高等教育出版社, 2006: 246-261. YANG S M, TAO W Q. Heat Transfer [M]. 2nd ed. Beijing: Higher Education Press, 2006: 246-261. [18] 郭喜燕. 火电机组动态过程性能在线监测研究[D]. 北京: 华北电力大学, 2004. GUO X Y. Transient process performance monitoring of coal-fired power generating unit [D]. Beijing: North China Electric Power University, 2004. [19] AMERI M, AHMADI P, KHANMOHAMMADI S. Exergy analysis of a 420 MW combined cycle power plant [J]. International Journal of Energy Research, 2008, 32(2): 175-183. [20] HOLLAND J H. Adaptation in Natural and Artificial Systems [M]. Cambridge: MIT Press, 2015: 126-137. [21] SIMON D. Evolutionary Optimization Algorithms [M]. Wiley, 2013. [22] SIVANANDAM S N, DEEPA S N. Introduction to Genetic Algorithms [M]. Cambridge: MIT Press, 1998: 293-315. [23] KENNEDY J, EBERHART R. Particle swarm optimization [C]// IEEE International Conference on Neural Networks. 4. Piscataway: IEEE Computer Society, 1995: 1942-1948. [24] SADEGHZADEH H, EHYAEI M A, ROSEN M A. Techno-economic optimization of a shell and tube heat exchanger by genetic and particle swarm algorithms [J]. Energy ConversionManagement, 2015, 93: 84-91. [25] VANDANI A M K, BIDI M, AHMADI F. Exergy analysis and evolutionary optimization of boiler blowdown heat recovery in steam power plants [J]. Energy ConversionManagement, 2015, 106: 1-9. Dynamic modeling and parameter optimization of single phase heating surface of heat recovery steam generator LI Jinbo, CHENG Lin (Center of Thermal Science and Technology, Shandong University, Jinan 250061, Shandong, China) Heat recovery steam generator (HRSG) is the most important part of the waste heat utilization, and the start-up, shutdown and off-design operation of the HRSG directly determines its life and efficiency. Based on the thermodynamic properties and mass, momentum and energy conservation equations, and taking Matlab/Simulink as the research platform, a dynamic simulation model of the single phase heat transfer surface of HRSG is built in this paper. Combined with the experimental data of the HRSG designed by research group in a cement plant, the parameter optimization of the dynamic model is carried out based on genetic algorithm and particle swarm optimization algorithm. The results show that after optimization, the dynamic model of the waste heat boiler is matched with the experimental data, and the error of the model is 0.93%—4.39%. The dynamic model can be used to simulate the temperature change of the heat transfer surface under different working conditions.And through the comparison of the two algorithms, it shows that particle swarm optimization algorithm has obvious advantages in parameter optimization. The fitness function convergence value is better, and in the convergence iteration, it finishes between the 54 and 64 generation. The genetic algorithm achieves convergence after the 93 generation. dynamic simulation; parameter optimization; experimental validation; particle swarm optimization; genetic algorithm 2016-05-27. Prof. CHENG Lin, cheng@sdu.edu.cn 10.11949/j.issn.0438-1157.20160721 TK 124 A 0438—1157(2016)11—4599—10 李金波(1989—),男,博士研究生。 国家重点基础研究发展计划项目(2013CB228305)。 2016-05-27收到初稿,2016-07-12收到修改稿。 联系人:程林。 supported by the National Basic Research Program of China (2013CB228305).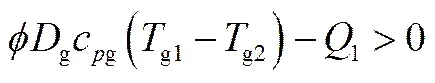
4 结果对比与讨论
5 结 论
符 号 说 明

References

