基于LabVIEW的振动信号分析系统设计
唐 奕,李 祺,王文娟,马云彤,刘 旺
(1.哈尔滨工业大学 自动化测试与控制系, 哈尔滨 150080;2.中国航天科工集团第三研究院 无人机技术研究所,北京 100074;3.北京机电工程研究所,北京 100074)
基于LabVIEW的振动信号分析系统设计
唐 奕1,李 祺2,王文娟3,马云彤1,刘 旺1
(1.哈尔滨工业大学 自动化测试与控制系, 哈尔滨 150080;2.中国航天科工集团第三研究院 无人机技术研究所,北京 100074;3.北京机电工程研究所,北京 100074)
针对机械故障监测的需求,开发了振动信号分析系统;采用LabVIEW图形化开发工具,系统实现了振动信号分析流程和基本的信号分析方法,能够对振动信号进行预处理,并从时域、频域和时频域角度对其进行特征提取;完成了基于仿真信号和实测的公开振动数据集的系统功能验证,采用希尔伯特-黄变换法对西储凯斯轴承的一组数据进行测试,结果表明,所开发的振动信号分析系统能够分辨出轴承故障的特征频率,相对误差为0.84%,同时具备参数配置灵活、结果显示直观、扩展性强的优势,为基于振动测试的机械故障监测提供了基础平台。
故障检测;振动测试;信号分析;LabVIEW
0 引言
随着工业化程度不断提高,复杂系统中使用的机械设备日趋智能化、复杂化和精密化[1],而机械设备的工作性能和运行状态直接影响复杂系统的整体运作。因此,机械设备的可靠性变得越来越重要,机械状态监测获得更多重视。
在设计、生产和运行各个阶段监测设备的状态有助于优化设计生产,运行中及时发现故障采取对策。机械设备及其零部件长时间连续运行在高温环境下,由于挤压、摩擦或冲击等原因会产生结构关系的变化,发出异常振动信号。对振动信号进行监测和分析就能在一定程度上获取设备的运行状态。现阶段针对振动分析提出了很多方法,小波法、Hilbert-Huang法[2-4]、阶次分析[5-7]、神经网络算法以及盲源分离[8-9]都在以振动测试为基础的机械故障监测领域有广泛应用。目前成熟的振动测试平台的开发设计多利用Visual Studio、C++和Matlab等工具,Visual Studio虽可设计可视化界面,但程序代码仍以C语言为基础,对技术人员程序设计要求较高,开发周期较长;Matlab具有强大的数据运算功能,但不能很好地实现数据采集和仪器控制。
振动测试基础平台应能实现振动测试的完整流程,具备数据采集、分析和仪器控制的能力,提供可配置的参数和清晰直观的结果显示。LabVIEW作为一种标准的数据采集和仪器控制软件[10],提供图形化程序设计平台以及高级信号处理工具包,方便对振动信号进行处理和分析。因此,振动信号分析系统主要采用LabVIEW工具进行开发。
1 振动测试流程
振动测试技术通过对机械设备发出的振动信号进行采集和分析判断设备的状态,是一种直观有效的机械设备状态监测方式,其基本流程包括4个步骤:信号采集、信号预处理、信号特征提取和故障诊断与决策,如图1所示。
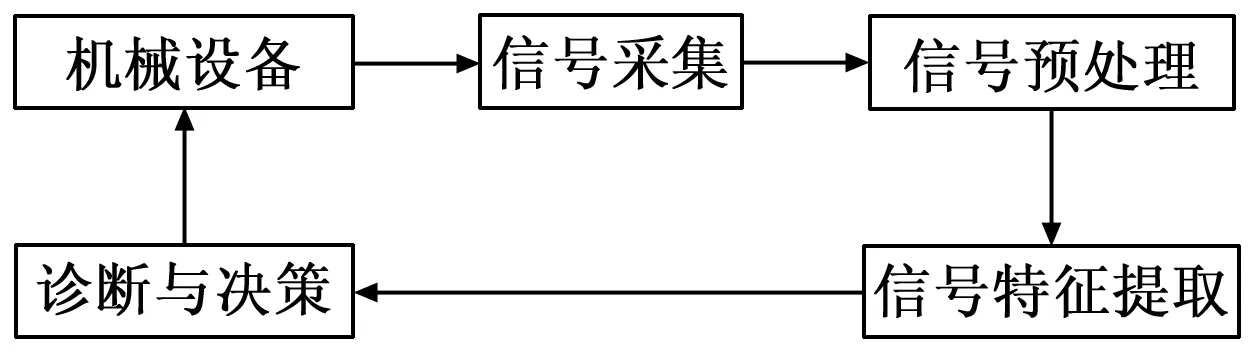
图1 振动测试流程图
1.1 信号采集
振动测试首先要获取设备的振动信号,在合理的位置安装传感器可以获取机械设备不同方向的振动数据。本文面向的测试数据利用仿真信号和开放的振动数据集产生,故系统设计信号源选择模块代替振动测试中的信号采集部分用以产生振动数据,并作为信号分析系统的输入。
1.2 预处理
传感器实时采集机械设备在工作环境中的振动数据,所得的原始信号不可避免的包含噪声干扰[11]。为保证可靠性,在对信号进行特征提取前需要将原始采集信号进行处理,在一定程度上滤除干扰[12]。本文设计信号预处理模块,实现去趋势项、数据平均、重采样和滤波功能。
1.2.1 去趋势项
趋势项主要由采集、数模转换设备中的放大器漂移引起,也由某些固定的环境因素持续作用于设备而产生趋势性误差[13],可分为线性趋势项和非线性趋势项。去趋势项的传统方法包括平均斜率法和最小二乘法,而现代又发展出基于小波变换、经验模态分解的去趋势项方法。本文基于设计基于最小二乘法和经验模态分解的去趋势项方法,实现去除线性和非线性趋势项的功能。
1.2.2 数据平均
数据平均用于剔除误差较大的异常数据,实现数据平滑和拟合。基本的数据平均方式为移动平均法。移动平均法以定长的数据窗沿时间轴滑动,同时对窗内数据加和取平均数。这种方法算法简单,但效果有限,在移动平均的基础上发展出了指数平均法。指数平均法对窗内数据进行加权操作,近期的数据权值越大,与移动平均相比具有更好的处理效果。本文设计了移动平均和指数平均方法实现数据平均。
1.2.3 重采样
传感器以一定采样率采集得到原始振动信号,在后续处理中根据信号特点和分析方法不同需要改变采样率即进行重采样,以求更有效的提取振动信号特征。重采样的思路有两种:一是改变采样间隔,即升降采样;二是改变采样方式,如阶次分析中用到的等角度采样。
等间隔升降采样可以放大或缩小信号的某种特征,而等角度采样主要针对变速过程中的采样。当机械设备匀速运行时故障率较低,而机械故障常发生在启停机或加减速过程中。在变速过程中如果仍采用等间隔采样则每采样一次机械变化的程度不同,不利于提取设备特征。而通过算法转换为等角度采样后,能保证每一段采样设备的加速情况相同,便于对设备特征进行提取。本文设计升降采样和基于等角度采样的阶次分析方法。
1.2.4 滤波
滤波可以从频率角度去除频率干扰,可分为传统滤波和现代滤波。传统滤波器通过改变滤波器拓扑结构、通阻带等参数实现滤波效果,而现代滤波器基于小波、经验模态分解等算法,对原始信号进行重构或分解,从而达到滤波效果。本文设计传统滤波器实现滤波功能。
经过预处理的信号在一定程度上去除了噪声干扰,可以较为准确地进行特征提取。
1.3 特征提取
振动信号中包含大量设备状态信息,对振动信号进行特征提取可以初步反映设备状态,为后续状态监测算法的学习和训练机制提供数据支持,为模式识别提供基础。振动信号普遍具有时域、频域和时频域3个分析角度的特征,本文设计特征提取模块对这3个方面的特征进行提取。
1.3.1 时域特征
采集到的信号多为时间信号,时域上包含了信号较多特征,观察分析最为直观。信号的时域分析分为时域统计分析和时域相关性分析。时域统计分析主要利用统计学知识对获取信号初步特征,时域相关性分析可以获取信号间的相关性。
1)时域统计分析:时域统计指标分为基本统计参量和无量纲参量。基本统计参量反应信号的基本时域信息,常用的有峰值、均方根和峭度。峰值和均方根分别反映振动数据最大振动幅度和整体振动情况,而峭度表征数据概率密度的尖峭程度,更常用来反应振动状态。无量纲参量主要包括峭度指标、波形指标、脉冲指标和峰值指标等。
2)相关性分析:相关性分析分为自相关分析和互相关分析。自相关反应同一信号不同时间点上数据间的相关程度,用来去除信号中耦合的随机噪声。互相关反应两组信号同一时间点上数据间的相关程度,用来对比两组相近的信号。
本文主要对时域统计指标中的参量进行测量,同时可以获取信号的自相关情况。
1.3.2 频域特征
信号的时域特征能在一定程度上反应机械设备的状态,但由于故障初期结构变化较小,不易在时域特征中体现出来,但细小的机械结构变化会在振动信号中产生新的频率成分,因此可以通过变换域分析方法从频域角度监测设备状态。常用的频域分析方法包括幅值谱分析、功率谱分析和倒频谱分析。
1)幅值谱:幅值谱体现振动幅度与频率分布的关系,从中可以获取主要振动频率分布,可以分辨机械设备的特征频率[14]。
2)功率谱:功率谱体现功率能量与频率分布的关系,可以揭示信号中隐含的周期性和邻近的频峰。功率谱可分为经典谱估计和现代谱估计,较为常用的方法是现代谱估计中的AR谱估计[14]。
本文实现信号频域幅度谱和功率谱计算和分析。
1.3.3 时频域特征
信号时域和频域分析存在各自的局限性,针对非平稳信号采用时频域分析方法,将一维时间尺度投射到二维的时间频率尺度上,在同一个平面上同时显示时域和频域的细微变化[15]。本文设计STFT和Hilbert-Huang法进行时频域分析。针对Hilbert-Huang法中的经验模态分解,本文进行分析方法优化,选取与原始信号相关性较大的本征模量进行进一步包络谱分析。
1.4 故障判断与决策
特征提取获取到的设备基本状态参数用于进一步学习训练和模式识别,能够及时发现和识别设备故障,采取相应措施。
复杂的数据学习训练和模式识别算法的基础是信号的获取、处理和特征提取,本文借助基本的振动分析方法搭建振动测试平台,实现信号的处理和特征提取功能。
以上完成了搭建振动测试系统的准备工作,下面对系统的实际振动信号分析系统软件实现进行介绍。
2 振动信号分析系统
本文借助LabVIEW工具的数据采集、分析及仪器控制功能,搭配Matlab强大的数据计算工具,设计振动信号分析系统。选定开发环境为LabVIEW2014及Matlab2012b。
2.1 系统总体框架
本系统整体框架利用LabVIEW中的状态机利用主从设计模式,搭配队列功能和簇函数实现按自定义顺序转换不同模块的功能,如图2所示。
按照振动信号分析系统功能划分,系统功能模块包括以下4个部分:信号预处理、信号特征提取、信号源选择和文件管理。其中预处理和特征提取两个模块对应于振动测试流程中的两个步骤,而信号源选择模块用于代替信号采集部分选取测试系统的信号输入,文件管理模块用于实现数据的存取功能。
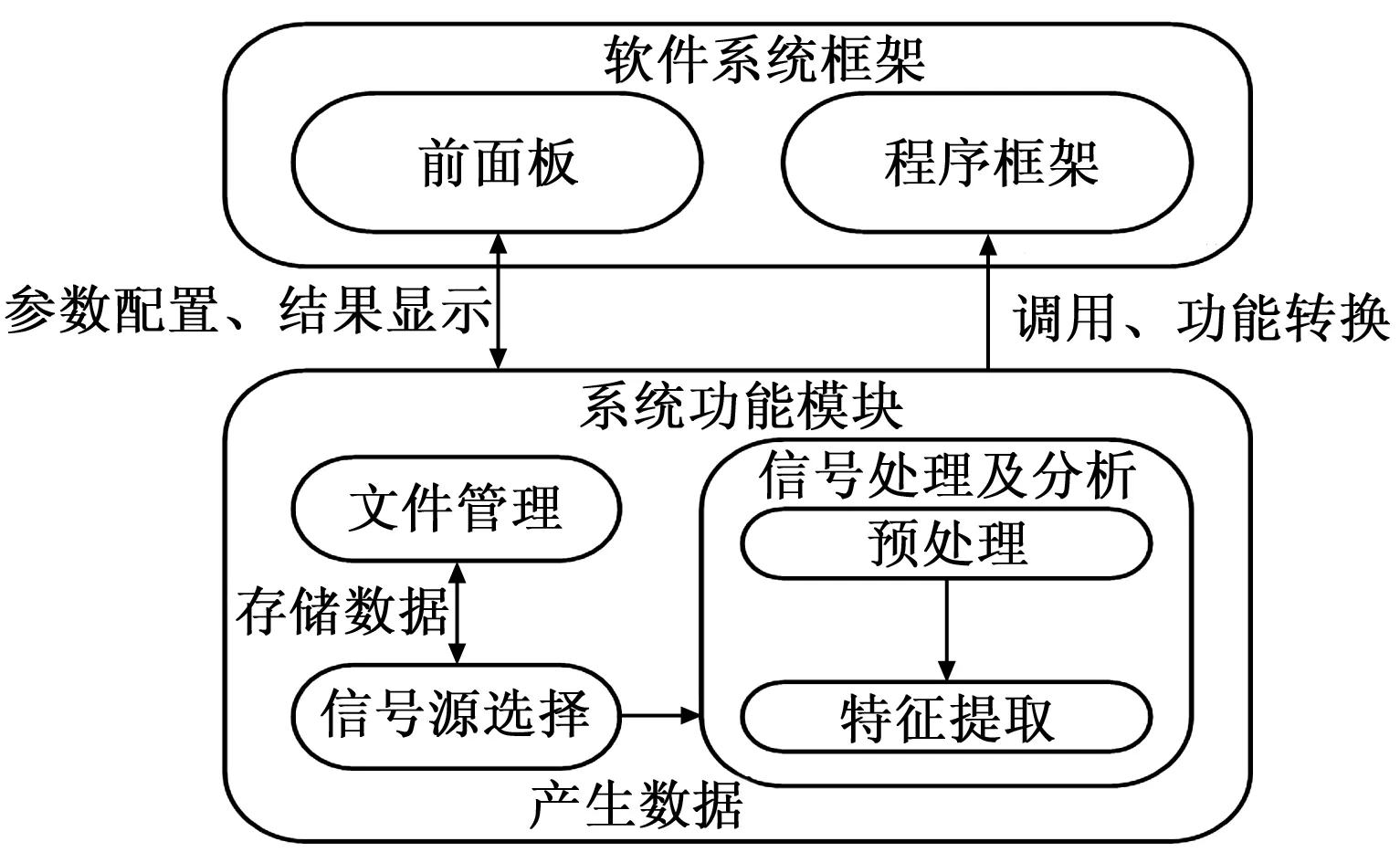
图2 软件系统框架
信号源产生原始数据作为系统输入,经过文件管理模块存储并选择需要分析的数据,之后数据依次经过信号预处理模块和信号特征提取模块进行信号处理和分析。以下按照振动测试中数据的流动顺序对系统的各模块进行介绍。
2.2 信号源选择模块
本文面向基础仿真信号和开放数据集两种数据进行验证,故设计信号源选择模块对信号进行选择,并将产生的信号作为输入连接到振动信号分析系统。基础仿真信号选取基本波形叠加噪声的形式方便对系统功能进行基础验证,开放数据集以Matlab结构体中数据的形式提供,用于验证振动信号分析系统的实际效果。
运行程序点击信号源选择,根据用户需要选取仿真信号或振动信号产生相应数据。在仿真信号中用户可以选择发生信号的形状、幅值和频率等,并对叠加噪声的种类和参数进行配置。若用户选择振动信号,则需要配置振动信号的数据名称。
2.3 信号预处理模块
借助LabVIEW声音与振动工具箱和高级信号处理工具箱中时间序列分析功能设计信号预处理模块。
在运行的程序中点击预处理按钮进入预处理参数配置,在其中用户需要选择预处理方式并进行相应处理方式的参数设定。
2.4 信号特征提取模块
信号特征提取模块借助LabVIEW声音与振动工具和高级信号处理工具包从时域、频域和时频域角度对振动信号进行特征提取,利用LabVIEW丰富的控件清晰地显示信号特征。
2.5 文件管理模块
文件管理模块实现对原始数据和测量结果的存储和复现,提供二进制、文本和表格等常用的文件格式。
为验证所设计的振动测试系统对信号分析的正确性,本文面向基础仿真数据和开放振动数据集对振动分析进行验证。
3 系统实验验证
振动测试系统按照由上至下、模块化的思想搭建,测试时同样采取先模块后整体的思路,首先利用基础仿真信号对系统模块的基本功能进行验证,证明系统可以完成振动测试的流程,实现振动分析的功能,如图3所示。之后针对开放的振动数据集对系统进行实例验证,证明系统可以应用于实际的振动数据分析。
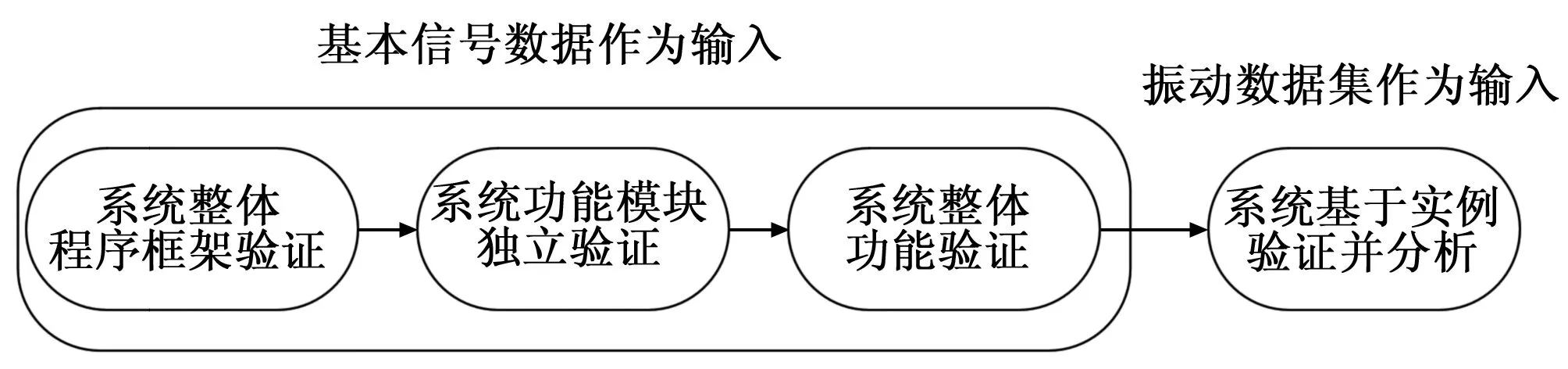
图3 测试思路
3.1 基础仿真验证
在信号源选择模块选取基础仿真信号作为系统的输入。基础仿真信号设计为3个不同频率的正弦信号叠加的形式,方便对滤波、时频域测量以及经验模态分解功能的正确性进行验证。
(1)
式中,参数设定为:T=1/25000,信号点数取1023,方便后续采取1024点FFT,设计3个特征频率为f1=100 Hz、f2=500 Hz、f3=1000 Hz。
3.1.1 预处理测试
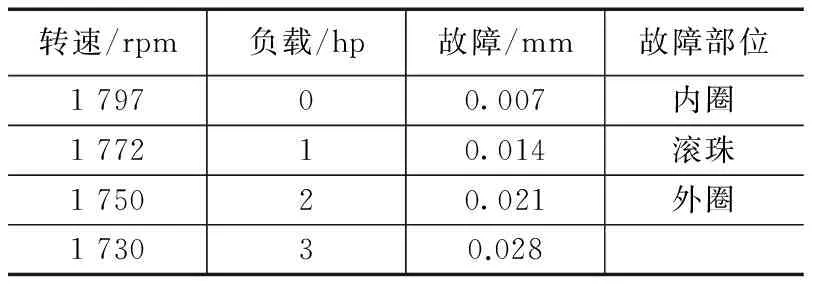
在基础仿真信号上设置不同叠加噪声,预处理方式采取指数平均与去趋势项相结合的方式,以均方根值为预处理效果的参考值,结果如表,斜线上方和下方分别是预处理前后的均方根值。

表1 预处理前后均方根值对比表
由表可见,除高斯噪声外,叠加其他种类噪声时预处理后信号均方根值明显减少,证明信号预处理功能可以一定程度上达到去除干扰的目的。
3.1.2 滤波测试
依次选择不同的通阻模式,设置高低截止频率fh=600 Hz和fl=300 Hz,满足:
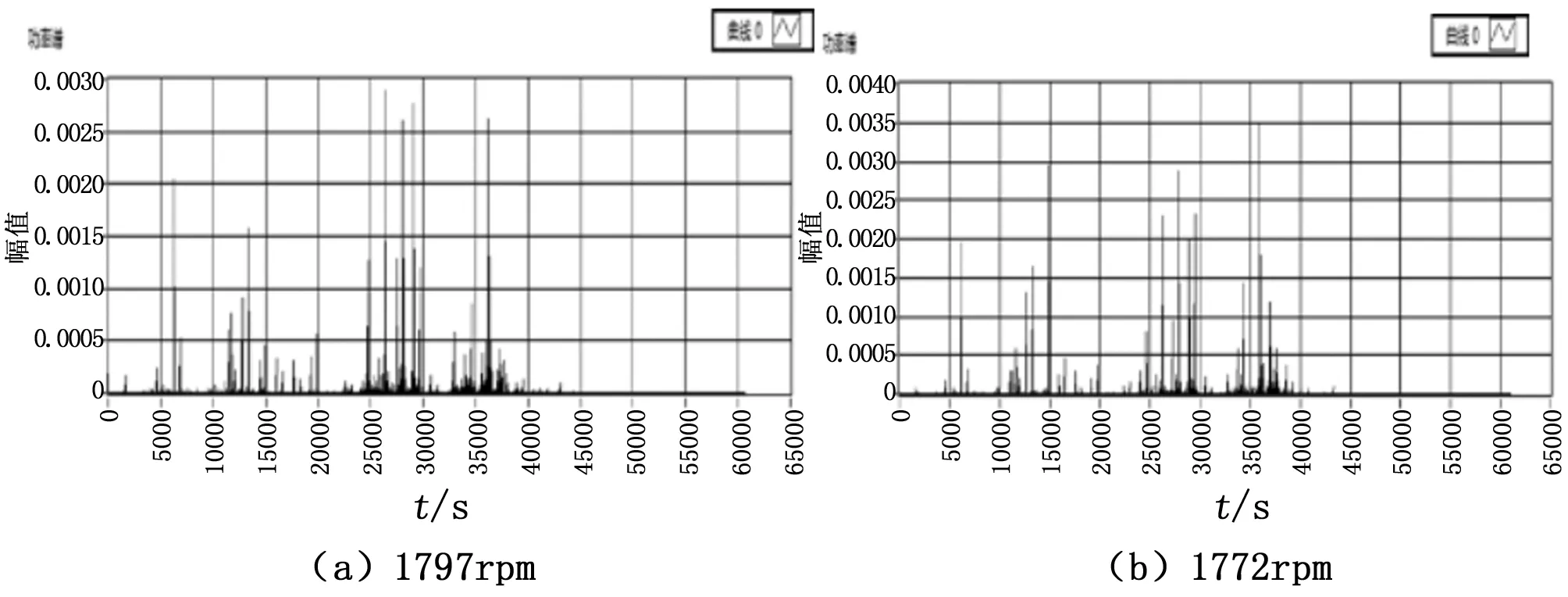
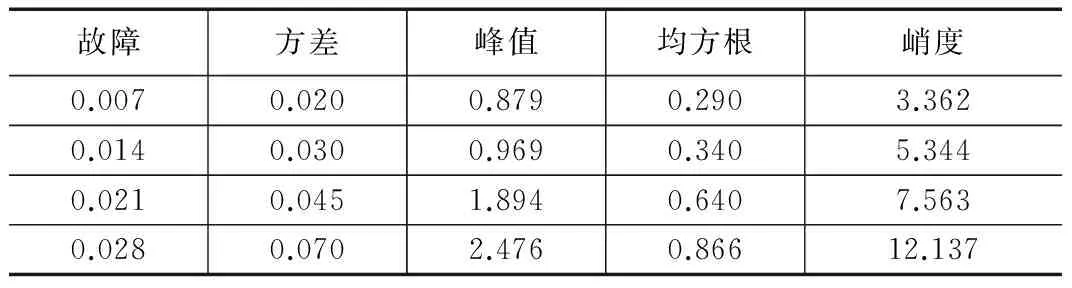
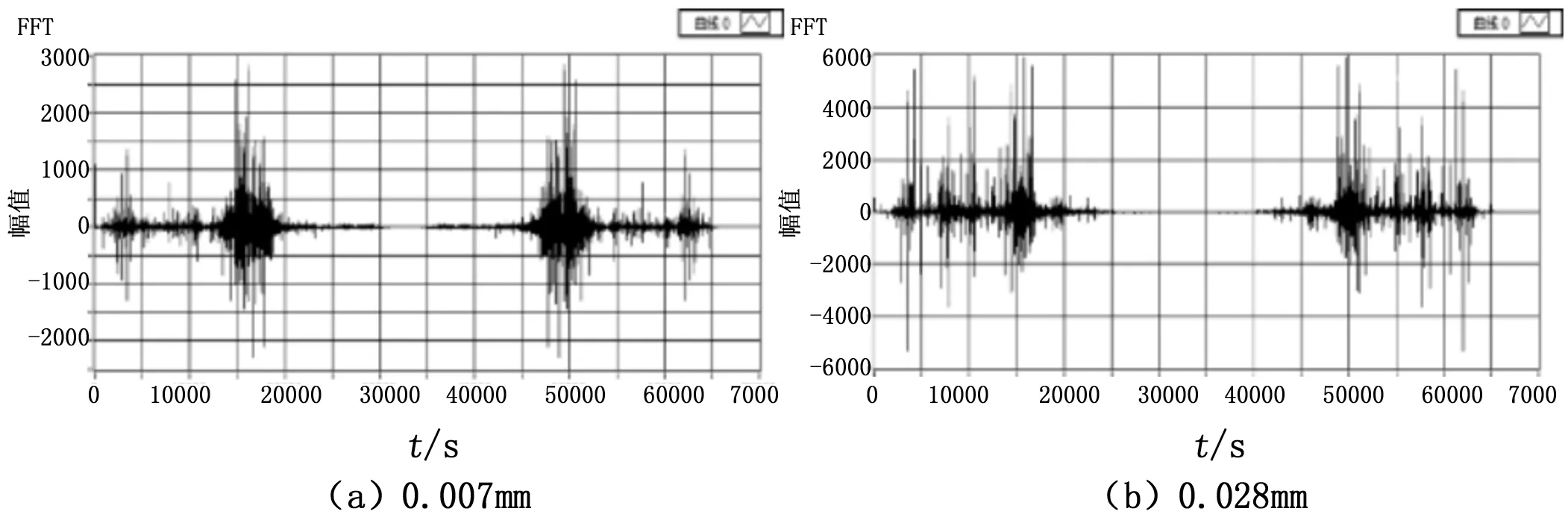
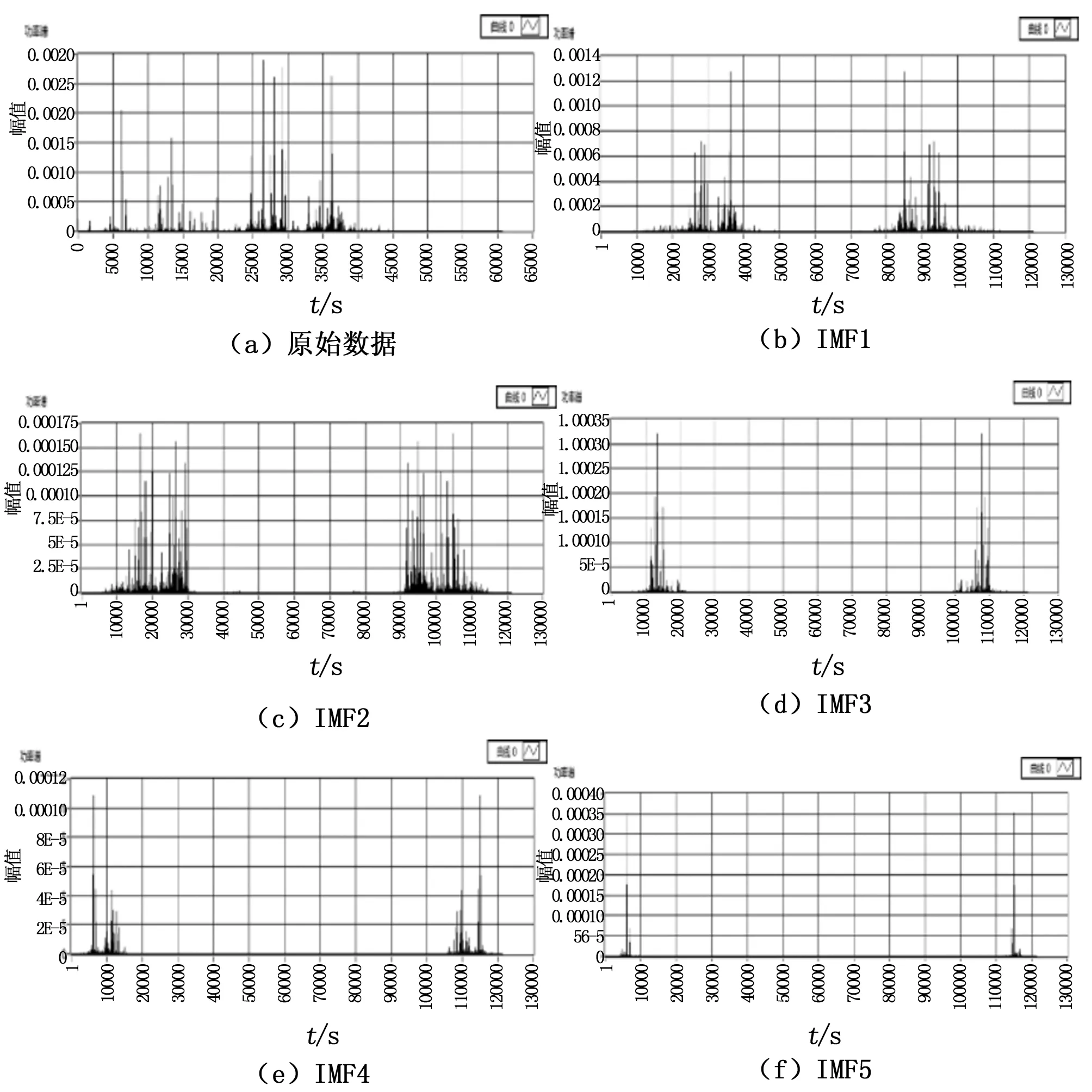
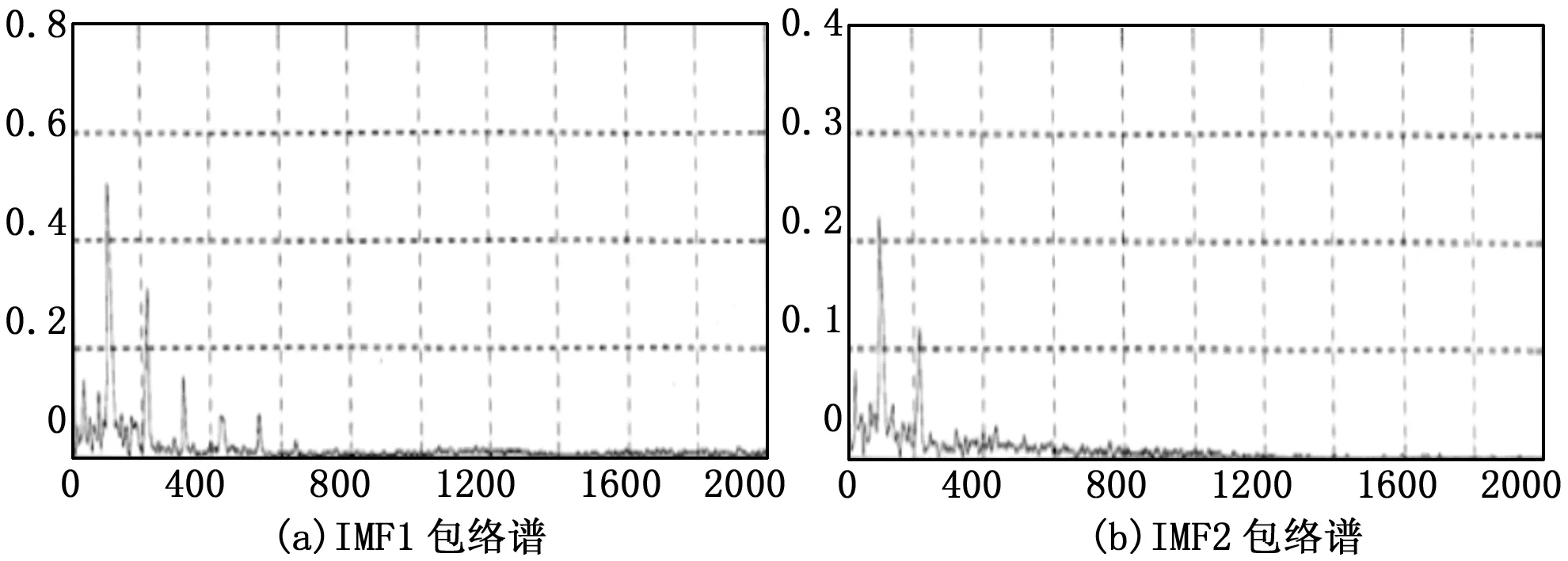
f1 (2) 将滤波后信号进行频谱分析,选取巴特沃斯滤波器得到滤波结果。 图4 滤波结果 由图4滤波后频率成分分布可看出,4种滤波方式低通、高通、带通和带阻滤波在100~1000 Hz频率范围内能够分离不同频率成分,实现滤波功能。 通过以上基于基础仿真信号的测试,验证了振动信号分析系统能够完成振动测试流程,实现基础信号分析功能。 3.2 实例验证 本文选取美国凯斯西储大学轴承中心[16]的开放数据集进行实例验证。该数据集是轴承故障模拟的实验数据包,表中展示了平台的具体条件,提供了4种人工植入的故障点和3个故障部位,在3种转速下实验采集数据。 根据轴承故障数据特点,控制实验条件变化选取振动数据进行对比试验[17]。 表2 凯斯西储大学轴承平台 3.2.1 相同实验条件,对比正常信号与故障信号 实验中在相同实验条件下,选取采样率12 K、负载0 hp、转速1 797 rpm时的正常轴承信号和损伤直径0.007 mm时的故障轴承信号进行对比。经过系统分析,表和图是振动信号分析系统获取的几个时域参量和功率谱图。 由表3中显示的特征参量可以看出,正常信号的统计参量数值较小,而故障信号相对较大。当故障点位于轴承不同位置时,内圈和滚动体故障数据的统计参量数值明显大于外圈故障数据的相应数值,其原因在于轴承内圈与滚动体随轴转动,发生故障时信号变化更为明显。而轴承外圈固定于外部机架上,故障时产生信号变化较小。从图5展示出的信号功率谱也可看出,正常数据得到的功率谱尖峰很窄,说明信号的功率集中在较窄的频率范围内。故障数据的功率谱反应信号的功率分布在较宽的范围内,产生了正常信号中不存在的频率分量。 表3 正常数据与故障数据时域对比 对比正常数据与故障数据可以看出机械设备发生故障时会在各个特征量上发生明显的变化,进一步实验中改变实验条件进行测试。 3.2.2 不同实验条件,对比不同故障信号 在不同实验条件下依次对转速与故障点直径改变的轴承内圈故障数据进行对比测试。 图5 正常信号与故障信号对比 1)固定故障点大小,改变转速: 选取故障点0.007 mm时的内圈故障数据,变电机转速进行测试。 选取系统提取出的部分信号特征如表4和图6。从时域参量和功率谱图中可以看出随转速增加,时域参量有所增大,信号功率所在的频率范围有所变化,但时域和频域特征变化均不明显。 表4 损伤直径0.007 mm内圈轴承测试 图6 不同转速信号功率谱 2)固定转速改变故障点大小: 选取转速为1 797 rpm时的内圈故障数据,改变故障点大小进行测试。 系统获取到的部分信号特征如表5和图7。由系统提取出的参量发现,故障特征随故障点增大而逐渐明显。另外,不同于故障点大小相同改变转速时信号特征变化不明显的情况,当故障点大小变化时故障特征变化明显,说明在这个故障范围内故障点大小相比于转速对机械设备影响更大。 3)Hilbert-Huang法验证: 选取负载0马力、转速1 797 rpm、损伤直径0.007 mm的轴承内圈故障数据进行经验模态分解。首先获取本征函数个数为19个,对每个本征函数计算与原始信号的相关系数,选取前5个本征函数进行功率谱分析。 表5 转速1797 rpm内圈轴承数据 图7 不同故障点频谱 由图8可以看出,经过经验模态分解将频率成分较为复杂的原始信号分解成多个频率成分较为单一的信号。对IMF1和IMF2求包络谱,得到图9。由包络谱图可以更清晰地看出,前两个本征函数包含的频率大致相同,均由故障特征频率及其倍频组成,与轴承故障原理相符[15],系统分析出的特征频率为106.8 Hz,而理论计算值为105.9 Hz,相对误差为0.84%。 图8 前5个本征模量功率谱 图9 本征模量包络谱 经过实例验证,本文设计的振动信号分析系统能够对实际振动信号进行基本分析和特征提取,可以为进一步算法学习和模式识别提供数据基础。 本文结合振动测试的一般流程,完成振动信号分析系统的开发,并面向仿真数据和开放振动数据集进行测试,测试结果表明具备实现振动信号分析的完整流程的能力,能对实际振动信号进行基础分析。同时系统具有良好的扩展性,提供可配置的参数设计、清晰的结果显示及友好的人机交互界面,可作为振动测试的基本流程平台。 由于缺少配合数据采集模块的大量实验,系统目前只实现了普适性的信号分析方法,不能实现针对性的振动信号分析,算法有待优化。同时,精度指标选取不够严格,需要进一步优化。 [1] Shen C Q. Research on fault diagnosis and prognosis for key components of rotating machinery[D].Anhui Province: University of Science and Technology of China, 2014. [2] 张邦成, 陈珉珉, 尹晓静. 基于谐波小波和Hilbert的滚动轴承故障诊断方法[J]. 现代制造工程, 2015, 6: 27-30. [3] 赵海峰. 基于HHT的往复压缩机故障诊断研究[D]. 黑龙江: 东北石油大学, 2011. [4] 孟 宗, 李姗姗. 基于小波改进阈值去噪和HHT的滚动轴承故障诊断[J]. 振动与冲击, 2013, 32(14): 204-208. [5] 张 亢, 程军圣, 杨 宇. 基于局部均值分解的阶次跟踪分析及其在齿轮故障诊断中的应用[J]. 中国机械工程, 2011(14). [6] 康海英, 栾军英, 郑海起. 基于阶次跟踪和HHT边际谱的轴承故障诊断研究[J]. 振动与冲击, 2007(06). [7] 岳晓峰, 朱成伟. 阶次分析在变速箱故障诊断中的应用及其研究[J]. 自动化仪表, 2015, 6(36). [8] 王元生, 任舒心, 杨永峰. 基于盲源分离与小波降噪的旋转机械故障分析[J]. 机械科学与技术, 2012, (5):726-730. [9] 纳跃跃. 频域盲源分离算法研究及其在高速列车噪声成分分离中的应用[D]. 北京: 北京交通大学, 2014. [10] 于丽霞. 虚拟仪器在发动机振动信号处理中的应用研究[D]. 山西: 中北大学, 2008. [11] 肖立波, 任建亭, 杨海峰. 振动信号预处理方法研究及其MATLAB实现计算机仿真[J]. 计算机仿真, 2010, 27(8): 330-333, 337. [12] 李舜酩, 郭海东, 李殿荣. 振动信号处理方法综述[J]. 仪器仪表学报, 2013, 34(8): 1908-1912. [13] 龙 源, 谢全民, 钟明寿. 爆破震动测试信号预处理分析中趋势项去除方法研究[J]. 工程力学, 2012, 29(10): 63-68. [14] 王金福, 李富才. 机械故障诊断的信号处理方法: 频域分析[J]. 噪声与振动控制, 2013, (1): 173-180. [15] 夏 娟. 基于小波变换的齿轮振动信号分析方法研究[D]. 陕西: 西北工业大学. [16] 美国凯斯西储大学, 轴承数据中心[EB/OL]. http://csegroups.case.edu/bearingdatacenter/pages/download-data-file. [17] 张 乾. 基于振动信号的轴承状态监测和故障诊断方法研究[D]. 湖南: 中南大学, 2012. Design of Vibration Signal Processing System on LabVIEW Tang Yi1,Li Qi2,Wang Wenjuan3,Ma Yuntong1,Liu Wang1 (1.Department of Automatic Test and Control, Harbin Institute of Technology, Harbin 150080, China;2.Institute of UAV, Third Research Academy, CASIC, Beijing 100074, China;3.Beijing Electro-Mechanical Engineering Institute, Beijing 100074, China;) In order to meet the needs of fault diagnosis on machines, we designed the vibration signal processing system. Using the graphical development tool of LabVIEW, we realize the process of vibration analysis and basic signal analysis methods. The system is able to preprocess the original vibration signal and extract the features on time, frequency and time frequency domains. We used simulation signals and open vibration databases to do tests of functions of the system. Choosing a set of datas based on the Case Western Reserve University Bearing Data Center Website as an example, the results tells that the vibration signal processing system we designed can identify the frequency of fault with a relative error of 0.84%, and has the advantages of flexible parameter setting, visually displayed results and strong extendibility, providing the basic platform for the vibration testing which is used to realize fault diagnosis on machines. fault diagnosis; vibration test; signal analysis; LabVIEW 2015-08-27; 2015-09-25。 唐 奕(1993-),男,辽宁沈阳人,硕士研究生,主要从事测控技术方向的研究。 1671-4598(2016)06-0218-05DOI:10.16526/j.cnki.11-4762/tp TP391;TN A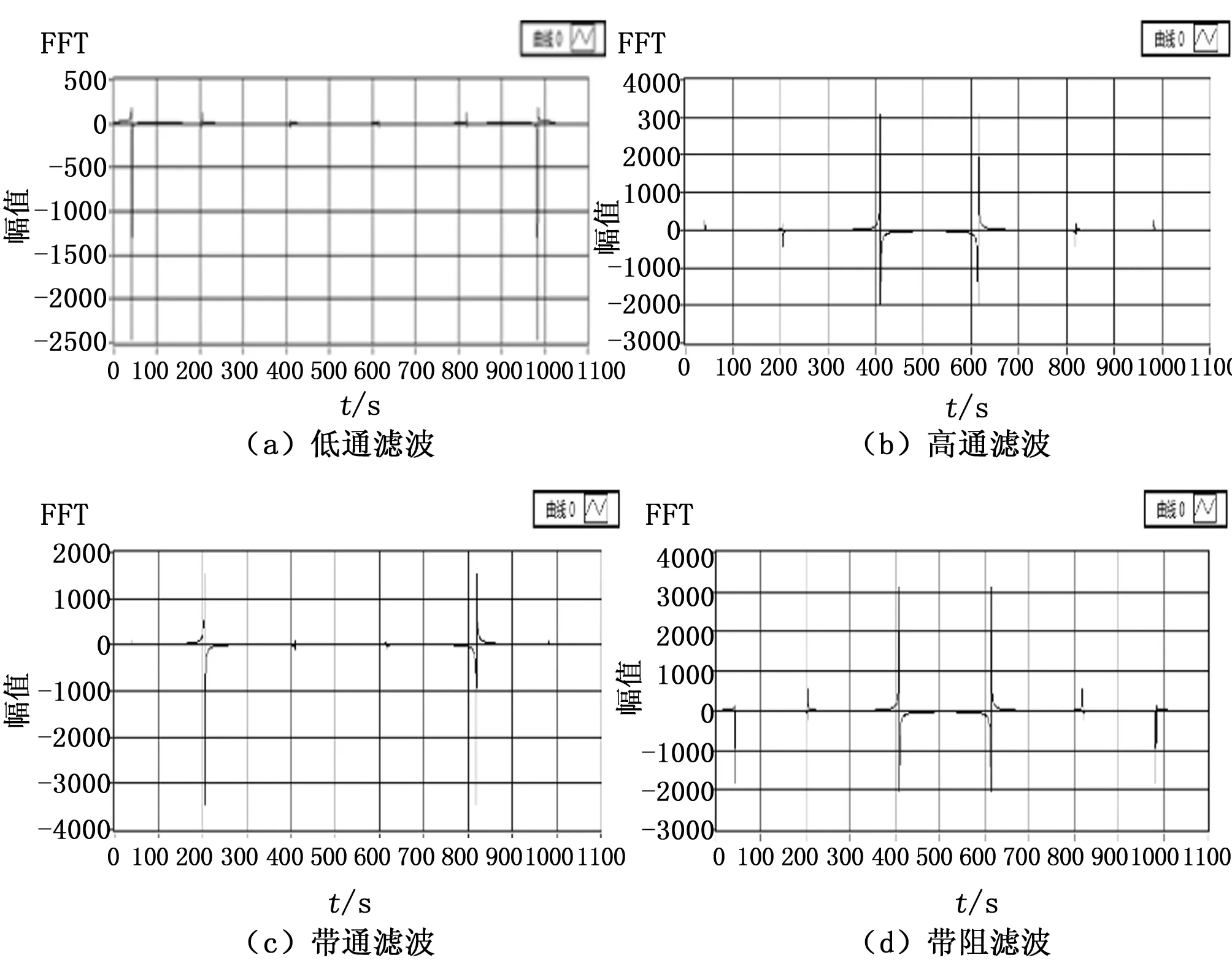
4 结论

