应用蒙特卡罗方法计算弹丸偏心距

张晋华，闻 泉，王雨时，张志彪

(南京理工大学机械工程学院，江苏 南京 210094)



应用蒙特卡罗方法计算弹丸偏心距

张晋华，闻 泉，王雨时，张志彪

(南京理工大学机械工程学院，江苏 南京 210094)

针对目前难以准确测量弹丸偏心距的问题，提出利用蒙特卡罗方法模拟计算弹丸偏心距。计算过程中将弹丸分解成相互独立的基本单元，通过计算各基本单元的质量和质心位置，仿真得出弹丸偏心距的分布规律。仿真结果表明，弹丸偏心距近似服从瑞利分布和威布尔分布，弹丸质量服从正态分布，与实测数据分析结果吻合，可以给引信弹道炸分析提供参考。分析表明，减少弹体加工过程中的装夹次数能有效减小弹丸偏心距。

引信技术；蒙特卡罗方法；偏心距；计算机模拟

0 引言

高速旋转弹丸在飞行过程中以锥形运动螺旋前进，这种运动方式保证了弹丸的飞行稳定性。由于弹丸零部件制造误差(主要包括尺寸误差和同轴度误差)和装配间隙，使得旋转弹丸的旋转轴线并非就是弹丸的几何轴线。当弹箭外形不对称或者由于质量分布不对称使质心不在弹轴上时，会产生对质心的力矩，导致弹箭绕质心转动[1]。引信及其零部件所受弹道环境力，与此绕质心运动以及该质心的位置密切相关。因此，准确获取弹丸偏心距，对于弹丸外弹道特性分析和计算以及其引信复杂受力环境分析和弹道炸原因查找，都具有重要意义。文献[2] 指出，弹丸存在偏心距即径向质心偏移量时会引起引信无返回力矩钟表机构延期解除保险距离散布，弹药生产过程中需对弹丸偏心距加以控制。准确计算旋转弹丸偏心距是弹丸设计、引信设计、弹道分析计算和弹丸稳定性研究的重要基础之一。

弹丸偏心距较小，目前难以准确测量。生产过程中，对弹体偏心距的控制主要是通过检测和控制弹体壁厚差来间接保证的。

文献[3]在未考虑弹体壁厚差的前提下，用统计法估算了径向间隙和同轴度误差引起的引信球转子旋转偏心。文献[4—5]利用弹丸结构特征参数实测数据拟合其数学分布，分别指出一种82 mm口径迫击炮弹偏心距服从威布尔分布和瑞利分布，一种155 mm口径火炮榴弹质量服从正态分布，而偏心距分布接近于威布尔分布和瑞利分布。文献[6]在不考虑弹丸质心相对于其几何轴线偏移量的前提下，利用蒙特卡罗方法模拟了引信机构的旋转偏心，同时指出因旋转偏心所产生的引信机构离心惯性力以及由此所产生的约束反力及其沿轴向的摩擦力都不可忽略。

目前未见国内外有关于旋转弹丸偏心距计算机仿真研究的文献。文献[6]的方法虽不能计算某一发特定引信的偏心距，但可以找出总体散布范围，工程上可以用于估算其影响。本文按照文献[6]的思路，利用蒙特卡罗方法计算旋转弹丸偏心距。

1 蒙特卡罗方法

1.1 蒙特卡罗方法简介

蒙特卡罗方法也称为随机模拟方法，其基本思想是，为了求解数学、物理、工程技术以及生产管理等方面的问题，首先建立一个概率模型或随机过程，使它的参数等于问题的解，然后通过对模型或过程的观察或抽样试验来计算所求参数的统计特征，最后给出所求解的近似值[7]。

对于多维随机函数Z=f(X1,X2,X3,…,Xn)，当已知其中每一个随机变量的分布和分布参数时，就可利用蒙特卡罗方法确定函数Z的统计。当完成大量统计计算(例如105次)后，随机函数Z便会出现与现实状态相似的分布规律。蒙特卡罗方法的理论基础是大数定理和伯努利定理。只要独立试验次数足够大，这两个定理就能成立。因此，只要进行足够大量的计算，蒙特卡罗方法的应用就几乎没有限制[8]。

1.2 蒙特卡罗方法的计算机实现

使用蒙特卡罗方法解决问题时必然会用到随机数或更常见的伪随机数。计算机产生伪随机数的方法有多种，其中应用最为广泛的是乘同余法。

乘同余法的递推公式为[9]：

xn+1=λxn(modM)

(1)

rn=xnM-1

(2)

上式的含义为用M去除λxn，得到的余数为xn+1，其中λ、x0和M为预先选定的常数。将得到的序列(x1,x2,x3,…xn)除以M，即可得到区间[0,1]之间的随机数(r1,r2,r3,…rn)[8]。

在区间[0,1]内随机数ri已经生成的情况下，(a,b)区间内服从均匀分布的随机数可按下式抽取：

Ri=(b-a)ri+a

(3)

对服从正态分布(μ,σ)的随机数，可按下式抽取：

Ri=tN01,jσ+μ

(4)

式中tN01,j为标准正态分布抽样。根据复合抽样方法，可按下式计算[7]：

(5)

对服从瑞利分布的随机数，可按下式抽取：

(6)

2 利用蒙特卡罗方法计算旋转弹丸偏心距

2.1 基本假设

在对弹丸偏心距进行分析和计算前，做如下假设：

1)弹体同轴度误差方向随机，方向角在[0,360°]内均匀分布，同轴度误差按瑞利分布[9]。99.99%的同轴度误差散布范围与同轴度公差相同。

2)除弹体同轴度误差外，其余尺寸均符合正态分布，其散布中心为公差带中心，散布范围8 s为公差带宽度T。这相当于假设工艺能力系数为8s/6s=1.33，也未考虑生产操作过程中为降低废品率保证尺寸修复裕量而使实际尺寸分布中心并不位于公差带中心而是略偏向于最大实体状态的实际情况。由于正态分布只有99.99%(即散布范围8 s对应的置信度)的取值在公差带宽度T内，故在蒙特卡罗模拟时要剔除在公差带T之外的抽样尺寸即不合格尺寸[6]。

3)弹体材料为均质材料。

4)忽略纸垫的影响。

5)不考虑弹体表面不圆度等形状误差。

6)不考虑弹体表面处理后镀层及装配涂漆的影响。

7)不考虑倒角和圆角尺寸偏差。

8)弹带槽按辊花前尺寸计算。

9)假设螺纹中径服从正态分布，公差带宽度为中径极值之差。

10)假设战斗部装药密度均匀，不考虑引信、弹带、炸药柱及曳光管自身的径向偏心距，弹带、炸药柱、曳光管相对于弹丸中轴线的偏心由弹体上相应孔决定，引信、弹带、炸药柱、曳光管质量已知。

2.2 仿真方法

本文将旋转弹丸分解为相互独立的多个基本回转单元，通过计算各回转单元的质量和质心位置X1,X2,X3,…,Xn，则弹丸的质心位置可看作这些随机变量的多维随机函数Z=f(X1,X2,X3,…,Xn)。对该多维随机函数的统计规律进行研究，就可得出弹丸径向质心位置的分布规律。具体应用方法和步骤与文献[6]的基本相同。

3 算例

3.1 37 mm口径高炮榴弹径向质心位置分布

一种37 mm口径高炮榴弹弹丸结构如图1所示，弹丸弹体结构如图2所示。

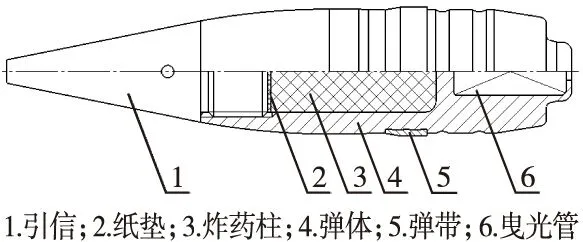
图1 一种37 mm口径高炮榴弹弹丸结构图Fig.1 The structure drawing of 37 mm-caliber projectile

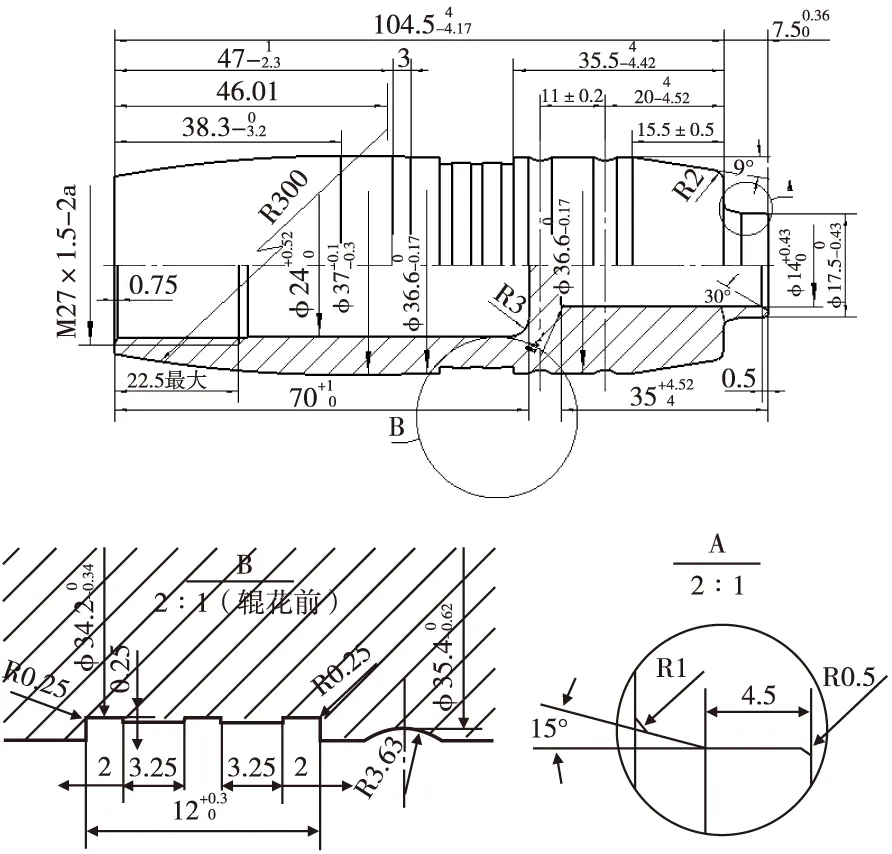
图2 一种37 mm口径高炮榴弹弹体结构Fig.2 The structure drawing of 37 mm-caliber projectile body

由弹丸产品图上技术要求可知：

1)弹口螺纹M27×1.5对外圆柱部的同轴度误差不超过0.25 mm；

2)上药室孔(φ24)对外圆柱部的同轴度误差不超过0.25 mm；

3)定心部(φ37)对外圆柱部的同轴度误差不超过0.075 mm；

4)弹带对外圆柱部的同轴度误差不超过0.075 mm。

从生产工艺分析：

1)除弹带部和定心部外，假设弹体外表面其它部分对外圆柱部的同轴度误差都不超过0.25 mm；

2)假设下药室孔对外圆柱部的同轴度误差也为不超过0.25 mm。

将弹体分解为弹头部、定心部、连接段、圆柱部、弹带部、环槽部、尾锥部、螺纹孔、上药室孔和下药室孔共10部分，如图3所示，分别计算各部分体积。其中螺纹孔体积按螺纹中径计算，螺纹孔中径及其它长度尺寸按服从正态分布计算。在计算各部分体积时，同一尺寸可能会被多次使用，在每一次计算弹丸偏心距时，同一尺寸的值在计算各部分体积过程中保持不变。弹体材料密度ρ=7.85 g/cm3。

从工厂调研可知，目前该弹体的加工方法主要为冷挤压与车削。工序为：冲床下料、整形、一挤、二挤、引伸、切口、收口、车定心部、车弹尾曳光管孔、车弹带槽、辊花、扩螺纹孔、铰药室孔、车内螺纹、磨定心部、检验。挤压过程中，主要通过模具定位孔定位坯料，共需装夹5次；车削过程中，主要通过通用工装装夹弹体，共需装夹7次。因此可以假设各部分相对于圆柱部的同轴度误差不相关。

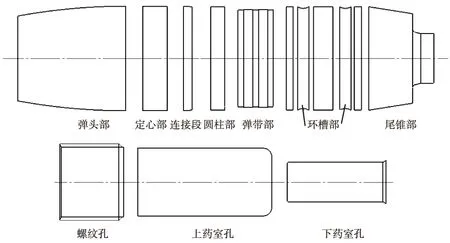
图3 一种37 mm口径高炮榴弹弹体分解成基本回转单元Fig.3 A 37 mm-caliber projectile body was broken into basic rotary units

从弹丸设计图纸可得37 mm口径高炮榴弹弹丸偏心距计算原始数据如表1所列。

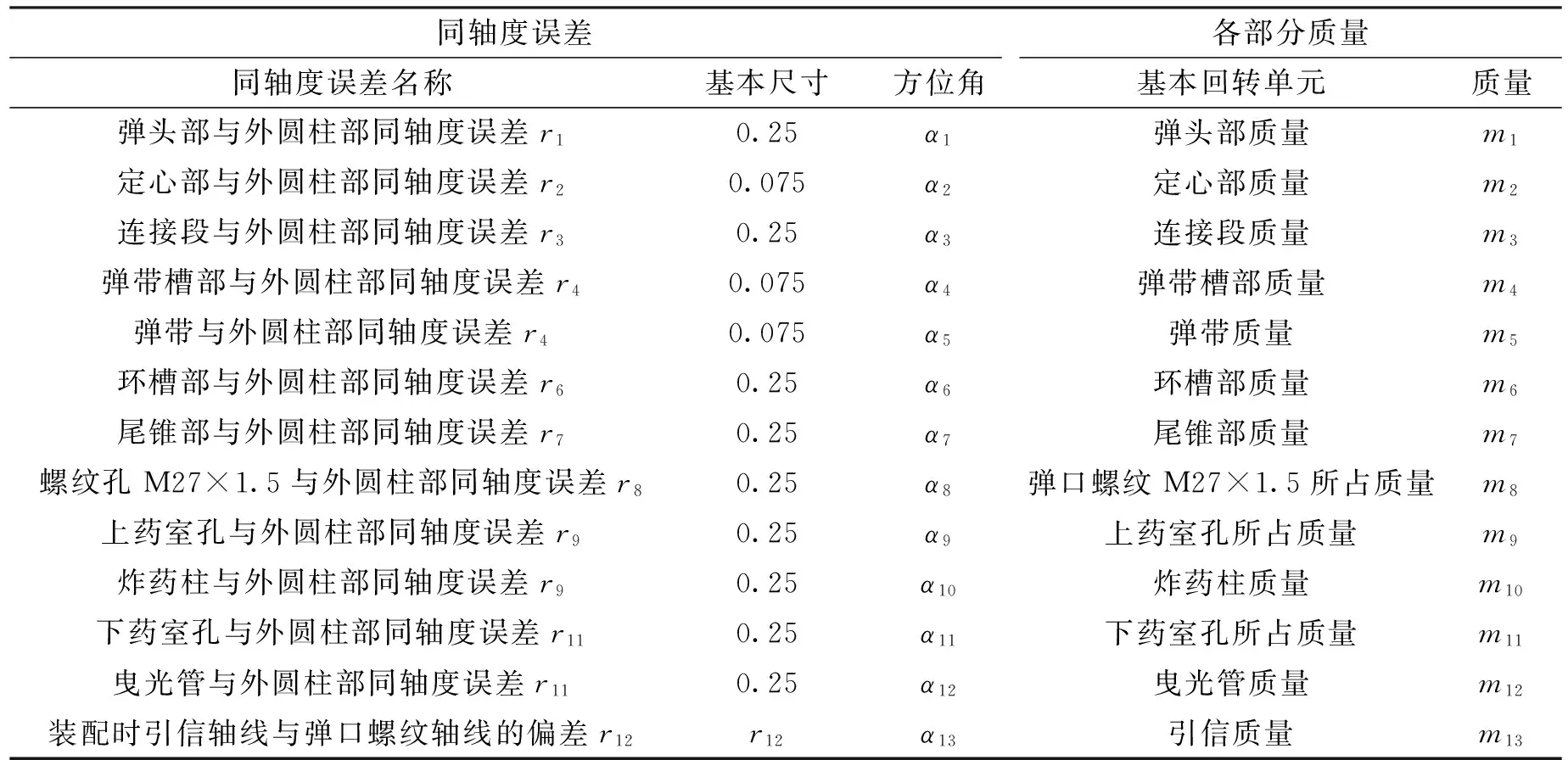
表1 37 mm口径高炮榴弹弹丸偏心距计算原始数据

表1中r12为装配时引信轴线与弹口螺纹轴线的偏差。由于弹口螺纹中径与引信螺纹中径大小不同，所以在装配过程中引信轴线与弹口螺纹轴线很可能会不重合。假设引信轴线与引信螺纹轴线重合，则r12为弹口螺纹中径与引信螺纹中径之差。

表1中各部分质量mi按立体解析几何学方法解算得出，如计算环槽部质量m6：

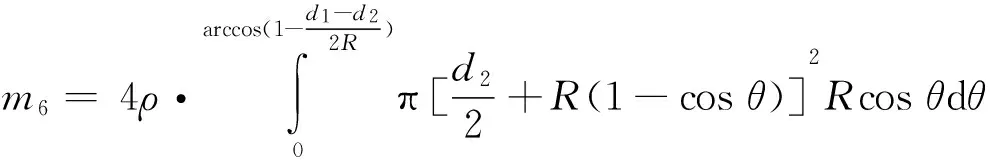
(7)

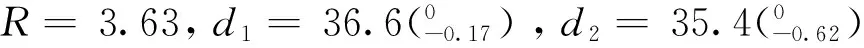
假设表1中同轴度误差服从瑞利分布，用MATLAB命令raylrnd(B)产生随机数模拟同轴度误差。由验算知，随机数命令raylrnd(0.059)可保证其值有99.99%在公差带[0,0.25]内，而随机数命令raylrnd(0.017)可保证其值有99.99%在公差带[0,0.075]内，在蒙特卡罗模拟时要剔除在极限尺寸范围之外的值(约有0.01%)。

假设弹体各部分同轴度误差不相关，以弹体外圆柱部中轴线为基准，则弹丸的径向质心位置为：rx=[m1r1cos α1+m2r2cos α2+m3r3cos α3+(m4+m5)r4cos α4+m6r6cos α6+m7r7cos α7-m8r8cos α8+

(8)

ry=[m1r1sin α1+m2r2sin α2+m3r3sin α3+(m4+m5)r4sin α4+m6r6sin α6+m7r7sin α7-m8r8sin α8+

(9)

弹丸偏心距r为:

(10)

应用MATLAB软件编程对弹体偏心距进行蒙特卡罗模拟，在模拟过程中对于每个组成环都以105个合格抽样值代表整体，则可得该37 mm口径高炮榴弹弹丸偏心距分布直方图，如图4所示。图5为该37 mm口径高炮榴弹弹丸质量分布直方图。同理可得弹体偏心距分布直方图和弹体质量分布直方图分别如图6和图7所示。

3.2 偏心距分布曲线拟合和参数估计

由图4和图6走向趋势判断，该37 mm口径高炮榴弹弹丸偏心距和弹体偏心距分布比较接近于瑞利分布和威布尔分布。由图5和图7走向趋势判断，该高炮弹丸质量和弹体质量分布接近于正态分布。

对弹丸偏心距分布曲线进行拟合，经筛选，瑞利分布和威布尔分布的拟合曲线与原始数据曲线基本吻合，图8给出了该37 mm口径高炮榴弹弹丸偏心距的瑞利分布和威布尔分布拟合曲线，图9给出了该高炮弹丸质量的正态分布拟合曲线，经拟合可得瑞利分布的参数：尺度参数b=0.034 633 8；威布尔分布的参数：形状参数a=0.048 474 4，尺度参数b=1.911 04；正态分布的参数：m=728.568，s=1.615 67。图10给出了该高炮榴弹弹体偏心距的瑞利分布和威布尔分布拟合曲线，图11给出了该高炮榴弹弹体质量的正态分布拟合曲线，经拟合可得瑞利分布的参数：尺度参数b=0.044 257 4；威布尔分布的参数：形状参数a=0.061 804 3，尺度参数b=1.893 46；正态分布的参数：m=492.202，s=1.626 22。

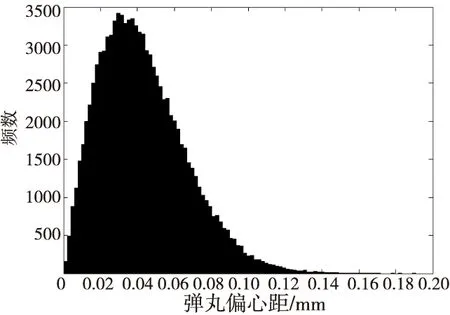
图4 37 mm口径高炮榴弹偏心距分布直方图Fig.4 Distribution histogram of eccentricity of 37 mm-caliber projectile

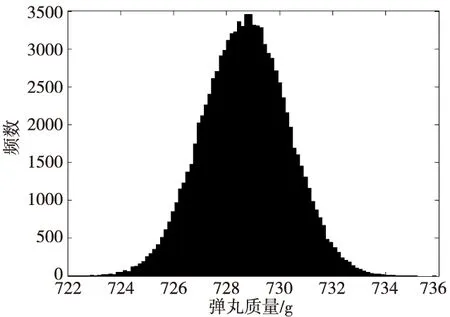
图5 37 mm口径高炮榴弹质量分布直方图Fig.5 Distribution histogram of quality of 37 mm-caliber projectile

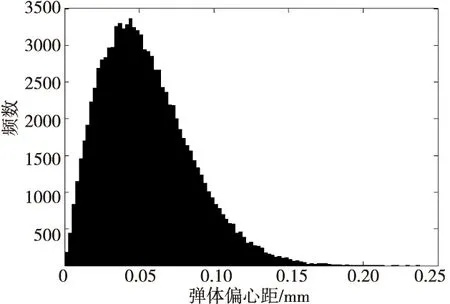
图6 37 mm口径高炮榴弹弹体偏心距分布直方图Fig.6 Distribution histogram of eccentricity of 37 mm-caliber projectile body

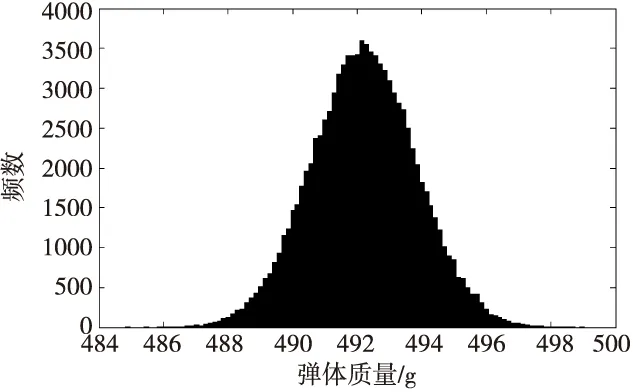
图7 37 mm口径高炮榴弹弹体质量分布直方图Fig.7 Distribution histogram of quality of 37 mm-caliber projectile body

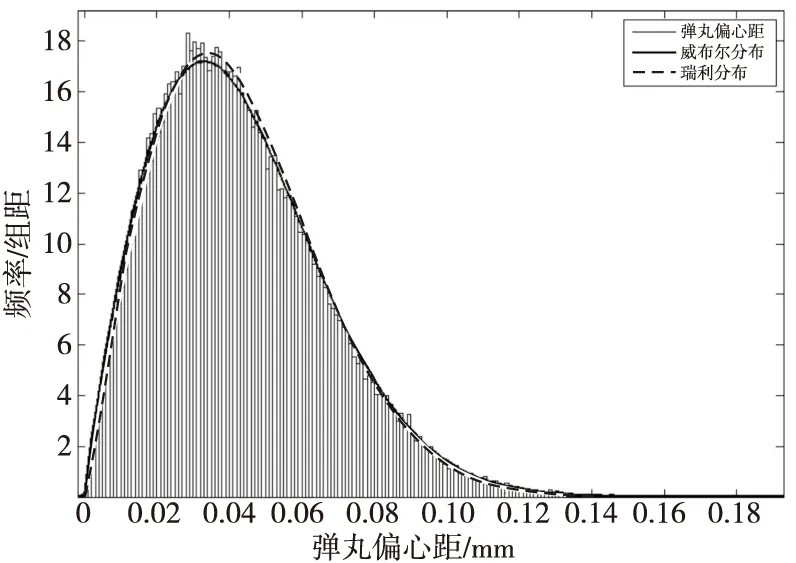
图8 37 mm口径高炮榴弹弹丸偏心距瑞利分布和威布尔分布的拟合曲线Fig.8 The fitted curve of rayleigh distribution and weibull distribution of eccentricity of 37 mm-caliber projectile

图9 37 mm口径高炮榴弹弹丸质量正态分布的拟合曲线Fig.9 The fitted curve of normal distribution of the quality of 37 mm-caliber projectile

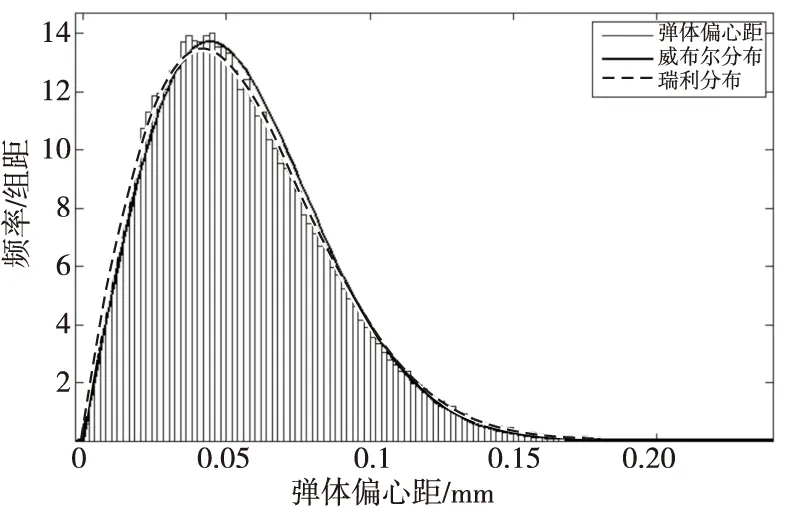
图10 37 mm口径高炮榴弹弹体偏心距瑞利分布和威布尔分布的拟合曲线Fig.10 The fitted curve of rayleigh distribution and weibull distribution of eccentricity of 37 mm-caliber projectile body

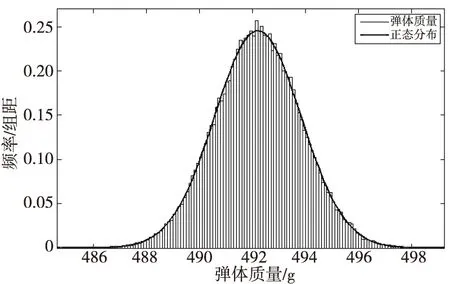
图11 37 mm口径高炮榴弹弹体质量正态分布的拟合曲线Fig.11 The fitted curve of normal distribution of quality of 37 mm-caliber projectile body

3.3 偏心距分布拟合检验

Kolmogorov-Smirnov检验可以作双侧检验，检验样本是否服从指定的分布，也可以作单侧检验，检验样本分布函数是否在指定的分布函数之上或之下。对该37 mm口径高炮榴弹弹丸偏心距样本进行K-S检验，检验弹丸偏心距和弹体偏心距是否服从瑞利分布和威布尔分布，弹丸质量和弹体质量是否服从正态分布。结果表明，在显著性水平0.05下，弹丸质量服从m=728.568 g，s=1.615 67 g的正态分布，弹体质量服从m=492.202 g、s=1.626 22 g的正态分布，弹丸偏心距和弹体偏心距近似服从瑞利分布和威布尔分布(在显著性水平0.000 1下，弹丸偏心距和弹体偏心距服从威布尔分布)。偏心距分布类型与基本假设中假设的同轴度误差分布类型接近。

3.4 实测数据验证

现有该37 mm口径高炮榴弹弹体偏心距和弹体质量实测数据50组，分布直方图如图12和图13所示。

经拟合检验可知，在显著水平0.05下，弹体偏心距实测值服从瑞利分布和威布尔分布，弹体偏心距实测值几乎分布在(0,0.07)区间内。由图10可知，弹体偏心距仿真计算值几乎分布在(0,0.14)区间内，且近似服从瑞利分布和威布尔分布。仿真计算是按尺寸极值条件进行的，而实际加工尺寸要留有工艺能力裕度，因此弹体偏心距实测值范围小于仿真值分布范围是可信的。

图12 37 mm口径高炮榴弹弹体偏心距实测数据分布直方图Fig.12 Distribution histogram of test dates of eccentricity of 37 mm-caliber projectile body

图13 37 mm口径高炮榴弹弹体质量实测数据分布直方图Fig.13 Distribution histogram of test dates of quality of 37 mm-caliber projectile body

在显著水平0.05下，弹体质量实测值服从正态分布。弹体质量实测平均值为491.38 g。由图11可知，弹体质量仿真计算值服从正态分布，仿真计算平均值为492.202 g，仿真计算平均值与实测平均值相差0.17%。

弹体偏心距和弹体质量实测数据的分布情况验证了本文方法的可信性。

3.5 分析和讨论

假设弹体内、外表面和弹口螺纹在车床上一次装夹完成加工，定心部精度较高，需用磨床加工，加工弹体过程中需装夹两次，即弹体除定心部外的其他部分与外圆柱部的偏心一致，因本文以外圆柱部中轴线为基准，则可忽略弹体除定心部外的其他部分相对于外圆柱部的同轴度误差。在其他条件保持不变的情况下，可得该状态下该37 mm口径高炮榴弹弹丸偏心距分布直方图如图14所示。图15为瑞利分布和威布尔分布的拟合曲线。经拟合检验可知，在不考虑弹体除定心部外的其他部分相对于外圆柱部的同轴度误差时，在显著性水平0.05下，该37 mm口径高炮榴弹弹丸偏心距不服从尺度参数b=0.030 077 3的瑞利分布，也不服从形状参数a=0.041 851 6、尺度参数b=1.866 36的威布尔分布。

由图14可知，当加工弹体过程中只装夹两次时，弹丸偏心距分布在(0,0.05)区间内，与图4相比弹丸偏心距明显减小。因此，减少弹体加工过程中装夹次数能有效减小弹丸偏心距。

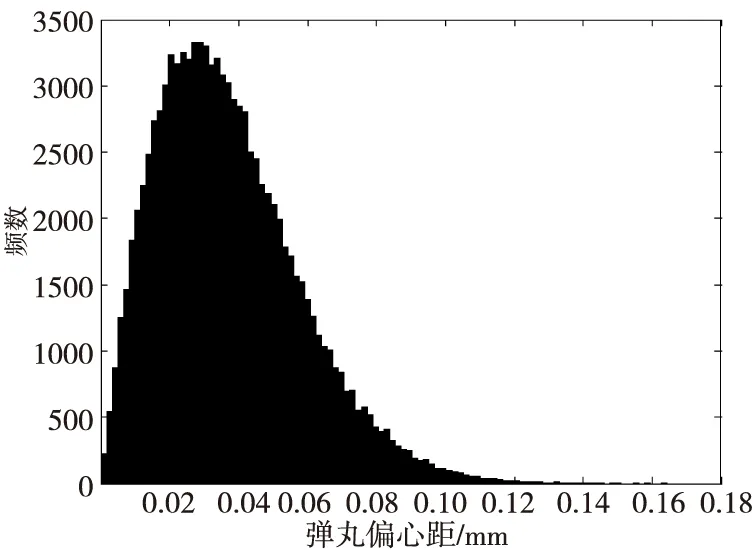
图14 两次装夹时该37 mm口径高炮榴弹弹丸偏心距分布直方图Fig.14 Distribution histogram of eccentricity of 37 mm-caliber projectile when clamping twice

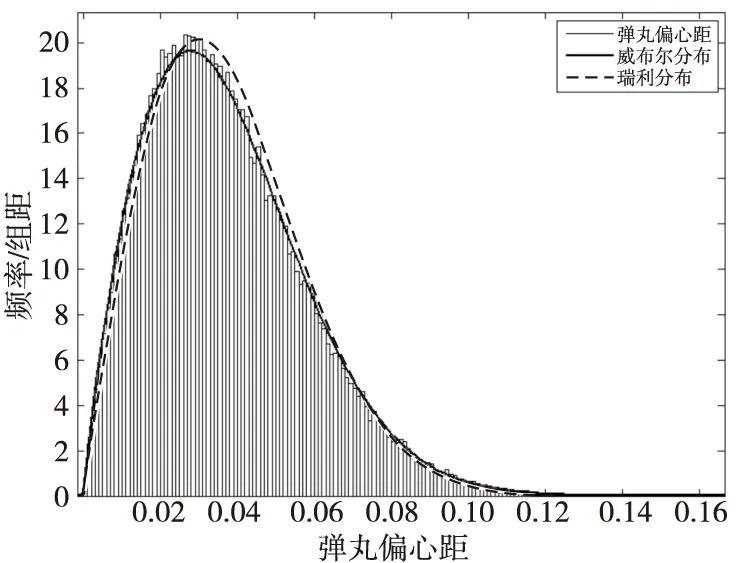
图15 两次装夹时该37 mm口径高炮榴弹丸偏心距瑞利分布和威布尔分布的拟合曲线Fig.15 The fitted curve of rayleigh distribution and weibull distribution of eccentricity of 37 mm-caliber projectile when clamping twice

3.6 在一种105 mm口径火炮榴弹中的应用

根据一种105 mm口径火炮榴弹弹丸产品图，采用与上述相同的计算方法，得出该弹丸偏心距分布直方图和弹丸质量分布直方图，如图16和图17所示。由图16可知，该105 mm口径火炮榴弹弹丸偏心距几乎都分布在(0,0.83)区间内。经拟合检验可知，在显著性水平0.05下，该105 mm口径火炮榴弹弹丸偏心距不服从尺度参数b=0.185 593的瑞利分布，但服从形状参数a=0.249 203、尺度参数b=1.650 86的威布尔分布，弹丸质量服从m=16.450 6、s=0.040 707 2的正态分布。

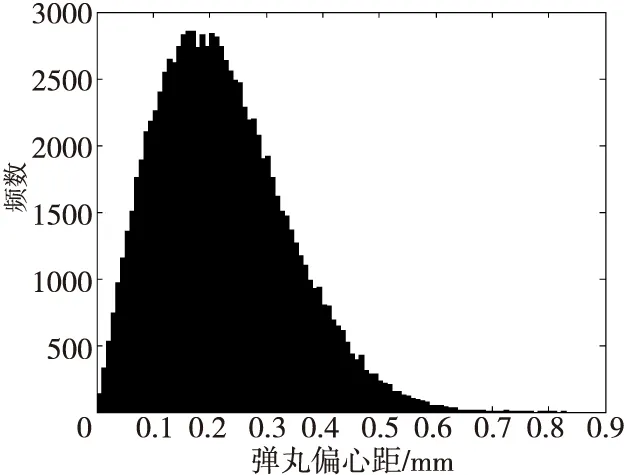
图16 一种105 mm口径火炮榴弹弹丸偏心距分布直方图Fig.16 Distribution histogram of eccentricity of a 105 mm-caliber projectile

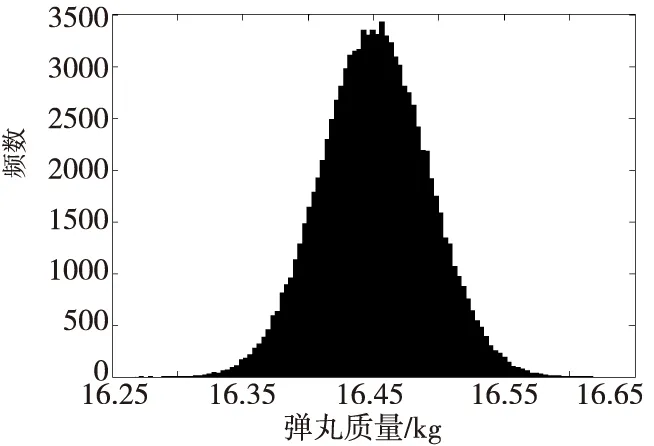
图17 一种105 mm口径火炮榴弹弹丸质量分布直方图Fig.17 Distribution histogram of quality of a 105 mm-caliber projectile

该105 mm口径火炮榴弹弹丸表定质量为16.2 kg，理论计算平均值与表定值相差1.5%，仿真结果可信。

4 结论

本文提出利用蒙特卡罗方法模拟计算弹丸偏心距。计算过程中将弹丸分解成相互独立的基本单元，通过计算各基本单元的质量和质心位置，仿真得出弹丸偏心距和质量的分布规律。

利用蒙特卡罗方法计算一种37 mm口径高炮榴弹及一种105 mm口径火炮榴弹的偏心距和弹丸质量，仿真结果和实测数据分析结果基本吻合，弹丸偏心距近似服从瑞利分布和威布尔分布，弹丸质量服从正态分布。减少弹体加工过程中的装夹次数能有效减小弹丸偏心距。

弹丸偏心距理论最小值是0，最大值与弹径正相关。一种37 mm口径高炮榴弹和一种105 mm口径火炮榴弹弹丸偏心距最大值分别是0.17 mm和0.83 mm。弹丸偏心距最大值约与弹径的1.5次幂呈正比关系。

[1]韩子鹏.弹箭外弹道学[M].北京：北京理工大学出版社，2014：74-75.

[2]张健，李作华，侯小丫，等.弹丸质偏对引信解除保险距离的影响[J].沈阳理工大学学报，2015，34(1)：13-16.

[3]王雨时，何莹台.用统计法计算矢量尺寸链求引信球转子的旋转偏心[J].沈阳工业学院学报，1997，16(1)：1-6.

[4]王晓鹏，王雨时，闻泉，等.某82 mm口径迫弹力学参数分布特性研究[J].弹箭与制导学报，2014，34(4)：73-77.

[5]王晓鹏，王雨时，卢凤生，等.155 mm口径火炮榴弹结构特征数分布特性研究[J].探测与控制学报，2015，37(5):66-72.

[6]闻泉，王雨时，陈会光.引信机构旋转偏心的蒙特卡罗模拟[J].探测与控制学报，2007，29(3)：72-75.

[7]于连璋，吴永，孙德有.形位误差的两种分布率[J].大连铁道学院学报，1989(3)：25-32.

[8]闻泉，王雨时.子母弹径向质心位置的蒙特卡罗模拟[J].弹箭与制导学报，2005，26(2)：403-405.

[9]徐钟济.蒙特卡罗法[M].上海：上海科学技术出版社，1985：5-40.

Projectile Eccentricity Calculation with Monte-Carlo Method

ZHANG Jinhua, WEN Quan, WANG Yushi, ZHANG Zhibiao

(School of Mechanical Engineering, NUST, Nanjing, 210094, China)

In view of the problems that it is difficult to measure the eccentricity of projectiles accurately, a method of calculation for eccentricity of projectiles with Monte-Carlo method was proposed. The projectile was split into basic elements which was independent from each other in the calculation process. The distribution law of the eccentricity of spinning projectile could be simulated by calculating the quality and the centroid position of the basic elements. The simulation results coincided with the measuring results, which could provide reference for the analysis of fuze’s early burst. The results showed that the eccentricity of the projectile obeyed rayleigh distribution and weibull distribution approximately. The projectile mass obeys normal distribution. The eccentricity of projectiles would be reduced significantly when the number of clamping the projectile body on the machine tool was reduced.

fuze technology ; Monte-Carlo method; eccentricity; computer simulation;

2016-03-24

江苏省自然科学基金青年基金项目资助(BK20140786)

张晋华(1990—)，男，江苏南通人，硕士研究生，研究方向：精密机械设计与动力学分析。E-mail:zhangjh204@163.com。

TJ430

A

1008-1194(2016)05-0042-07