计算机模拟在概率论课程教学中的应用
谢晓振+胡小宁


摘要:在理解频率的稳定性、大数定律以及中心极限定理方面上,计算机模拟概率论随机试验有着非常显著的教学效果。本文通过简要分析余数法、混同余法所形成的均匀随机数方法、运用Mathematica软件所形成的一系列分布随机数方法,并借助于计算机技术的假设检验方法对所获取的伪随机数进行假设检验,然后通过蒲丰的投针实验为依据,对数值计算上运用概率思想的蒙特卡洛方法进行简要探讨,希望能够为我国概率论课程教学效率和教学质量的提升带来一定帮助。
关键词:计算机模拟;概率论课程教学;蒙特卡洛方法
中图分类号:G424 文献标识码:A 文章编号:1009-3044(2016)25-0163-02
在概率论的发展历史中可以看出,为了进一步分析和研究随机现象的统计规律,一些老一辈的数学家制定了诸多随机试验,其中最为典型的有蒲丰的投针实验、葛尔顿钉板试验等。这些试验在一定程度上凸显出来老一辈数学家的智慧。因此在现代的概率论课程教学过程中拥有着非常重要的意义。而随着现代科技的不断进步和发展,计算机技术逐渐得到普及,而运用计算机来对早期数学家所设计的随机试验进行实施,能够让概率论教学效果得到有效提升。
1 计算机模拟随机试验中的问题探讨
在很早之前,大部分数学家想要实验都是依靠纯手工的方式,如掷硬币实验就是靠早期数学家一次次抛掷的方法,来严重硬币的正反面出现概率,如表1。
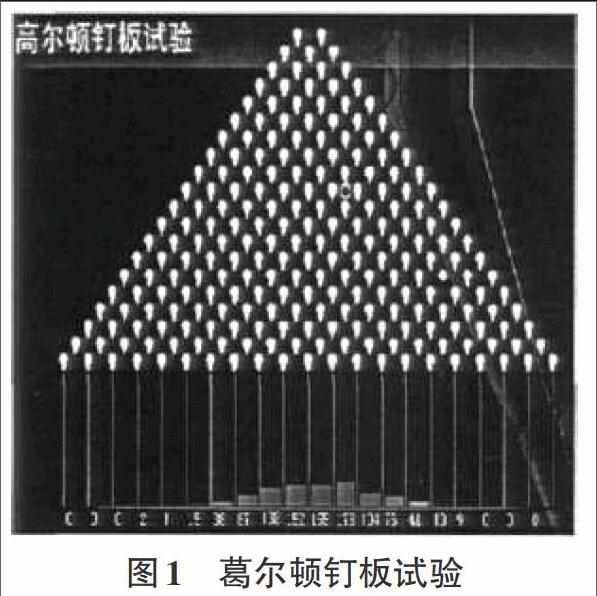
此外还有一个较为经典的葛尔顿钉板试验,其目的是为了验证频率的稳定性,其是在一块斜立木板上,依次钉上钉子,每一个白点代表一个钉子,且钉子之间的距离均都相同,上面钉子刚好处于下面两颗钉子的中心位置,从入口处将一个半径小于钉子间距的小球放入其中,当小球碰撞到第一排钉子后,会以百分之五十的概率滚向左/右下,然后触碰到第二排钉子,以此循环直至小球从某一个格子内滚出为止。当放入小球数量为1时,则事先难以准确地判断出小球会想那个方向的格子滚去,但如果小球数量增多并达到一定数量时,则其底部所呈现的曲线则基本上一致,均呈现一种橄榄球状[1]。由此可得出,小球落入到每个格子的频率均都稳定,而实验中小球构成的曲线则称之为正态分布,见图1。
此外,如果多次测量一个物体的长度,其平均值会是在处于某个固定值左右。而在目标均匀性实验及灯泡寿命试验等一系列重复性实验也均都是浮动在某固定值上。在设计这些试验不仅较为枯燥,而且还消耗较长的时间,尤其是在进行破坏性实验时,例如寿命试验等,则就需要消耗过高的成本,而若将这些试验运用计算机进行模拟试验,则就能让一系列问题得到有效解决,具有非常显著的教学作用。不过从真实试验向计算机模拟试验转变,首先要做的就是有效解决随机数产生、假设检验记忆蒙特卡洛方法等问题。
2 计算机上随机数的形成方法
2.1 均匀随机数的形成
计算机上随机数产生方法中最为常见的有余数法:
令:yn+ 1=λyn(modM),y0=a
再令 xn=yn/M
其中λ,M为任意正数,a为正奇数。先给定y0=a,用M除以λyn所得的余数记为yn+ 1,用yn+ 1/M得到xn.关于参数的选择,从公开报道得知较适用的有:a=1,λ= 517,M= 242。
此外,还有一种较为常用的方法,即混同余法:
令 yn+ 1=λyn+b(modM),y0=a
再令 xn=yn/M
用混同余法得到(0, 1)区间上均匀分布的50个随机数的程序为:m= 2~16; b= 27421;x0= 2;
LinearCong[x_]:=Mod[bx+ 7,m ];data= Table [LinearCong [x ]/m /N,{x, x0, 49+x0}];h=Length[data]
2.2 利用[0,1]区间上均匀分布的随机数和反函数定量得出分布的随机数
将单调上升的连续分布函数或已给分布密度设为F(x),结合(0,1)中均匀分布随机变数,得出方程为F(y)=Y,解出的结果为y=F-1(Y)是以F(x)为分布函数的随机变数。
2.3 通过mathematics软件产生随机数
在外挂软件包mathematics中有一个统计软件包,其中Drscre Distribution能够产生各种分布的随机数。
3 随机数的分布拟合
借助于上述的几种方法所获取的数属于一种伪随机数,这种通过一定计算方法所获取到了数,从本质上讲并不能够称之为随机数,不过能够通过数据整理统计的独立性检验及分布检验方法,让让其得到实践应用。通常分布拟合的步骤流程主要分为三个,首先对数据进行分组,通过对其频数进行统计,将条形图画出,然后既能够大概的获得随机变量所形成的概率密度图,然后在以区间估计均值和方差为基础,实施分布的假设检验[2]。例如:使用一台自动包装机,其打包重量均为100kg,然后从某天生产产品中随机抽取130包进行重量测量。将区间划分成十六个相同区间,均为0.5kg,然后对130个数据在各个子区间中的落下频数和频率进行计算。通过计算机的分组统计命令获取到落在各个小区间的频率,让狗将频数图画出,由图可得出其随机变量为近似服从正态分布。然后将样本的期望和方差计算出来。
4 蒙特卡洛方法
通过蒲丰的投针试验来阐述蒙特卡洛方法,让其教学应用展现出来。在平面上将一个相等距离a的平行线画出来,然后将任意长度l(l 假设针的投掷中心为M,其中心电距离最近一条平行线的距离为x,与平行线之间的构成的夹角以T 表示。由此可得出:0
按照针与一条平行线相交的充分必要条件为x<2/l,则就代表在(a,x)平面上存在一个子集合:G= {(T,x)|x<2/lsinT},见图3中红线以内的区域。由该问题的转变逐步成为R中所分别的均匀投掷点,求G中点的落下概率。结合破努力大数定律为基础可以获得:频率通过l得出相关的概率,然后依据微积分知识得出,G的面积为:SG=∫π0l/2sinTdT=l/2(-cosT)|π0=l。然后从均匀分布定义得出,G中随机点的落下概率为:P=SG/SR=2l/πa,换位思考则得出π=2l/πa,然后在计算机上通过模拟试验将概率P求出,则就能够通过P=SG/SR=2l/πa公式来将π的近似值计算出来[3]。通过对程序的分组统计命令进行运用,这就能够看到投掷针的实际情况,见图4所示。当n所取值不同时,则能够得出π的各个近似值,例如:当n为100000时,则π约为3.13960,不过在第二次进行实验时,就算次数依旧还是选择本次实验一样的10000次,则所得出的结果可能会出现变化。
5 随机模拟在教学上的应用分析
近几年来,在现代概率论课程教学过程中,通过计算机模拟应用能够制定出多个教学动画,其中较为典型的有高尔顿钉板试验、捕鱼问题以及贝努力大数定律等[4]。通过概率论试验可以使传统难以理解的概念逐渐变得既生动又具有抽象性的理论,实现概率论的情绪性和直观性,从而让学生学习概率论的兴趣得到进一步提升。而通过计算机模拟开发的实验及动画,则能够让教师对信息技术的使用能力得到提高,让课程教学效果得到进一步改善[5]。而且,在实验过程中,运用一系列的计算机数学软件,也能够让学生科学计算的能力得到有效培养,对学生的日后发展和学习有着非常关键的作用。
6 总结
总而言之,从应用计算机模型对数学概率论中的典型问题和实验可以得出,计算机模型能够让概率计算和数据处理变得更加简单、便捷,能够让概念的难以理解现象逐渐转化成既生动又具有抽象性的理论,促使其知识越发直观、清晰,从而全面激发学生对概率论的学习兴趣因此,计算机模拟应用于概率论课程教学中,不但能够让教学效率得到提升,而且对教学质量的提高也有着一定的促进作用。
参考文献:
[1] 郝晓斌,董西广.数学建模思想在概率论与数理统计课程教学中的应用[J].经济研究导刊,2010(16):244-245.
[2] 闫磊,杜富强,王博.计算机数值模拟技术在土建专业课程教学中的应用[J].科技信息,2012(1):493+506.
[3] 史娜.SPSS软件在《概率论与数理统计》课程教学中的应用研究[J].甘肃联合大学学报:自然科学版,2012(6):107-110.
[4] 何丽红.加强计算机技术在“概率论与数理统计”课程中的应用[J].高等理科教育,2006,04:42-44.
[5] 韦程东.从大数定律随机模拟谈Excel在概率论与数理统计教学中的应用[J].广西民族学院学报:自然科学版,2002(4):60-63+67.

