反其道而行之——反比例函数y=（k≠0）中k的几何意义的逆向探究

江苏省常州市新北区龙虎塘中学 张 卫

反其道而行之

江苏省常州市新北区龙虎塘中学 张 卫

此文对苏科版反比例函数y=（k≠0）中k的几何意义的探究打破常规，进行了突破性的设计。教学设计带领学生从一个面积一定的矩形（矩形边长不为0）开始，借助几何画板软件通过逆向探究从矩形面积到反比例函数图像逐步引导同学们探究k的几何意义。可以说这样的设计样式新颖，效果显著。

反比例函数；k的几何意义；逆向探究

k的几何意义的探究似乎大家都是这样处理而且看似简单明了，但本人静下心来思考了很长时间，觉得k的几何意义的得出对于学生思维能力的拓展、对于反比例函数本质的认识、对于学生数形结合思想的理解都有着不可替代的作用，于是本人对k的几何意义探究过程作了全新的设计。

【探究片段教学设计】

一、片段学习目标

1.从实际出发，掌握反比例函数k的几何意义，并能灵活利用这一知识点解决数学问题。

2.深刻领会函数解析式与函数图像之间的联系，体会数形结合及转化的思想方法。

3.体验数学的实用性，提高学数学的兴趣。

二、片段教学过程

（一）几何图形与反比例函数

问题1：如果要你画一个面积是12个平方厘米的矩形，它的长与宽固定吗？

请在下面的表格中填写这个矩形可能的长与宽：

矩形的长2 …矩形的宽6 …

追问：这样的矩形可以画____个。

问题2：如果设这个矩形的长为x cm，宽为y cm，你能写出y与x之间的函数关系式吗？

（二）探究反比例函数系数k的几何意义

情景1：用“几何画板”演示取不同的长与宽时，所画的矩形的情形。

以点A 为坐标原点，AB所在直线为x轴，建立如图的平面直角坐标系（如图1）。

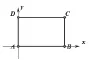
图1

问题1：矩形的顶点C的坐标与矩形的长x（x＞0）与宽y之间有怎样的关系？

用前面填写的表格数据进行绘图（如图2），进一步理解矩形面积与点C坐标间关系。

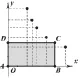
图2

操作：利用几何画板进行动态演示，观察当矩形面积是12个单位时点C在在运动过程中所留下的轨迹。

问题2：当点C在运动过程中所留下的轨迹（如图3）对应怎样的函数？

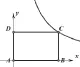
图3

经过上述过程得到一个结论：这样的矩形面积等于反比例函数的系数k=12。（等待修正）

问题3：请你在函数的另一支（第三象限）上任取一点C’，过C’作到x轴的垂线段C’B’，过C’作到y轴的垂线段C’D’，设C’的坐标为（x，y），你能尝试着说明上面我们得到的结论仍然成立吗？（再次尝试）

问题4：如果当反比例函数的图像在二、四象限时（即k＜0时），上述情况仍然成立吗？

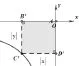
图4

修正结论：这样的矩形面积等于|k|。

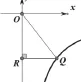
图5

追问：如图5，点Q在第四象限的图像上，过Q作y轴的垂线段QR，垂足为R，所得三角形△QOR的面积与k有怎样的关系？例题讲解：如图6，函数y=（x＞0）的图像相交于点P（a，b），过P作x轴、y轴的垂线段PM、PN，垂足为M、N，所得矩形PMON的面积是___，周长是___。

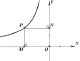
图6

在这样的教学设计中充分突出了知识点教学中的几个重点与难点：

1.在教学设计中的C点的坐标的几何意义得到了充分的解析，让同学们能更顺畅地理解矩形面积与|k|的内在联系。

2.通过列表、描点、动态轨迹演示的方法，能大大降低同学们在学习k的几何意义中存在的困惑，并且对反比例函数图像有了更深层次的理解。

3.在教学设计中由特殊到一般，由特殊矩形到任意矩形、由k= 12引导到k≠0的任意数、由第一象限扩展到所有象限，逐层递进为同学们的探究创造了层层阶梯，对于同学们的探究过程有着良好的引导作用。

4.在设计中自然而然地突出了在不同象限中对不同情况的思考，对于同学们进行分类思考，难点突破有着很好的作用。

5.本教学设计不是让同学在记忆公式的基础上进行解题训练，而是力求同学们在探究的过程中理解知识点之间的本质联系，在这个理解的基础上进行解题，在解题的过程中进一步理解知识点。并且对学有余力的同学设计了一些主动成长的机会。

6.这样设计的最大亮点也是与其他教学设计不同的地方是突出了同学们自主探究的过程，同学们在教师的引导下让同学们以小组为单位，通过独立思考、同伴互助、小组研讨的方式行进探究，对于知识点的内化有很好的支撑作用。

经过这样的逆向教学设计后，本人在所在学校进行了实践，在教学过程中明显感觉学生在这样的教学设计所营造的环境中同学们自主的探究过程得到了发挥，知识的内化过程也是顺其自然，可以说取得了非常好的教学效果。