解析图像，高效学习——初中数学“二次函数的图像与性质”教学探究

江苏省泰州市民兴实验中学初中部 曹晓梅

解析图像，高效学习
——初中数学“二次函数的图像与性质”教学探究

江苏省泰州市民兴实验中学初中部 曹晓梅

“二次函数的图像与性质”作为二次函数教学部分的基础知识，是学生解决相关数学问题的关键，重要性不言而喻。但是当前的课程教学方法却束缚了学生的思维，增加了学生理解的难度。本文就如何提升该部分数学知识的教学策略进行了探究，以期可以指导相关教学工作的开展。

初中数学；二次函数；图像；性质

直至今日，“函数热”依旧是当前初中数学教学的主要现状。但是由于二次函数等函数方面的知识具有较强的知识兼容性，对学生综合运用所学数学知识的能力要求比较高，学习起来难度比较大，所以其备受考试命题者的青睐。特别是图像和性质作为二次函数教学方面的重要基础知识，在提升学生函数解题方法方面具有重要意义。因此，对该部分数学知识进行教育具有重要的意义。

一、转变授课理念，奠定扎实基础

在现阶段的初中数学教学中，二次函数方面数学知识的授课主要安排在初三阶段。此时学生面临着中考的压力，并且课下的时间会被其他学科的作业所占据，这对数学教师的教学能力和学生的学习能力均有较高的要求。但是在这种授课背景下，大多数数学教师都会采用比较直白的授课方式，按照教材中的有关教学要求和顺序来照本宣科，即让学生先借助符号语言来了解二次函数所具有的性质，接着借助数学习题来强化学生对于这些基本的数学理论和图形知识的记忆后就草草了事。这种授课思路本着为后续中考复习留出足够复习时间的初衷是合理的，但是却因不合理的授课思路而影响学生灵活掌握和运用二次函数图像和性质方面知识来解决实际问题的效果。因此，在该部分数学知识的授课中，数学教师需要先转变自身的授课观念，采用引导式或者启发式等授课方式，以引发师生共鸣，切实突破该部分数学知识授课过程中存在的重难点知识。

此外，在该部分数学知识授课的过程中，为了帮助学生切实掌握该部分的数学知识，数学教师还需要重点地为学生讲解他们在学习过程中容易出错的教学内容以及他们在自主学习过程中的各种疑惑点，从而确保该部分数学知识授课的质量。例如，在该部分数学知识授课的过程中，数学教师大都先要求学生绘制y=2x2、y=2（x+1）2和y=2（x+1）2+3等几个二次项系数相同的函数，以引导学生自主归纳出y=a（x+m）2+K函数式的图像实际上可以借助y=a2这一函数进行平移得到，然后为学生归纳出了特定的平移方法。但是该种理解方法比较烦琐，学生很容易在学习过程中出现遗忘的现象，所以后续实际运用的过程中很容易出现差误。此时数学教师需要引导学生合理运用数形结合等方法来深化学生对于该部分数学知识的理解和认识，增强学生的学习效果。

二、明确授课思路，提升授课效率

为了帮助学生可以快速掌握该部分数学知识，数学教师需要先明确科学、合理的授课思路来充分调动学生学习的积极性，并要引导学生从多角度、多层次来观察二次函数图像所具有的各种数学性质，以使学生从亲自动手操作中感受和概括必要的数学知识。而就该部分数学知识具体的授课思路而言，其主要包括以下几个方面：首先，要绘制二次函数的标准图像，接着借助其来归纳出有关的数学性质。通常而言，相较于文本和符号语言而言，图形语言具有丰富的信息量，并且具有很强的直观性，同时也充分包含着数形结合的授课思想，所以在授课的过程中，数学教师需要充分利用图形语言来开展授课，以便达到增强授课效率的目的。具体主要是要求学生分别绘制出y=ax2和y=ax2+c、y=a（x-h）2+k、y=ax2+bx+c等形式的二次函数图像来让学生通过观察这些图像归纳和总结出二次函数图像及其所具有的各种数学性质。

其次，要做好数学性质的表述工作，并绘制相应的草图，以便学生通过亲自实践的绘制过程来更进一步地了解和掌握二次函数本身所具有的各种数学性质，同时借助学生绘制有关的函数图像，他们会深刻体会数与形二者之间具有的紧密关系。

最后，数学教师需要引导学生观察相关的二次函数图像，并求解出其相应的解析式，从而进一步使学生明确形与数之间的关系，增强学生学习的效果。例如，已知某二次函数的抛物线图像如图1所示，那么该二次函数解析式为？通过对该图像中抛物线的图形中的顶点坐标、对称轴及其同x轴的交点坐标，再加上二次函数图像的开口方向，则可以帮助学生采用待定系数法即可求解该道例题。如此一来，通过上述步骤的训练，学生会逐步掌握解决二次函数方面问题的方法。

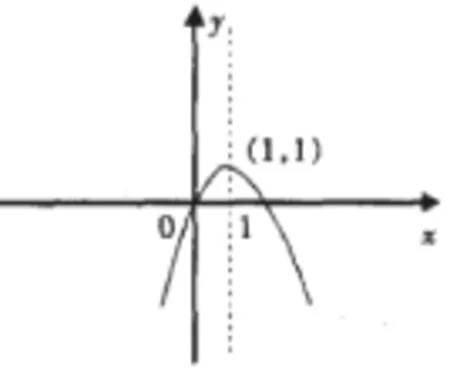
图1

三、传授解题方法，提升解题能力

俗话说：“授人以鱼不如授人以渔。”科学、合理的解题方法是提升学生解题质量和效率的重要途径，所以在讲解“二次函数图像与性质”这部分数学知识的时候，为了可以提升授课效果，提升学生解决实际函数问题的能力，数学教师必须运用一些常用的解题方法来帮助学生更好地解决有关的数学问题，从而不断提升学生的学习效果。比如，数形结合法是解决二次函数等函数方面问题的一个有效手段，数学教师需要重视该部分数学知识的讲解。例如，已知点（-1，y1）、（-3，y2）和（2，y3）等三个点均位于函数y=3x2+6x+2之上，那么三个未知参数的大小关系为：____。针对该道例题，学生可以先绘制出函数y=3x2+6x+2的图像，并将各个点标定出来，接着即可求直观得出有关的大小关系，具体图像如图2所示。

总之，教无定法。为了确保“二次函数的图像与性质”这部分数学知识的教学质量，数学教师必须要结合学生的实际学习情况，采用科学、合理的授课方法，同时教师也需要转变授课观念，明确授课思路，从而全面确保该部分授课工作的顺利进行。

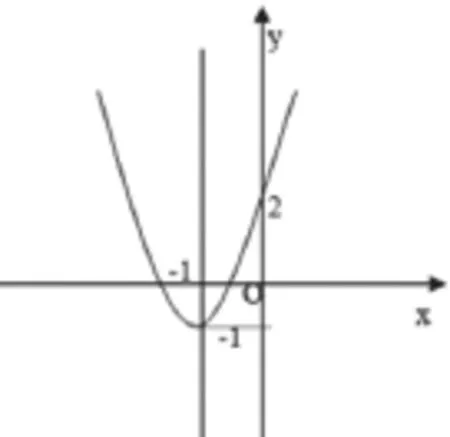
图2