从高考题出发浅析解析几何中的若干计算技巧

江苏省溧阳市埭头中学 蒋建荣

从高考题出发浅析解析几何中的若干计算技巧

江苏省溧阳市埭头中学 蒋建荣

圆锥曲线是解析几何的重要内容之一，而计算问题是学生解决圆锥曲线问题的一个难点，同时也是近年高考命题的热点和重点。学生在解决这类问题时，往往因为方法的选择而导致计算上的困难，因而形成难点。本文通过实例来说明解析几何中的计算问题的转化策略，归纳出解决这类问题的一些方法与技巧。

一、巧设直线，简化计算

若m=0，PC所在直线方程为：x=0，不符，舍

点评：以上方法利用直线过x轴上一点（c，0），则直线方程可设为x=my+c，大大简化了运算，特别是PC的求解很容易操作。

二、巧用弦长公式，简化计算

点评：弦长公式在解析几何平时的训练中经常会运用，是指直线截圆锥曲线所得弦长的一种简化解法。本题中PC虽然不是直线截椭圆所得，这个公式仍然使用。证明如下：

这样一来，我们就没有必要再去求PC所在直线方程及其yp，大大简化了计算。

这样的解题策略在2012江苏卷中已经出现过一次（2012江苏高考）。

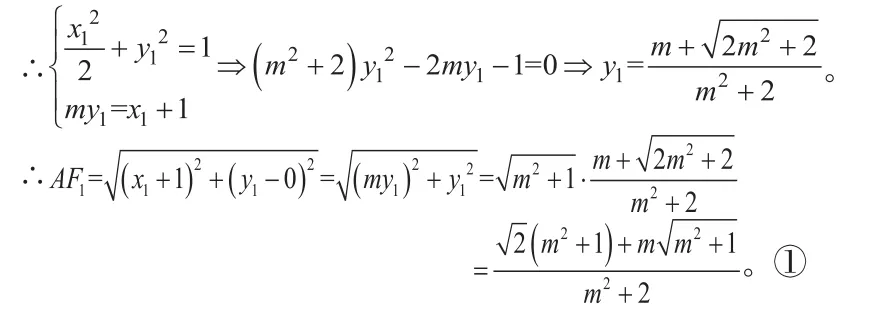
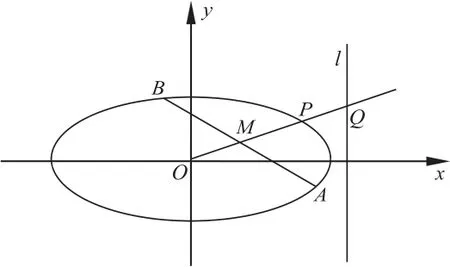
三、利用平面几何知识，简化计算

点评：解析几何问题离不开几何知识，本题利用相似三角形，将距离关系转化为坐标关系，极大地简化了计算，凸显了解析几何的特点：“用数研究形，以形助数”，这样的解题策略在模拟卷中已经出现过多次。

在解析几何的学习中，因为计算量大，运算复杂，使得很多的学生大伤脑筋，甚至望而却步。每年高考中失分的也不少，在解题中，尽量减少计算则成为迅速、准确地解题的关键。在求解时，一定要围绕解题目标，恰当地选择策略。在变中寻求不变，才能够有的放矢。