小议三角函数中的最值问题

福建省南安华侨中学高一（11） 彭江林

小议三角函数中的最值问题

福建省南安华侨中学高一（11） 彭江林

最值问题是中学数学的一个重要课题，它贯穿在中学数学的各个分支中。由于三角函数的特殊性质，因而三角函数的最值问题也灵活多样，成为考试、检查命题的一个热点。三角函数是一种重要的函数，三角函数的最值问题包括了对三角函数的概念、图像、性质及诱导公式、同角三角函数间基本关系式、两角和差以及倍角公式的考查，是函数思想的具体体现，有广泛的实际应用，一直是高考命题的热点。

解决三角函数最值问题，需以熟练掌握代数函数最值求法为基础，结合三角函数的特殊性质来解题。高中数学中，在分析三角函数问题时，比较常见的类型主要体现在以下几种类型，下面结合实例分析以下它们的解题策略：

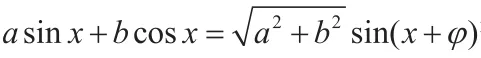
1.利用辅助角公式。

特点：一个分式，分子、分母分别会有正、余弦的一次式。几乎所有的分式型都可以通过分子、分母的化简，最后整理成这个形式，它的处理方式有多种。

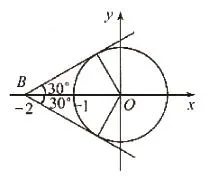
四、利用数形结合

五、利用基本不等式法

利用基本不等式求函数的最值，要合理的拆添项，凑常数，同时要注意等号成立的条件，否则会陷入误区。

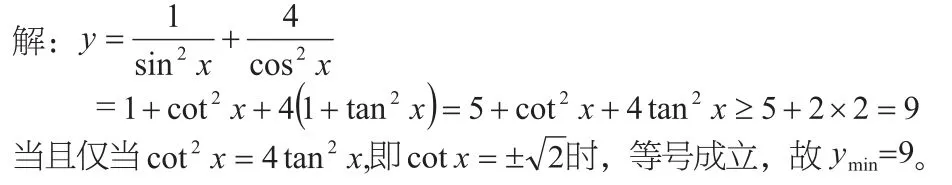
总之，三角函数求最值（或求值域）问题是具有典型性与综合性的函数求最值问题。以上几种方法中又以配方法和辅助角法及利用三角函数的有界性解题最为常见。解决这类问题最关键的在于对三角函数的灵活应用及抓住题目关键和本质所在。

（指导教师：王振阳）