雾的集合预报与集合预报的检验

杜钧 周斌斌

（美国国家海洋和大气管理局/美国国家环境预报中心，马里兰 20740）

雾的集合预报与集合预报的检验

杜钧 周斌斌

（美国国家海洋和大气管理局/美国国家环境预报中心，马里兰 20740）

简述了四部分内容：为什么要做雾的集合预报；雾的集合预报效果；其在目前业务数值预报中的应用情况及有待解决的问题；最后，介绍了集合预报的检验，读者可以从中体会集合预报的理念和优势。

雾，集合预报，集合预报检验

0　引言

本文作者参与了即将由Springer出版社出版的《海雾观测和预报进展及其面临的挑战》一书的编纂工作，负责撰写“雾的集合预报”一章[1]。鉴于集合方法在雾的预报上尚属开创阶段，许多问题有待探索，为让更多中文读者了解这一领域的进展，本文综述了该章的主要内容，主要从以下四个方面做了简要介绍。1）为什么要做雾的集合预报；2）雾的集合预报效果；3）其在业务数值预报中的应用情况，及有待解决的问题；4）集合预报检验。

考虑到集合预报的检验有别于通常单一确定预报的检验，许多读者不一定熟悉，所以关于集合预报的检验花了较多的笔墨。虽然篇幅仍短，但叙述尽量全面，这包括对集合成员、平均、离散度、概率和预报价值的检验，並尽量说明各检验方法背后隐藏的目的并指出它们的优缺点，以期读者可以通过本节讨论了解集合预报的理念及其优势。

1　为什么做雾的集合预报

过去十几年里，用数值模式尝试预报雾的努力愈来愈多。这包括一维的局地模式[2-5]和三维的数值预报模式[6-12]。但几乎所有这些努力都是确定预报而并不考虑预报的不确定性。对于一个非线性的数值天气预报模式，鉴于模式变量对初值和物理的敏感性[13]，用模式预报天气时集合方法是必需和科学的[14-17]。事实表明，雾对模式的初值和物理非常敏感[3,18-19]。许多人对这些敏感性进行了研究。

关于初值敏感性方面大致有四类工作：1）稍微改变初值。这类工作可用一维单个模式[3,18,20-22]，一维集合雾模式[5]和三维单一数值预报模式[6]。2）应用不同的分析场作为初值，如Pagowski等[9]。3）在初值中同化或不同化一些特殊的观测资料，可用一维[3]和三维模式[23]。4）利用集合数值预报模式系统，如Zhou等[24]和Hu等[25]的工作。以上这些工作都表明雾的生成、时间和地点的预报对模式低层的水汽、云覆盖、位温和风等初值很敏感。

模式的敏感性，主要源自对次网格尺度物理过程描述的不确定性，所以雾预报对参数化物理，如对流、微物理、行星边界层、地面层、辐射和陆面过程（包括陆、水、冰雪圈）等很敏感。这些参数化物理往往导致模式低层的水汽场、温度场出现系统性偏差，进而导致雾预报的失败。与微物理有关的工作有Zhang等[26]、Steeneveld等[27]、Kim等[28]、Ryerson等[29]、Kunkel[30]、Stolinga等[31]以及Gultepe等[32]的工作。与行星边界层有关的工作有Li等[33]和Roman-Cascon等[34]的工作。Gultepe等[35]和Koracin等[36]对这方面有详细的总结。相较初值，雾对物理过程的敏感性研究工作较少，如对对流参数化方案的敏感性工作尚未见。

雾预报除了对初值和物理敏感之外，对模式的分辨率[4,6,37-38]、植被[39-40]、地表、地形[41]和雾的诊断方案[24]等都很敏感。所以，如仅用单一模式的单一解来提供确定性的雾预报是不科学的，有很大的随机性。而这种预报的不确定性必需要用集合预报的方法来进行定量化以便用户更科学地决策[16,42]。

2　雾的集合预报效果

Zhou等[24]曾利用2008年北京夏季奥运会天气预报示范项目[43]中美国国家环境预报中心（NCEP）的中尺度集合预报系统对中国东部13个城市在2008年2—9月逐日一次进行了雾的实时预报试验。此中尺度集合系统是NCEP业务短期集合预报系统（SREF）[44]的一个简化版，用了WRF-NMM和WEF-ARW两个模式，有10个成员（每个模式各5个）。该研究发现集合方法既可明显改进确定性的雾预报，更可提供能定量描述预报可信度（或预报不确定性）的概率预报。

图1是单一控制预报和几个基于集合成员的中值预报（对应概率50%的预报①但由于该集合系统中针对某一模式只有5个成员，所以只能用对应40%的预报来代替。）的ETS（Equitable Threat Score）评分。ETS是衡量预报同观测范围重合、空报和漏报程度的综合指标。预报雾发生与否的具体诊断方案是“雾的多重规则诊断法”[见文献1, 24, 45]。图1表明仅仅用单一模式的控制预报（Ctl）其ETS为0.192，而用单一模式5个成员的集合中值预报（SM5）则可提高17.2%，使ETS达到0.225。集合技术和集合成员数对预报技巧的提高也很关键，如用两个模式但仍保持5个成员的集合中值预报（MM5）可把ETS从0.225提高到0.264（提高17.3%）；再把成员数增加到10（MM10），则ETS又可从0.264增加到0.334（提高26.5%）。所以，集合方法可明显地（比原单一控制预报提高74.0%）改进雾发生与否的预报。

集合预报不仅仅可以提高确定性单一预报的技巧，更重要的是可得到概率预报从而对预报的可信度或预报的不确定性做出定量的估计。同基于统计方法的概率预报不同，基于动力集合模式的概率预报可直接反映当时大气的可预报性，而不是统计意义上的平均情况。这对如何利用天气预报信息来科学地决策具有重大的经济价值[42]。该研究表明无论是基于单一模式集合系统还是多模式集合系统，它们的概率预报都比原来单一控制预报含有更多的预报信息（可参考文献[1]中的图4）。

注意，当集合成员数达到一定数量后，预报技巧的提高会逐渐趋于饱和，关于这方面的讨论可见文献[17, 46]。如Richardson[47]的研究表明，集合成员数较少时（＜10），概率评分会明显随成员数的增加而提高（这对可预报性较低的事件更是如此），但当成员数较大时（＞50），概率评分趋于饱和。所以，要获得稳定可靠的概率预报，集合成员数不能太少，应为10～50。

其次，要监督中标单位严格执行投标书中的实施方案，如果私自修改施工方案，必须进行返工处理；如果进度、质量等不能满足要求，必须进行整改并提交罚款。

3　在业务数值预报中的应用情况

在美国国家环境预报中心，用集合系统尝试预报雾和低能见度（≤1000m）始于2004年[48-50]。把雾的诊断方案直接放在一日运行4次的短期集合预报系统SREF模式的后处理程序中，由每个集合成员分别输出各自的雾预报。后来为了航空预报的需要，又把雾和低能见度的预报引入到基于13km分辨率、每小时更新的“北美快速变换模式”和利用时间滞后法（外加12km NAM模式）建立的集合产品（NARRE-TL）中[51-52]。最近又把雾和低能见度预报引入到了3～4km的高精度模式时间滞后集合产品中（HREF-TL）。雾的诊断方案最先是用模式最低层含水量来表示，然后发展为“多重规则诊断法”，为了进一步预报雾的强度又发展了“物理过程平衡法”，这些方法的详细介绍可见文献[1]和[45]。另外，我们的试验表明，直接基于雾的诊断方案比用基于能见度的间接方法（≤1000m定义为雾）来预测雾要更准确。

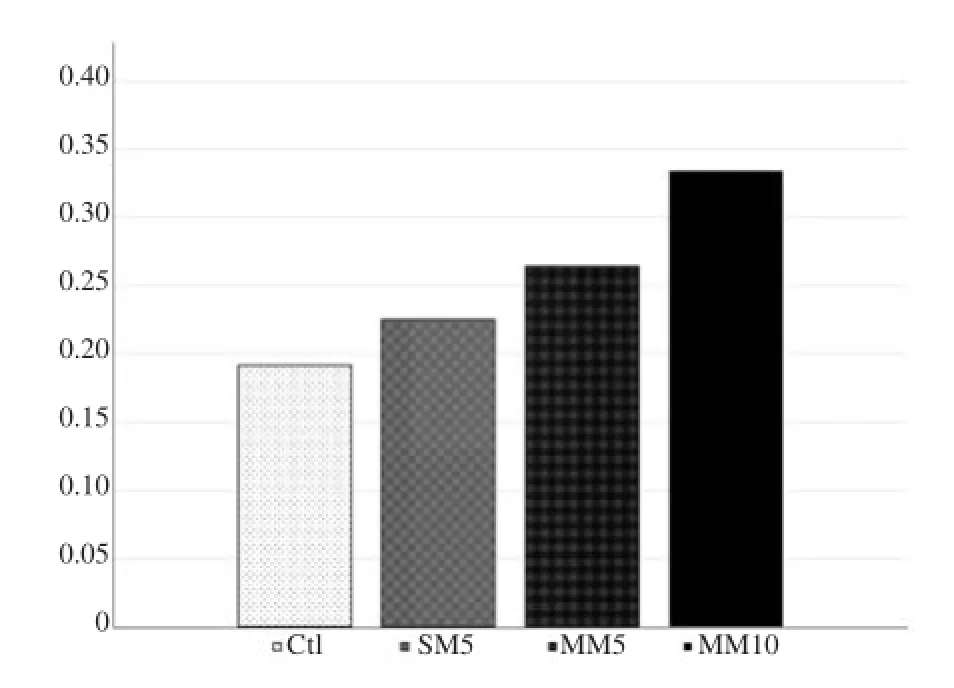
图1　各种雾预报的ETS评分（Ctl：控制预报；SM5：基于5个成员单一模式集合系统的中值预报；MM5：基于5个成员多模式集合系统的中值预报；MM10：基于10个成员多模式集合系统的中值预报。由于针对某一模式只有5个成员，这里中值预报对应的概率用40%而不是50%）Fig. 1 ETS scores from the various forecasts （Ctl： the single control runs （0.192）； SM5： the 40% probability forecasts based on the 5-member single-model ensembles （0.225）； MM5： the 40% probability forecast based on the 5-member （3 NMM and 2 ARW） multi-model ensemble （0.264）， and MM10： the 40% probability forecast based on the10-member （5 NMM and 5 ARW） multimodel ensemble （0.334）

制作的集合预报产品有三大类：集合平均、集合离散度和概率预报。由于非线性的过滤作用，集合平均把低可预报性的部分（集合成员间信息不一致的地方）过滤掉了，所以集合平均和中值可以看作统计上最有可能出现的解（但不适用于降水这一类非正态分布的要素）。集合离散度可以看作是对集合平均预报不确定性的度量。而概率是对某一特定事件预报可信度的衡量。另一类较常用的产品是聚类，这在大气有多平衡态倾向时，可有效地反映大气的多种可能解。

总的说来，目前直接用数值预报模式来预报雾和低能见度的能力还很低。如2014年9月NCEP两个区域模式（12km的NAM和13km的RAP）单一控制预报对低能见度（≤1000m）预报的平均ETS分别为0.07和0.125。但用集合方法可以提高其准确性，如其对应的NARRE-TL集合平均预报ETS为0.15，这比NAM的控制预报提高了50%，比RAP的控制预报提高了20%，但它仍比当前降水预报平均水平（ETS为0.35左右）低很多。基于NARRE-TL的低能见度事件的概率预报也比两个控制预报（NAM和RAP）更有技巧、含有更多的信息。

除了NCEP外，美国空军气象局也在业务上用中尺度集合预报系统来预报雾[53-54]。法国戴高乐机场在业务上也用一维雾模式的集合预报系统（30个成员）来预报机场的雾[5,55-56]。它们都比原来单一模式预报有所改进。然而，雾的集合预报技术目前还不成熟，因为数值预报中心的集合预报系统往往是为一般天气预报建立的，其初值扰动和物理扰动技术是否适合于雾的预报有待验证。釆用多种雾诊断方案的集合也是一种可以尝试的方法。雾的集合预报产品和针对雾的集合平均、离散度和概率的后处理订正等工作还有待开展。

4　集合预报系统的检验

衡量一个集合预报系统的优劣不同于衡量单一确定预报，仅仅检验预报的准确性并不能说明该集合系统的优劣，如集合系统A的集合平均预报准确性比集合系统B的高并不能说明系统A优于系统B，而只能说明用于系统A的模式优于系统B的模式。下面罗列一些衡量一个集合系统好坏的指标和方法。

4.1集合成员

一个好的集合预报系统，要保证集合成员“表现同等性”和成员之间的“信息独立性”。前者是说从统计平均来看，每个集合成员的预报准确性应大致相同，否则表现总是较差的成员可以去掉。这一特性常用“表现同等性”的直方图（Equally-likely Histogram）来衡量，它表示每个成员最接近实况的机率（%），这可以通过对所有预报空间点（如模式格点）和大量样本进行统计得到。表现同等性是从统计平均意义上说的，但对某一具体预报，成员并不一样准确而有好坏之别，对成员好坏的排序预测方法见文献[57]。后者是说，在预报不确定性空间上，每个成员之间的信息要尽量独立，这样可以使整个集合所包括的信息达到最大化，即每个成员可以弥补其他成员之不足，从而描绘出一幅最完整的图画。反之，如果每个成员都提供一样的信息（除非单一预报100%准确，预报没有不确定性，这种情况才正常），那么一个成员的单一预报就够了。关于成员间独立性的检验，可用成员扰动场间的相似度（如相关系数）和集合预报的信息度（information content）来衡量。信息独立性同可预报性有关（见后面集合离散度的检验），对于可预报性很高的大气状态，集合成员应该较一致，反之较不一致。另外，信息独立性要在保证表现同等性的前提下来实现，而不以降低个别成员预报准确性为代价。对于多模式集合系统，由于模式之间差距较大，要实现成员间表现同等性较不易。

4.2集合平均

由于集合平均过程的非线性过滤作用，集合平均从统计上来说应是最好的预报，要优于任一集合成员。所以，一个好的集合预报系统要具有这一特性，这可用任何常规检验确定预报的方法如均方根误差、相关系数和ETS等来检验。注意，这一标准一般仅可用在具有正态分布的变量上，而不能用在具有明显单边分布的场，如降水预报。由于平均的光滑作用，集合平均会使弱降水区域扩大而强降水区域缩小，导致集合平均降水，特别是大量级的降水预报比集合成员更差。为了解决这一问题，概率（或频率）匹配集合平均法应该用在降水这一类的预报量上，而不能用简单的算术平均，杜钧等[17]对此有详细的讨论。平均过程的光滑作用会使集合平均场失去细小的结构，减少其在空间上的变率等，这些都是集合平均带来的一些副作用。

4.3集合离散度

集合预报的主要目的并不是仅仅要提高单一确定预报的准确性，更重要和更难的是定量估计一个预报的可信度或预报的不确定性[16]，用集合离散度来模似预报误差的可能分布。所以离散度大小要反映大气的可预报性：可预报性高时离散度就小，可预报性低时离散度就大，这是衡量一个集合预报系统好坏的关键。以下是几种目前常用的离散度检验方法。一是集合平均预报的均方根误差同集合离散度（成员预报相对集合平均的标准差）相比较（图2a—2c），如果离散度大于、小于或等于预报均方根误差，则分别表明集合系统离散度太大、太小和适当。有时又把均方根误差同离散度的比值（RMSE/Spread）称之为误差—离散度一致性，简称“一致性（consistency）”（图2d—2f），所以当一致性的值小于、大于或等于1.0时，分别对应为集合离散度太大、太小和适当的情形。注意，如果预报有很大的系统性偏差，均方根误差（RMSE）就会很大，但这並不反映真正的可预报性（由不可预报性所产生的误差是随机误差，系统性误差是由模式或初值的缺陷所造成的），这时就会产生虚假的集合离散度不够大的现象。因此，在检验离散度时，要先订正预报的系统性偏差。但是，即使在没有系统性偏差的情况下，这一检验方法也有可能误导：由于这个度量往往是一个区域的平均值，它仅反映整个区域的平均情况，而并不反映局地小区域的情况。如RMSE有可能被局部地区个别特大的误差所主导，而导致集合离散度在整个区域不够大的虚假现象。

另一常用的检验离散度的方法是Talagrand分布[58]或分级直方图（图3）。对任一预报时刻的任一空间点，把n个集合成员的预报值从左到右按由小到大的次序排列形成n+1个区间，然后对大量空间点统计出实况出现在每一区间内的频率，其中最左边（最右边）的单边区间表示实况比最小（最大）的成员还要小（大），即超出集合预报范围。如前所述，对一个完美的集合预报系统，从统计平均的角度来说，其任一成员都有同样的可能性代表实况，或说实况有相同的机率落入任一区间。所以，如果直方图成平直分布（图3a），则表明完美的离散度，如成U状（倒U状）分布，则表明离散度太小（太大）（图3b和3c），如成L（或反L）分布，则表明预报有系统性正（负）偏差（图3d和3e）。因为最左（右）边的直方柱表示实况小于（大于）任一集合成员的机率，这两极之和则为实况出界（即没被集合预报范围所包括）的机率，定义为“出界率（outlier）”。出界率应该随着集合成员数的增多而减少，对一个具有完美平直Talagrand分布的集合预报系统而言，理论上出界率的期望值应该是1/(n+1)的两倍。

图2　检验集合离散度的方法之一：同集合平均预报误差相比较（a）—（c）：离散度（Spread，虚线）直接同预报的RMSE（实线）相比较；（d）—（f）：一致性（RMSE/Spread）Fig. 2 Quality measure of ensemble spread（a） — （c）： Comparison of ensemble spread （dash line） to the RMSE of ensemble mean forecast （solid line）； （d） — （f）：Consistency （the ratio of RMSE to spread）

另外，因为集合预报的离散度是集合平均预报误差的预估，离散度分布和集合平均预报绝对误差分布之间应有高的正相关，称之为“离散度—预报技巧”关系[59]。从总体统计的角度，人们常用离散度与预报均方根或绝对误差两者相比较的点聚图来表征，把某一区域内所有空间点上的离散度与预报误差这一对数值点画在一起来检验它们之间是否有正相关，即离散度小（大）时，预报误差较小（大）。实际情况表明，这一关系在离散度的两端较明显，即离散度很小时预报误差也小，离散度很大时预报误差也较大；但在离散度的中间段这一关系并不明显，对应的预报误差大小不一、变化范围很大。从空间分布角度，可计算离散度分布和集合平均预报绝对误差分布之间的空间相关，相关越高，表明集合离散度模拟预报误差的能力越强。在目前的业务集合预报系统中，这一离散度—预报技巧关系尚不太理想。以上离散度—预报技巧关系的检验是相对集合平均预报而言的，另外也有考虑同集合成员的关系为出发点的方法，如把离散度大小同集合成员误差变化范围大小相联系[60-61]。一般而言，离散度小（大）时，成员间预报误差变化范围较小（大）。

4.4概率预报

基于集合预报的概率是对某一确定预报可信度的度量。检验概率值本身大小是否有意义，其衡量的指标是可靠性（reliability）和分辨率（resolution）。可靠性是衡量预报的概率同该概率相对应的实况所出现的频率两者是否一致。完全可靠的预报概率应该同实况出现的频率一致，如预报70%，则该事件在实况中的应验率也该是70%。因此，检验概率预报需要大量的样本。概率预报的可靠性是用户科学决策的关键[42]。分辨率是预报概率同气候概率的差异，是衡量一个预报概率值含有的预报信息量，分辨率愈高，概率预报愈有信息。虽然气候概率是完全可靠的，但却没有分辨率。如果一个预报概率等同于气候概率，那么就等同于在所有过去天气样本中随机取样一般，没有可预报性。因此，一个好的集合预报系统所产生的预报概率，在保证其可靠性的前提下，要尽量提高概率值的分辨率。

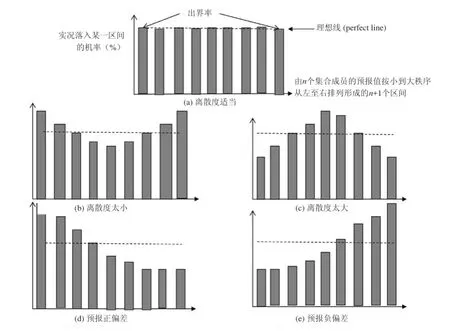
图3　检验集合离散度方法之二：Talagrand分布或分级直方图（图中水平虚线表示1/（n+1）值）（a）离散度适当；（b）离散度太小；（c）离散度太大；（d）预报正偏差；（e）预报负偏差Fig. 3 Talagrand Distribution or Ranked Histogram for measuring ensemble spread quality： （a） perfect spread， （b） under dispersion， （c） over dispersion， （d） positive bias， and （e） negative bias. Horizontal dash line indicates the value of 1/（n+1）

检验一个概率预报同实况的关系时有两种做法。其一是直接用概率表达，譬如明晨出现浓雾的概率是85%。这时概率值越大就表示发生的可能性越高，同实况（100%）越接近。BS（Brier score）和RPS（ranked probability score）或CRPS（continuousranked probability score）这几种评分就是用来检验这类概率预报的（BS是针对单一类事件，而RPS或CRPS是针对连续分类的多事件的）。另一种做法是把概率预报转变为单一的确定预报，有如下两种转换法：一是针对某一天气事件，如能见度小于1km，事先确定一个概率阈值（如50%，90%等），把符合阈值规定的概率预报定义为“有”，反之为“无”的二分类预报。基于二分类预报的列联表（contingency）表（由命中率、漏报率、空报率和正确排除率四项组成），可计算“相对运行特性曲线”（relative operating characteristic或receiver operating characteristic curve，ROC），ROC曲线由命中率（垂直y轴）相对空报率（水平x轴）组成，用ROC曲线下方同x轴和y轴所围成的面积大小来衡量该预报的技巧，面积越大，预报越有技巧，ROC曲线是描述概率预报分辨率的。二是根据用户对天气的依赖程度，先决定一概率值，如50%，再产生同此概率相对应的具体预报值，如同50%概率相对应的即为集合的中值预报。同理，用户可以产生10%和90%等预报。检验这类预报的评分同检验单一确定预报如上述的集合平均预报是一样的，可用均方根误差、相关系数、TS评分等。关于概率预报的检验，可进一步参考文献[62-63]。

4.5预报的价值

基于二分类预报的列联表再加上某一天气事件发生的气候概率，可进一步计算该预报对不同用户（风险与利益比）的“相对经济价值”大小。实际计算表明，基于集合概率的预报比单一确定预报更有价值，并适用于从低风险到高风险更广泛的用户。关于相对经济价值的计算和意义可参阅文献[42, 64]。

5　小结

雾的预报对模式初值和物理方案等非常敏感，因此在雾的数值预报中釆用集合方法是必需的和科学的。集合方法不但能提高单一确定预报的准确性，更重要的是可定量估计预报的可信度，以供用户更好地科学决策。虽然雾的数值预报已在业务中开始应用，但它的技巧还不高（远比模式降水预报差），这可能是针对雾的物理过程在模式中的描述还不理想（一般数值模式并不是专门针对雾的，而是针对其他一般的天气现象）。

集合预报的检验不同于单一确定预报的检验，它更侧重于集合离散度和概率预报的检验，同时还要综合考虑集合平均预报和每个集合成员的预报。一般而言，基于集合的各类预报比单一确定预报更有价值，并适合更多的用户。

［1］ Du J， Zhou B. Ensemble fog prediction// Koračin D， Dorman C. Marine Fog - Challenges and Advancements in Observations and Forecasting. Berlin： Springer， 2016.

［2］Bott A， Trautmann T. PAFOG- a new efficient forecast model of radiation fog and low-level stratiform clouds. Atmos Res， 2002， 64：1-4， 191-203.

［3］Bergot T， Carrer， Noilhan J， et al. Improved site-specific numerical prediction of fog and low clouds. A feasibility study. Wea Forecasting， 2005， 20： 627-646.

［4］Bergot T， Terradellas E， Cuxart J et al. Intercomparison of singlecolumn numerical models for the prediction of radiation fog. J Appl Meteor and Clim， 2007， 46： 504-521.

［5］Roquelaure S， Bergot T. A Local Ensemble Prediction System（L-EPS） for fog and low clouds： construction， Bayesian Model Averaging calibration and validation. J Appl Meteor and Clim. 2008，47： 3072-3088.

［6］Ballard S P， Golding B W， Smith R N B. Mesoscale model experimental forecasts of the Haar of Northeast Scotland. Mon Wea Rev， 1991， 119： 2107-2123.

［7］Teixeira J. Simulation of fog and mist. Quart J Roy Meteor Soc，1999， 125： 529-553.

［8］Kong F. An experimental simulation of a coastal fog-stratus case using COAMPS model. Atmos Res， 2002， 64： 205-215.

［9］Pagowski M， Gultepe I， King P. Analysis and modeling of an extremely dense fog event in southern Ontario. J Appl Meteor， 2004，43： 3-16.

［10］Koracin D， Businger J A， Dorman C E， et al. Formation， evolution，and dissipation of coastal sea fog. Boundary-Layer Meteor， 2005，117： 447-478.

［11］Muller M D. Numerical simulation of fog and radiation in complex terrain. Basel： University of Basel， 2005.

［12］Gao S， Lin H， Shen B， et al. A heavy sea fog event over yellow sea in March 2005： analysis and numerical modeling. Adv Atmos Sci，2007， 24 （1）： 65-81.

［13］Lorenz E N. A study of the predictability of a 28-variable atmospheric model. Tellus， 1965， 17： 321-333.

［14］Leith C E. Theoretical skill of Monte Carlo forecasts. Mon Wea Rev， 1974， 102： 409-418.

［15］Du J. Uncertainty and ensemble forecasting. NOAA/NWS Science and Technology Infusion Lecture Series， 2007. http：//www.nws. noaa.gov/ost/climate/STIP/uncertainty.htm.

［16］杜钧， 陈静. 单一值预报向概率预报转变的基础： 谈谈集合预报及其带来的变革. 气象， 2010， 36（11）： 1-11.

［17］杜钧， 李俊. 集合预报方法在暴雨研究和预报中的应用. 气象科技进展， 2014， 4（5）： 6-20.

［18］Bergot T， Guedalia D. Numerical forecasting of radiation fog. Part I： numerical model and sensitivity tests. Mon Wea Rev， 1994， 122：1218-1230.

［19］Gayno G A. Development of a higher-order， fog producing boundary layer model suitable for use in numerical weather prediction. State College： The Pennsylvania State University， 1994.

［20］Musson-Genon L. Numerical simulation of a fog event with a one-dimensional boundary layer model. Mon Wea Review， 1987，115： 592-607.

［21］Fitzjarrald D R， Lala G G. Hudson Valley fog environment. J Appl Meteor， 1990， 28： 1303-1328.

［22］Guedalia D， Bergot T. Numerical forecasting of radiation fog. Part II： a comparison of model simulation with several observed fog events. Mon Wea Rev， 1994， 122： 1231-1246.

［23］Wang Y， Gao S， Fu G， et al. Assimilating MTSAT-derived humidity in nowcasting sea fog over the Yellow Sea. Wea and Forecasting， 2014， 29： 205-225.

［24］Zhou B， Du J. Fog prediction from a multimodel mesoscale ensemble prediction system. Wea and Forecasting， 2010， 25：303-322.

［25］Hu H ， Zhang Q， Xie B， et al. Predictability of an Advection Fog event over North Chia. Part I： sensitivity to initial conditiondifferences. Mon Wea Rev， 2014， 142： 1803-1822.

［26］Zhang X， Musson-Genon L， Dupont E， et al. One the influence of a simple microphysics parameterization on radiation fog modeling：a case study during Paris Fog. Boundar-Lay Meteor， 2014， 151：293-315.

［27］Steeneveld G J， Ronda R J， Holtslag A A M. The challenge of forecasting the onset and development of radiation fog using mesoscale atmospheric models. Boundary-Lay Meteor， 2015， 154：265-289.

［28］ Kim C K，Stuefer M， Schmitt C G， et al. Numerical modeling of ice fog in interior Alaska using the weather research and forecasting model. Pure Appl Geophys， 2014， 171： 1963-1982.

［29］ Ryerson W R， Hacker J P. The potential for mesoscale visibility prediction with a multimodel ensemble. Wea and Forecasting，2014， 29： 543-562.

［30］Kunkel B A. Parameterization of droplet terminal velocity and extinction coefficient in fog models. J Climate Appl Meteor， 1984，23： 34-41.

［31］Stoelinga M T， Warner T T. Nonhydrostatic， mesobeta-scale model simulations of cloud ceiling and visibility for an east coast winter precipitation event. J Apply Meteor， 1999， 38： 385-404.

［32］Gultepe I， Muller M D， Boybeyi Z. A new visibility parameterization for warm-fog application in numerical models. J Appl Meteor and Clim， 2006， 45： 1469-1480.

［33］Li Y， Zheng Y. A analysis on atmospheric turbulence near the top layer of sea fog. Chines J of Ocean and Lim， 2015. doi： 10.1007/ s00343-015-4030-0.

［34］Roman-Cascon C， Yague C， Sastre M， et al. Observations and WRF simulations of fog events at the Spanish Northern Plateau. Adv Sci Res， 2012， 8： 11-18.

［35］Gultepe I， et al. Fog research： a review of past achievements and future perspectives. Pure and Applied Geophysics， 2007， 164：1420-9136.

［36］Koracin D， et al. Marine fog： a review. Atmos Res， 2014，143：142-175.

［37］Tardif R. The impact of vertical resolution in the explicit numerical forecasting of radiation fog： a case study. Pure and Applied Geophysics， 2007， 164： 1221-1240.

［38］Van der Velde I， Steeneveld G， Wichers Schreur B， et al. Modeling and forecasting the onset and duration of severe radiation fog under frost conditions. Mon Wea Rev， 2010， 138： 4237-4253.

［39］Glasow R V， Bott A. Interaction of radiation fog with tall vegetation. Atmos Environ， 1999， 33： 1333-1346.

［40］Fedorova N， Levit V， Souza J L. Fog events at the Maceio Airport on the northern coast of Brazil during five years 2002-2005. Pure and Applied Geophysics， 2015， doi： 10.1007/s00024-014-1027-0.

［41］Golding B W.A study of the influence of terrain on fog development. Mon Wea Rev， 1993，121： 2529-2541.

［42］杜钧， 邓国. 单一值预报向概率预报转变的价值： 谈谈概率预报的检验和应用. 气象， 2010， 36（12）： 10-18.

［43］Duan Y H， Gong J， Du J， et al. An overview of the Beijing 2008 Olympics Research and Development Project （B08RDP）. Bull Amer Meteor Soc， 2012， 93： 381-403.

［44］Du J， DiMego G， Toth Z， et al. NCEP short-range ensemble forecast （SREF） system upgrade in 2009. 19th Conf on Numerical Weather Prediction and 23rd Conf on Weather Analysis and Forecasting， Omaha， Nebraska， Amer Meteor Soc， June 1-5， 2009. http：//www.emc.ncep.noaa.gov/mmb/SREF/reference.html.

［45］周斌斌， 蒋乐， 杜钧. 航空气象要素以及基于数值模式的低能见度和雾的预报. 气象科技进展， 2016， 6（2）： 29-41.

［46］Du J， Mullen S L， Sanders F. Short-range ensemble forecasting of quantitative precipitation. Mon Wea Rev， 1997， 125： 2427-2459.

［47］Richardson D S. Measures of skill and value of ensemble prediction systems， their interrelationship and the effect of ensemble size. Quart J Royal Meteor Soc， 2001， 127： 2473-2489.

［48］Zhou B， et al. An Introduction to NCEP SREF Aviation Project. 11th Conference on Aviation， Range， and Aerospace， Hyannis， Oct 4-8， 2004. Amer Meteor Soc， 2007.

［49］Zhou B， Du J， Ferrier B S， et al. Numerical forecast of fog： central solutions. 18th Conference on Numerical Weather Prediction， Park City， Utah， June 25-29， 2007. Amer Meteor Soc， 2007.

［50］Zhou B， Du J， Gultepe I， et al. Forecast of low visibility and fog from NCEP： current status and efforts. Pure and Applied Geophysics， 2012， 169： 895-909.

［51］Zhou B， Du J， DiMego G. Introduction to the NCEP Very Short Range Ensemble Forecast System （VSREF）. 14th Conf. on Aviation， Range， and Aerospace， 90th AMS Annual Meeting，Atlanta， GA， January 17-21， 2010.

［52］Zhou B， Du J， Manikin G， et al. Introduction to NCEP's time lagged North American Rapid Refresh Ensemble Forecast System（NARRE-TL）. Conference on Aviation Range and Aerospace Meteorology， Amer Meteor Soc， CA， Los Angles， 2011.

［53］Hacker J， et al. The U.S. Air Force Weather Agency's mesoscale ensemble： scientific description and performance results. Tellus，2011， 63A： 625-641.

［54］ Ryerson W R. Toward improving short-range fog prediction in data-denied areas using the Air Force Weather Agency mesoscale ensemble. Monterey： Naval Postgraduate School， 2012.

［55］Roquelaure S， Bergot T. Contributions from a Local Ensemble Prediction System （LEPS） for improving fog and low cloud forecasts at airports. Wea and Forecasting， 2009， 24： 39-52.

［56］Roquelaure S， Bergot T. Skill of a ceiling and visibility Local Ensemble Prediction System （LEPS） according to fogtype prediction at Paris-Charles de Gaulle Airport. Wea and Forecasting， 2009， 24： 1511-1523.

［57］Du J， Zhou B. A dynamical performance-ranking method for predicting individual ensemble member performance and its application to ensemble averaging. Mon Wea Rev， 2011， 139：3284-3303.

［58］Talagrand O， Vautard R， Strauss B. Evaluation of probabilistic prediction systems. Proceedings， ECMWF Workshop on Predictability， Shinfield Park， Reading， 20-22， October， 1997

［59］Whitaker J S， Loughe A F. The relationship between ensemble spread and ensemble mean skill. Mon Wea Rev， 1998， 126：3292-3302.

［60］Grimit E P， Mass C. F. Measuring the ensemble spread-error relationship with a probabilistic approach： stochastic ensemble results. Mon Wea Rev， 2007， 135： 203-221.

［61］Du J. New metrics for evaluating ensemble spread. 21st Conf on Probability and Statistics in the Atmospheric Sciences，92nd AMS Annual Meeting， New Orleans， LA， Jan 22-26，2012. https：//ams.confex.com/ams/92Annual/flvgateway.cgi/ id/20391？recordingid=20391.

［62］Wilks D S. Statistical Methods in Atmospheric Sciences， 2nd Ed.// International Geophysics Series， Vol. 59. Academic Press，2006.

［63］Toth Z， Talagrand O， Candille G， et al. Probability and Ensemble Forecasts I// Jolliffe T， Stephenson D B. Forecast Verification. West Sussex： Wiley Press， 2003.

［64］Richardson D S. Skill and relative economic value of the ECMWF ensemble prediction system. Quart J Royal Meteor Soc， 2000， 126：649-668.

Ensemble Fog Prediction and Ensemble Forecast Verification

Du Jun, Zhou Binbin
（Environmental Modeling Center， NCEP/NWS/NOAA， College Park， MD 20740）

This paper discusses the following four aspects: why do we need an ensemble approach in predicting fog? What improvements have been seen through an ensemble approach? What are the status and challenges of fog ensemble prediction in current numerical weather prediction operation? The verification of ensemble forecasts is also introduced to help readers understand and appreciate the ensemble approach.

fog， ensemble prediction， ensemble forecast verification

10.3969/j.issn.2095-1973.2016.03.005

2016年2月2日；

2016年4月1日

杜钧（1962—），Email: jundu_noaa@yahoo.com