兰勃特投影与高斯投影的正解析变换研究
张健雄,李亚磊
(河南理工大学 测绘与国土信息学院,河南 焦作454003)
兰勃特投影与高斯投影的正解析变换研究
张健雄,李亚磊
(河南理工大学 测绘与国土信息学院,河南 焦作454003)
兰勃特投影和高斯投影是我国常用的两种等角投影,两者之间的坐标转换是实际应用中常见的基本问题。文章针对目前使用的反解析变换法计算解决复杂及正解析变换法精度偏低的问题,采用Mathematica数学软件对正解析变换公式重新推导,得出坐标变换公式,经验证,在4°(纬差)6°(经差)的转换区域精度达到1mm,能够满足测量和制图精度要求。
高斯投影;兰勃特投影;解析变换法;转换精度
高斯投影和兰勃特投影是常用的两种等角投影,广泛用作地图制作。国家基本比例尺地形图采用的是高斯克吕格投影,1:100万地形图和航空图采用的是兰勃特等角圆锥投影[1]。根据投影变形规律差异,高斯投影适用于南北长而东西狭窄的区域,兰勃特投影适用于东西长而南北狭窄的区域,因此在实际应用中两者之间的相互转换是常见的基本问题。变换的主要方法有解析法和数值法,其中解析法最为常用,它又分为正解析法与反解析法[2-4]。反解析法是利用大地坐标作为过渡,采用(xG,yG)(B,l)(xL,yL)的方式进行转换。这种转换方式理论严密,严格意义上无精度损失,且不受转换区域范围限制;缺点是计算量大,过程复杂[5-6]。正解析法是根据复变函数理论,将两种投影变换公式在某点处作级数展开,通过将一种投影坐标展为另一种投影坐标级数的形式实现坐标转换。正解析法无需任何中间变量,可直接实现两种投影间坐标转换,不足之处是这种转换方式精度受展开阶数限制,在转换范围过大时精度偏低。本文在前人研究成果的基础上,改进正解析法公式推导方式,采用Mathematical计算软件对转换公式进行重新推导,得到较高的转换精度。
1 兰勃特平面坐标与高斯平面坐标的正解析换算
由于这两种投影都是等角投影,所以两种坐标之间存在一个复变函数的关系[7, 8]。设x,y为兰勃特投影上某一点的平面直角坐标,x`,y`为高斯克吕格投影上相当点的坐标,则这个函数关系为:
x`+iy`=f(x+iy)
(1)
将式(1)右边的函数展为麦克劳伦级数,则得:
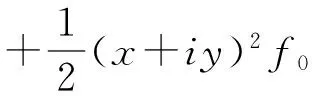
(2)
式中:f0表示函数f0(x+iy);f`0、f″0分别为f0函数关于x+iy的一阶、二阶导数,下标0表示这个函数和各导数都须归算为零点之上,即归算到x=0及y=0之上。求得各阶导数值即可得两种投影间的解析换算公式。
由于兰勃特投影上中央经线的选择是不受任何限制的,故可以假定这两种投影都是以同一经度的经线作为中央经线,则当经度差l等于零时,y=0,同样,在y`=0这个假定下,式(1)为:
x`=f(x)
(3)
假设椭球面某一点的坐标为(△σ,l),其中△σ为这个点的等量纬度σ和投影中心的等量纬度的差数,l为这个点和中央经线的经度差。又设高斯克吕格坐标(x`,y`)和(△σl)的关系为:
x`+iy`=G(△σ+il)
(4)
而兰勃特投影坐标(x,y)和(△σ,l)的关系为:
x+iy=L(△σ+il)
(5)
当l=0,y=y`=0,故:

(6)
由于△σ是地理纬度差△φ的函数,故有:
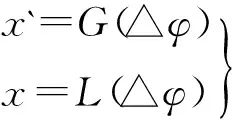
(7)
依x逐级微分式(3),得:

(8)
以上导数必须归算至x=0之上,也就是说,令△σ=0,方能代入式(2)作为系数。根据式(8)即可将各阶导数表示为含高斯投影与兰勃特投影参数的实用公式。根据高斯投影长度变形公式及其中央子午线无变形的特点,并令△φ=0可推导出(过程略):

(9)
由兰勃特投影坐标换算的级数反算公式,并依x逐级微分△φ,令△φ=0,经推导得:

(10)
将式(9)及(10)代入式(8),可得:

(11)
故从兰勃特坐标换算为高斯克吕格坐标的公式为:

(12)
将式中真数与虚数分开,则得换算公式为:
(13)
式(13)左边高斯克吕格投影的坐标原点在中央经线上,x`是从兰勃特投影的中央纬线的纬度φ0起算,所以,必须加入由赤道至纬度φ0的经线长度X0,方能得到高斯克吕格投影上的纵坐标。
对于1975年国际椭球,子午线弧长X0计算式为[9]:
X0=111133.005B0-16038.528sin2B+16.833sin4B-0.022sin6B
反算公式,即从高斯克吕格坐标换算成兰勃特投影的坐标公式可以将公式倒转求之得:

(14)
式中x`同样是从兰勃特投影的中央纬线的纬度φ0起算的,所以,x`由高斯克吕格坐标减去由赤道至纬度φ0的经线长度X0得到。
以上各参数含义及计算式同大地测量学中规定。
2 正解析坐标变换精度分析
当两种地图投影采用同一中央子午线时,采用正解析法与反解析法对同一坐标点的转换结果理论上是相同的,由于反解析法坐标转换结果无误差,而正解析法坐标转换结果随阶数展开存在一定偏差,故两种坐标转换结果之差即可理解为正解析法坐标转换精度。我国国家高斯坐标系通常采用6°带,兰勃特坐标系采用4°带,同时考虑到切兰勃特投影采用平均纬度作为y轴,因此选取2°×6°方格网为单位,以在75椭球下的转换为例,研究正解析法坐标转换精度。

图1 △x变化示意图

图2 △y变化示意图

纬差/(°)△x/10-3m-3.0°-2.0°-1.0°0°1.0°2.0°3.0°0-0.289-0.025-0.00040-0.0004-0.025-0.2890.25-0.1380.0680.0830.0820.0830.068-0.1380.50.0840.1740.1670.1660.1670.1740.0840.750.3570.2850.2500.2490.2500.2850.3571.00.6470.3890.3290.3330.3290.3890.6471.250.9180.4720.4020.4200.4020.4720.9181.51.1230.5160.4690.5130.4690.5161.1231.751.2130.5060.5300.6180.5300.5061.2132.01.1360.4240.5880.7460.5880.4241.136

表2 不同经差和纬差处的△y
由表1、表2中可得:正解析法坐标转换精度绝对值随着点位偏离兰勃特坐标原点越远呈增大趋势,在最大处(x,y)的误差约为0.001 m,可以满足测量和地图制图所要求的精度。
3 结论
本文通过对高斯投影与兰勃特投影正解析坐标转换公式进行重新推导,得出以下主要结论:
(1)通过等角投影与复变函数的内在联系关系,推导得出兰勃特投影与高斯投影的直接换算公式。该公式所含参数少,易于编程计算,成功解决反解析法过程复杂计算量大的问题。
(2)新的解析转换公式在4°(纬差)6°(经差)的转换区域精度达到1 mm,较之前的转换公式精度提高两个数量级,能够满足高精度工程建设的需要。
[1]孙达,蒲英霞. 地图投影[M]. 南京,南京大学出版社,2007.
[2]杨启和. 地图投影变换理论和应用的研究[J]. 解放军测绘学院学报, 1986(1):108-116.
[3]程阳,复变函数与等角投影[J]. 测绘学报,1985(14):51-60.
[4]王美玲,WGS84椭球下的UTM坐标与Clarke80椭球下的兰勃特坐标转换方法研究[J].中国惯性技术学报,2006(5):36-38.
[5]丁佳波. 关于等角投影解析变换的补充[J]. 测绘学报, 1982(1):46-50.
[6]顾雪峰, 李厚朴, 张蕾. 高斯和兰勃特投影间变换的复变函数表示[J]. 舰船电子工程, 2013(7):34-36.
[7]李厚朴, 王瑞, 边少锋. 复变函数表示的高斯投影非迭代公式[J]. 海洋测绘, 2009(6):17-20.
[8]李厚朴, 边少锋, 李海波. 常用等角投影及其解析变换的复变函数表示[J]. 测绘科学技术学报, 2012(2):109-112.
[9]孔祥元,郭际明,刘宗泉.大地测量学基础[M].武汉:武汉大学出版社,2001.
Research of positive analytical transformation between Gauss projection and Lambert projection
ZHANG Jian-xiong,LI Ya-lei
(SchoolofSurveyingandLandInformationEngineeringHenanPolytechnicUniversity,Jiaozuo454003,China)
Gauss projection and Lambert projection are two equal-angle projections frequently used in China.The coordinate conversion between them is a basic problem in application.To the questions of the complexity of negative analytical transformation method and low precision of positive analytical transformation,we derivate the formula using software Mathematica and find that when the area is limited in four latitude difference and six longitude difference the conversion accuracy can up to 1 mm,which can meet the requirements of surveying and mapping precision.
Gauss projection;Lambert projection;analytical transformation;conversion accuracy
2015-12-21
张健雄(1966—),男,湖南冷水江人,博士,教授。
李亚磊(1991—),男,河南杞县人,硕士研究生。
1674-7046(2016)02-0074-06
10.14140/j.cnki.hncjxb.2016.02.014
P282.2
A

